【算法与数据结构】--算法基础--算法入门
一、什么是算法?
算法是一组有序的操作步骤,用于解决特定问题或执行特定任务。它是一种精确而有限的计算过程,以输入数据作为起点,经过一系列明确定义的步骤,最终产生输出结果。算法可以看作是一种计算机程序的抽象,但更侧重于高度抽象和通用性。算法通常具备以下特征:
- 明确性(Definiteness):算法的每一步都必须非常明确和清晰,不会产生歧义。每一步都能够被精确定义和理解。
- 有限性(Finiteness):算法必须在有限步骤内终止,不能进入无限循环。它不能永远执行下去。
- 输入(Input):算法需要接受输入数据,这些输入数据是解决问题所必需的信息。
- 输出(Output):算法必须产生输出,即问题的解或者所需的结果。
- 有效性(Effectiveness):算法必须能够被执行,而且在合理的时间内产生结果。它不应该是一个无法实际运行的抽象。
- 通用性(Generality):算法可以用于解决一类问题,而不仅仅是一个特定实例。
算法在计算机科学和计算领域中起着至关重要的作用。它们用于解决各种问题,从简单的数学计算到复杂的数据分析和人工智能。算法的效率和优化是计算机科学的核心问题之一,因为不同算法的性能可以在处理大规模数据或解决复杂问题时产生显著差异。
Tip:算法是一种计算过程,用于解决问题或执行任务,它的定义清晰明确,具备明确性、有限性、输入、输出、有效性和通用性等特征。算法在计算机科学和工程中扮演着关键角色,是计算机程序的基础。
二、算法的性能分析
算法的性能分析是评估算法在不同输入情况下的效率和资源使用情况的过程。它是计算机科学中非常重要的一部分,可以帮助我们选择合适的算法来解决问题,优化程序的运行时间和资源利用。性能分析通常涉及以下几个关键方面:
- 时间复杂度(Time Complexity):时间复杂度是用来估计算法执行所需时间的度量。它通常表示为一个函数,关于输入数据规模的增长情况。常见的时间复杂度包括常数时间(O(1))、线性时间(O(n))、对数时间(O(log n))、线性对数时间(O(n log n))和指数时间(O(2^n))等。通过分析算法的时间复杂度,我们可以估算出算法在不同输入规模下的运行时间增长趋势。
- 空间复杂度(Space Complexity):空间复杂度用于估计算法在执行过程中所需的内存空间。与时间复杂度类似,空间复杂度也通常表示为一个函数,关于输入数据规模的增长情况。了解算法的空间复杂度有助于我们在有限的内存资源下进行程序设计和优化。
- 最坏情况和平均情况:在性能分析中,通常会考虑算法的最坏情况和平均情况。最坏情况时间复杂度表示在算法执行的所有可能输入中,最长执行时间所对应的情况。平均情况时间复杂度考虑了在不同输入情况下的执行时间的平均值。通常情况下,我们更关注最坏情况,因为它能够保证算法在任何情况下都有良好的性能。
- 空间-时间权衡:某些算法在时间复杂度和空间复杂度之间存在权衡关系。有时,可以通过使用更多的内存来减少执行时间,或者通过减少内存使用来提高执行速度。性能分析可以帮助我们找到最适合特定应用场景的权衡点。
- 常数因子和低阶项:在性能分析中,通常会忽略时间复杂度公式中的常数因子和低阶项。这是因为这些因子通常在输入规模足够大时不会对算法的总体性能产生显著影响。因此,我们更关注时间复杂度的渐进行为。
- 比较不同算法:性能分析还可以用于比较不同算法在解决同一问题上的效率。通过比较它们的时间和空间复杂度,可以选择最适合特定问题的算法。
性能分析是算法设计和优化的关键步骤之一。它可以帮助开发者选择合适的算法、预测程序的运行时间和内存需求,并优化代码以提高性能。然而,需要注意的是,性能分析通常是一种理论上的估算,实际执行时间可能受到硬件、编程语言和编译器等因素的影响。因此,在实际应用中,通常需要进行实际测试和性能调优以获得准确的性能数据。
三、常见算法的时间复杂度
以下是一些常见算法的时间复杂度,按照从最低到最高的顺序排列:
- 常数时间复杂度 - O(1):
- 常数时间复杂度表示算法的执行时间与输入规模无关,执行时间是一个常数。
- 例如:访问数组元素、执行数学运算。
- 对数时间复杂度 - O(log n):
- 对数时间复杂度通常出现在分治和二分查找算法中。
- 例如:二分查找、某些分治算法。
- 线性时间复杂度 - O(n):
- 线性时间复杂度表示算法的执行时间与输入规模成正比。
- 例如:遍历数组、查找未排序的列表中的元素。
- 线性对数时间复杂度 - O(n log n):
- 线性对数时间复杂度通常出现在排序算法中,如快速排序和归并排序。
- 例如:快速排序、归并排序。
- 平方时间复杂度 - O(n^2):
- 平方时间复杂度表示算法的执行时间与输入规模的平方成正比。
- 例如:简单的嵌套循环遍历二维数组、冒泡排序。
- 立方时间复杂度 - O(n^3):
- 立方时间复杂度表示算法的执行时间与输入规模的立方成正比。
- 例如:三重嵌套循环遍历三维数组。
- 指数时间复杂度 - O(2^n):
- 指数时间复杂度表示算法的执行时间随着输入规模呈指数增长。
- 例如:穷举法解决组合问题。
- 阶乘时间复杂度 - O(n!):
- 阶乘时间复杂度表示算法的执行时间与输入规模的阶乘成正比。
- 例如:解决旅行商问题的穷举法。
Tip:上述时间复杂度仅是一些示例,实际应用中可能还有其他更复杂的时间复杂度。在选择算法时,通常希望选择时间复杂度较低的算法,特别是在处理大规模数据时,以确保程序能够在合理的时间内完成任务。但同时,还需要综合考虑其他因素,如空间复杂度、算法的实现难度和问题的特性等。
四、总结
本文首先介绍了什么是算法,强调了算法的明确性、有限性、输入输出、有效性和通用性等关键特征。接着,探讨了算法的性能分析,包括时间复杂度、空间复杂度、最坏情况和平均情况等方面,以及比较不同算法的方法。最后,列举了一些常见算法的时间复杂度示例,从常数时间到指数时间不等,强调了选择合适的算法以优化程序性能的重要性。性能分析是算法设计和优化的关键,它有助于开发者选择合适的算法、预测程序性能和进行代码优化。
相关文章:

【算法与数据结构】--算法基础--算法入门
一、什么是算法? 算法是一组有序的操作步骤,用于解决特定问题或执行特定任务。它是一种精确而有限的计算过程,以输入数据作为起点,经过一系列明确定义的步骤,最终产生输出结果。算法可以看作是一种计算机程序的抽象&a…...

AnyDesk密钥
最近最新的密钥:7K2CV32ER6T8F8I 这款软件应该是目前用的最好的可以免费的软件了,记录一下密钥...

C#(Csharp)我的基础教程(二)(我的菜鸟教程笔记)-属性和字段的探究与学习
目录 1、字段字段特点:2、属性属性的特点 1、字段 字段是定义在方法外面的变量,是成员变量,主要是为了类的内部数据交换使用,字段一般是用private修饰,也可以用readonly修饰,表示只读字段,其它…...

Programming abstractions in C阅读笔记:p176-p178
《Programming Abstractions In C》学习第59天,p176-p178总结。 一、技术总结 1.addtive sequences tn tn-1 tn-2 序列:3, 7, 10, 17, 27, 44, 71, 115, 186, 301, 487, 788, 1275, … p177, As a general class, the sequences that follow this…...
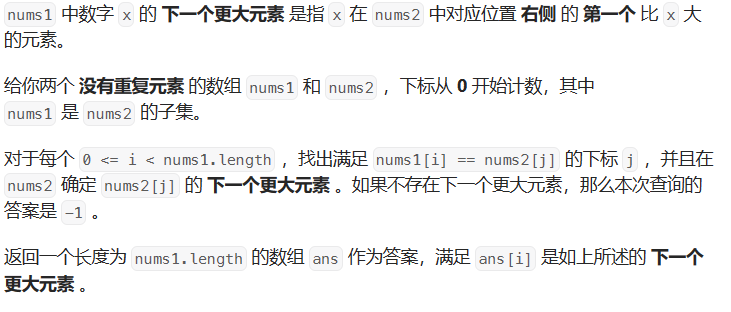
LeetCode-496-下一个更大元素
题目描述: 题目链接:LeetCode-496-下一个更大元素 解题思路: 方法一:暴力 方法二:单调栈 方法一代码实现: class Solution {public int[] nextGreaterElement(int[] nums1, int[] nums2) {// 最笨的方法&am…...

C++中的Lambda表达式
一、为什么要有lambda表达式 struct Goods {string _name; // 名字double _price; // 价格int _evaluate; // 评价Goods(const char* str, double price, int evaluate):_name(str), _price(price), _evaluate(evaluate){} }; 对于一个Goods类,需要对其中3个成员分…...

dockerfile搭建lnmp
systemctl stop firewalld systemctl disable firewalld setenforce 0 docker network create --subnet172.18.0.0/16 --opt "com.docker.network.bridge.name""docker1" mynetwork #部署nginx(容器IP 为 172.18.0.10) mkdir /…...

python之数据库操作详解
一般来说,我们对数据库里的操作需要先连接,创建游标对象,然后通过游标对象执行SQL语句去对SQL的数据进行操作,本篇文章旨在记录与科普。 1.cursor相关 元组是不可变的数据类型,只能查询,不能修改…...

完成flex布局与float布局
一、flex布局 <style>.nav {display: flex;background-color: #f8f8f8; /* 导航栏背景颜色 */}.nav a {flex: 1;display: flex;align-items: center;justify-content: center;padding: 14px 16px;text-decoration: none;color: #555555; /* 导航栏文字颜色 */}.nav a:ho…...
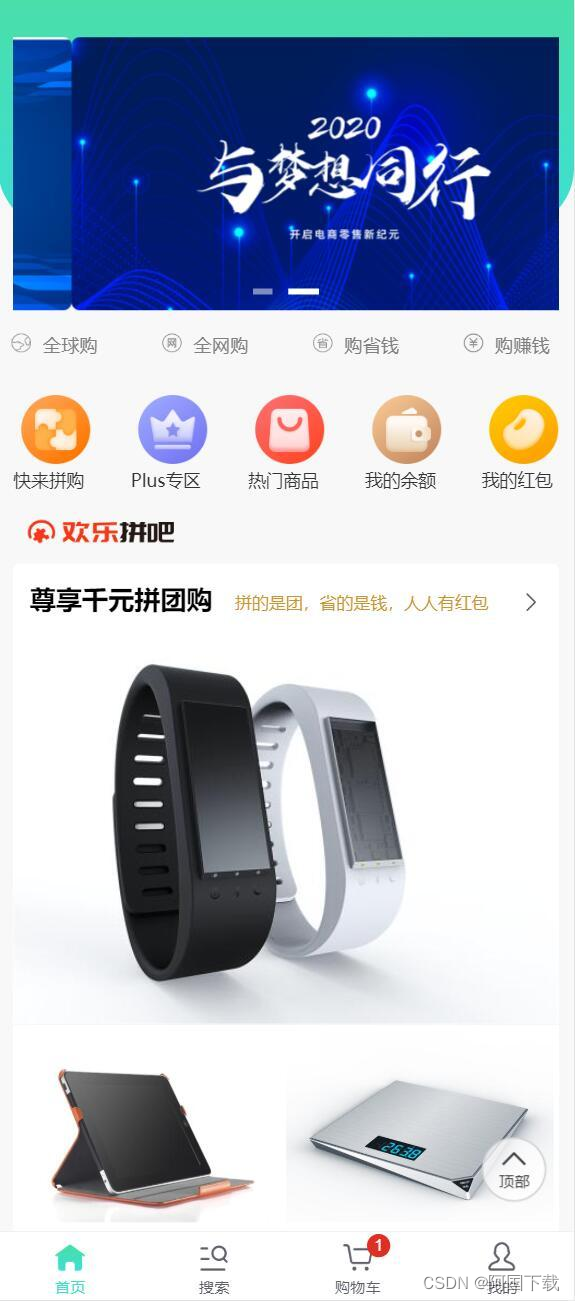
ThinkPHP团购拼购商城源码/带分销团购商城网站源码/完美版
ThinkPHP团购拼购商城源码,带分销团购商城网站源码,很完美的一套基于ThinkPHP开发的团购分销商城源码,界面也很大气,站长亲测。有需要的可以借鉴一下。 下载地址:https://bbs.csdn.net/topics/613231434...

awvs 中低危漏洞
低危 X-Frame-Options Header未配置 查看请求头中是否存在X-Frame-Options Header字段 会话Cookie中缺少secure属性(未设置安全标志的Cookie) 当cookie设置为Secure标志时,它指示浏览器只能通过安全SSL/TLS通道访问cookie。 未设置HttpOnly标志的Cookie 当cookie设置…...

openGauss学习笔记-95 openGauss 数据库管理-访问外部数据库-postgres_fdw
文章目录 openGauss学习笔记-95 openGauss 数据库管理-访问外部数据库-postgres_fdw95.1 使用postgres_fdw95.2 postgres_fdw下推主要成分95.3 常见问题95.4 注意事项 openGauss学习笔记-95 openGauss 数据库管理-访问外部数据库-postgres_fdw openGauss的fdw实现的功能是各个…...

并不止于表面理论和简单示例——《Python数据科学项目实战》
Python 现在可以说是运用最广泛的编程语言之一,使用 Python 的人不只局限在计算机相关专业的从业者,很多来自金融领域、医疗领域以及其他我们无法想象的领域的人,每天都在使用 Python处理各种数据、使用机器学习进行预测以及完成各种有趣的工作。 长久以来ÿ…...
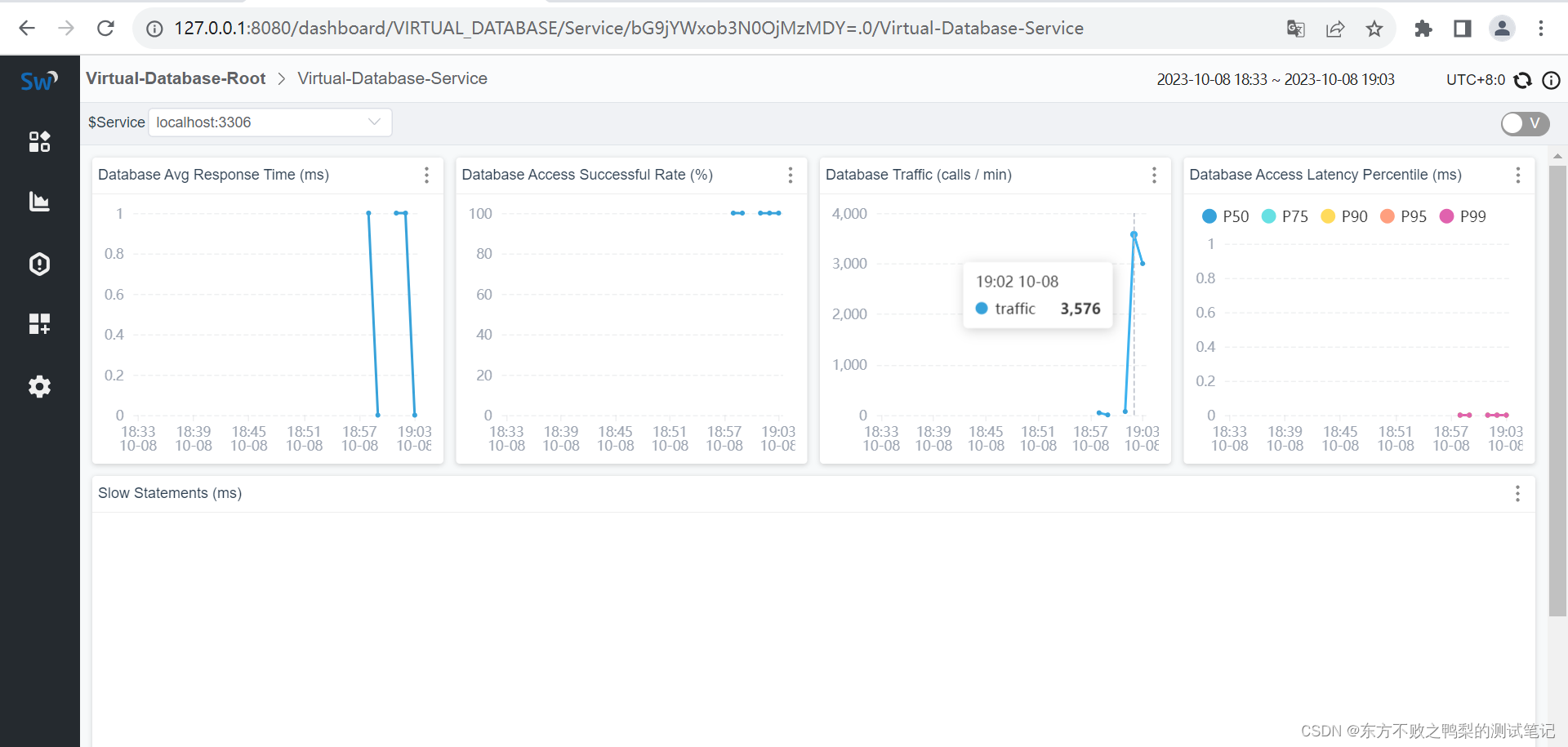
skywalking功能介绍
目标 前置:性能监控-微服务链路追踪skywalking搭建-CSDN博客 使用skywalking进行链路监控,找到应用的时间消耗再哪。 服务 服务信息 请求接口后查看skywalking,可以看到有一个请求,响应时间为1852ms,性能指数Apdex…...
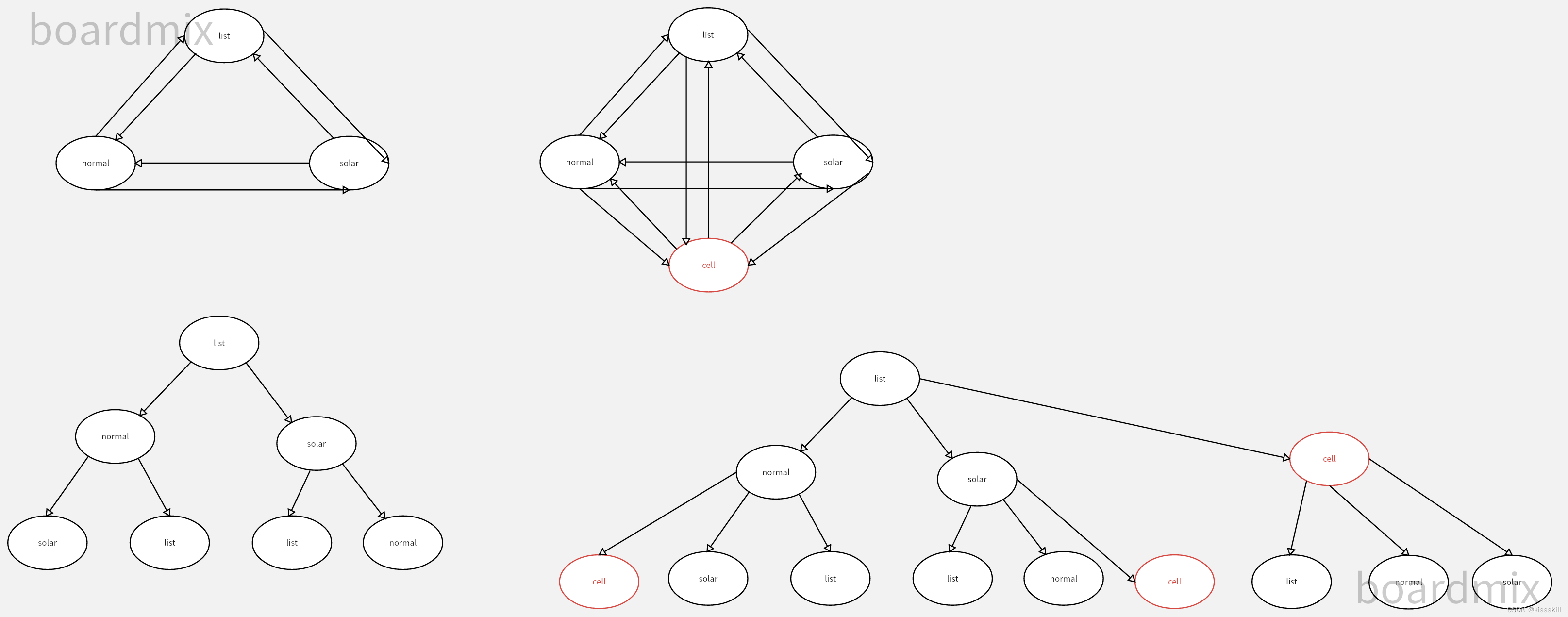
c++桥接模式,中介者模式应用实现状态跳转
上图为例,按上述两种方式实现的模式跳转,如果在原先的三种模式之间再增加多一种模式,就会引起每个模式都会要求改变,并且逻辑混乱,因此更改模式为桥接中介者访问,将抽象和实现分离,实现之间采用…...
【SpringCloud】Ribbon负载均衡原理、负载均衡策略、饥饿加载
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 Redis 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 Ribbon 一、 Ribbon负载均衡原理1.1 负载均…...

亘古难题——前端开发or后端开发
一、引言 前端开发 前端开发是创建WEB页面或APP等前端界面呈现给用户的过程,通过HTML,CSS及JavaScript以及衍生出来的各种技术、框架、解决方案,来实现互联网产品的用户界面交互。 前端开发从网页制作演变而来,名称上有很明显的时…...

Notepad++提取含有特定字符串的行
ctrl M快捷键,进入"标记" 页面 标记所在行–循环查找-- 正则表达式 – 输入关键字 – 全部标记 – Copy Marked Text 关键字格式如下: .*关键字.*ctrl v,粘贴即可。...

host配置
配置host文件的作用主要是用于自定义域名与IP地址之间的映射关系。Host文件是一个操作系统用于将人类可读的域名(例如:www.example.com)映射到IP地址(例如:192.168.1.1)的文件。当你在浏览器中输入一个网址…...

```,```中间添加 # + 空格 + 空行后遇到的底部空行出错,书接上回,处理空行
【python查找替换:查找空行,空行前后添加,中间添加 # 空格 空行后遇到的第1行文字? - CSDN App】http://t.csdnimg.cn/QiKCV def is_blank(line):return len(line.strip()) 0txt 时间戳: ("%Y-%m-%d %H:%M:…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
