【YBT2023寒假Day14 C】字符串题(SAM)(树链剖分)(线段树)
字符串题
题目链接:YBT2023寒假Day14 C
题目大意
对于一个字符串 S 定义 F(S) 是 fail 树上除了 0 点其它点的深度和。
G(S) 是 S 每个子串 S’ 的 F(S’) 之和。
然后一个空串,每次在后面加一个字符,要你维护这个串的 G 值。
思路
考虑把 G(S[1,x])G(S[1,x])G(S[1,x]) 值差分一下,会发现 G(S[1,i])−G(S[1,i−1])G(S[1,i])-G(S[1,i-1])G(S[1,i])−G(S[1,i−1]) 的值其实是以 iii 为结尾的子串的 FFF 值之和。
那从子串变成了一个后缀,看起来就可做很多了,考虑怎么算。
那我们看 fail 树性质,一个字符串 SSS 中 jjj 是 iii 的祖先当且仅当 S[1,j]=S[i−j+1,i]S[1,j]=S[i-j+1,i]S[1,j]=S[i−j+1,i]。
那 F(S)F(S)F(S) 就是满足 S[1,j]=S[i−j+1]S[1,j]=S[i-j+1]S[1,j]=S[i−j+1] 且 1⩽j<i1\leqslant j<i1⩽j<i 的 (i,j)(i,j)(i,j) 对数。
那也就是在 SSS 里面选一个前缀,再选一个非前缀,它们相等的方案数。
注意到我们要求的是以 iii 结尾的 FFF 值之和,那开头就不固定,结尾是固定的。
那 FFF 值是选一个前缀,再一个非前缀,那这个是开头固定,结尾不固定。
那你这个开头固定放在开头不固定里,它不固定了,你这个结尾不固定在结尾固定里面肯定也是不固定。
所以头尾都不固定,只需要两个不是同一个位置的字符串相等即可。
那答案就是所有本质不同的子串的出现次数 xxx 的 (x2)\binom{x}{2}(2x) 之和。
那注意到不需要在线,我们可以先建出最后的后缀树。
那我们用一个 dxd_xdx 表示每个点 xxx 对于子串的出现次数。
那插入就是把它到祖先路径的 dxd_xdx 加一,询问就是所有点的 endpos 大小乘 (dx2)\binom{d_x}{2}(2dx)。
那这个维护这个和不难,我们记录着这个和 sumsumsum,每次要插入的时候,每个新贡献的值就是它 endpos 集合大小乘上 dxd_xdx(这个 dxd_xdx 还没加 111),然后你再把 dxd_xdx 加一。
那这个是路径加值,路径求和,直接树链剖分线段树维护即可。
复杂度 O(nlog2n)O(n\log ^2n)O(nlog2n)
ex:
如果强制在线,我们也可以用 LCT 来维护这棵树,那就也是同样的操作,复杂度 O(nlogn)O(n\log n)O(nlogn)。
代码
#include<cstdio>
#include<vector>
#define ll long long
#define mo 1000000007using namespace std;const ll N = 4e5 + 100;
ll n, fa[N], sz[N], son[N], dfn[N], top[N], dy[N];
ll lst = 1, tot = 1, pla[N];
char s[N];struct node {ll son[26], len, fa;
}d[N];struct XD_tree {ll num[N << 2], f[N << 2], lzy[N << 2];void up(ll now) {num[now] = (num[now << 1] + num[now << 1 | 1]) % mo;f[now] = (f[now << 1] + f[now << 1 | 1]) % mo;}void downa(ll now, ll x) {(f[now] += x * num[now] % mo) %= mo;(lzy[now] += x) %= mo;}void down(ll now) {if (lzy[now]) {downa(now << 1, lzy[now]); downa(now << 1 | 1, lzy[now]);lzy[now] = 0;}}void build(ll now, ll l, ll r) {if (l == r) {num[now] = d[dy[l]].len - d[d[dy[l]].fa].len;return ;}ll mid = (l + r) >> 1;build(now << 1, l, mid); build(now << 1 | 1, mid + 1, r);up(now);}void update(ll now, ll l, ll r, ll L, ll R, ll x) {if (L <= l && r <= R) {downa(now, x); return ;}ll mid = (l + r) >> 1; down(now);if (L <= mid) update(now << 1, l, mid, L, R, x);if (mid < R) update(now << 1 | 1, mid + 1, r, L, R, x);up(now);}ll query(ll now, ll l, ll r, ll L, ll R) {if (L <= l && r <= R) return f[now];ll mid = (l + r) >> 1; down(now); ll re = 0;if (L <= mid) (re += query(now << 1, l, mid, L, R)) %= mo;if (mid < R) (re += query(now << 1 | 1, mid + 1, r, L, R)) %= mo;return re;}
}T;struct SLPF {vector <ll> G[N];void add(ll x, ll y) {G[x].push_back(y);}void dfs0(ll now, ll father) {fa[now] = father; sz[now] = 1;for (ll i = 0; i < G[now].size(); i++) {ll x = G[now][i];dfs0(x, now); sz[now] += sz[x];if (sz[x] > sz[son[now]]) son[now] = x;}}void dfs1(ll now, ll father) {dfn[now] = ++dfn[0]; dy[dfn[0]] = now;if (son[now]) {top[son[now]] = top[now]; dfs1(son[now], now);}for (ll i = 0; i < G[now].size(); i++) {ll x = G[now][i]; if (x == son[now]) continue;top[x] = x; dfs1(x, now);}}void build() {dfs0(1, 0); top[1] = 1; dfs1(1, 0);T.build(1, 1, tot);}void update_root(ll now) {while (now) {T.update(1, 1, tot, dfn[top[now]], dfn[now], 1);now = fa[top[now]];}}ll query_root(ll now) {ll re = 0;while (now) {(re += T.query(1, 1, tot, dfn[top[now]], dfn[now])) %= mo;now = fa[top[now]];}return re;}
}P;struct SAM {ll insert(ll x) {ll p = lst, np = ++tot; lst = np;d[np].len = d[p].len + 1;for (; p && !d[p].son[x]; p = d[p].fa) d[p].son[x] = np;if (!p) d[np].fa = 1;else {ll q = d[p].son[x];if (d[q].len == d[p].len + 1) d[np].fa = q;else {ll nq = ++tot; d[nq] = d[q];d[nq].len = d[p].len + 1;d[q].fa = d[np].fa = nq;for (; p && d[p].son[x] == q; p = d[p].fa) d[p].son[x] = nq;}}return np;}void build() {for (ll i = 2; i <= tot; i++) P.add(d[i].fa, i);}
}S;int main() {freopen("string.in", "r", stdin);freopen("string.out", "w", stdout);scanf("%lld", &n);scanf("%s", s + 1);for (ll i = 1; i <= n; i++) pla[i] = S.insert(s[i] - 'a');S.build(); P.build();ll sum = 0, ans = 0;for (ll i = 1; i <= n; i++) {(sum += P.query_root(pla[i])) %= mo;P.update_root(pla[i]);(ans += sum) %= mo;printf("%lld\n", ans);}return 0;
}
相关文章:
(树链剖分)(线段树))
【YBT2023寒假Day14 C】字符串题(SAM)(树链剖分)(线段树)
字符串题 题目链接:YBT2023寒假Day14 C 题目大意 对于一个字符串 S 定义 F(S) 是 fail 树上除了 0 点其它点的深度和。 G(S) 是 S 每个子串 S’ 的 F(S’) 之和。 然后一个空串,每次在后面加一个字符,要你维护这个串的 G 值。 思路 考虑…...

Tailwind CSS 在Vue中的使用
什么是Tailwind CSS? Tailwind CSS 是一个功能类优先的 CSS 框架,它集成了诸如 flex, pt-4, text-center 和 rotate-90 这样的的类,支持 hover 和 focus 样式,它们能直接在脚本标记语言中组合起来,构建出任何设计。 …...
)
三层楼100人办公网络如何规划设计实施(实战案例)
如何设计组网 1.采用防火墙+三层交换机+二层POE交换机+AP的方案 2.三层交换机作为网络的核心,提供网络的配置、划分和各个VLAN间的数据交换,而每个VLAN由二层交换机组建 3.网络主干设备的选型,建议网络主干设备或核心层设备选择具备第3层交换功能的高性能主干交换机。 4…...
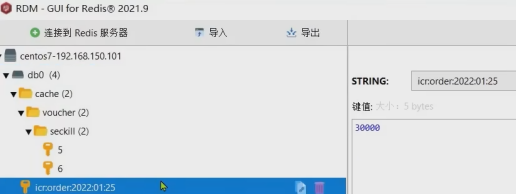
Redis:实现全局唯一ID
Redis:实现全局唯一ID一. 概述二. 实现(1)获取初始时间戳(2)生成全局ID三. 测试为什么可以实现全局唯一?其他唯一ID策略补充:countDownLatch一. 概述 全局ID生成器:是一种在【分布式…...

webpack打包基本原理——实现webpack打包核心功能
webpack打包的基本原理 核心功能就是把我们写的模块化代码转换成浏览器能够识别运行的代码,话不多说我们一起来了解它 首先我们建一个空项目用 npm init -y 创建一个初始化的,在跟目录下创建src文件夹,src下创建index.js,add.js…...
git的使用(终端输入指令) 上
git目录前言1.创建仓库2.创建文件和修改数据状态分区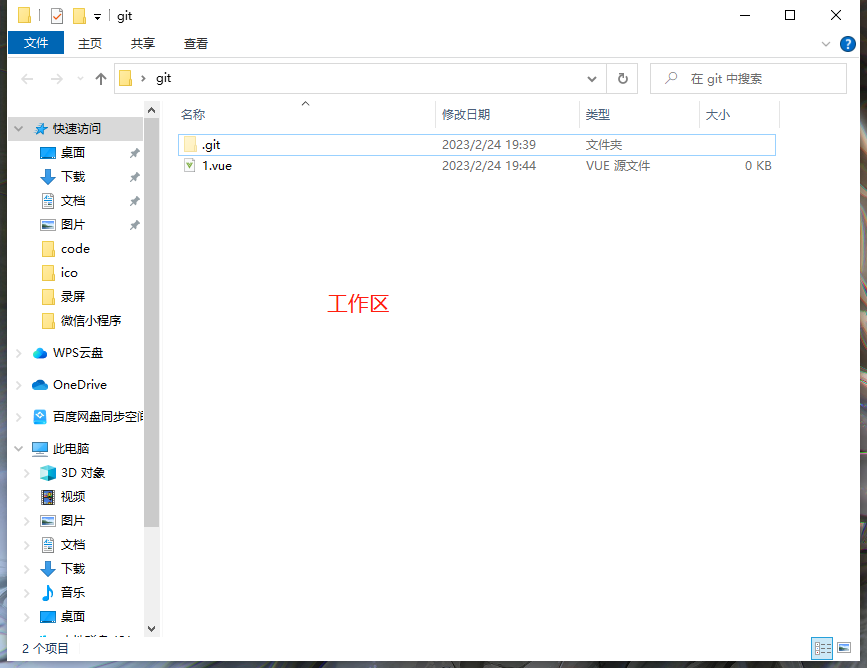3 .删除、撤销重置 、和比较前言 今天带大家手把手敲一遍 git 流程: 安装一下git(详细观看我之前发的git文档࿰…...

react定义css样式,使用less,css模块化
引入外部 css文件 import ./index.css此时引入的样式是全局样式 使用less 安装 npm i style-loader css-loader sass-loader node-sass -D生成config文件夹 npm run eject配置 以上代码运行完,会在根目录生成config文件夹 进入 config > webpack.config.js 查找…...

基于JavaWeb的学生管理系统
文章目录 项目介绍主要功能截图:登录用户信息管理院系信息管理班级信息管理新增学生课程管理成绩管理部分代码展示设计总结项目获取方式🍅 作者主页:Java韩立 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系�…...
win11右键新建菜单添加选项
需要操作 2 处注册表, 以下以在右键新建菜单中添加 .html 为例 在主键 HKEY_CLASSES_ROOT 中,搜索 .html 找到后 ,右键点击它,选 新建 ->项, 在这里插入图片描述 项目名字是:ShellNew 新建后&#x…...
)
leetcode Day5(卡线复试,放弃版)
Day5 最后一个单词长度(要求最后一个,可以反向计数) int lens.length()-1; while(s.charAt(len)){len--;//最后是一个空格,就是无字符时 } int wordlen0;//记录字符长度 /*charAt() 方法用于返回指定索引处的字符。索引范围为从 0…...
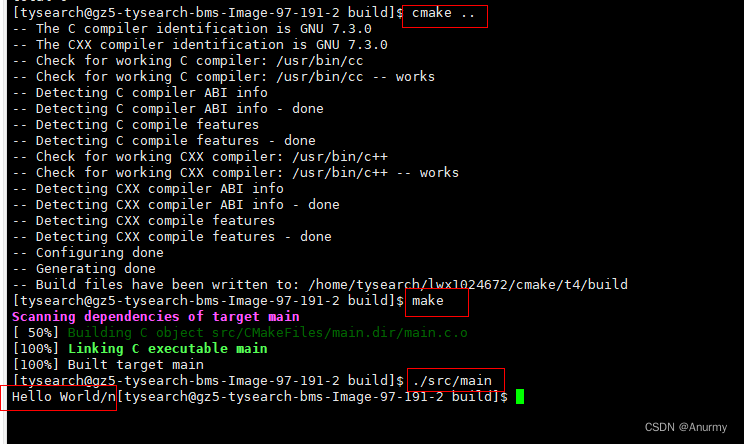
cmake 入门二 库的编译,安装与使用
工程描述 1,建立一个静态库和动态库,提供HelloFunc 函数供其他程序编程使用,HelloFunc 向终端输出Hello World字符串。 2,安装头文件与共享库。 1 库的工程结构 1.1 工程目录下的CMakeLists.txt PROJECT…...

Python中实现将内容进行base64编码与解码
一、需求说明需要使用Python实现将内容转为base64编码,解码,方便后续的数据操作。二、base64简介Base64是一种二进制到文本的编码方式【是一种基于 64 个可打印字符来表示二进制数据的表示方法(由于 2^664,所以每 6 个比特为一个单…...

集合TreeSet的使用-java
TreeSet的特点:可排序、不重复、无索引。可排序:按照元素的大小默认升序排序;底层是基于红黑树的数据结构实现排序的,增删改查性能都较好。对于数值、字符串类型的(Integer 、Double、String)TreeSet可以排…...

Mybatis-plus 分页集成以及基本使用总结 入门和案例 注解连表查询分页案例等
简介 Mybaits-plus 是mybits 的升级版,从mybaits 升级到mybaits-plus 可以实现平滑升级 Mybaits-plus 本身提供了大量的基本查询方法以及强大的 Wrapper(包装) 类 用于查询的 QueryWrapper 以及 更新的 UpdateWrapper ,使用Wrapper 基本已经可以构建大…...

5个设计师常用素材库
推荐5个设计素材网站,免费下载! 1、菜鸟图库 菜鸟图库-免费设计素材下载 菜鸟图库是一个素材量非常丰富的网站,该网站聚合了平面、UI、淘宝电商、高清背景图、图片、插画等高质量素材。平面设计模板非常多,很多都能免费下载&…...
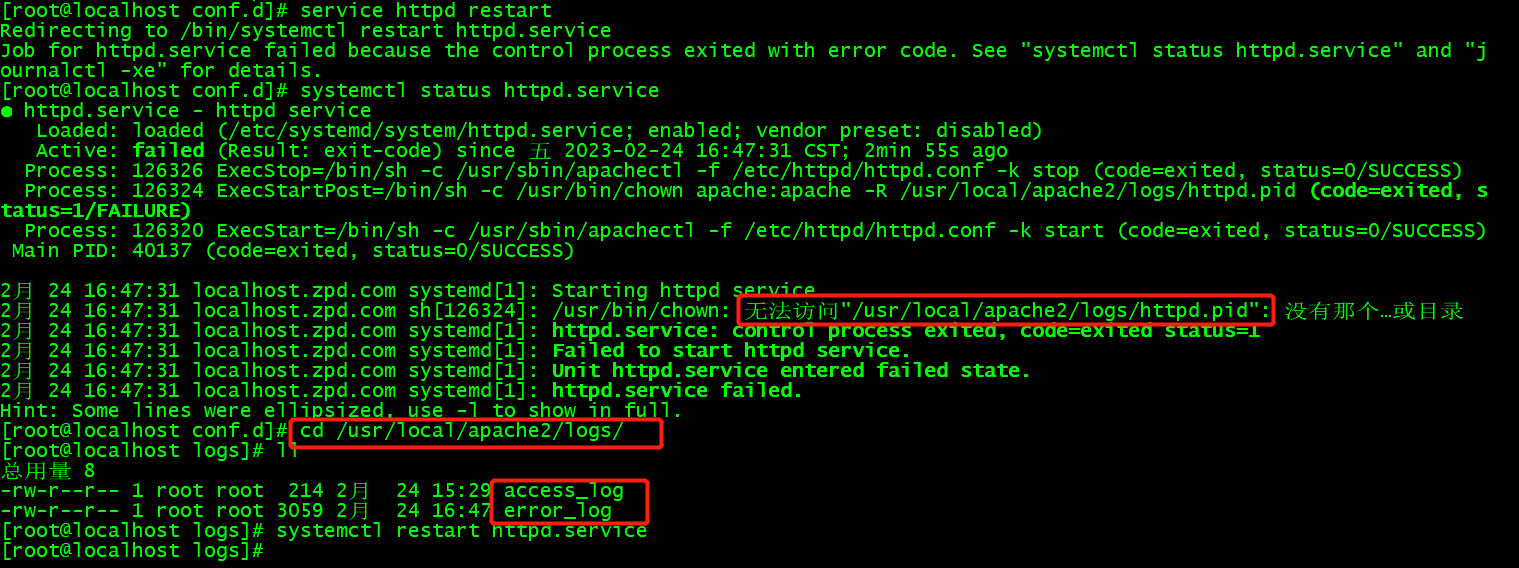
PHP/7.2.11 缺少 apache2/logs/httpd.pid 文件
启动服务时:systemctl restart httpd.service,报错:● httpd.service - httpd serviceLoaded: loaded (/etc/systemd/system/httpd.service; enabled; vendor preset: disabled)Active: failed (Result: exit-code) since 五 2023-02-24 16:1…...

【centos7下部署mongodb】
一.安装环境 CentOS7MongoDB4.0.13正式版。 二.下载MongoDB 1.1 官网下载地址:https://fastdl.mongodb.org/linux/mongodb-linux-x86_64-4.0.13.tgz 1.2 将压缩包通过xftp上传到服务器/opt目录,然后解压、改名 三. 配置环境变量及配置文件 3.1配置系…...
)
pycharm首次使用爬虫框架scrapy遇到的问题和解决方法(二)
在首次使用scrapy框架的过程中,一直是对着别人的框架步骤撸代码的。然而,撸着撸着发现好像别人的也用不了。后面就只能自己找踏坑了。 问题报错: 1,IndexError: list index out of range 2,pymysql.err.ProgrammingError: (1064, "You have an error in your SQL s…...
:table_apisql)
pyflink学习笔记(二):table_apisql
Joins Inner Join 官网说明:和 SQL 的 JOIN 子句类似。关联两张表。两张表必须有不同的字段名,并且必须通过 join 算子或者使用 where 或 filter 算子定义至少一个 join 等式连接谓词。先创建2个表,两个表的字段是相同的,我想验证…...
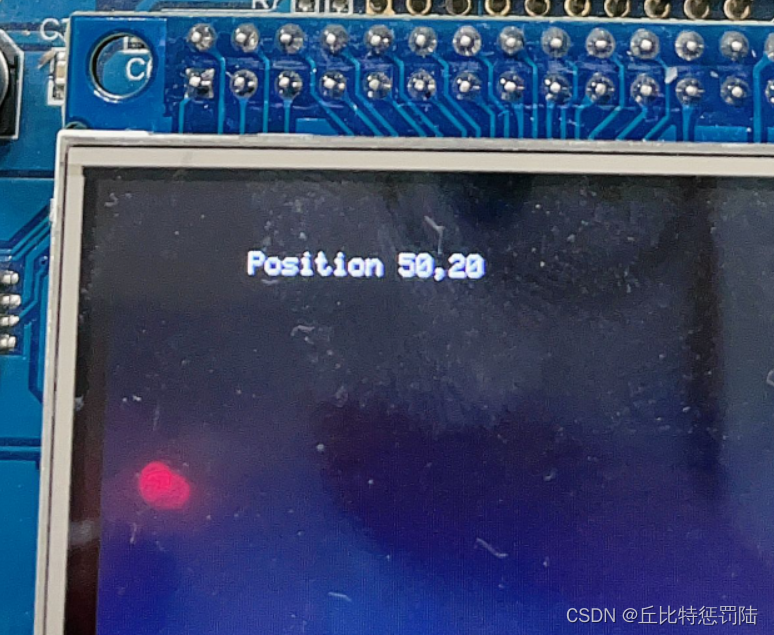
嵌入式 STM32 实现STemwin移植+修改其配置文件,驱动LCD显示文本 (含源码,建议收藏)
目录 一、STemwin 简介 二、源码下载 1、在移植STemwin源码之前,需要一个已经具备LCD读写,填充指定颜色等函数功能的一个工程; 2、STemwin 3、源码下载 三、STemwin移植 1、解压源码路径 2、STemwin文件介绍 四、修改配置文件&…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
