当前位置： 首页 > news >正文

常用傅里叶变换表

news 2025/7/3 13:32:40
  • 傅里叶展开

f(x)=\frac{a_0}{2}+\sum_{k=1}^\infty a_kcoskx+b_ksinkx

\left\{\begin{matrix} a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx\\ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)cosnxdx\\ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)sinnxdx \end{matrix}\right.

  • 傅里叶变换

F(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}f(x)e^{-ikx}dx

  • 傅里叶逆变换

f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}F(k)e^{ikx}dk

  • 时域信号

g(t)\equiv \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}G(\omega)e^{i\omega t}d\omega

  • 弧频域信号

G(f)=\int_{-\infty}^{+\infty}g(t)e^{-i2\pi ft}dt

  • 线性变换

a\cdot g(t)+b\cdot h(t)\rightarrow a\cdot G(f)+b\cdot H(f)

  • 时域平移

g(t-a)\rightarrow e^{-i2\pi af}G(f)

  • 频域平移

e^{iat}\rightarrow G(f-\frac{a}{2\pi})

  • 伸缩变换

g(at)\rightarrow\frac{1}{|a|}G(\frac{f}{a})

  • 微分性质

\frac{d^n}{dt^n}g(t)\rightarrow (i2\pi f)^nG(f)

  • 逆变换的微分性质

t^ng(t)\rightarrow (\frac{i}{2\pi})^n\frac{d^n}{df^n}G(f)

  • 卷积定理

(g*h)(t)\rightarrow G(f)H(f)

原函数变换结果
e^{iat}\delta(f-\frac{a}{2\pi})
e^{-at^2}\sqrt{\frac{\pi}{a}}\cdot e^{-\frac{(\pi f)^2}{a}}
cos(at)\frac{\delta(f-\frac{a}{2\pi})+\delta(f+\frac{a}{2\pi})}{2}
cos(at^2)\sqrt{\frac{\pi}{a}}cos(\frac{\pi^2f^2}{a}-\frac{\pi}{4})
sin(at)\frac{\delta(f-\frac{a}{2\pi})-\delta(f+\frac{a}{2\pi})}{2i}
sin(at^2)-\sqrt{\frac{\pi}{a}}sin(\frac{\pi^2f^2}{a}-\frac{\pi}{4})
e^{-a|t|}(a>0)\frac{2a}{a^2+4\pi^2f^2}
\frac{1}{\sqrt{|t|}}\frac{1}{\sqrt{|f|}}
1\delta(f)
\delta(t)1
t^n(\frac{i}{2\pi})^n\delta^{(n)}(f)
\frac{1}{t}-i\pi\cdot sgn(f)
\frac{1}{t^n}-i\pi\cdot \frac{(-i2\pi f)^{n-1}}{(n-1)!}\cdot sgn(f)
sgn(t)\frac{1}{i\pi f}
u(t)\frac{1}{2}(\frac{1}{i\pi f}+\delta(f))
e^{-at}u(t)\frac{1}{a+i2\pi f}
rect(at)\frac{1}{|a|}\cdot sinc(\frac{f}{a})
sinc(at)\frac{1}{|a|}\cdot rect(\frac{f}{a})

  • 单位阶跃函数：u(t) 
  • 符号函数：

sgn(x)=\left\{\begin{matrix} 1&x>0\\ 0&x=0\\ -1&x<0 \end{matrix}\right.

  • 矩形函数：

rect=\left\{\begin{matrix} 1 & |x|<\frac{1}{2}\\ 0 & others \end{matrix}\right.

  • 辛格函数：

sinc(x)=\frac{sin(\pi x)}{\pi x}

相关文章：

常用傅里叶变换表

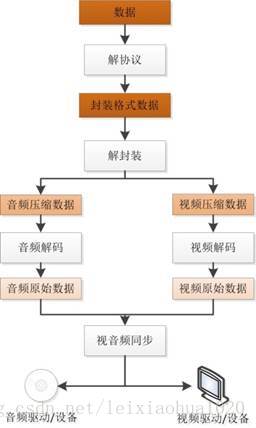
傅里叶展开 傅里叶变换 傅里叶逆变换 时域信号 弧频域信号 线性变换 时域平移 频域平移 伸缩变换 微分性质 逆变换的微分性质 卷积定理 原函数变换结果 单位阶跃函数&#xff1a; 符号函数&#xff1a; 矩形函数&#xff1a; 辛格函数&#xff1a;...

编程日记 2023/10/15 9:52:25

生活中的视音频技术

生活中的视音频技术 平时我们打开电脑中自己存电影的目录的话&#xff0c;一般都会如下图所示&#xff0c;一大堆五花八门的电影。&#xff08;其实专业的影视爱好者一概会把影视文件分门别类的&#xff0c;但我比较懒&#xff0c;一股脑把电影放在了一起&#xff09; 因为下载…...

编程日记 2023/10/15 9:51:24

一种用于肽图分析的烷化剂，Desthiobiotin-Iodoacetamide

中文名&#xff1a;脱硫生物素-碘乙酰胺 英文名&#xff1a;Desthiobiotin-Iodoacetamide 化学式&#xff1a;C14H25IN4O3 分子量&#xff1a;424.28 外观&#xff1a;固体/粉末 规格&#xff1a;10mg、25mg、50mg等&#xff08;接受各种规格的定制服务&#xff0c;具体可…...

编程日记 2023/10/15 9:50:23

【(数据结构) —— 顺序表的应用-通讯录的实现】

&#xff08;数据结构&#xff09;—— 顺序表的应用-通讯录的实现 一.通讯录的功能介绍1.基于动态顺序表实现通讯录(1). 功能要求(2).重要思考 二. 通讯录的代码实现1.通讯录的底层结构(顺序表)(1)思路展示(2)底层代码实现(顺序表&#xff09; 2.通讯录上层代码实现(通讯录结构…...

编程日记 2023/10/15 9:49:21

macbook磁盘清理免费教程分享

笔记本电脑在是我们工作和生活中重要组成部分&#xff0c;磁盘清理是常有的事&#xff0c;而macbook作为其中的代表之一&#xff0c;也越来越受到人们的青睐。然而&#xff0c;如何进行macbook磁盘清理&#xff0c;也事许多人都会遇到的问题&#xff0c;特别是被提示“磁盘已满…...

编程日记 2023/10/15 9:48:20

cartographer_ros数据加载与处理

node_main.cc 坐标系的读取通过tf_bufferautonode类是cartographer_ros接收传感器数据&#xff0c;并传输到cartographer里&#xff0c;同时还会发布map&#xff0c;轨迹等node_options数据传给两个地方&#xff0c;一个是map_builder进行slam操作&#xff0c;一个是node做数据…...

编程日记 2023/10/15 9:47:19

设计模式-7种结构型模式

适配器模式&#xff1a; 将一个类的接口转换成用户希望得到的另一种接口。它使原本不相容的接口得以协同调用。 桥接模式&#xff1a; 将类的抽象部分和他的实现部分分离开来。是他们可以独立的变化。 它是用组合关系代替继承关系来实现&#xff0c;从而降低了抽象和实现这两…...

编程日记 2023/10/15 9:45:17

华为李鹏：加速5G商业正循环，拥抱更繁荣的5.5G（5G-A）

2023年10月10日&#xff0c;在华为主办的第十四届全球移动宽带论坛上&#xff0c;华为高级副总裁、运营商BG总裁李鹏面向来自全球的运营商和产业伙伴&#xff0c;提出抓住网络需求和趋势的力量——“面向后天的业务&#xff0c;积极规划明天的网络&#xff0c;加速5G商业正循环…...

编程日记 2023/10/15 9:44:15

Marin说PCB之CoilcraftBourns POC 电感的性能对比

十一小长假本来是一件美好事情。可是天有不测风云&#xff0c;小编我却有祸兮来了。本来是公司的硬件同事强哥要回以色列了&#xff0c;最近他们国家那边都在打仗&#xff0c;强哥本着舍身为国的精神回国抗战去了。小编我就想着在他回国之前搞了篮球比赛送别一下他呢&#xff0…...

编程日记 2023/10/15 9:43:12

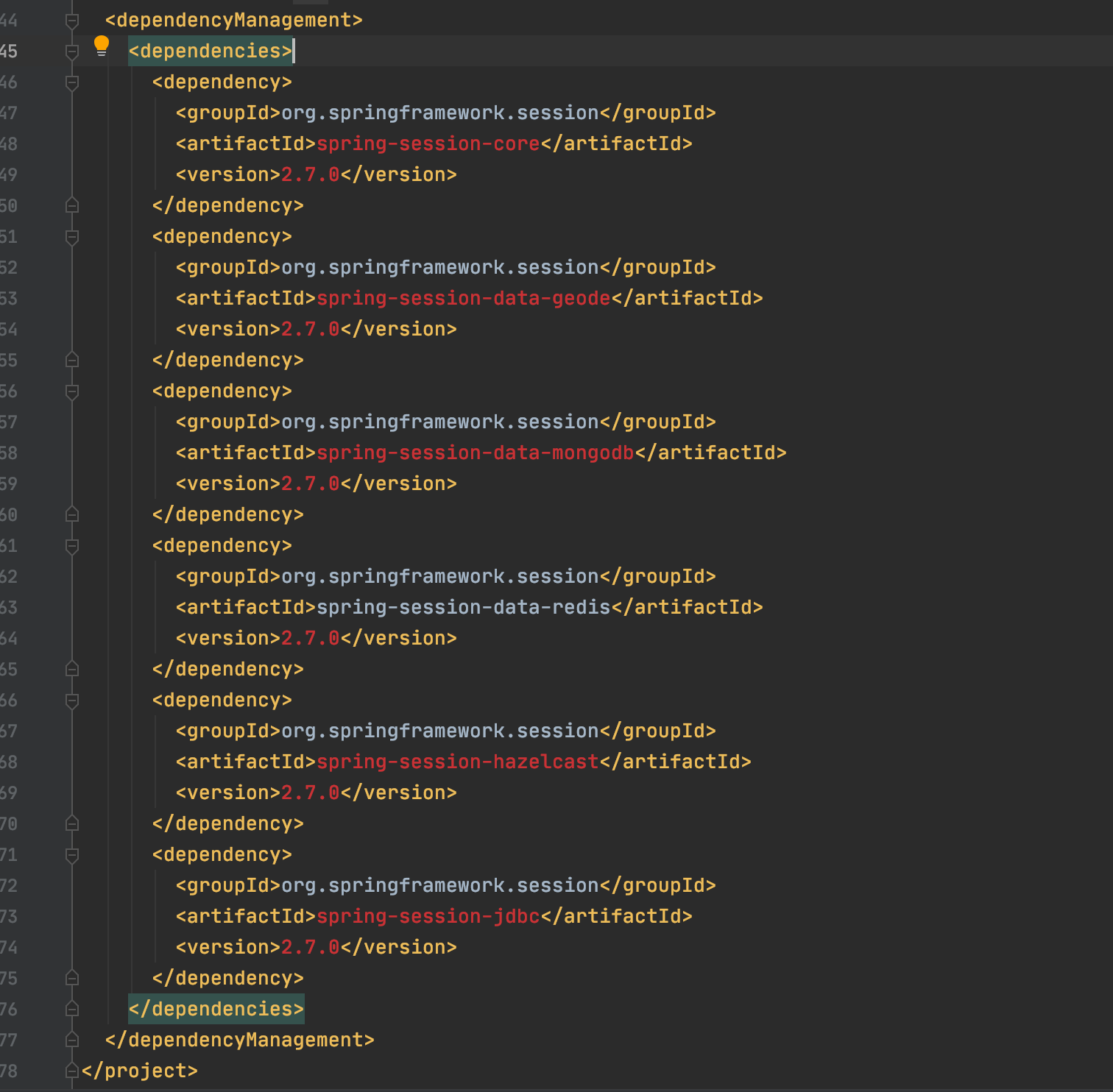
聊聊Maven的依赖传递、依赖管理、依赖作用域

1. 依赖传递 在Maven中&#xff0c;依赖是会传递的&#xff0c;假如在业务项目中引入了spring-boot-starter-web依赖&#xff1a; <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId>…...

编程日记 2023/10/15 9:42:11

centos6/7 SOCKS5 堆溢出漏洞修复（RPM方式）curl 8.4 CVE-2023-38545 CVE-2023-38546

引用 https://darkdark.top/update-curl.html centos6 rpm 升级包下载&#xff1a;https://download.csdn.net/download/sinat_24092079/88425840 yum update libcurl-8.4.0-1.el6.1.x86_64.rpm curl-8.4.0-1.el6.1.x86_64.rpmcentos7 rpm 升级包下载&#xff1a;https://down…...

编程日记 2023/10/15 9:41:07

C#，数值计算——数据建模Proposal的计算方法与源程序

1 文本格式 using System; namespace Legalsoft.Truffer { public class Proposal { public Normaldev gau { get; set; } null; private double logstep { get; set; } public Proposal(int ranseed, double lstep) { this.gau…...

编程日记 2023/10/15 9:40:05

如何使用命令生成动态链接库.dll文件（保姆级教学）

如何使用命令生成动态链接库.dll文件 /*** file 如何使用命令生成动态链接库.dll文件* author jUicE_g2R(qq:3406291309)* * brief 教学演示* tool visual studio2022&#xff08;2019也适用&#xff09;* * copyright 2023.10* COPYR…...

编程日记 2023/10/15 9:39:04

Qt之模块介绍

Qt提供了很多功能模块&#xff0c;我们需要知道的是这些模块有些加入了标准库&#xff0c;有一些并没有加入到标准库。至于为什么没有加入到标准库通过chatgpt得到的答案如下&#xff1a; Qt 是一个强大的跨平台 C 框架&#xff0c;它包括了很多核心模块和功能&#xff0c;以支…...

编程日记 2023/10/15 9:38:03

Socks5代理和代理IP

在数字时代&#xff0c;网络工程师必须不断掌握新技术&#xff0c;以解决跨界电商、爬虫数据采集、出海业务扩展、网络安全保护以及游戏性能优化等各种技术挑战。本文将深入探讨Socks5代理和代理IP技术&#xff0c;它们在各个领域中的应用&#xff0c;如何为网络工程师提供了强…...

编程日记 2023/10/15 9:37:01

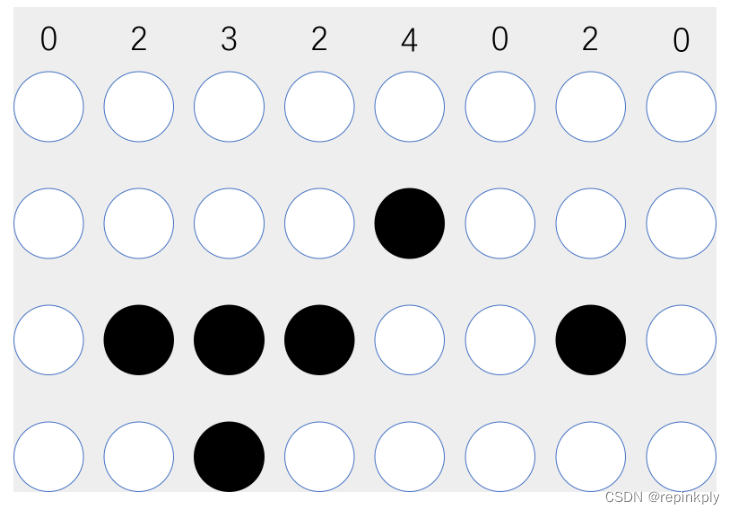
计算机指令、机器码

目录 背景 在软硬件接口中&#xff0c;CPU 帮我们做了什么事&#xff1f; 从编译到汇编&#xff0c;代码怎么变成机器码&#xff1f; 解析指令和机器码 总结延伸 背景 上大学的时候&#xff0c;我们系里教 C 语言程序设计的老师说&#xff0c;他们当年学写程序的时候&…...

编程日记 2023/10/15 9:36:00

MyLife - Docker安装Consul

Docker安装Consul 个人觉得像consul之类的基础设施在线上环境直接物理机安装使用可能会好些。但是在开发测试环境用docker容器还是比较方便的。这里学习下docker安装consul使用。 1. Consul 镜像库地址 Consul 镜像库地址&#xff1a;https://hub.docker.com/r/hashicorp/consu…...

编程日记 2023/10/15 9:34:59

Leetcode刷题笔记--Hot61-70

1--课程表&#xff08;207&#xff09; 主要思路&#xff1a; 用 in 记录每一门课程剩余的先修课程个数&#xff0c;当剩余先修课程个数为0时&#xff0c;将该课程加入到队列q中。 每修队列q中的课程&#xff0c;以该课程作为先修课程的所有课程&#xff0c;其剩余先修课程个数…...

编程日记 2023/10/15 9:33:57

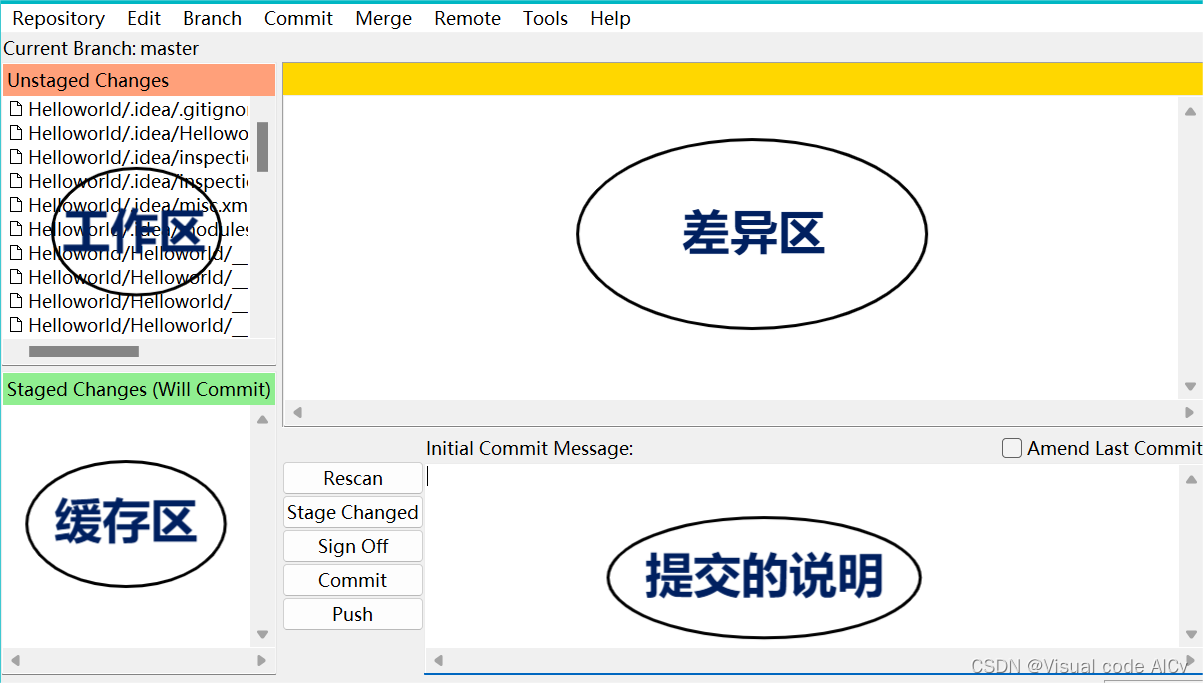
python特别篇—github基本操作手册

一、开始使用 1.1 “Hello world” 1.1.1 github介绍 GitHub是一个基于Git版本控制系统的代码托管平台。它提供了一个在线的代码仓库&#xff0c;使开发者可以将自己的代码存储在云端&#xff0c;并与其他开发者进行协作。GitHub不仅仅是一个代码托管平台&#xff0c;还提供了…...

编程日记 2023/10/15 9:32:56

tiktok直播websocket序列化与反序列化

系列文章目录 websocket训练地址：https://www.qiulianmao.com，正在搭建中 基础-websocket逆向基础-http拦截基础-websocket拦截基础-base64编码与解码基础-protobuf序列化与反序列化视频号直播弹幕采集tiktok protobuf序列化与反序列化实战一：Http轮询更新中tikto...

编程日记 2023/10/15 9:30:55

K8S认证|CKS题库+答案| 11. AppArmor

目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作&#xff1a; 1&#xff09;、切换集群 2&#xff09;、切换节点 3&#xff09;、切换到 apparmor 的目录 4&#xff09;、执行 apparmor 策略模块 5&#xff09;、修改 pod 文件 6&#xff09;、…...

编程新知 2025/7/2 19:20:58

Cesium1.95中高性能加载1500个点

一、基本方式&#xff1a; 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

编程新知 2025/6/17 7:02:51

FastAPI 教程：从入门到实践

FastAPI 是一个现代、快速&#xff08;高性能&#xff09;的 Web 框架&#xff0c;用于构建 API&#xff0c;支持 Python 3.6。它基于标准 Python 类型提示&#xff0c;易于学习且功能强大。以下是一个完整的 FastAPI 入门教程&#xff0c;涵盖从环境搭建到创建并运行一个简单的…...

编程新知 2025/6/25 16:32:53

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2025/7/3 13:21:09

全面解析各类VPN技术：GRE、IPsec、L2TP、SSL与MPLS VPN对比

目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec&#xff1f; IPsec VPN 5.1 IPsec传输模式&#xff08;Transport Mode&#xff09; 5.2 IPsec隧道模式&#xff08;Tunne…...

编程新知 2025/6/17 4:01:05

如何理解 IP 数据报中的 TTL？

目录 前言理解 前言 面试灵魂一问&#xff1a;说说对 IP 数据报中 TTL 的理解&#xff1f;我们都知道&#xff0c;IP 数据报由首部和数据两部分组成&#xff0c;首部又分为两部分&#xff1a;固定部分和可变部分&#xff0c;共占 20 字节&#xff0c;而即将讨论的 TTL 就位于首…...

编程新知 2025/6/26 9:15:41

如何在网页里填写 PDF 表格？

有时候&#xff0c;你可能希望用户能在你的网站上填写 PDF 表单。然而&#xff0c;这件事并不简单&#xff0c;因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件&#xff0c;但原生并不支持编辑或填写它们。更糟的是&#xff0c;如果你想收集表单数据&#xff…...

编程新知 2025/7/3 1:16:15

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/6/24 5:38:28

初探Service服务发现机制

1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能&#xff1a;服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源&#xf…...

编程新知 2025/6/26 4:10:00

Kafka入门-生产者

生产者 生产者发送流程&#xff1a; 延迟时间为0ms时&#xff0c;也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于&#xff1a;异步发送不需要等待结果&#xff0c;同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

编程新知 2025/7/1 15:01:34