蓝桥杯 枚举算法 (c++)

枚举就是根据提出的问题,——列出该问题的所有可能的解,并在逐一列出的过程中,检验每个可能解是否是问题的真正解,
如果是就采纳这个解,如果不是就继续判断下一个。
枚举法一般比较直观,容易理解,但由于要检查所有的可能解,因此运行效率较低。
能够用枚举法解决的题目往往是最简单的一类题目。这种题具有以下特点:
·解枚举范围是有穷的。
·检验条件是确定的。
先来看一个简单的问题。
某君说:“我的年龄是个两位数,我比儿子大27岁,如果把我的年龄的两位数字交换位置,刚好就是我儿子的年龄”
请你计算:某君的年龄一共有多少种可能情况?
我们来分析一下这道题。题里给出某君的年龄是两位数,那么年龄的取值范围是[10,99]内的整数。
检验条件也是确定的,只要把枚举的年龄的个位与十位交换,如果发现比原数字刚好小27,那么它就是真正的解。
以上的解决思路就是枚举法的一个例子。
#include<iostream>
using namespace std;
int main(){int total=0;//记录可能解的个数 for(int i=10;i<=99;i++){//枚举年龄范围 if(i=(i%10)*10+i/10+27){total++;}}cout<<total<<endl;return 0;
}
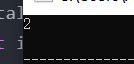
在判断条件中,我们通过对10取模的方式来获取一个数的个位数。用除10的方法来获取一个数的十位数。(在程序中整型数字与整型数字相除表示整除,所以除10会让数字的个位数字被舍去,其余的十进制每一位向右移动一位。)
这道题是第七届蓝桥杯C/C++语言A组的题目。
前面的课程里,我们已经学习了如何输出1到100
范围内的所有质数。接下来,我们要实现输出n到m之间所有质数的程序。n,m保证为正整数。
首先,我们肯定需要定义并读入两个整数n,m,把
int n;
修改为:
int n,n;
cin>>n>>m;
并将外层循环结构改为
for(int j=n;j<=m;j++){}
#include<iostream>
using namespace std;
int main(){int n,m;cin>>n>>m;for(int j=n;j<=m;j++){if(j==1){continue;}bool is_prime=true;for(int i=2;i<j;i++){if(j%i==0){is_prime=false;break;}}if(is_prime){cout<<j<<endl;}}return 0;
}
观察数字:12321,123321都有一个共同的特征,就是无论从左到右读还是从右向左读,都是相同的。这样的数字叫做回文数字。
现在要从5位或6位的十进制数字中找出各个数位之和等于n的回文数字。
输入格式
输入一个整数n(10≤n≤100)。
输出格式
输出所有各个数位之和等于n的5位和6位整数,每个数字占一行,
数字按从小到大的顺序排列。如果没有满足条件的数字,则输出-1.
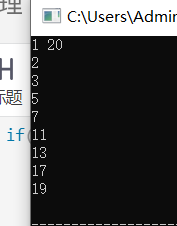
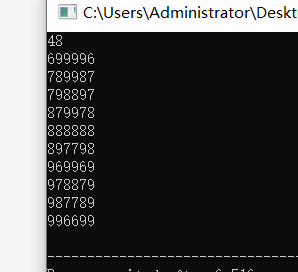
样例输入
48
样例输出
699996
789987
798897
879978
888888
897798
969969
978879
987789
996699
#include<iostream>
using namespace std;
int n;
int digit[6];
bool judge(int x){int m=0,sum=0;while(x){digit[m++]=x%10;sum+=x%10;x/=10;}if(sum!=n){return false;}for(int i=0;i<m/2;i++){if(digit[i]!=digit[m-1-i]){return false;}}return true;}int main(){bool f = false;cin>>n;for(int i=10000;i<1000000;i++){if(judge(i)){cout<<i<<endl;f=true;}}if(!f){cout<<-1<<endl;}return 0;}
如果一个4位数,它的每个位上的数字的4次幕之和等于它本身,那么我们就称这个数字为一个四叶玫瑰数。现在,我们要求出n以内所有的四叶玫瑰数。
首先,我们读入了一个整数n,由于四叶玫瑰数一定是个四位数,那我们首先将其它位数的数字排除,请在return 0;之前写:
if(n<1000||n>9999){cout<<"error!";
}else{}
接下来,我们要依次枚举从1000开始到n之间的数字,哪些符合四叶玫瑰数的要求,并将它输出。在这里,我们将判断四叶玫瑰数的代码封装成一个自己定义的函数rose,我们先在else分支中写:
for(int i=1000;i<=n;i++){if(rose(i)){cout<<i<<endl;}
}
输入一个四位数n,看看1000到n之间有没有四
叶玫瑰数吧。
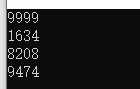
·事实上,一共有三个四叶玫瑰数,他们分别是
1634,8208,9474
#include<iostream>
#include<cmath>
using namespace std;
bool rose(int i){int a=i/1000,b=i/100%10,c=i/10%10,d=i%10;int ans=a*a*a*a+b*b*b*b+c*c*c*c+d*d*d*d;if(ans==i){return true;}else{return false;}
}
int main(){int n;cin>>n;if(n<1000||n>9999){cout<<"error!";}else{for(int i=1000;i<=n;i++){if(rose(i)){cout<<i<<endl;}}}
}
某君从某年开始每年都举办一次生日party,并且每次都要吹熄与年龄相同根数的蜡烛。现在算起来,他一共吹熄了236根蜡烛。那么,他从几岁开始过生日party的。从常识来讲一个人的年龄不可能超过200岁。
因此,我们需要枚举这个人的开始过生日的年龄,
从0到200,请在return 0:之前写:
for(int i=1;i<=200;i++){}
接下来,我们需要依次枚举他从某岁到某岁之间会吹多少蜡烛。如果这个数目超过236,我们就不关心了;同时,我们并不知道这中间过了多少岁,所以无法确定循环次数,因此这里使用while循环更合适,请在for循环中写:
int can=0,j=i;
while(can<236&&j<=200){can+=j;j++;
}
其中,变量can用于记录蜡烛数目,j是一个累加变量。
跳出while循环后,如果蜡烛的数目恰好等于236
,说明枚举条件成立,变量的值就是他开始过
生日时的年龄。
请接着写:
if(can==236){cout<<i<<endl;
}
其中,变量can用于记录蜡烛数目,j是一个累加变量。
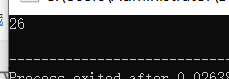
运行一下,看看结果是不是26。
想一想,如果我们还想知道他今年多少岁,应该怎
么做呢?
#include<iostream>
using namespace std;
int main(){for(int i=1;i<=200;i++){int can=0,j=i;while(can<236&&j<=200){can+=j;j++;}if(can==236){cout<<i<<endl;}}return 0;
}
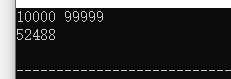
有些人很迷信数字,比如认为带4的数不吉利。某抽奖活动的奖券号码是5位数(10000-99999),要求其中不要出现带“4”的
号码,主办方想让你计算一下,如果发行号码n到m之间的奖券,在任何两张奖券都不重复的情况下,可以发行多少张?
输入格式
输入为一行,为两个空格隔开的整数n,m,
10000 <=n <=m <=99999.
输出格式
输出为一个整数,为可发出奖券的数目。
样例输入
10000 99999
样例输出
52488
#include<iostream>
using namespace std;
bool judge(int x){while(x){if(x%10==5){return true;}x/=10;}return false;
}
int main(){int n,m,cnt=0;cin>>n>>m;for(int i=n;i<=m;i++){if(!judge(i)){cnt++;}}cout<<cnt<<endl;return 0;
}
相关文章:

蓝桥杯 枚举算法 (c++)
枚举就是根据提出的问题,——列出该问题的所有可能的解,并在逐一列出的过程中,检验每个可能解是否是问题的真正解, 如果是就采纳这个解,如果不是就继续判断下一个。 枚举法一般比较直观,容易理解࿰…...
Wordpress自定义小工具logo调用设置(可视化)
在主题开发中,需要调用网站的logo,最简单的办法就是用wp自带的函数,那就是the_custom_logo(),使用它还可以通过后台-自定义-logo,边修改边预览,还是很香的。 自定义徽标支持应首先使用add_theme_support()添…...
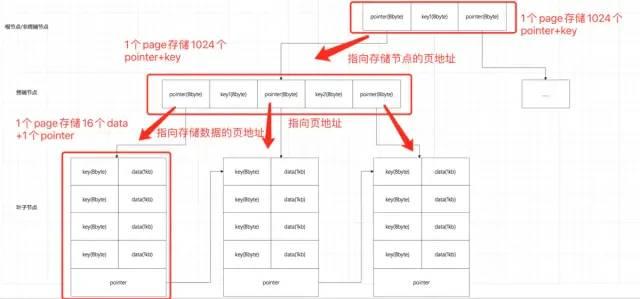
面试常考数据结构:红黑树、B树、B+树各自适用的场景
1. 磁盘基础知识 分页: 现代操作系统都使用虚拟内存来印射到物理内存,内存大小有限且价格昂贵,所以数据的持久化是在磁盘上。虚拟内存、物理内存、磁盘都使用页作为内存读取的最小单位。一般一页为4KB(8个扇区,每个扇…...
Paddle GPU版本需要安装CUDA、CUDNN
完整的教程 深度学习环境配置:linuxwindows系统下的显卡驱动、Anaconda、Pytorch&Paddle、cuda&cudnn的安装与说明 - 知乎这篇文档的内容是尽量将深度学习环境配置(使用GPU)所需要的内容做一些说明,由于笔者只在windows和linux下操作过…...

MYSQL length函数
mysql length函数计算结果的单位是啥,和varchar字段类型的单位是相同的吗? 做了一下实验,结果如下: 1.mysql length 函数计算的是有多少个字符,比如字段值是 permission 则length函数计算结果为10。 2.如果字段类型是…...

uniapp 在android手机上运行tab栏页面跳转问题
【问题描述】: 使用uniapp写的项目,在tab页面,无论使用哪种方式的跳转,只要是在url后面拼接参数,在打包成apk文件后,在手机上面安装使用,都是获取不到susIndex参数的,而在浏览器上面…...

css3 hover效果
CSS3中的:hover伪类用于创建鼠标悬停时的样式效果。当用户将鼠标悬停在页面元素上时,你可以为这些元素定义不同的样式规则,以实现交互效果 /* 一般样式规则 */ element {/* 正常状态下的样式 */ }/* 悬停样式规则 */ element:hover {/* 鼠标悬停时的样式…...
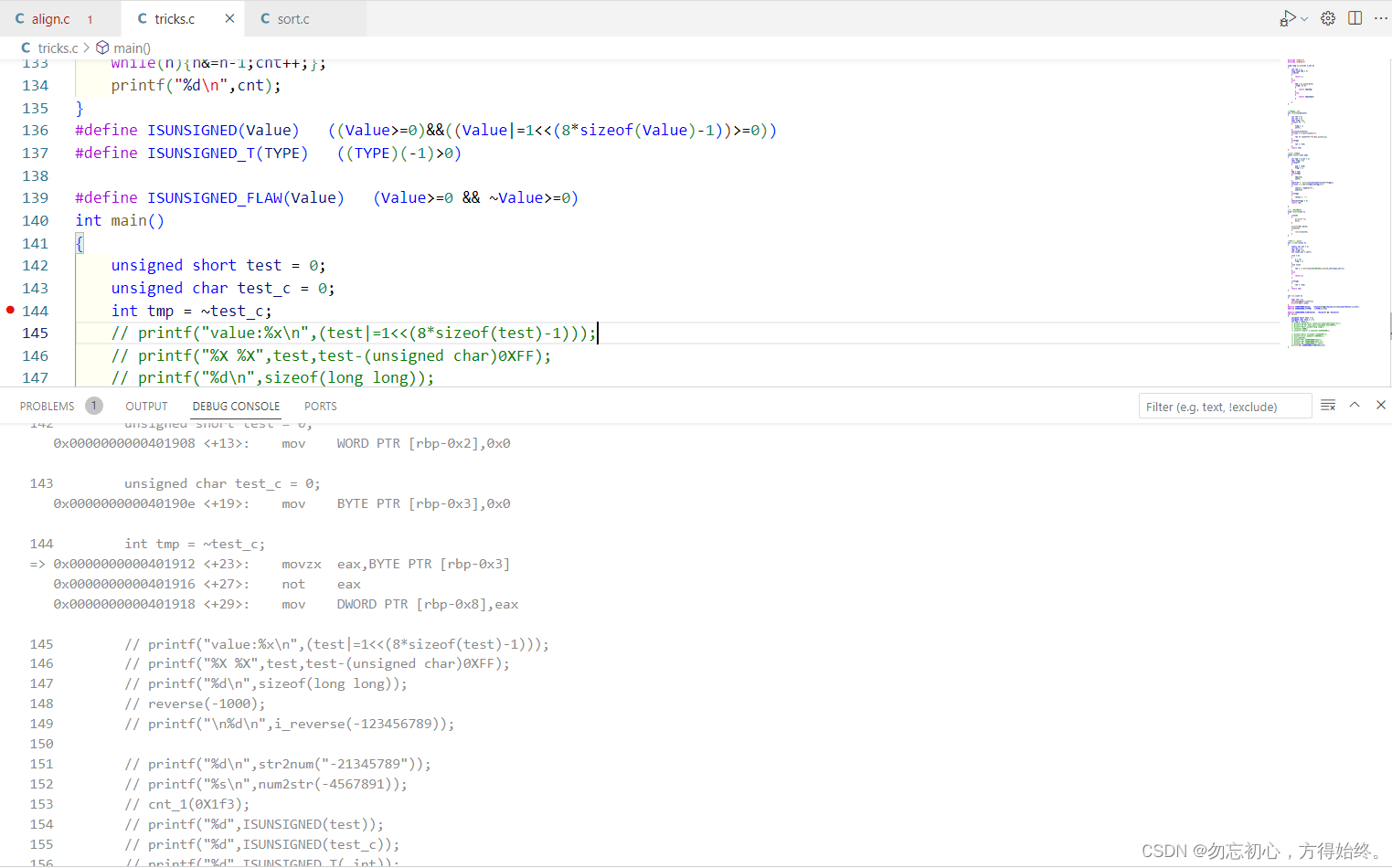
C语言char与short取反以及符号判断问题
这个问题主要是在从对一个变量进行符号判断引出,有一种判断方法是#define ISUNSIGNED(Value) (Value >0 && ~Value >0) 主要是通过将符号位取反然后将变量与0进行比较。传入int与unsigned int结果正确,但是当传入unsigned char 与unsign…...

Gpt-4多模态功能强势上线,景联文科技多模态数据采集标注服务等您来体验!
就在上个月,OpenAI 宣布对ChatGPT 进行重大更新,该模型不仅能够通过文字输入进行识别和分析,还能够通过语音、图像甚至视频等多种模态的输入来获取、识别、分析和输出信息。这一重要技术突破,将促进多模态自然语言处理的发展&…...

【idea】 java: 找不到符号
idea 启动时提示 java: 找不到符号 java: 找不到符号 符号: 方法 getCompanyDisputeCount() 位置: 类型为com.yang.entity.AreaAnalyse的变量 areaAnalyse 在setting ——> Compiler ——>Shared build process VM options: 添加: -Djps.track.ap.dep…...

Flink测试利器之DataGen初探 | 京东云技术团队
什么是 Flinksql Flink SQL 是基于 Apache Calcite 的 SQL 解析器和优化器构建的,支持ANSI SQL 标准,允许使用标准的 SQL 语句来处理流式和批处理数据。通过 Flink SQL,可以以声明式的方式描述数据处理逻辑,而无需编写显式的代码…...
)
linux更换常用软件的默认缓存路径(.conda, .huggingface等)
在使用linux的过程中,我们往往会使用软件安装很多packages,其中的大多数软件(例如conda)会把当前安装的packages缓存起来,以加速之后的相同package的安装。 而很多软件的默认缓存路径是user自己的home路径。下面罗列几…...
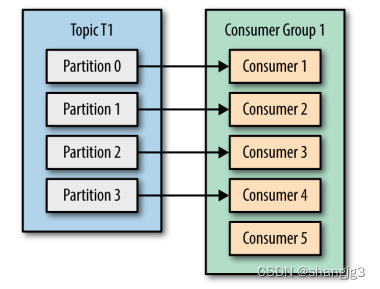
Kafka消费者使用案例
本文代码链接:https://download.csdn.net/download/shangjg03/88422633 1.消费者和消费者群组 在 Kafka 中,消费者通常是消费者群组的一部分,多个消费者群组共同读取同一个主题时,彼此之间互不影响。Kafka 之所以要引入消费者群组…...
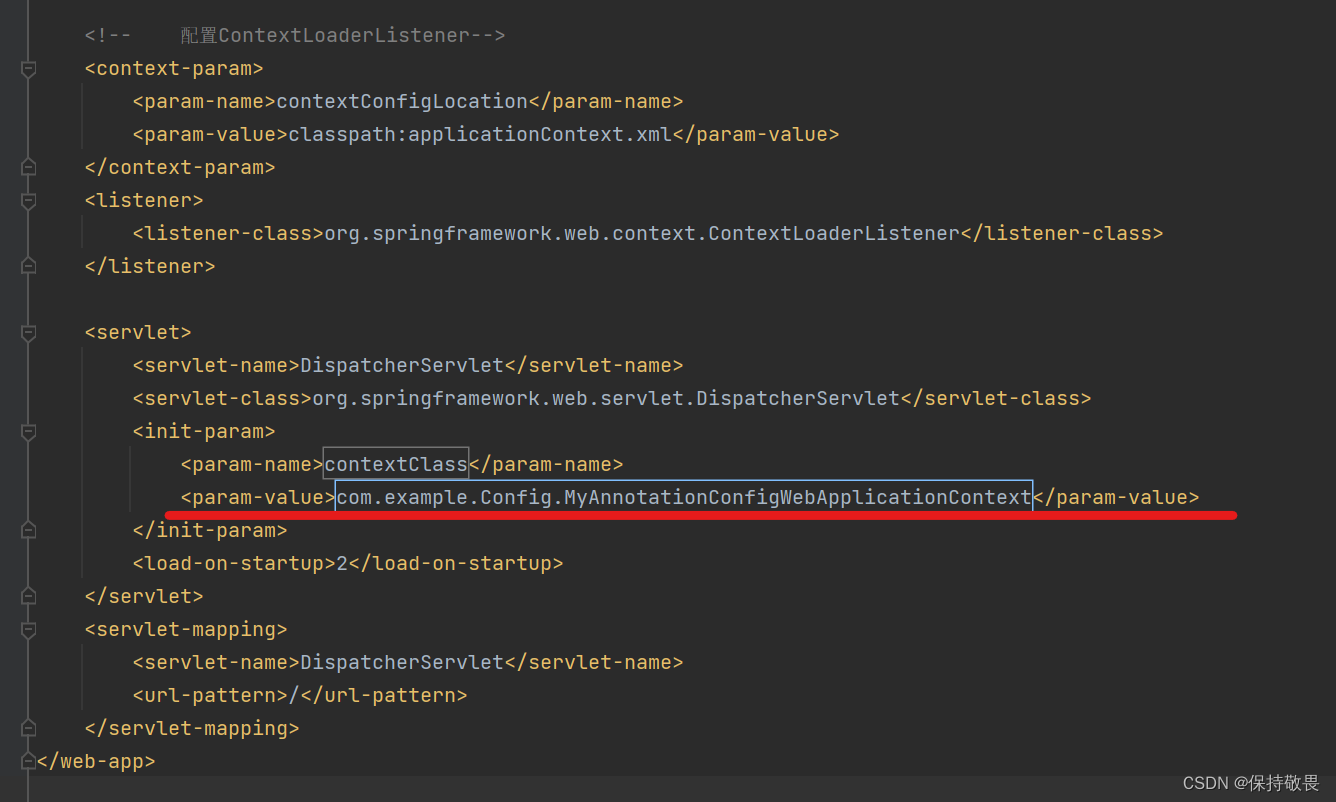
SpringMVC全注解开发
在学习过程中,框架给我们最大的作用,就是想让开发人员尽可能地只将精力放在具体业务功能的实现之上,而对于各种映射关系的配置,统统由框架来进行完成,由此,注解就很好的将映射功能进行实现,并且…...

解决 android Cannot access ‘<init>‘: it is private in
最近要在2个非直接依赖module使用单例,有一种注入依赖的方式可以,但是报了如下错误: Cannot access <init>: it is private in 经过查阅资料,原来是依赖的单例类的构造函数不能使用private,这里做个记录&#…...
不容易解的题10.15
395.至少有K个重复字符的最长字串 395. 至少有 K 个重复字符的最长子串 - 力扣(LeetCode)https://leetcode.cn/problems/longest-substring-with-at-least-k-repeating-characters/description/?envTypelist&envIdZCa7r67M自认为是不好做的题。尤其…...
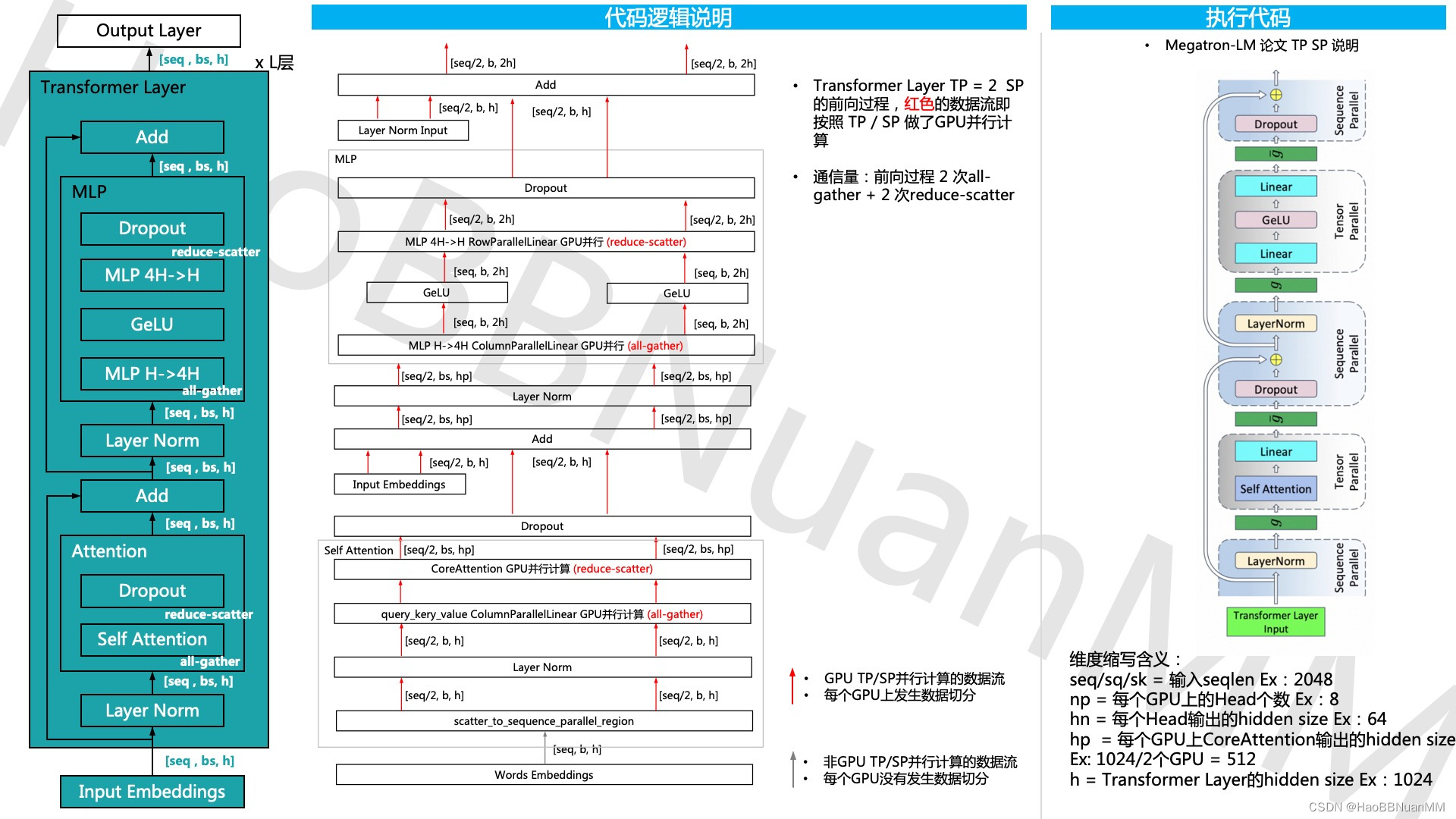
Megatron-LM GPT 源码分析(二) Sequence Parallel分析
引用 本文基于开源代码 https://github.com/NVIDIA/Megatron-LM ,延续上一篇Megatron-LM GPT 源码分析(一) Tensor Parallel分析 通过对GPT的模型运行示例,从三个维度 - 模型结构、代码运行、代码逻辑说明 对其源码做深入的分析。…...
 rust解法)
DNA序列(DNA Consensus String, ACM/ICPC Seoul 2006, UVa1368) rust解法
输入m个长度均为n的DNA序列,求一个DNA序列,到所有序列的总Hamming距离尽量小。两个等长字符串的Hamming距离等于字符不同的位置个数,例如,ACGT和GCGA的Hamming距离为2(左数第1, 4个字符不同)。 输入整数m和…...

如何使用Jmeter进行http接口测试?
前言: 本文主要针对http接口进行测试,使用Jmeter工具实现。 Jmter工具设计之初是用于做性能测试的,它在实现对各种接口的调用方面已经做的比较成熟,因此,本次直接使用Jmeter工具来完成对Http接口的测试。 一、开发接…...
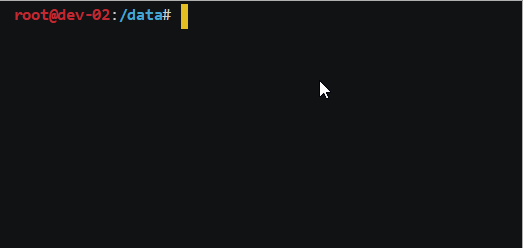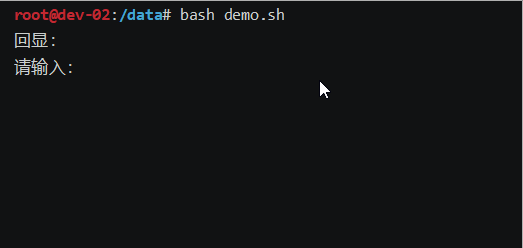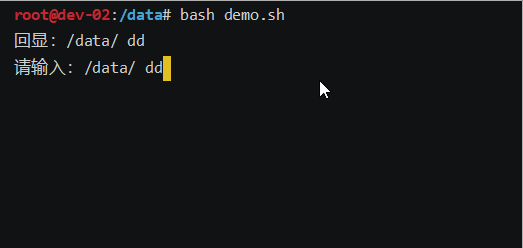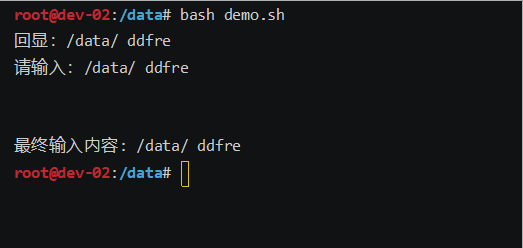
bash一行输入,多行回显demo脚本
效果图: 脚本: #!/bin/bash # 定义一个变量,用来存储输入的内容 input"" # 定义一个变量,用来存储输入的字符 char""# 为了让read能读到空格键 IFS_store$IFS IFS# 提示内容,在while循环中也有&a…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
