Java实现B树
1.介绍
B树是一种自平衡的搜索树数据结构,常用于数据库和文件系统中的索引结构。它具有以下好处和功能:
-
高效的查找操作:B树的特点是每个节点可以存储多个关键字,并且保持有序。通过在节点上进行二分查找,可以快速定位目标关键字的位置,从而实现高效的查找操作。
-
平衡性:B树通过自平衡的方式维护树的平衡性,即保证树的每个叶子节点到根节点的路径长度相等。这种平衡性能够确保各种操作的时间复杂度保持在较低水平,例如插入、删除和查找等操作都可以在对数时间内完成。
-
适应大型数据集:B树适用于存储大型数据集,并且可以处理非常大的索引。其节点可以存储多个关键字,因此在相同层数的情况下,B树可以存储更多的数据。
-
支持范围查询:由于B树的节点有序,因此可以很方便地进行范围查询。通过定位范围的起始和结束关键字所在的节点,可以快速地获取指定范围内的数据。
-
高效的插入和删除操作:B树通过平衡性的维护,使得插入和删除操作具有较低的时间复杂度。它可以通过调整节点的结构,避免过深或过浅的树结构,从而保持树的平衡。
总的来说,B树是一种高效的数据结构,能够应对大规模数据集的索引需求,并提供快速的查找、插入和删除操作。它在数据库和文件系统中广泛应用,为数据的组织和访问提供了便利。
2.代码分析
1.分裂
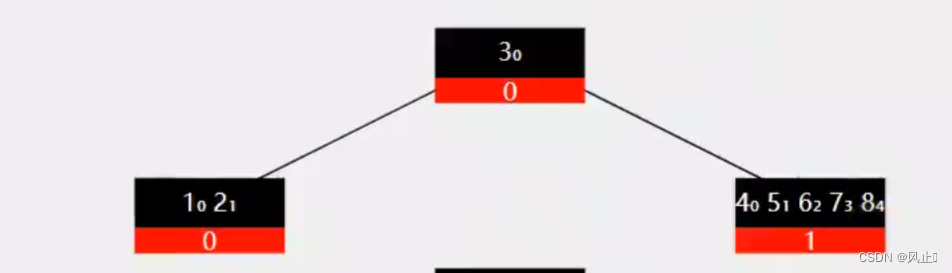
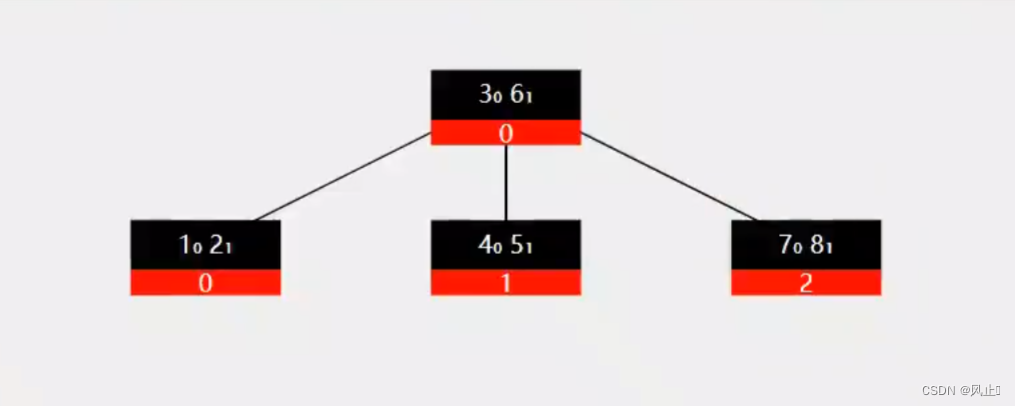
当键的数量超过 2t - 1的时候就会进行分裂操作,规则就是中间的向上分裂,大的交给一个新的节点,小的交给自己
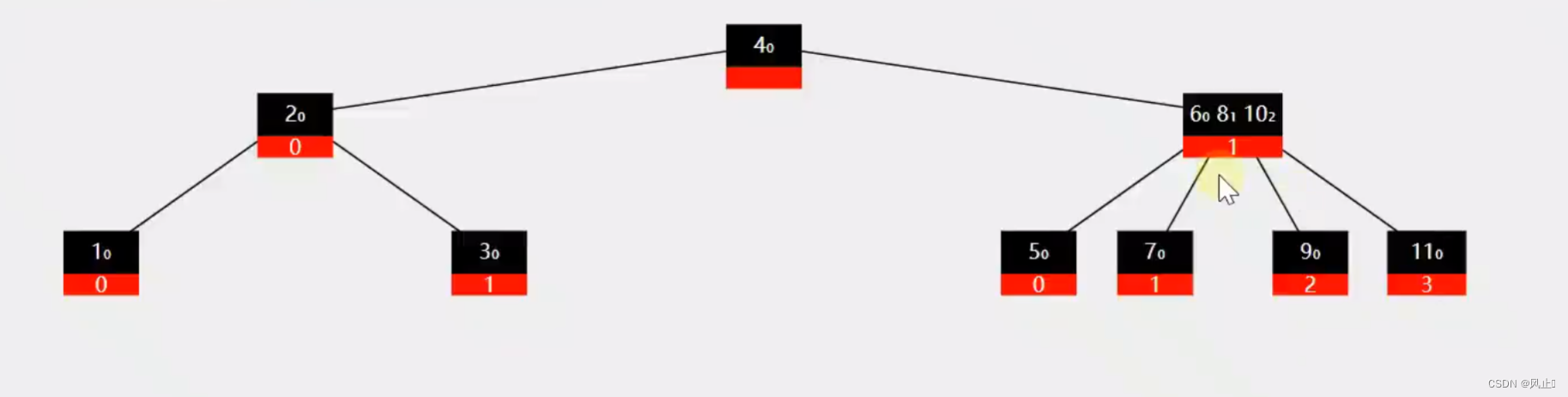
如果不是叶子节点就需要把后半部分子节点给新的节点,
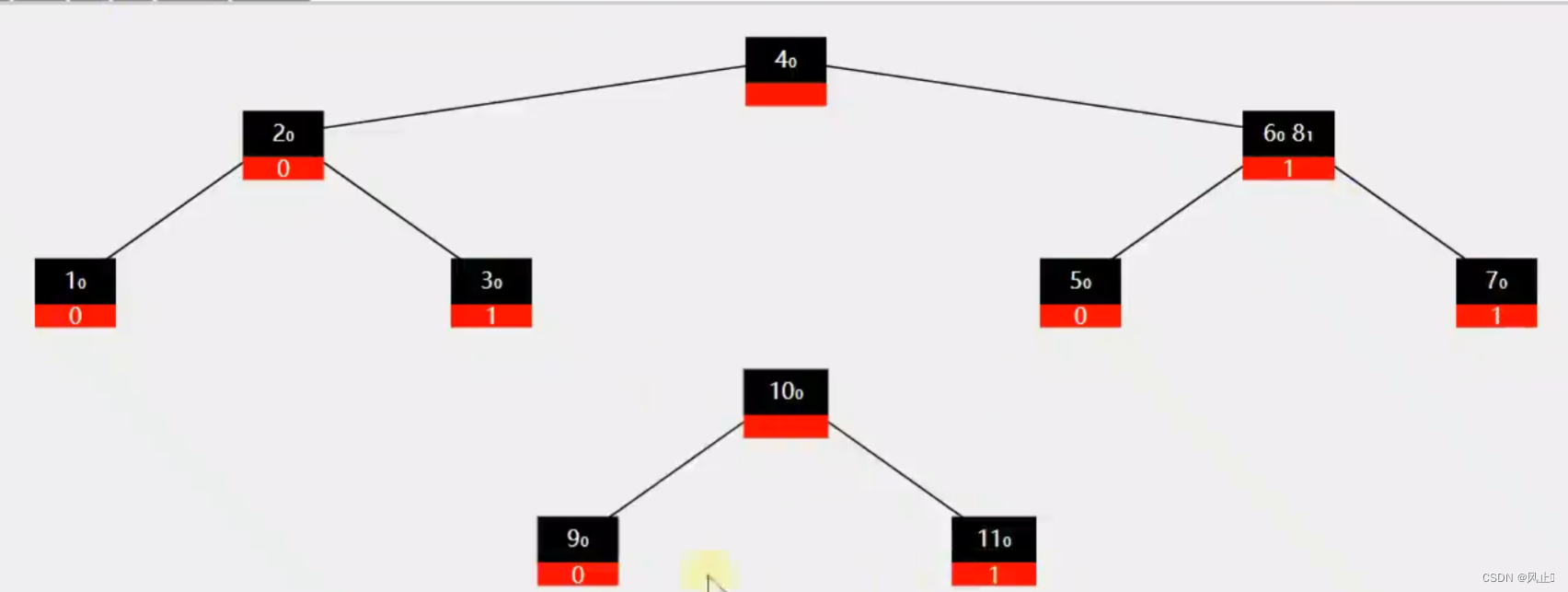
2.添加
-
首先,根据给定的关键字,从根节点开始向下搜索,找到合适的叶子节点。
-
在叶子节点中插入新的关键字。如果叶子节点未满,直接插入;否则,执行步骤3。
-
当叶子节点已满时,需要进行分裂操作。将当前节点一分为二,得到两个新的叶子节点,并选择一个关键字提升到父节点中。
-
如果父节点也已满,则重复步骤3,层层递归地向上分裂,直到找到一个非满节点或达到树的顶部。
-
完成插入操作后,需要更新祖先节点的关键字信息。如果某个节点发生了分裂,它提升的关键字需要插入到其父节点中,并根据大小顺序进行调整。
通过以上步骤,B树的插入操作可以保持树的平衡性。在插入过程中,B树会根据节点的容量进行自动调整,使得树的高度保持相对较低,从而确保各种操作的效率。
需要注意的是,在插入操作中可能会出现关键字重复的情况。对于B树来说,可以允许存在相同的关键字,而在查找操作时,会按照节点中关键字的大小顺序进行搜索。因此,在插入过程中需要根据具体需求来处理关键字重复的情况。
3.查找
-
从根节点开始,比较要查找的关键字与当前节点中的关键字。
-
如果找到了匹配的关键字,则表示查找成功,结束操作。
-
如果要查找的关键字小于当前节点的最小关键字,则进入当前节点的左子树进行继续查找。
-
如果要查找的关键字大于当前节点的最大关键字,则进入当前节点的右子树进行继续查找。
-
重复步骤 3 和 4,直到找到匹配的关键字或者到达叶子节点。
-
如果到达叶子节点仍然没有找到匹配的关键字,则表示查找失败,结束操作。
在B树的查找过程中,关键字的比较会指导搜索方向,通过不断地按照关键字的大小顺序向下搜索,可以快速地找到目标关键字或者判断其不存在。
需要注意的是,B树中允许存在相同的关键字,因此在查找操作中,如果存在多个相同的关键字,可以根据具体需求选择返回其中一个或全部。此外,B树的查找操作具有较好的平均时间复杂度,可以在较短的时间内完成查询。
3.代码实现
1.准备工作
//节点类
class BTreeNode {// B树的阶数int t;List<Integer> keys;//关键字List<BTreeNode> childNodes;//孩子boolean leaf;//判断节点是否是叶子结点public BTreeNode(int t, boolean leaf) {this.t = t;this.leaf = leaf;this.keys = new ArrayList<>();this.childNodes = new ArrayList<>();}
}2.升序遍历树
public void traverse() {int i;for (i = 0; i < keys.size(); i++) {if (!leaf) {//去索引为i的孩子里面继续找childNodes.get(i).traverse();}System.out.print(keys.get(i) + " ");}//最后还剩一个关键字的孩子节点if (!leaf) {childNodes.get(i).traverse();}}3.查找值所在的位置
public int search(int key) {int i = 0;//先找到比值小和等的节点 然后小的递归找孩子while (i < keys.size() && key > keys.get(i)) {i++;}//等的if (i < keys.size() && key == keys.get(i)) {return i;} else if (leaf) {//都到叶子了还没找到就无了return -1;} else {//递归继续去他的子节点找 小的return childNodes.get(i).search(key);}}4.添加
public void insertNonFull(int key) {//处理节点未满的情况int i = keys.size() - 1;if (leaf) {//叶节点while (i >= 0 && key < keys.get(i)) {//从后往前 找出比你小的那个ii--;}keys.add(i + 1, key);//因为第i个位置是比你小的,所以你要插入后面一个} else {//非叶节点while (i >= 0 && key < keys.get(i)) {//找到要插入子节点的位置i--;}//判断子节点是否需要分裂操作if (childNodes.get(i + 1).keys.size() == (2 * t) - 1) {splitChild(i + 1, childNodes.get(i + 1));if (key > keys.get(i + 1)) {i++;}}//分裂完毕 或者 不需要分裂 递归插入childNodes.get(i + 1).insertNonFull(key);}}5.分裂
public void splitChild(int i, BTreeNode y) {//处理节点满的情况进行分裂操作BTreeNode z = new BTreeNode(y.t, y.leaf);keys.add(i, y.keys.get(t - 1));//中间的上移childNodes.add(i + 1, z);//创建新的孩子for (int j = 0; j < t - 1; j++) {//后面的移动到新的里面z.keys.add(j, y.keys.get(j + t));}if (!y.leaf) {//后半部分子节点移动到新的节点for (int j = 0; j < t; j++) {z.childNodes.add(j, y.childNodes.get(j + t));}}//主要总用时为了情况没有用的部分//获取被拆分节点后半部分的关键字和子节点部分。y.keys.subList(t - 1, y.keys.size()).clear();//方法用于删除列表中的元素(获取完删除)y.childNodes.subList(t, y.childNodes.size()).clear();}
}6.遍历查询
class BTree {BTreeNode root;//根节点int t;//树中的最小度数//指定默认树的度数是2public BTree() {this(2);}public BTree(int t) {this.root = null;this.t = t;}//遍历树public void traverse() {//树不为空就可以遍历if (root != null) {root.traverse();}}//查找节点的位置public int search(int key) {if (root != null) {return root.search(key);}return -1;}//插入节点public void insert(int key) {if (root == null) {root = new BTreeNode(t, true);root.keys.add(0, key);} else {if (root.keys.size() == (2 * t) - 1) {BTreeNode s = new BTreeNode(t, false);s.childNodes.add(0, root);s.splitChild(0, root);int i = 0;if (s.keys.get(0) < key) {i++;}s.childNodes.get(i).insertNonFull(key);root = s;} else {root.insertNonFull(key);}}}
}相关文章:

Java实现B树
1.介绍 B树是一种自平衡的搜索树数据结构,常用于数据库和文件系统中的索引结构。它具有以下好处和功能: 高效的查找操作:B树的特点是每个节点可以存储多个关键字,并且保持有序。通过在节点上进行二分查找,可以快速定位…...
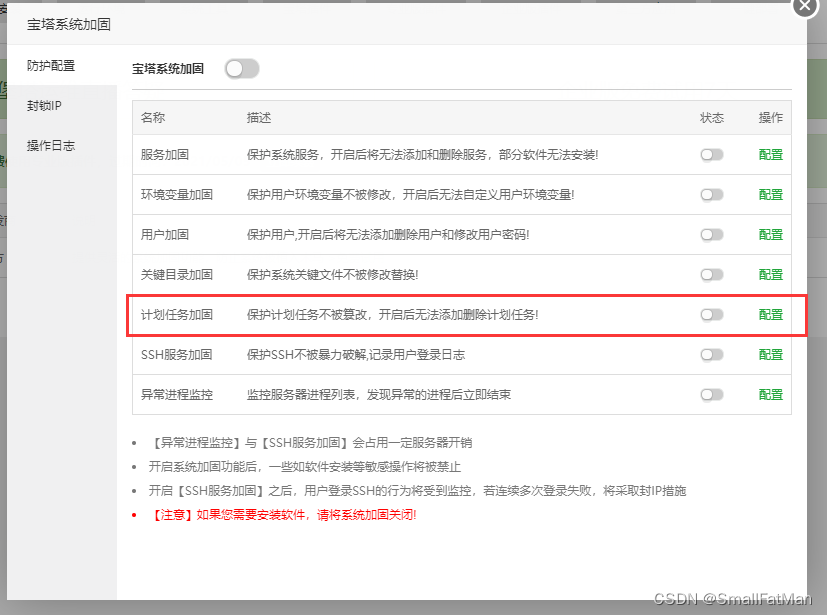
crontab报错/var/spool/cron : Permission denied和 -bash: chattr: command not found
crontab报错/var/spool/cron : Permission denied和 -bash: chattr: command not found 1、第一种情况2、第二种情况3、第三种情况 1、第一种情况 centos7下修改定时任务crontab -e的时候,控制台输出“crontab: installing new crontab”,表示任务添加成…...

06在IDEA中创建Java和Web工程,了解不同工程下的类路径,在IDEA中执行Maven命令
创建Java/Web模块 类路径的概述 IDEA中普通java项目中类路径的开始就是以src目录开始的路径,编译后的字节码文件和配置文件最终都会放在out目录下 Maven生成的目录结构中src/main目录下的java和resources目录都可以看作类路径的开始,编译后的字节码文件或资源文件会放在targ…...

自定义redission装配和集成分布式开源限流业务组件ratelimiter-spring-boot-starter的正确姿势
自定义redission装配和集成分布式开源限流业务组件ratelimiter-spring-boot-starter的正确姿势 文章目录 1.说明1.1 pom依赖1.2 引入redisson不引入redisson-spring-boot-starter依赖1.3 引入redisson-spring-boot-starter不引入redisson,启动类排除redisson-spring-boot-start…...
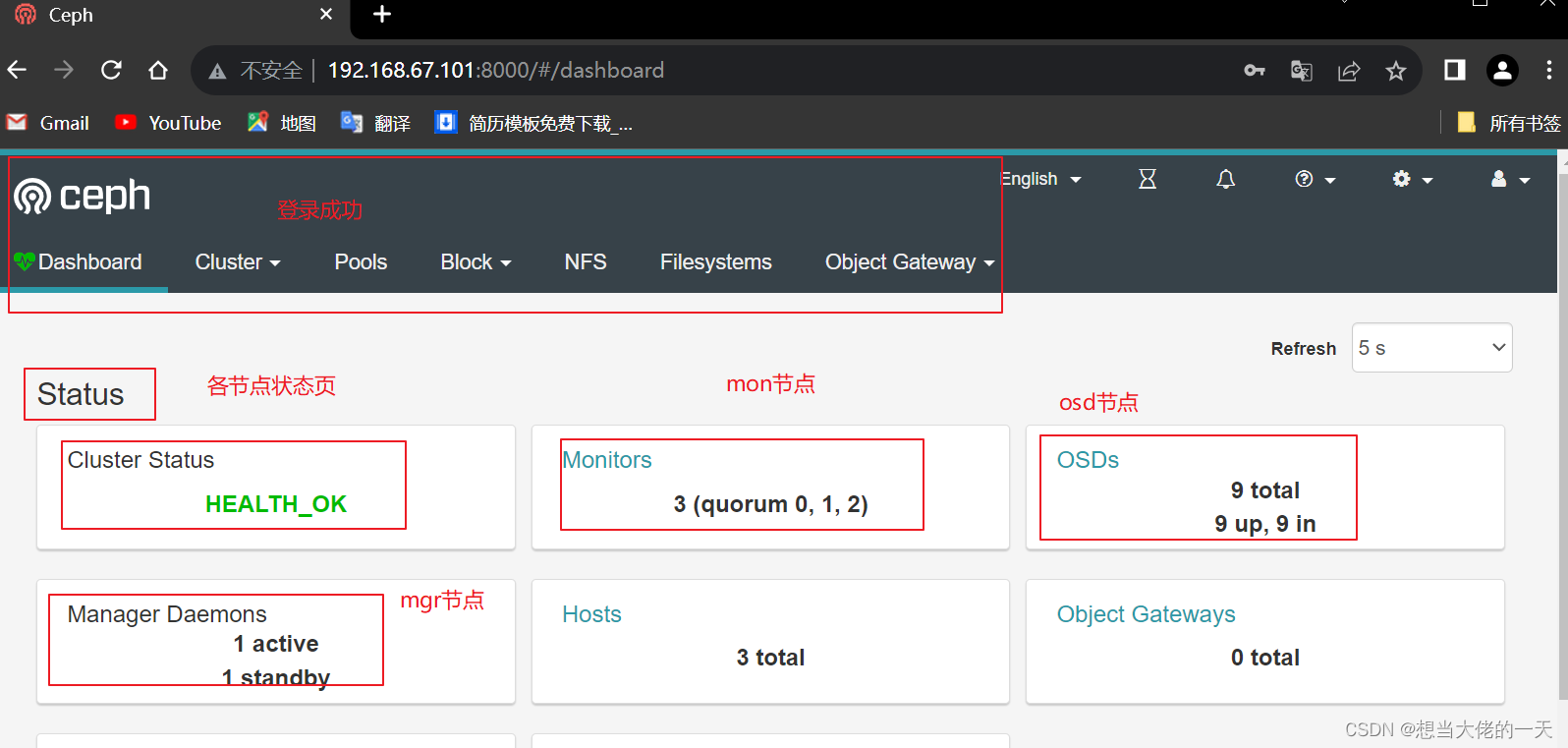
Ceph分布式存储的简单介绍与Ceph集群的部署搭建
文章目录 1. 存储的概述1.1 单机存储设备1.1.1 DAS(直接附加存储)1.1.2 NAS(网络附加存储)1.1.3 SAN(存储区域网络) 1.2 单机存储的缺陷1.3 分布式存储(软件定义的存储 SDS)1.4 分布…...

【环境搭建】linux docker安装nexus3
1、shell输入 docker run -dti \--nethost \--namenexus3 \--privilegedtrue \--restartalways \--ulimit nofile655350 \--ulimit memlock-1 \--memory1G \--memory-swap-1 \-e INSTALL4J_ADD_VM_PARAMS"-Xms512m -Xmx512m -XX:MaxDirectMemorySize1g" \-v /etc/lo…...

Java多线程下载文件
JVM是支持多线程程序的,当程序需要同时执行两个或多个任务,实现一些需要等待的任务时,如用户输入、文件读写、网络操作、搜索等多线程程序比单线程程序更具优势,可充分利用CPU资源,完成时间更短,提高应用程…...

oracle 同一张表同时insert多条数据 mysql 同一张表同时insert多条数据
oracle 同一张表同时insert多条数据 在Oracle数据库中,你可以使用INSERT ALL语句同时向同一张表插入多条数据。INSERT ALL语句允许你一次执行多个插入操作,可以提高插入的效率和速度。 以下是使用INSERT ALL语句插入多条数据的示例: INSERT…...
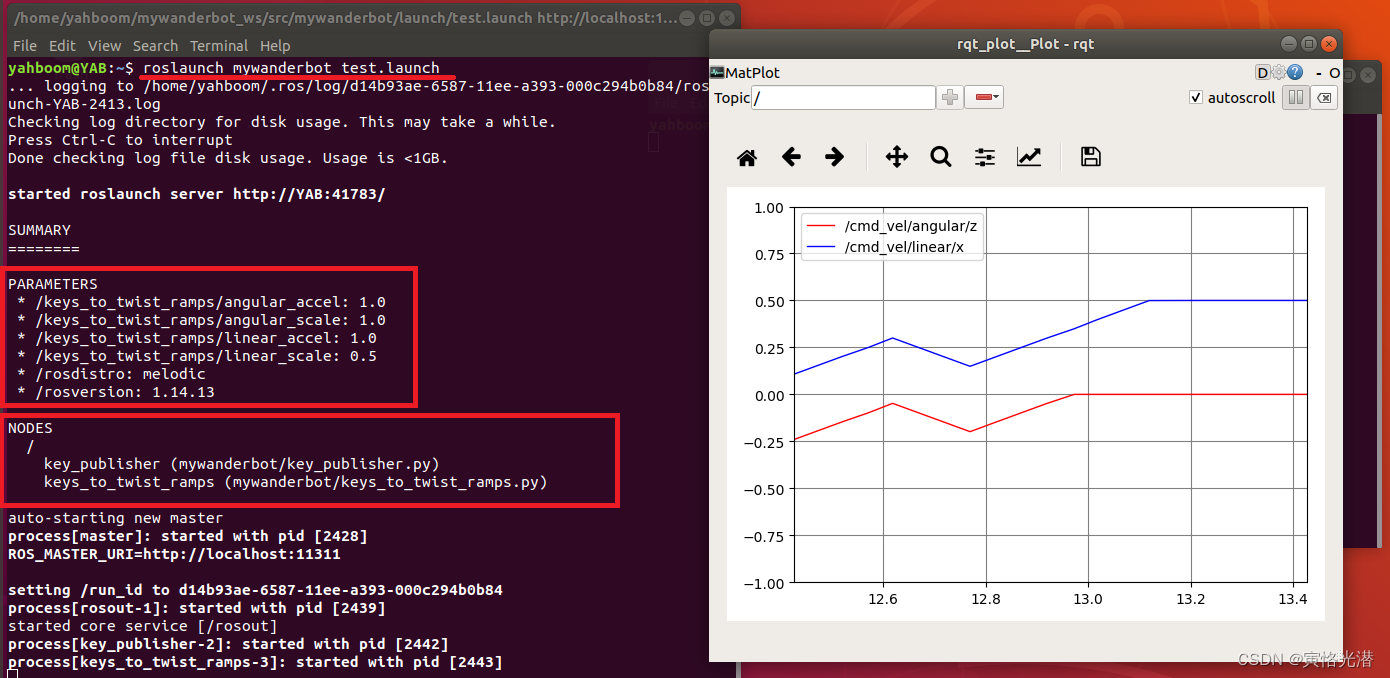
ROS键盘遥控机器人,通过参数服务器指定速度
1、引言 在上节的驱动机器人,我们知道是cmd_vel话题发布一串Twist类型消息来控制,我们可以输入如下命令查看这个Twist的详细信息:rosmsg show geometry_msgs/Twist geometry_msgs/Vector3 linear float64 x float64 y float64 z geome…...

具有快表的地址变换机构
1.快表(TLB) 快表,又称联想寄存器(TLB,translation lookaside buffer), 是一种访问速度比内存快很多的高速缓存(TLB不是内存! ), 用来存放最近访问的页表项的副本,可以加速地址变换的速度。 与…...

【使用python和flask建个人博客】修复侧边栏最新文章、最多阅读等链接不能打开的问题
自从上次因版本兼容问题修改过部分代码之后,好长时间没光顾woniunote这个个人博客模块了,最近发文章的时候发现侧边栏的文章打不开,定位了bug,并进行了修复。 <div class="col-12 side"><div class="tip" align...
ShareX使用说明——优秀的录屏软件
ShareX初识 ShareX 是一个自由及开放源代码的截图录像软件,目前仅支持Windows系统。 项目源代码在GitHub平台上发布, 软件可以在Microsoft商店和Steam上下载。 ShareX is a free and open source program that lets you capture or record any area of y…...
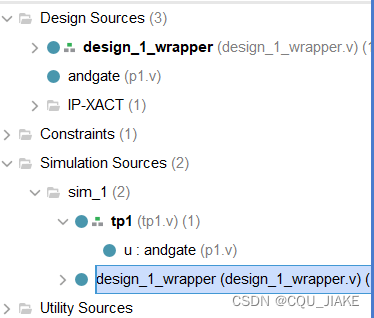
10.14~10.15verilog操作流程与Block Design
后面的那个是延时精度 verilog文件结构 文件名称与写的模板没有关系,这个文件名为P1,但模板名为andgate 但是如果是仿真文件,就需要开头的模板名和仿真文件名相同 .v是源文件,设计文件 .v在设计与sim里都有,静态共享࿰…...

小解C语言文件编译过程【linux】
小解C语言文件编译过程【linux】 库动态库静态库 C语言文件 程序编译过程整体预处理编译汇编链接动态链接静态链接两种方法对比 库 看到标题是文件编译过程 但是开头却是库,这可不是挂羊头卖狗肉,而是因为库也是代码不可缺少的一部分,并且在…...

[Python]黑色背景白色块滑动视频
黑色背景白色块滑动视频,单帧效果如下: 配置参数 1920 1080 400 400 300 60 1920x1080.avi import numpy as np import cv2 as cv import os import syswidth 1920 height 1080 rect_szx 400 rect_szy 300 sz_y_init 400 fps 24width int(sys.a…...

【linux kernel】对linux内核设备的注册机制和查找机制分析
文章目录 1、简介2、device_initialize分析3、device_add分析4、总结 🔺【linux内核系列文章】 👉对一些文章内容进行了勘误,本系列文章长期不定时更新,希望能分享出优质的文章! 1、《linux内核数据结构分析之哈希表》…...
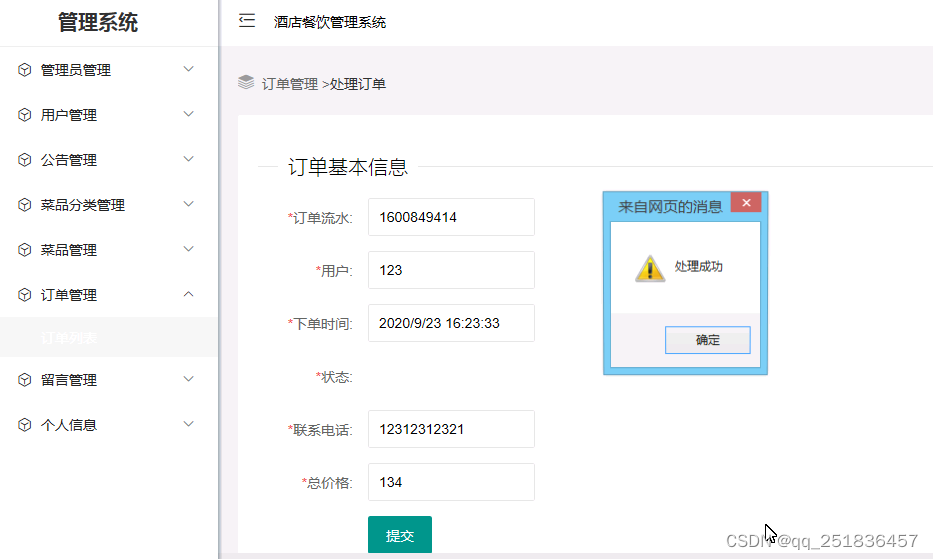
asp.net酒店餐饮管理系统VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio
一、源码特点 asp.net酒店餐饮管理系统是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为sqlserver2008,使用c#语言 开发 ASP.NE 酒店餐饮管理系统 二、功能…...
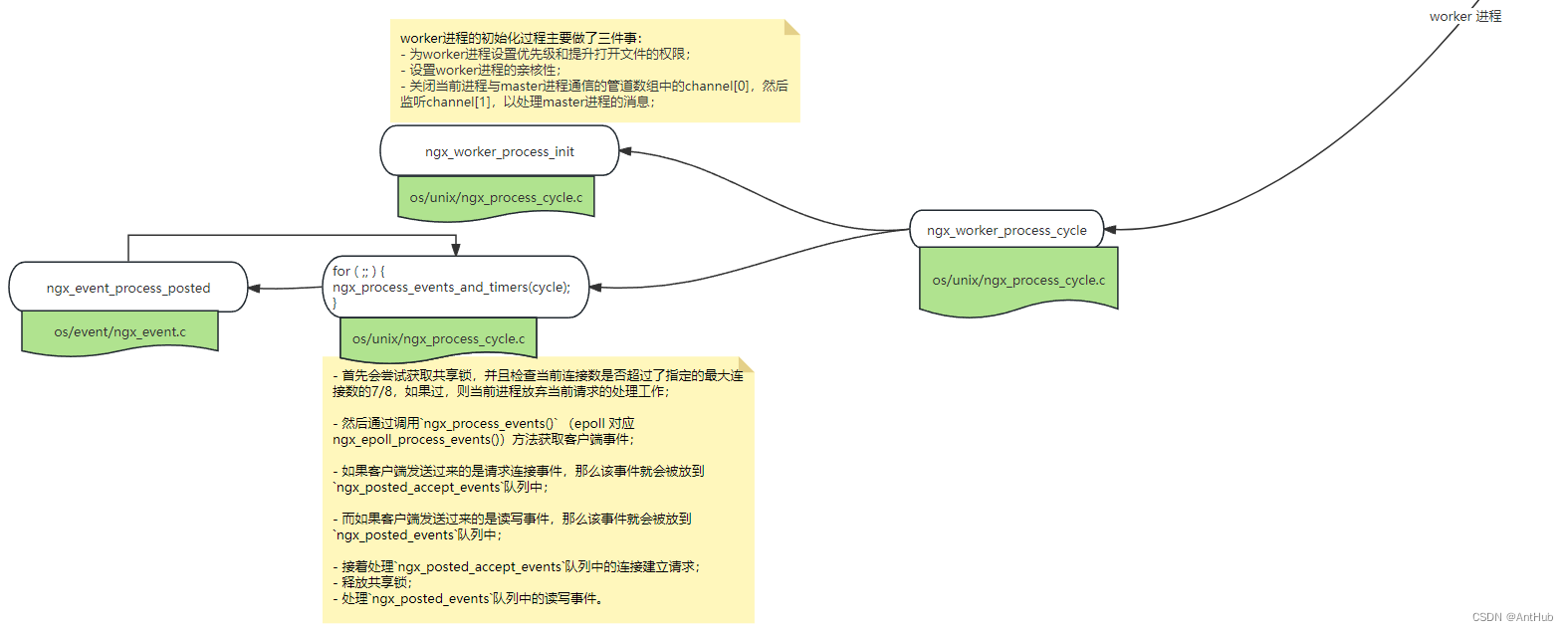
38_Nginx 启动流程
文章目录 src/core/nginx.cint ngx_cdecl main(int argc, char *const *argv) {ngx_buf_t *b;...
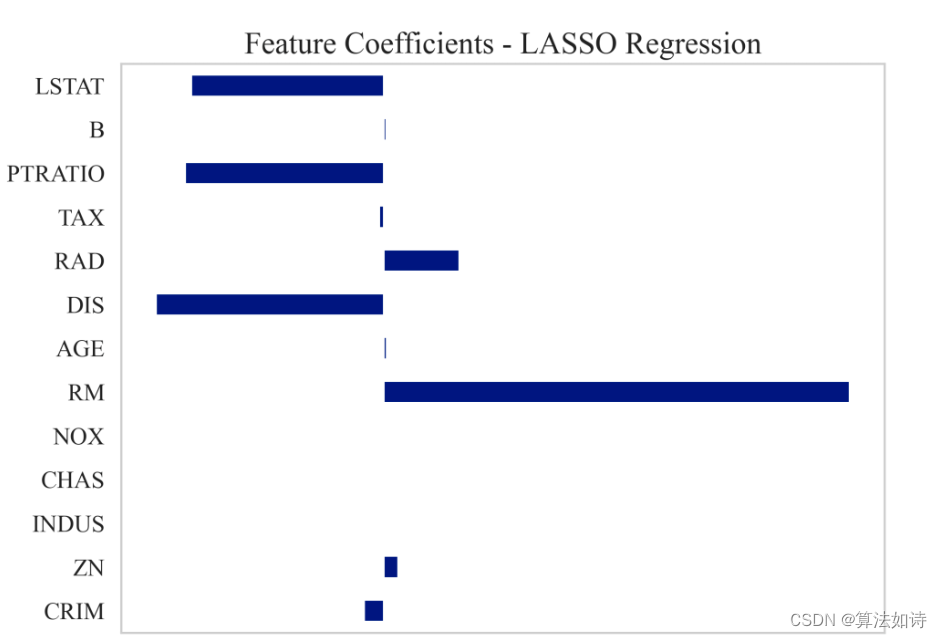
数据特征选择 | Lasso特征选择(Python)
文章目录 效果一览文章概述源码设计小结效果一览 文章概述 Lasso算法是一种经典的线性回归算法,被广泛应用于特征选择和降维问题。相较于传统的线性回归算法,Lasso算法能够在保持预测准确性的同时,自动筛选出对目标变量影响较大的特征变量,从而达到降低模型复杂度、提高泛化…...

最小覆盖子串[困难]
优质博文:IT-BLOG-CN 一、题目 给你一个字符串s、一个字符串t。返回s中涵盖t所有字符的最小子串。如果s中不存在涵盖t所有字符的子串,则返回空字符串"" 。 对于t中重复字符,我们寻找的子字符串中该字符数量必须不少于t中该字符数量…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
