论文笔记[156]PARAFAC. tutorial and applications
原文下载:https://www.sciencedirect.com/science/article/abs/pii/S0169743997000324
摘要
本文介绍了PARAFAC的多维分解方法及其在化学计量学中的应用。PARAFAC是PCA对高阶数组的推广,但该方法的一些特性与普通的二维情况截然不同。例如,可以从多维光谱数据(multi-way spectral data)中恢复出纯光谱(pure spectra)。
1 介绍
以交叉方式测量变量,结果的集合为多维数据。
PARAFAC以及二路PCA等方法都是多线性或双线性分解方法,它们将数组分解成分数和负载[16](loadings)的集合,希望以比原始数据数组更精简的形式描述数据。
主成分分析模型可以被认为是最复杂和最灵活的模型,而PARAFAC是最简单和最受限制的模型。
结构越多,拟合越差,模型越简单。使用多维方法不是为了获得更好的拟合,而是为了获得更充分、更稳健和可解释的模型。
对于组分数为F的I×J×K数组,平行因子模型含有F(I+J+K)个参数。
PARAFAC的一个非常令人讨厌的特性是计算模型所需的时间很长。所使用的算法通常基于交替最小二乘法(ALS),ALS的初始化使用随机值或基于广义特征值问题的直接三线性(trilinear)分解。
在下文中,为了简单起见,讨论将仅限于三维(three-way)数据,但大多数结果对任何(更高)阶的数据和模型都有效。
2 术语
标量:小写斜体
矢量:粗体小写
二维矩阵:粗体大写
三维数组:带下划线的粗体大写字母
xijk:X的第ijk个元素
模式(mode)、way和顺序(order)这三个术语或多或少可以互换使用。
术语因子(factor)和组分(component)之间没有区别。
3 模型
数据被分解为三线性分量(三元组,triads),每个分量由一个分数向量和两个负载向量组成。在三维中,通常不区分分数和负载(,因为分数和负载在数学上是同等对待的)。
三维数组的平行因子模型由三个负载矩阵A、B、C组成(其中的元素分别表示为aif、bjf、ckf),建立三线性模型以最小化模型中的残差eijk。三维数组的元素可由负载矩阵的元素与残差计算得到,公式如下:
x i j k = ∑ f = 1 F a i f b j f c k f + e i j k ( 1 ) x_{ijk}=\sum_{f=1}^{F}a_{if}b_{jf}c_{kf}\;+e_{ijk} (1) xijk=f=1∑Faifbjfckf+eijk(1)
图1为公式(1)在二组分情况下的计算示意图。
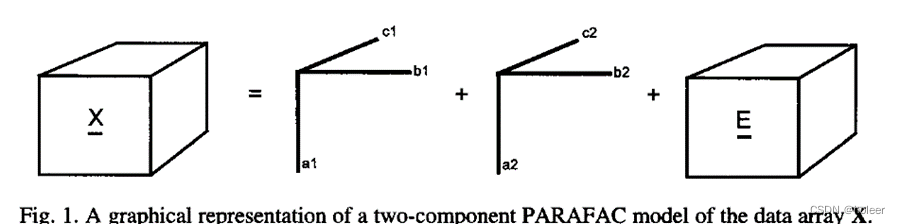
该模型也可记为: X ‾ = ∑ f = 1 F a f ⨂ b f ⨂ c f \underline{X}=\sum_{f=1}^{F}a_f\bigotimes b_f\bigotimes c_f X=f=1∑Faf⨂bf⨂cf
其中af、bf、cf分别为矩阵A、B、C的第f列。
3.1 唯一性
PARAFAC模型的一个明显优点是解的唯一性。如果数据确实是三线性的,使用了正确数量的分量并且信噪比合适,就能得到真正的潜在光谱。
3.2 多维数组的秩(rank)
秩为1的矩阵可以写成2个向量(分数和负载向量)的外积。这样的组成部分被称为二元组。
三元组是二元组的三线性等价物,即三线性(PARAFAC)分量,是3个向量的积。
4 实现
4.1 交替最小二乘法(Alternating least squares)
PARAFAC模型的解可以通过该方法找到,方法是依次假设两种已知模式下的载荷,然后估计最后一种模式的未知参数集。这也是最初提出的对模型进行估计的方式。
PARAFAC ALS算法的流程:
(0)确定组分数F
(1)初始化B和C
(2)通过最小二乘回归,从X, B, C中估计A
(3)用同样的方法估计B
(4)用同样的方法估计C
(5)从步骤(2)开始往下执行,直到收敛。
ALS算法将在每次迭代中改善模型的拟合。如果算法收敛到全局最小值,则找到模型的最小二乘解。
ALS的优点:确保每次迭代都能优化解;ALS的主要缺点:模型估计时间长,当变量数量很多时,有时需要数百到数千次迭代才能收敛。
6 评估解
6.2 杠杆和残差
杠杆和残差可用于影响和残差分析。
6.3 组分数
提取太多的分量不仅意味着噪声被越来越多地建模,而且真实因素被更多(相关)的分量建模。
确定组分数的主要方法有三种:(1)分半实验,(2)判断残差,(3)与建模数据的外部知识进行比较。
[19]主张使用分半实验。其想法是将数据分为两半,然后在这两半上创建PARAFAC模型。通常情况下,应该以具有足够数量的自变量/样本(independent variables/samples)的模式来分割数据。
9 应用II:稀疏荧光数据的唯一分解
9.1 数据
这个问题是PARAFAC使用非负约束获得唯一分解的一个示例。
样品:含有不同量的酪氨酸、色氨酸和苯丙氨酸的2个样品。
因此,要分解的数组是2×51×201。
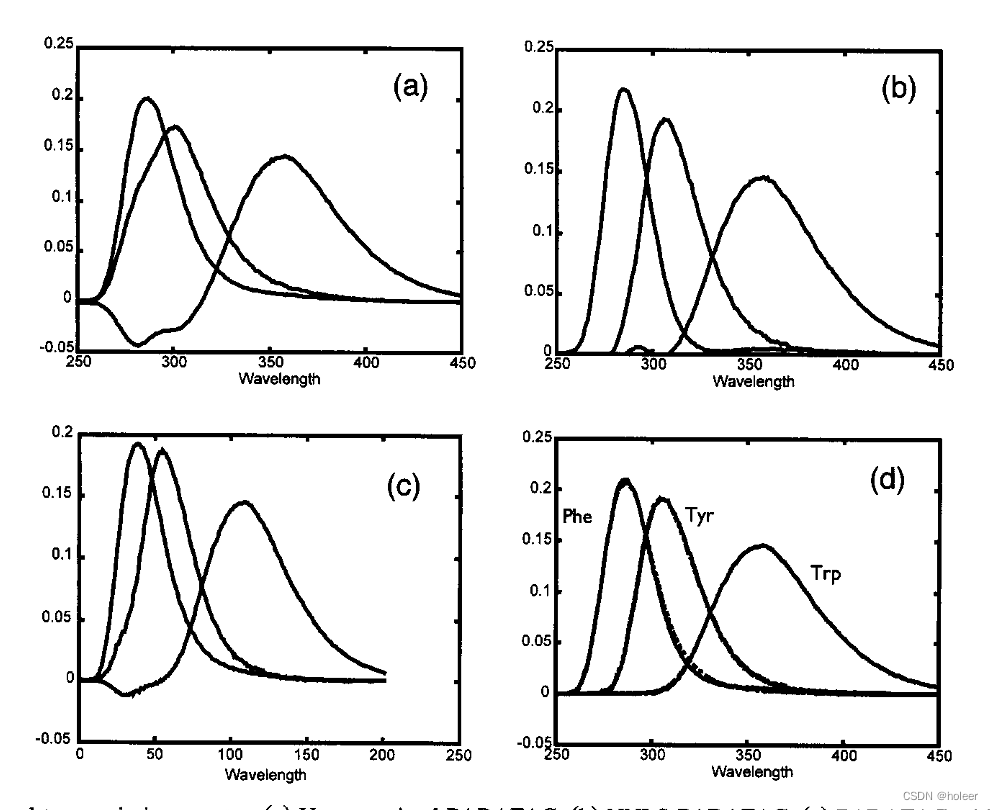
图10d中的估计负载(实线)与纯谱(虚线,注意区分)一起显示。估计的载荷量现在与纯光谱非常相似。
样本模式的负载是估计的分析物的浓度。
在多线性分解中应该避免瑞利散射,有三种方法可以做到这一点:(iii)测量空白,并从样品测量值中减去该测量值。在这个实验中,最初没有采取任何措施来消除瑞利散射。
9.2 结果与讨论
- 三组分PARAFAC溶液的发射负载如图10a所示。从中可以看出,与色氨酸相对应的光谱具有大的负区域。得出的结论是,由于变化性小(两个样品),分解很困难。由于我们知道荧光光谱和浓度应该是正的,所以很自然地将PARAFAC 负载限制在正值 。
- 在图10b中,使用非负性约束显示了估计的发射负荷。估计的光谱与分析物的纯光谱非常相似,但对于色氨酸,由于非多重线性瑞利散射,在300mn以下有一个小峰。
- 为了避免这种情况,试图将受瑞利散射影响的所有变量设置为缺失值,然后估计相应的PARAFAC模型,结果如图10c所示。
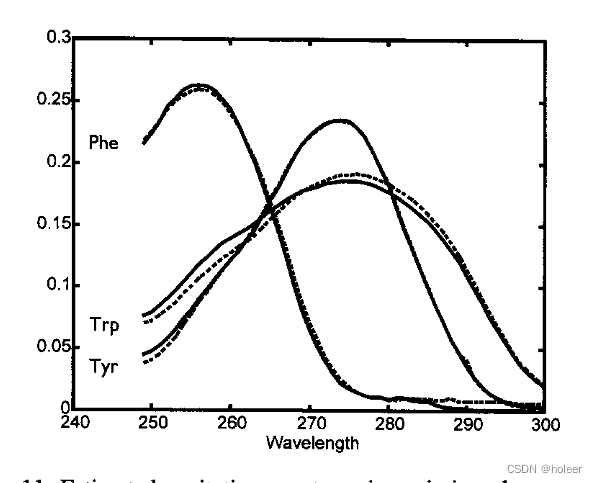
- 显然,仅凭这一点不足以确保色氨酸光谱具有良好的曲线分辨率。将缺失元素方法与非负约束相结合,有助于模型关注图中数据的正确方面。在图10d中,估计的发射负载与纯光谱一起显示。估计的载荷现在与纯光谱非常相似。估计的激发光谱如图11所示。
相关文章:

论文笔记[156]PARAFAC. tutorial and applications
原文下载:https://www.sciencedirect.com/science/article/abs/pii/S0169743997000324 摘要 本文介绍了PARAFAC的多维分解方法及其在化学计量学中的应用。PARAFAC是PCA对高阶数组的推广,但该方法的一些特性与普通的二维情况截然不同。例如,…...

AKKA.Net 的使用 来自CHATGPT
请用C# 语言实现一个自动化设备 流水线调度模型,流水线各个环节需要并行执行: 下面是一个使用C#语言实现自动化设备流水线调度模型的简单示例。该示例使用并发编程库System.Threading.Tasks来实现流水线各个环节的并行执行。 csharp using System; usi…...

网络安全—小白学习笔记
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟入…...

OpenRemote: Java 开源 IoT 物联网开发平台,匹配智慧城市、智能家居、能源管理
OpenRemote 是一个直观、用户友好的基于Java语言的开源 IoT 物联网设备管理平台,它包括从连接设备到构建应用程序和特定领域的智能应用程序的所有功能和特性。通过OpenRemote物联网平台,用户可以收集和处理来自不同设备的传感器数据,适用于智…...
GO-unioffice实现word编辑
导包 import ("fmt""log""os""time""github.com/unidoc/unioffice/common/license""github.com/unidoc/unioffice/document" ) 创建word文件 func CreateFile(name string) {filename : name ".docx&quo…...

SpringMVC的拦截器(Interceptor)
拦截器简介 SpringMVC的拦截器Interceptor,主要是对Controller资源访问时进行拦截的基本操作的技术,当然拦截后可以进行权限控制,功能增强等都是可以的。拦截器类似于JavaWeb开发中的Filter,他们之间的区别如下图所示 Filter技术…...
【git】gitlab常用命令
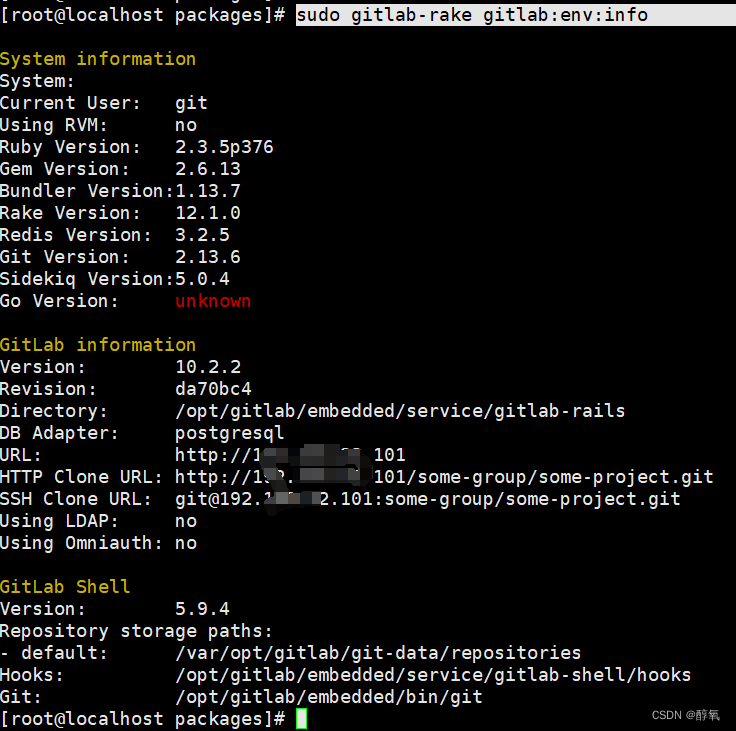
gitlab官网 官网:官网 中文官网:中文官网 默认的gitlab安装目录 /opt/gitlab/bin 启动 gitlab-ctl start 查看状态 gitlab-ctl status 停止 gitlab-ctl stop 重启GitLab gitlab-ctl restart 查看gitlab的配置文件 配置的路径是:/…...
解读下SWD协议以及其应用
SWD协议原理 SWD(Serial Wire Debug)协议是一种用于ARM Cortex微控制器的调试接口协议。它定义了主机计算机与目标设备之间通过SWD线进行通信的格式和规范。 SWD协议使用两根线进行通信:SWDIO(Serial Wire Debug I/O)…...

基于单目的光流法测速
目录 1.简介 2.代码实现 1.简介 基于单目的光流法是一种常见的计算机视觉技术,用于估计图像序列中物体的运动速度。它通过分析连续帧之间的像素变化来推断物体在图像中的移动情况。 背景: 光流法是计算机视觉领域中最早的运动估计方法之一,…...
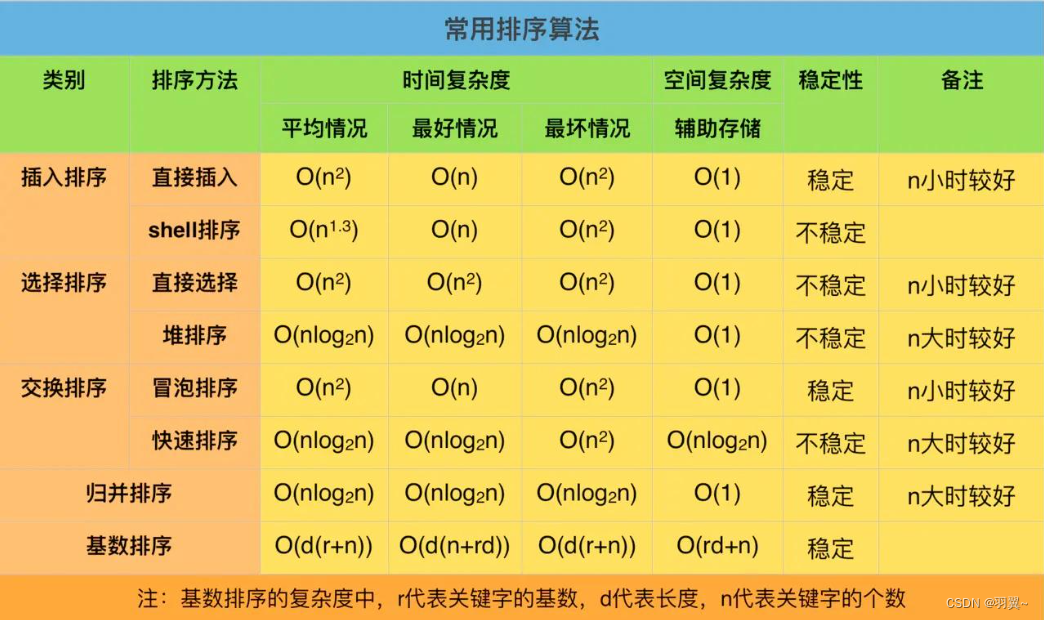
排序-算法
文章目录 一、排序的概念及引用1.1 排序概念1.2 排序运用1.3 常见排序算法 二、常见排序算法的实现2.1 插入排序2.1.1 基本思想2.1.2 直接插入排序2.1.3 希尔排序 2.2 选择排序2.2.1 基本思想2.2.2 直接选择排序2.2.3 堆排序 2.3 交换排序2.3.1 冒泡排序2.3.2 快速排序2.3.3 快…...
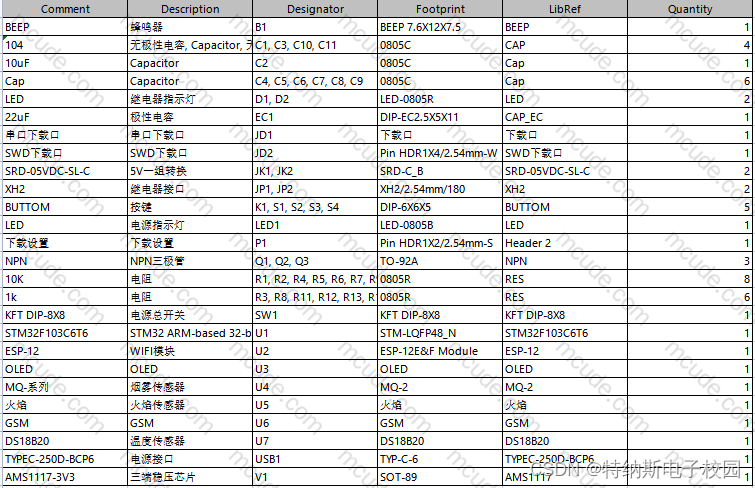
【特纳斯电子】基于单片机的火灾监测报警系统-实物设计
视频及资料链接:基于单片机的火灾监测报警系统-实物设计 - 电子校园网 (mcude.com) 编号: T0152203M-SW 设计简介: 本设计是基于单片机的火灾监测报警系统,主要实现以下功能: 1.通过OLED显示温度、烟雾、是否有火…...
网络安全就业形势怎么样?
泻药,以下都是我本人的肺腑之言,是答主深耕职场多年,转战数家公司总结周围朋友的从业经验才总结出来的行业真相,真心希望帮助到还没有步入职场的大家,尤其是24届的应届毕业生,多掌握些就业信息就能少走一些…...
【Golang】Go的并发和并行性解释。谁说Go不是并行语言?
偶然发现百度上有很多"师出同门"的"go是并发语言,而不是并行语言"的说法。让我顿感奇怪,"并行"说白了就是对CPU多核的利用,这年头不能利用多核的编译语言还有的混?而且还混的这么好?并且…...
k8s-16 k8s调度
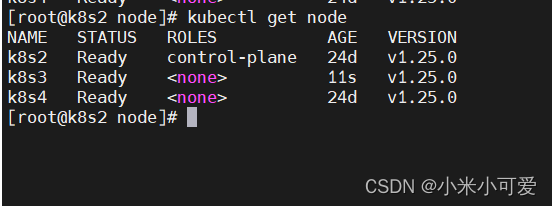
调度器通过 kubernetes 的 watch 机制来发现集群中新创建且尚未被调度到 Node上的 Pod。调度器会将发现的每一个未调度的 Pod 调度到一个合适的 Node 上来运行。 kube-scheduler 是 Kubernetes 集群的默认调度器,并且是集群控制面的一部分如果你真的希望或者有这方面…...
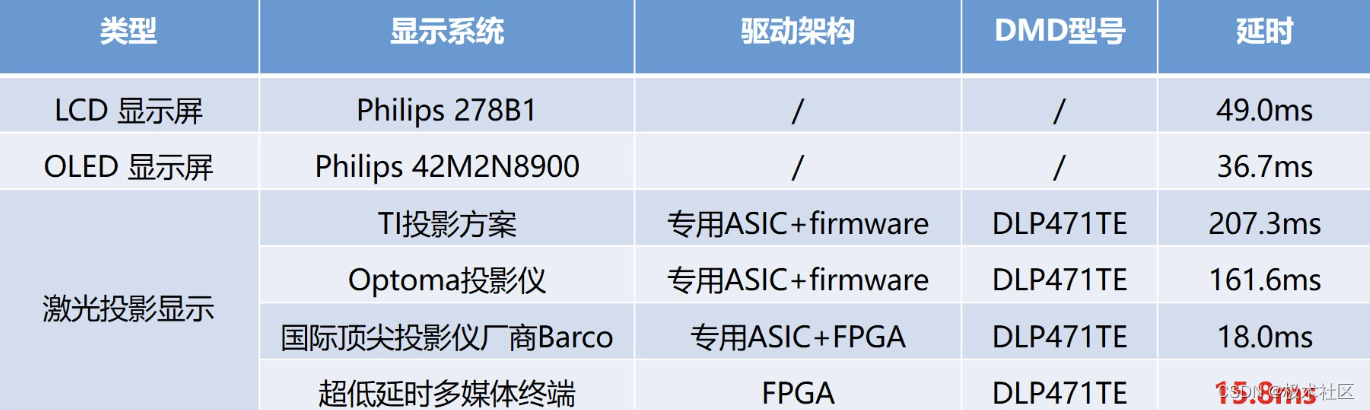
【2023研电赛】全国技术竞赛一等奖:基于FPGA的超低时延激光多媒体终端
该作品参与极术社区组织的研电赛作品征集活动,欢迎同学们投稿,获取作品传播推广,并有丰富礼品哦~ 基于FPGA的超低时延激光多媒体终端 参赛单位:华东师范大学 指导老师:刁盛锡 参赛队员:王泽宇 谢祖炜 秦子淇…...
Annoy vs Milvus:哪个向量数据库更适合您的AI应用?知其然知其所以然
1. Annoy vs Milvus简介 Annoy 和 Milvus 都是用于向量索引和相似度搜索的开源库,它们可以高效地处理大规模的向量数据。 Annoy(Approximate Nearest Neighbors Oh Yeah): Annoy 是一种近似最近邻搜索算法,它通过构…...
)
android 13.0 SystemUI导航栏添加虚拟按键功能(一)
1.概述 在13.0的系统产品开发中,在系统SystemUI的原生系统中默认只有三键导航,想添加其他虚拟按键就需要先在构建导航栏的相关布局中分析结构,然后添加相关的图标xml就可以了,然后添加对应的点击事件,就可以了,接下来先分析第一步关于导航栏的相关布局情况 然后实现功能 …...

内存管理-分页、虚拟地址、虚拟内容、页面置换算法
文章目录 一、5W2H角度分析内存管理What是内存管理Why需要内存管理Who使用内存管理Where内存管理应用When需要内存管理How内存管理工作How much内存管理的成本 二、分页什么是分页分页的原理分页的优缺点分页的应用 三、虚拟地址什么是虚拟地址虚拟地址的作用虚拟地址的转换虚拟…...
【C++入门】命名空间详解(从零开始,冲击蓝桥杯)
C入门 命名空间 南喵小鸡汤程序员可以让步,却不可以退缩,可以羞涩,却不可以软弱,总之,程序员必须是勇敢的。一 . 命名空间的介绍二.命名空间的实际应用1.为什么要有命名空间我们在使用变量时,通常会为他定义一个名字,在…...
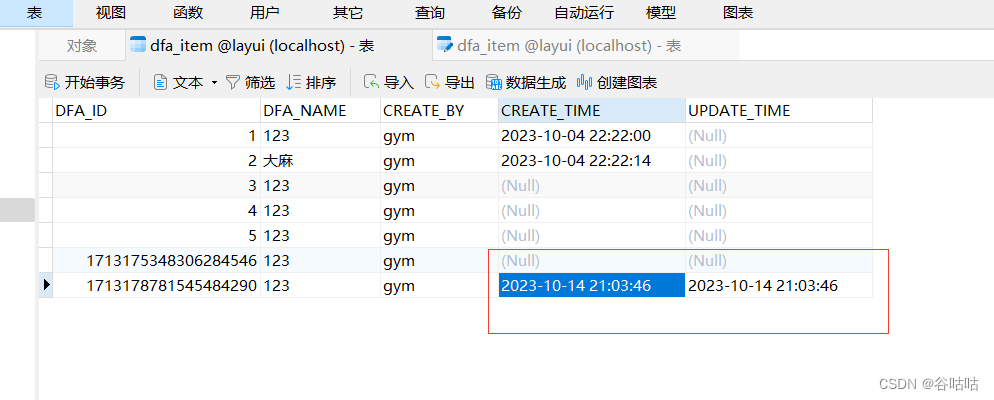
通过代码MyBatis-plus实现对表中createTime和updateTime进行自动更新
通过代码MyBatis-plus实现对表中createTime和updateTime进行自动更新 实现这样的效果可以在数据库中设置,但是我们一般建议在代码里实现, 但是总不能每次insert和update的时候都手写new当前时间 因此推荐使用mybatis-plus 1导入依赖 <dependency&g…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
