代码随想录Day20 回溯算法 LeetCode77 组合问题
以下内容更详细解释来自于:代码随想录 (programmercarl.com)
1.回溯算法理论基础
回溯法也叫回溯搜索法,是搜索法的一种,我们之前在二叉树中也经常使用到回溯来解决问题,其实有递归就有回溯,有的时候回溯隐藏在递归之下,我们不容易发觉,今天我们来详细介绍一下什么是回溯,它能解决哪些问题.
回溯法效率
回溯法的效率是不高的,回溯的本质是穷举,因为有些问题能用回溯法解决出来就不错了,别无他法,只能使用这个暴力方法
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
提供一个八皇后小游戏hhh:【死亡8皇后】小游戏_游戏规则玩法,高分攻略-2345小游戏
理解回溯法的方式
不要光靠脑子想,要将这种回溯具象化,想象成树形结构,任何回溯法解决的问题都可以转化为树形结构来解决问题.
因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度.
递归就要有终止条件,所以必然是一棵高度有限的树(N叉树).
回溯法代码模板(伪代码)
首先是函数参数和返回值
一般无需返回值,参数很多,一般边写边定,函数名一般定为backtracking
void backtracking(参数)终止条件
我们说可以将回溯算法想像成一个树形结构,那么我们就一定有终止条件,一般到达终止条件(叶子结点),也就是我们收获答案的时候,相关为伪代码如下
if (终止条件) {存放结果;return; }回溯搜索的遍历过程
上文中我们说回溯的树的宽度取决于元素个数,回溯深度取决于递归深度,如图所示
回溯算法遍历的伪代码如下
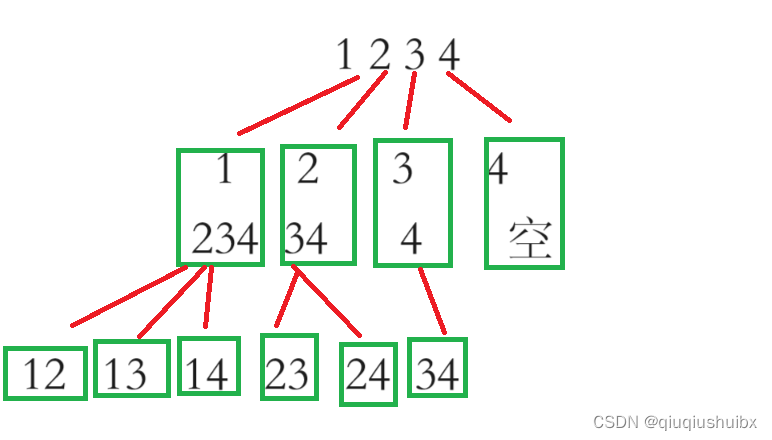
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果 }注意这里的撤销,假设我们要求1234中size为2的组合,有 12 13....这里假设我们第一个节点是12,这里我们要得到13就得将2pop出去,也就是我们回溯撤销的过程.
回溯模板(全)
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果} }
2.经典例题 :LeetCode T77 组合问题


题目链接:77. 组合 - 力扣(LeetCode)
题目思路:
我们说递归有三部曲,这里我们回溯也有三部曲,这里我们首先定义一个path变量,来存放我们每条路径上的结果,因为这里我们可以将回溯过程想象成n叉树,所以叶子结点的结果也可以想象成路径的结果,然后定义一个result数组来存放所有路径的集合,这里我们定义为全局变量,下面函数实现中直接操作即可.
List<Integer> path = new ArrayList<>(); List<List<Integer>> result = new ArrayList<>();
我们以1234中排列2个数字,即n = 4,k = 2为例,画出如下图
回溯三部曲
1.确定函数参数和返回值
这里n和k肯定是需要的,还有我们需要一个参数就是从哪里开始,于是我们定义一个变量startIndex来记录每次递归开始的逻辑,比如第一次从1开始,第二次从2开始
public void backtracking(int n, int k,int startIndex)2.确定终止条件
这里的终止条也是收割结果的时候,我们发现树的叶子节点就是我们所要的结果,我们写出如下代码
//终止条件if(path.size() == k){result.add(new ArrayList<>(path));return;}3.确定一次递归(回溯)过程
这里我们按照上文所说就是我们for循环该登场了,这个时候我们的循环就得从startIndex开始到n结束,里面需要做的事情就是path.add元素,再进行backtracking,最后得pop元素进行一次回溯的过程,这里我们可以想象假设上面这个1234的例子,这里我收集了12这个例子,我想收获13这个结果是不是得将2弹出再将3进行添加呀,下面是代码演示
//for循环for(int i = startIndex;i<=n;i++){path.add(i);backtracking(n,k,i+1);path.remove(path.size()-1);}
题目代码:
class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> result = new ArrayList<>();public List<List<Integer>> combine(int n, int k) {backtracking(n,k,1);return result;}public void backtracking(int n, int k,int startIndex){//终止条件if(path.size() == k){result.add(new ArrayList<>(path));return;}//for循环for(int i = startIndex;i<=n;i++){path.add(i);backtracking(n,k,i+1);path.remove(path.size()-1);}}
}代码优化
还是以上面1234举例,这里我们可以进行一次剪枝,假设我们n = 4,k = 4我们就会发现startIndex取2后面的值就毫无意义了,这里我们就可以对这种情况剪枝,如果后面的元素不足以我构成我们的一次正确的结果,就不要去遍历它了
优化过程如下:
已经选择的元素个数:path.size();
还需要的元素个数为: k - path.size();
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2,这里都是合理的
只需修改一下for循环的区间即可
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++)
相关文章:
代码随想录Day20 回溯算法 LeetCode77 组合问题
以下内容更详细解释来自于:代码随想录 (programmercarl.com) 1.回溯算法理论基础 回溯法也叫回溯搜索法,是搜索法的一种,我们之前在二叉树中也经常使用到回溯来解决问题,其实有递归就有回溯,有的时候回溯隐藏在递归之下,我们不容易发觉,今天我们来详细介绍一下什么是回溯,它能…...
免费获取天气预报的API接口(Json格式)
免费获取天气预报的API接口(Json格式) 1、接口地址2、城市代码 1、接口地址 当需要获取某个城市天气数据json时候,需要传入一个城市代码编码作为入参,地址: http://t.weather.itboy.net/api/weather/city/xxxxx &…...

安卓程序执行入口
Android程序执行入口 Android应用程序的执行入口是在一个特定的 Java 类中,通常是 MainActivity 或 SplashActivity,具体取决于应用的设计和结构。 Android应用程序的执行入口通常通过以下方式进行定义: 在 AndroidManifest.xml 文件中&am…...
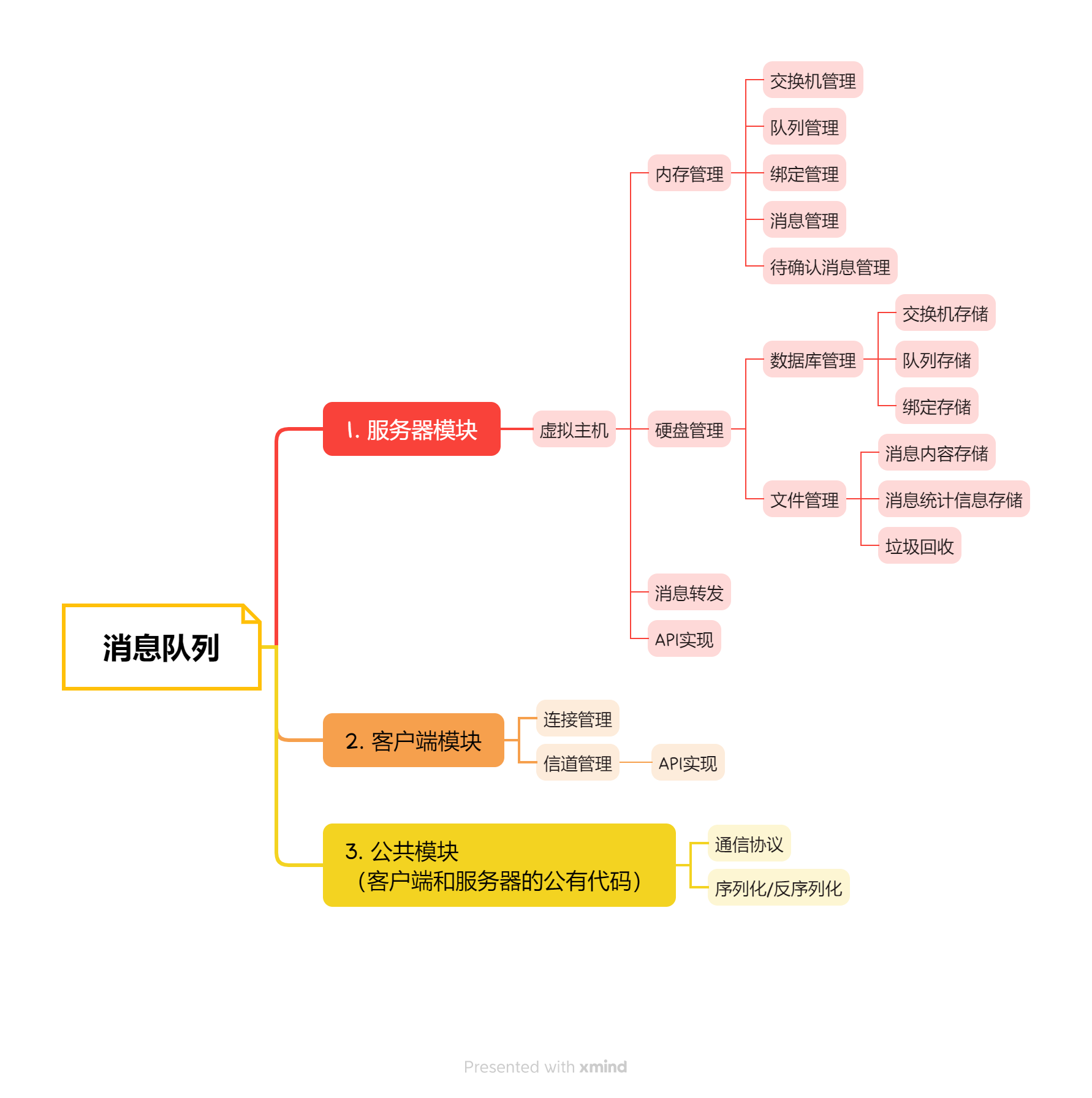
消息队列(中间件)
通信协议: 为了实现客户端和服务器之间的通信来完成的逻辑,基于TCP实现的自定义应用层协议。通过这个协议,完成客户端–服务器远程方法调用。 序列化/反序列化: 通过网络传输对象把对象存储到硬盘上。 序列化:把对象转化为二进制的…...

Java|学习|异常
1.异常 1.1 异常 1.1.1 概述 异常:就是程序出现了不正常的情况。 Error:严重问题,不需要处理。 Exception:称为异常类,它表示程序本身可以处理的问题。 RuntimeException:在编译器不检查,出…...

nextjs项目修改启动端口号,以及开发启动后自动打开浏览器
next版本:13.5.4 一、修改端口 在package.json文件当中修改启动命令 "scripts": {"dev": "next dev -p 3100","build": "next build","start": "next start","lint": "ne…...
微服务架构 | 超时管理
INDEX LSA 级别与全年停机时间速查表LSA 级别实战TP 性能超时时间设计原则 LSA 级别与全年停机时间速查表 计算公式:60 * 60 * 24 * 365 * (1-LSA) 31,536,000 * (1-LSA) 系统级别LSA级别全年停机时间099.999%5分钟099.99%52分钟199.9%8.8小时299%3.65 天 LSA…...

Qt 样式表大全整理
【QT】史上最全最详细的QSS样式表用法及用例说明_qt样式表使用大全_半醒半醉日复日,花落花开年复年的博客-CSDN博客 QT样式表的使用_qt 设置按下 release hover 按钮样式表_create_right的博客-CSDN博客 QPushButton {border-image: url(:/Start_Stop.png); } QPu…...

k8s-10 cni 网络
k8s通过CNI接口接入其他网络插件来实现网络通讯。目前比较流行的插件有flannel,calico等。 CNI插件存放位置: # cat /etc/cni/net.d/10-flannel.conflist 插件使用的解决方案如下: 虚拟网桥,虚拟网卡,多个容器共用一个虚拟网卡进行通信。多路复用: Mac…...

IDEA中.gitignore配置不生效的解决方案
一、创建项目 二、执行以下Git命令 git rm -r --cached . git add . git commit -m "update .gitignore"...

SparkContext 与 SparkContext 之间的区别是什么
SparkContext 是 Spark 的入口点,它是所有 Spark 应用程序的主要接口,用于创建 RDD、累加器、广播变量等,并管理与 Spark 集群的连接。在一个 Spark 应用程序中只能有一个 SparkContext。 而 SparkSession 是 Spark 2.0 新增的 API࿰…...

lv8 嵌入式开发-网络编程开发 17 套接字属性设置
1 基本概念 设置套接字的选项对套接字进行控制除了设置选项外,还可以获取选项选项的概念相当于属性,所以套接字选项也可说是套接字属性有些选项(属性)只可获取,不可设置;有些选项既可设置也可获取 2 选项…...

VulnHub Alice
一、信息收集 发现开发了22、80 2.访问ip,右击查看源代码 发现需要利用X-Forwarded-For 火狐插件:X-Forwarded-For Header 挂上代理后: 出现以下页面: 先注册一个账户,然后再登录 发现有参数进行传参 发现传参&a…...

AUTOSAR组织发布20周年纪念册,东软睿驰NeuSAR列入成功案例
近日,AUTOSAR组织在成立20周年之际发布20周年官方纪念册(20th Anniversary Brochure),记录了AUTOSAR组织从成立到今天的故事、汽车行业当前和未来的发展以及AUTOSAR 伙伴关系和合作在重塑汽车方面的作用。东软睿驰提报的基于AUTOS…...

转行网络安全是否可行?
一、前言 其实很多的IT大佬之前也不是专门学计算机的,都是后期转行的。而且大学学什么专业,对后期的工作真的没有太大关系,这也是现在高校的教育现状。有80%的学生都是通过临时抱佛脚,考前冲刺拿到毕业证书的。下面就带大家详细分…...
netca_crypto.dll找不到怎么修复?详细解决办法和注意事项
当你在使用计算机时,突然出现了一个错误提示:“netca_crypto.dll 找不到”。不知道该如何解决这个问题?其实要解决是非常的简单的,今天我们将为你提供几种修复 netca_crypto.dll 找不到的解决方法和一些注意事项。在深入探讨修复方…...

axios的请求中断和请求重试
请求中断 场景:1、假如一个页面接口太多、或者当前网络太卡顿、这个时候跳往其他路由,当前页面可以做的就是把请求中断掉(优化)2、假如当前接口调取了第一页数据,又调去了第二页的数据,当我们调取第二页数…...
视频怎么压缩?视频太大这样处理变小
在当今时代,视频已经成为了我们日常生活中不可或缺的一部分,然而,视频文件往往非常大,给我们的存储和传输带来了很大的不便,那么,如何有效地压缩视频呢? 一、使用压缩软件 首先我们给大家分享一…...
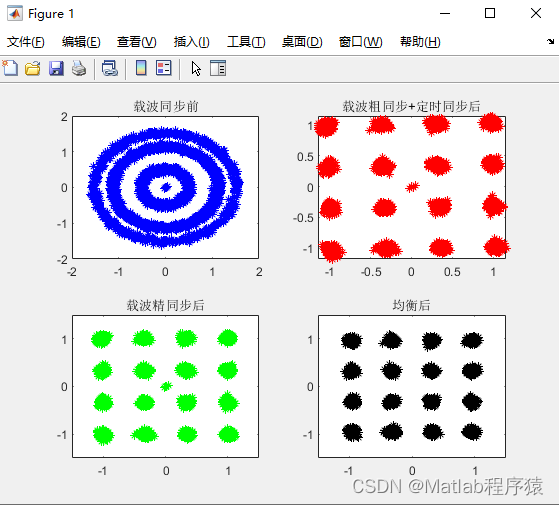
【MATLAB源码-第48期】基于matlab的16QAM信号盲解调仿真。
操作环境: MATLAB 2022a 1、算法描述 16QAM (16个象限幅度调制) 是一种广泛使用的数字调制技术。在无线和有线通信系统中,为了在固定的带宽内发送更多的信息,高阶调制如16QAM被使用。下面是16QAM盲解调的基本步骤、优缺点及应用场景。 16Q…...

自我介绍思考
1.引导面试官有重点的看你简历 2.在引导部分暗示他我是最适合这个岗位的 面试官在考察什么? a.你的表述是否一致b.考察你的语言表达能力,逻辑思维能力,总结概括能力c.考察你对现场的把控能力d.对时间的把控能力 怎么做? 1.写逐…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

