LeetCode算法位运算—只出现一次的数字
目录
136. 只出现一次的数字 - 力扣(LeetCode)
解题思路:
代码:
运行结果:
补充
异或的重要性质
136. 只出现一次的数字 - 力扣(LeetCode)
给你一个 非空 整数数组
nums,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1] 输出:1示例 2 :
输入:nums = [4,1,2,1,2] 输出:4示例 3 :
输入:nums = [1] 输出:1提示:
1 <= nums.length <= 3 * 104-3 * 104 <= nums[i] <= 3 * 104- 除了某个元素只出现一次以外,其余每个元素均出现两次。
解题思路:异或运算(^)的性质:
- 异或运算满足交换律和结合律,即a^b^c = a^(b^c)。
- 对于任何数x,x^x=0,即一个数与自己异或的结果为0。
- 对于任何数x,x^0=x,即一个数与0异或的结果为它本身。
考虑到这些性质,让我们看一下代码的执行过程:
- 初始化变量a为0。
- 遍历数组nums中的每个元素:
- 将a与当前元素进行异或操作,即a^=nums[i]。
- 异或操作会将出现两次的数字消除,因为两个相同的数字异或的结果为0。
- 异或操作会将只出现一次的数字留下,因为任何数字与0异或的结果为它本身。
- 最终,a将保留只出现一次的数字。
- 返回变量a作为结果。
现在,让我们通过一个案例来解析这段代码:
假设输入数组nums为[2, 4, 2, 1, 4],其中只有数字1只出现一次,其他数字都出现了两次。
执行过程如下:
- 初始化变量a为0。
- 遍历数组nums:
- 第一次循环:a^=2,a的值变为2。
- 第二次循环:a^=4,a的值变为6。
- 第三次循环:a^=2,a的值变为4。
- 第四次循环:a^=1,a的值变为5。
- 第五次循环:a^=4,a的值变为1。
- 返回a的值1作为结果。
代码:class Solution {public int singleNumber(int[] nums) {int a=0;for(int i=0;i<nums.length;i++){a^=nums[i];}return a;} }
运行结果:
补充
异或的重要性质
结合律:异或运算满足结合律,即对于任意三个数a、b和c,满足 (a ^ b) ^ c = a ^ (b ^ c)。
自反性:任何数与自身进行异或运算的结果为0,即 a ^ a = 0。这是因为异或运算可以看作是"无进位相加",而相同的位进行异或运算结果为0。
零元素:0是异或运算的零元素,即对于任何数a,满足 a ^ 0 = a。这是因为异或运算中,任何数与0进行异或运算结果为它本身。
逆元素:每个数在异或运算中都有逆元素,即对于任何数a,存在一个数b,满足 a ^ b = 0。这意味着可以通过异或运算来撤销一个数的影响。
消除相同元素:当数组中有成对出现的相同元素时,对整个数组进行异或运算,最终结果为0。这是因为相同元素异或的结果为0,而异或运算满足交换律和结合律。
这些性质使得异或运算在很多场景下非常有用,例如查找只出现一次的数字、判断两个数是否相等、交换两个变量的值等。通过利用这些性质,可以简化问题的处理和求解。
相关文章:
LeetCode算法位运算—只出现一次的数字
目录 136. 只出现一次的数字 - 力扣(LeetCode) 解题思路: 代码: 运行结果: 补充 异或的重要性质 136. 只出现一次的数字 - 力扣(LeetCode) 给你一个 非空 整数数组 nums ,除了某…...
vcpkg manifest 的使用
最近项目上要使用 CMakeLists 管理,由于 Windows 版本有依赖到 vcpkg 提供的库,所以需要使用 vcpkg manifest 来统一设置库的版本,方便后续维护 推荐一个文章,介绍的可以说是非常全面了 VCPKG 特性 - Versioning 不过里面也有一些…...

选择什么电容笔比较好?平板手写笔推荐
由于苹果Pencil的热销,让华国内市场上,也出现了不少的平替式电容笔,这些产品,有好有坏,价格也很公道。不过,也有很多产品的价格都很平价。我是一个拥有多年经验的数码发烧友,在前几年就开始用上…...
pdf转二维码怎么做?pdf二维码制作简单技巧
pdf是一种很常见的文件储存格式,一般通知、发票、简历都会保存为这种格式来使用,那么需要将pdf格式文件做成二维码,该用什么方式来制作呢?下面给大家分享一个pdf转二维码的在线工具,可以通过上传文件一键生成二维码&am…...

【CANoe】TX Self-ACK自应答配置与CPAL实现
一、引言 在测试CAN&CANFD通信或者网络管理的时候,我们经常遇到使用报文(网络管理报文或者通信报文)唤醒被测件这个测试点,如果测试比较多的情况下,我们就会发现,如果CANoe没有接被测件或者被测件没有…...
MATLAB mat矩阵和Python npy矩阵转换)
(Python)MATLAB mat矩阵和Python npy矩阵转换
Python np.ndarray矩阵转换为MATLAB mat文件 import numpy as npimport scipy.io as iomat_path mat_save_pathmat np.zeros([6, 128])io.savemat(mat_path, {name: mat})Python读取MATLAB mat文件 import numpy as np from scipy import iomat io.loadmat(your_mat_file.…...
)
Flink1.14 SourceReader概念入门讲解与源码解析 (三)
目录 SourceReader 概念 SourceReader 源码方法 void start(); InputStatus pollNext(ReaderOutput output) throws Exception; List snapshotState(long checkpointId); CompletableFuture isAvailable(); void addSplits(List splits); 参考 SourceReader 概念 Sour…...
PS运行中缺失d3dcompiler_47.dll问题的5个有效修复方法总结
在使用ps作图的时候,我们有时会遇到一些问题,其中之一就是“PS运行中缺失d3dcompiler_47.dll”的问题。这个问题可能会导致PS无法正常运行,“d3dcompiler_47.dll”。这是一个动态链接库文件,它是DirectX的一部分,主要负…...
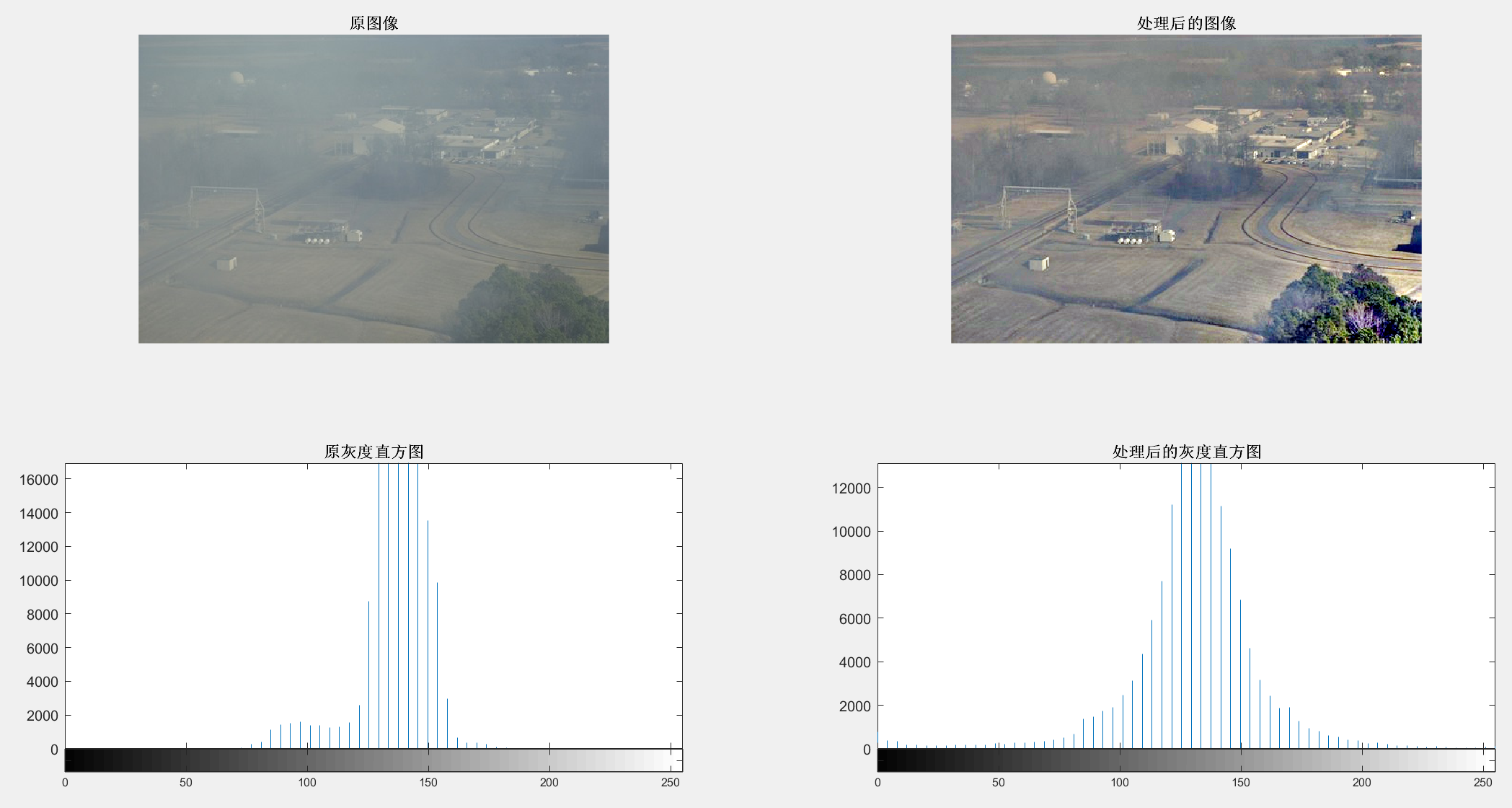
【MATLAB-Retinex图像增强算法的去雾技术】
续:【MATLAB-基于直方图优化的图像去雾技术】 【MATLAB-Retinex图像增强算法的去雾技术】 1 原图2 MATLAB实现代码3 结果图示 参考书籍:计算机视觉与深度学习实战:以MATLAB、Python为工具, 主编:刘衍琦, 詹福宇, 王德建…...

使用 2 个 HSplitView 在 swiftUI 中创建一个 3 窗格界面
Pet*_*ter 8 嗯,我会的。在断断续续地挣扎了几个星期之后,在我问这个问题一个小时后,我似乎解决了它!只需将第二个 HSplitView 的 layoutPriority 设置为 1,并将中心视图也设置为 1。当你想到它时是有道理的࿱…...

【C++ 操作符重载:定制自己的运算符行为】
在C编程中,操作符重载是一项强大的特性,它允许程序员定制内置运算符的行为,使它们适用于用户自定义的数据类型。这篇博客将介绍什么是操作符重载,如何使用它,以及一些最佳实践。 什么是操作符重载? 操作符…...

Android Fragment 基本概念和基本使用
Android Fragment 基本概念和基本使用 一、基本概念 Fragment,简称碎片,是Android 3.0(API 11)提出的,为了兼容低版本,support-v4库中也开发了一套Fragment API,最低兼容Android 1.6。 过去s…...

xml schema中的all元素
说明 xml schema中的all元素表示其中的子元素可以按照任何顺序出现,每个元素可以出现0次或者1次。 https://www.w3.org/TR/xmlschema-1/#element-all maxOccurs的默认值是1,minOccurs 的默认值是1。 举例 <element name"TradePriceRequest&…...

Java8实战-总结42
Java8实战-总结42 用Optional取代null应用 Optional 的几种模式默认行为及解引用 Optional 对象两个 Optional 对象的组合使用 filter 剔除特定的值 用Optional取代null 应用 Optional 的几种模式 默认行为及解引用 Optional 对象 采用orElse方法读取这个变量的值࿰…...

实现日期间的运算——C++
😶🌫️Take your time ! 😶🌫️ 💥个人主页:🔥🔥🔥大魔王🔥🔥🔥 💥代码仓库:🔥🔥魔…...
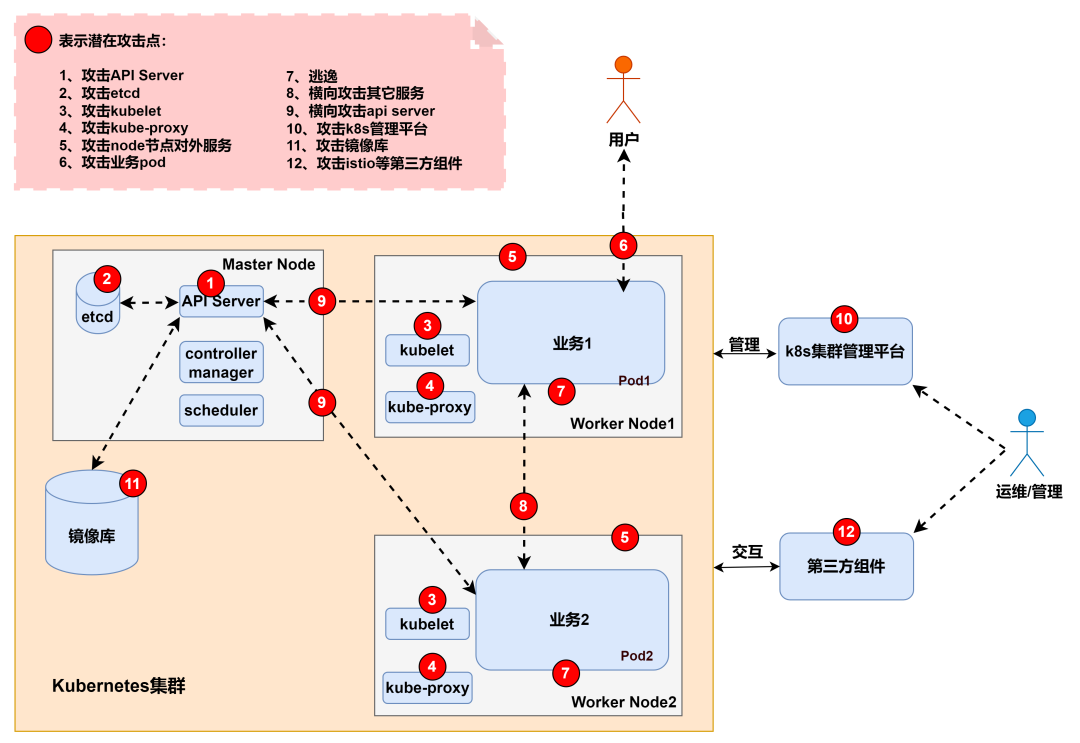
云上攻防-云原生篇K8s安全Config泄漏Etcd存储Dashboard鉴权Proxy暴露
文章目录 云原生-K8s安全-etcd未授权访问云原生-K8s安全-Dashboard未授权访问云原生-K8s安全-Configfile鉴权文件泄漏云原生-K8s安全-Kubectl Proxy不安全配置 云原生-K8s安全-etcd未授权访问 攻击2379端口:默认通过证书认证,主要存放节点的数据&#x…...

ChatGPT 的工作原理学习 难以理解 需要先找个容易的课来跟下。
ChatGPT 的工作原理 传统搜超搜引擎原理:蜘蛛抓取和数据收集,用户交互查找。 ChatGPT 的工作原理:数据收集称为预训练,用户响应阶段称为推理。 ChatGPT是一种基于自然语言处理技术的人工智能模型,它的工作原理建立在…...
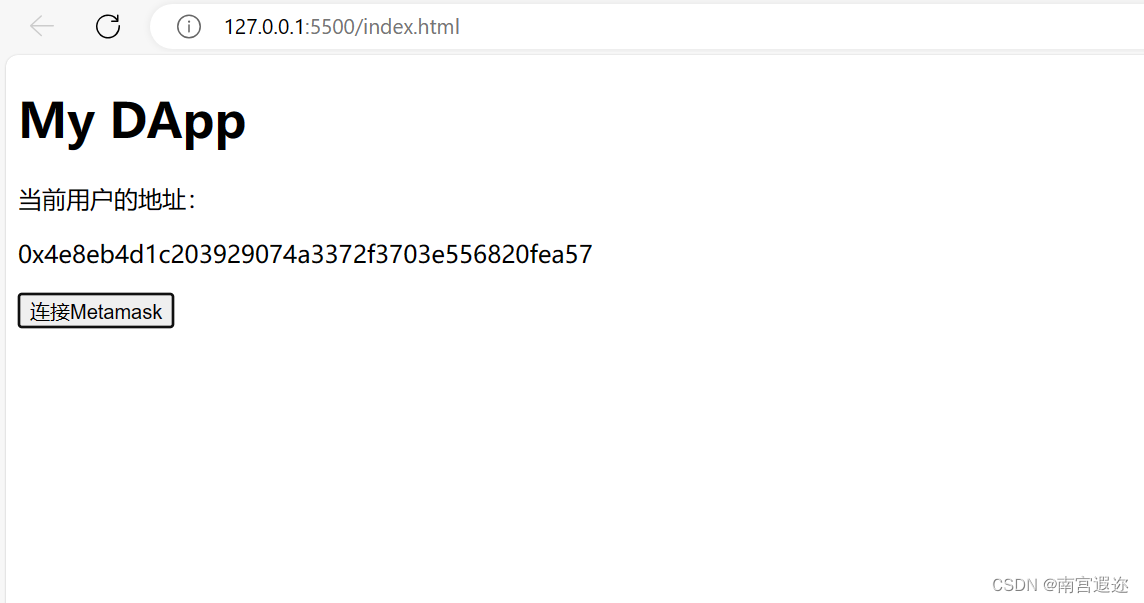
5.DApp-前端网页怎么连接MetaMask
题记 在前端网页连接metamask,以下是全部操作流程和代码。 编写index.html文件 index.html文件如下: <!DOCTYPE html> <html> <head> <title>My DApp</title> <!--导入用于检测Metamask提供者的JavaScript库--> &l…...
手机应用app打开游戏显示连接服务器失败是什么原因?排查解决方案?
亲爱的同学们,有时候我们在使用手机设备时,可能会遇到一个很头疼的问题——连接服务器失败。这个问题不仅让我们感到困扰,还影响到了我们的用户体验。那么,我们究竟能如何解决这个问题呢?今天,笔者就和大家…...

【Java学习之道】指引篇:从入门到入世
引言 你是否曾为找不到适合自己的Java学习之路而烦恼?是否想摆脱混乱的Java知识体系,找到一条从入门到精通的捷径?来《Java学习之道》吧,本专栏为你量身打造,让我们一起轻松踏上Java学习之旅! 第一章、Jav…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...

C++ Saucer 编写Windows桌面应用
文章目录 一、背景二、Saucer 简介核心特性典型应用场景 三、生成自己的项目四、以Win32项目方式构建Win32项目禁用最大化按钮 五、总结 一、背景 使用Saucer框架,开发Windows桌面应用,把一个html页面作为GUI设计放到Saucer里,隐藏掉运行时弹…...
