主定理(简化版)
主定理(Master Theorem)是用于分析递归算法时间复杂度的一个重要工具。它适用于形式化定义的一类递归关系,通常采用分治策略解决问题的情况。
假设我们有一个递归算法,它将问题分解成 a a a 个子问题,每个子问题的规模是原问题的 1 b \frac{1}{b} b1,解决每个子问题的代价是 f ( n ) f(n) f(n),而将子问题的解合并成原问题的解的代价是 g ( n ) g(n) g(n)。那么该递归算法的时间复杂度可以表示为:
T ( n ) = a ⋅ T ( n b ) + f ( n ) T(n)=a·T(\frac{n}{b})+f(n) T(n)=a⋅T(bn)+f(n)
其中, a ≥ 1 , b > 1 a ≥ 1,b > 1 a≥1,b>1 是常数, f ( n ) f(n) f(n) 是解决一个规模为 n n n 的问题所需的工作量, g ( n ) g(n) g(n) 是合并子问题的解的工作量。
主定理的三种情况:
- I F IF IF f ( n ) = O ( n l o g b ( a − ε ) ) f(n) = O(n^ {log_b(a - ε)}) f(n)=O(nlogb(a−ε)),and ε > 0 ε > 0 ε>0,Then T ( n ) = Θ ( n l o g b ( a ) ) T(n) = Θ(n^{log_b(a)}) T(n)=Θ(nlogb(a))
- I F IF IF f ( n ) = Θ ( n l o g b ( a ) ⋅ l o g k n ) f(n) = Θ(n^{log_b(a)} ·log^k n) f(n)=Θ(nlogb(a)⋅logkn),and k ≥ 0 k ≥ 0 k≥0,Then T ( n ) = Θ ( n l o g b ( a ) ⋅ l o g k + 1 n ) T(n) = Θ(n^{log_b(a)} · log^{k+1} n) T(n)=Θ(nlogb(a)⋅logk+1n)
- I F IF IF f ( n ) = Ω ( n l o g b ( a + ε ) ) f(n) = Ω(n^{log_b(a + ε)}) f(n)=Ω(nlogb(a+ε)),and ε > 0 ε > 0 ε>0, a ⋅ f ( n b ) ≤ c ⋅ f ( n ) a · f(\frac{n}{b}) ≤ c · f(n) a⋅f(bn)≤c⋅f(n) 对于某个常数 c < 1 c < 1 c<1 和所有足够大的 n n n 成立,Then T ( n ) = Θ ( f ( n ) ) T(n) = Θ(f(n)) T(n)=Θ(f(n))
情况一:
T ( n ) = 4 T ( n 2 ) + n T(n)=4T(\frac{n}{2})+n T(n)=4T(2n)+n
其中 a = 4 ≥ 1 , b = 2 > 1 , f ( n ) = n , l o g 2 4 = 2 > 1 a = 4\ge1,b = 2>1,f(n) = n,log_{2}4=2>1 a=4≥1,b=2>1,f(n)=n,log24=2>1。
根据主定理的第一种情况: f ( n ) = O ( n l o g b ( a − ε ) ) f(n) = O(n^ {log_b(a - ε)}) f(n)=O(nlogb(a−ε))
可得 n = O ( n l o g 2 4 − ε ) = O ( n 2 ) n=O(n^{log_{2}4−ε})=O(n^{2}) n=O(nlog24−ε)=O(n2)
∴ T ( n ) = Θ ( n 2 ) \therefore T(n)=Θ(n^{2}) ∴T(n)=Θ(n2)
情况二:
T ( n ) = 4 T ( n 2 ) + n 2 T(n)=4T(\frac{n}{2})+n^{2} T(n)=4T(2n)+n2
其中 a = 4 ≥ 1 , b = 2 > 1 , f ( n ) = n 2 , l o g 2 4 = 2 a = 4\ge1,b = 2>1,f(n) = n^{2},log_{2}4=2 a=4≥1,b=2>1,f(n)=n2,log24=2。
根据主定理的第二种情况: f ( n ) = O ( n l o g b ( a ) l o g k n ) f(n) = O(n^ {log_b(a )}log^{k}n) f(n)=O(nlogb(a)logkn)
可得 n 2 = Θ ( n l o g 2 4 l o g 0 n ) = Θ ( n 2 ) n^{2}=Θ(n^{log_{2}4}log^{0}n)=Θ(n^{2}) n2=Θ(nlog24log0n)=Θ(n2)
∴ T ( n ) = Θ ( n 2 l o g n ) \therefore T(n)=Θ(n^{2}logn) ∴T(n)=Θ(n2logn)
情况三:
T ( n ) = 2 T ( n 2 ) + n 2 T(n)=2T(\frac{n}{2})+n^{2} T(n)=2T(2n)+n2
其中 a = 2 ≥ 1 , b = 2 > 1 , f ( n ) = n 2 , l o g 2 2 = 1 < 2 a = 2\ge1,b = 2>1,f(n) = n^{2},log_{2}2=1<2 a=2≥1,b=2>1,f(n)=n2,log22=1<2。
根据主定理的第三种情况: f ( n ) = Ω ( n l o g b ( a ) + ε ) f(n) = Ω(n^ {log_b(a )+ε }) f(n)=Ω(nlogb(a)+ε)
可得 n 2 = Ω ( n l o g 2 2 + ε ) = Ω ( n 1 + ε ) n^{2}=Ω(n^{log_{2}2+ε})=Ω(n^{1+ε}) n2=Ω(nlog22+ε)=Ω(n1+ε)
但我们还需要检查是否满足 a ⋅ f ( n b ) ≤ c ⋅ f ( n ) a · f(\frac{n}{b}) ≤ c · f(n) a⋅f(bn)≤c⋅f(n) 的条件:
2 ⋅ ( n / 2 ) 2 ≤ c ⋅ n 2 n 2 / 2 ≤ c ⋅ n 2 1 / 2 ≤ c 2·(n/2)^{2}≤c·n^{2}\\ n^{2}/{2}≤c·n^{2}\\ 1/2≤c 2⋅(n/2)2≤c⋅n2n2/2≤c⋅n21/2≤c
对于任何小于 1/2 的常数 c c c,上述不等式都成立
∴ T ( n ) = Θ ( n 2 ) \therefore T(n)=Θ(n^{2}) ∴T(n)=Θ(n2)
相关文章:
)
主定理(简化版)
主定理(Master Theorem)是用于分析递归算法时间复杂度的一个重要工具。它适用于形式化定义的一类递归关系,通常采用分治策略解决问题的情况。 假设我们有一个递归算法,它将问题分解成 a a a 个子问题,每个子问题的规模…...

HTTP1.0和HTTP2.0的区别
相同点:所有的HTTP请求都要基于TCP连接。 HTTP1.0:每次发送请求时建立一个TCP连接,得到响应后,释放TCP连接。 HTP1.1:**相比于1.0,引入了Keep live,客户端得到响应后,不会立刻释放T…...
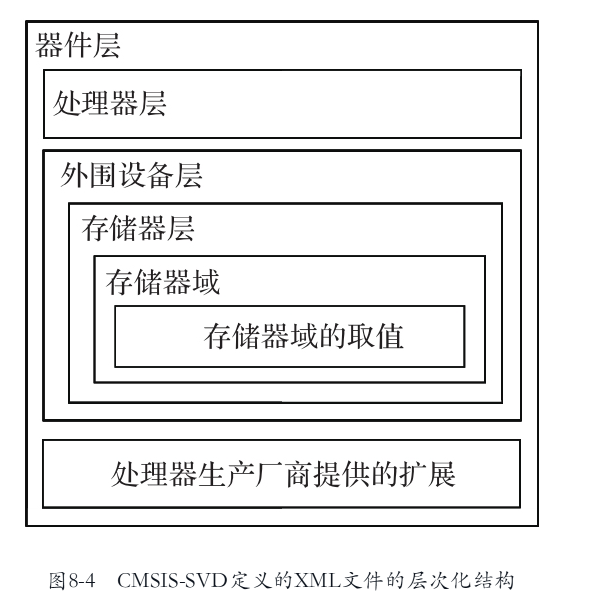
ARM资源记录《AI嵌入式系统:算法优化与实现》第八章(暂时用不到)
1.CMSIS的代码 书里给的5,https://github.com/ARM-software/CMSIS_5 现在有6了,https://github.com/ARM-software/CMSIS_6 这是官网的书,介绍cmsis函数的https://arm-software.github.io/CMSIS_5/Core/html/index.html 2.CMSIS介绍 Cort…...

微信小程序2
一,视图层 1.什么视图层 框架的视图层由 WXML 与 WXSS 编写,由组件来进行展示。 将逻辑层的数据反映成视图,同时将视图层的事件发送给逻辑层。 WXML(WeiXin Markup language) 用于描述页面的结构。 WXS(WeiXin Script) 是小程序的一套脚本语…...
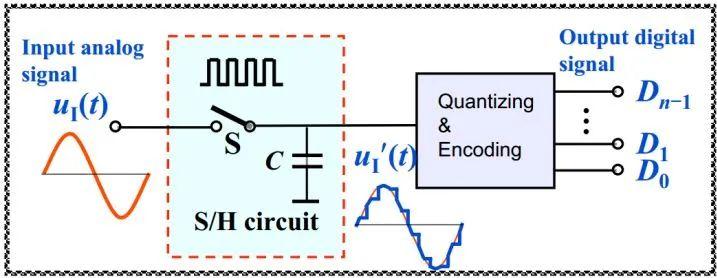
G.711语音编解码器详解
语音编解码利用人听觉上的冗余对语音信息进行压缩从而达到节省带宽的目的。值得注意的是,本文说的是语音编解码器,也就Speech codec,而常用的还有另一种编解码器称作音频编解码器,英文是Audio codec,它们的区别如下。 以前在学校的时候研究了很多VoIP的编解码器从G.723到A…...

蓝桥杯每日一题2023.10.17
迷宫 - 蓝桥云课 (lanqiao.cn) 题目描述 样例: 01010101001011001001010110010110100100001000101010 00001000100000101010010000100000001001100110100101 01111011010010001000001101001011100011000000010000 0100000000101010001101000010100000101010101100…...
16.SpringBoot前后端分离项目之简要配置一
SpringBoot前后端分离项目之简要配置一 前面对后端所需操作及前端页面进行了了解及操作,这一节开始前后端分离之简要配置 为什么要前后端分离 为了更低成本、更高效率的开发模式。 前端有一个独立的服务器。 后端有一个独立的服务器。两个服务器之间实时数据交换…...

Probability Calibration概率校准大比拼:性能、应用场景和可视化对比总结
在机器学习中,概率校准(Probability Calibration)是一个重要的概念。简单来说,概率校准就是将分类器输出的原始预测概率转换为更准确、更可靠的概率值。这样做的目的是为了让模型的预测结果更接近实际情况,从而提高模型在特定应用场景中的可用性。 在Python的Scikit-Lear…...
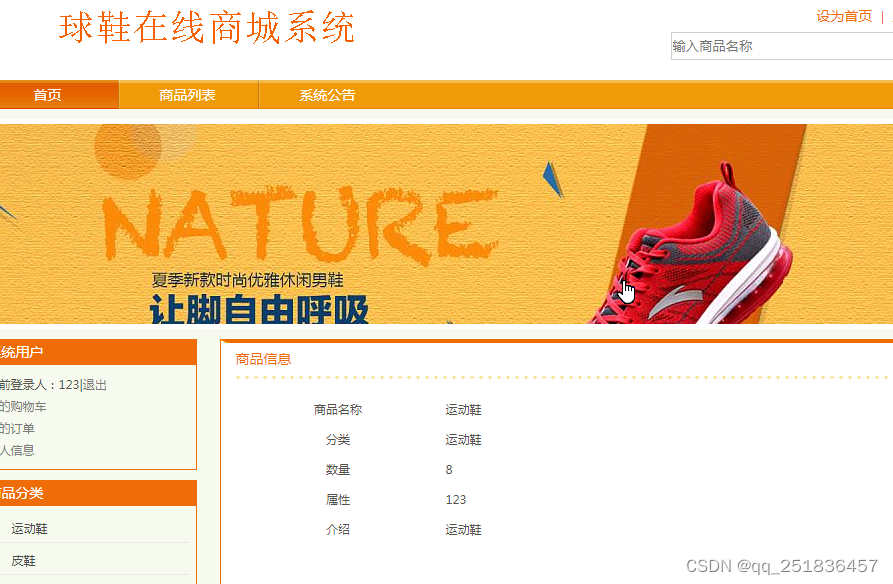
PHP 球鞋在线商城系统mysql数据库web结构apache计算机软件工程网页wamp计算机毕业设计
一、源码特点 PHP球鞋在线商城系统是一套完善的web设计系统,对理解php编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 php球鞋在线商城系统 代码 https://download.csdn.net/download/qq_41221322/8843725…...
使用Apache和内网穿透实现私有服务公网远程访问——“cpolar内网穿透”
文章目录 前言1.Apache服务安装配置1.1 进入官网下载安装包1.2 Apache服务配置 2.安装cpolar内网穿透2.1 注册cpolar账号2.2 下载cpolar客户端 3. 获取远程桌面公网地址3.1 登录cpolar web ui管理界面3.2 创建公网地址 4. 固定公网地址 前言 Apache作为全球使用较高的Web服务器…...
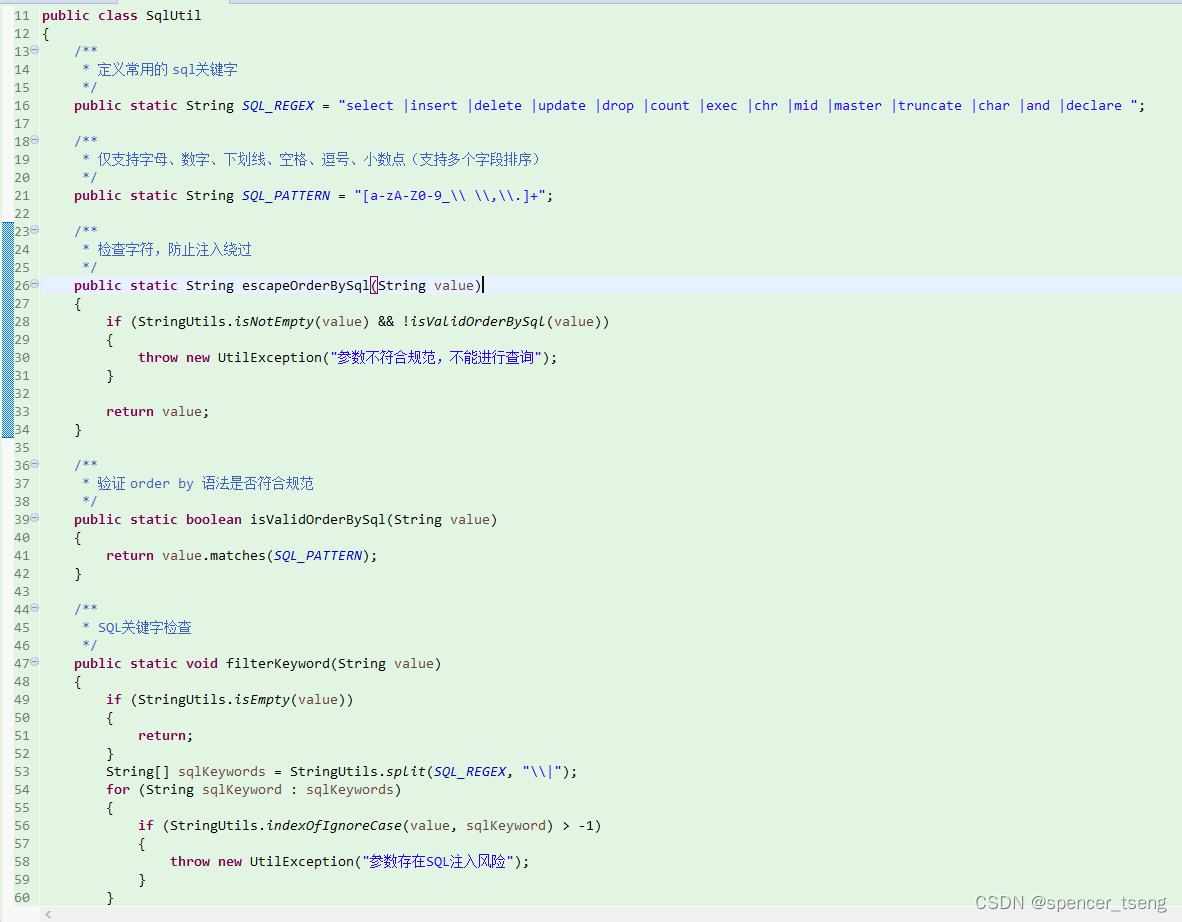
PreparedStatement
使用参数化查询:使用预编译的语句和参数化查询来执行SQL语句,而不是将用户输入直接嵌入到SQL语句中。这将帮助防止恶意输入注入SQL语句。...

CSS3 新增属性-边框圆角-文字阴影-盒子阴影
边框圆角 CSS 边框圆角可以通过 border-radius 属性来实现。该属性用于设置元素的圆角大小,支持四个值分别表示上左、上右、下右和下左四个角的圆角半径大小,也可以使用两个值分别表示上下和左右两个方向的圆角大小,甚至可以只使用一个值来…...

制作.a静态库 (封盒)
//云库房间 1.GitHub上创建开源框架项目须包含文件: LICENSE:开源许可证;README.md:仓库说明文件;开源项目;(登录GitHub官网) 2. 云仓储库构建成功(此时云库中没有内容三方框架)!!! 3. 4.5. //…...

一台服务器,一个新世界
我如何看待服务器 当我拥有一台服务器,我看到的不仅仅是一块硬件,而是一扇打开未来的大门,一个我可以将自己的愿景和创意投射到其中的平台。这台服务器是我的工具,我的画布,我将在其中铸造我的数字梦想。 第一步我要…...

keep-alive 是 Vue 的一个内置组件,用于缓存其他组件的实例,以避免重复渲染和销毁,它可以在需要频繁切换的组件之间提供性能优化
目录 keep-alive 使用 keep-alive 的示例代码: 手动清除组件缓存的示例代码: keep-alive 组件有以下几个优点: keep-alive 的原理: 使用 keep-alive 组件,你可以包裹需要缓存的组件,然后这些组件在切…...
Python类和对象)
(八)Python类和对象
Python 语言在设计之初,就定位为一门面向对象的编程语言,“Python 中一切皆对象”就是对 Python 这门编程语言的完美诠释。 类和对象是 Python 的重要特征,相比其它面向对象语言,Python 很容易就可以创建出一个类和对象。同时&am…...

黑客利用人工智能窃取医疗数据的 7 种方式
人工智能被描述为医疗保健行业的一把双刃剑。基于人工智能的系统可以分析大量数据并在早期和可治疗的阶段检测疾病,它们可以比任何人类更快地诊断症状,并且人工智能正在帮助药物开发,使新的救命药物得以识别并将其推向市场速度更快且成本显着…...

OJ第四篇
文章目录 链表分割环形链表有效的括号 链表分割 链接: 链表分割 虽然这个题牛客网中只有C,但是无所谓,我们只要知道C是兼容C的就可以了 至于说这个题的思路,我们就弄两个链表,把小于x的结点放到一个链表中,剩下的放到另一个链表…...

L2-022 重排链表
给定一个单链表 L1→L2→⋯→Ln−1→Ln,请编写程序将链表重新排列为 Ln→L1→Ln−1→L2→⋯。例如:给定L为1→2→3→4→5→6,则输出应该为6→1→5→2→4→3。 输入格式: 每个输入包含1个测试用例。每个测试用例…...

css 特别样式记录
一、 这段代码神奇的地方在于, 本来容器的宽度只有1200px,如果不给img赋予宽度100%,那么图片 会超出盒子,如果给了img赋予了宽度100%,多个图片会根据自己图片大小的比例,去分完那1200px,如图二。…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...
