Python 机器学习入门之逻辑回归
系列文章目录
第一章 Python 机器学习入门之线性回归
第一章 Python 机器学习入门之梯度下降法
第一章 Python 机器学习入门之牛顿法
第二章 Python 机器学习入门之逻辑回归
逻辑回归
- 系列文章目录
- 前言
- 一、逻辑回归简介
- 二、逻辑回归推导
- 1、问题
- 2、Sigmoid函数
- 3、目标函数
- 3.1 让步比
- 3.2 极大似然估计
- 3.3 推导
- 4、代价函数
- 5、最大化似然函数
- 三、逻辑回归实现
- 结果展示
前言
第二次实验开始了,内容是逻辑回归,听起来像是线性回归的兄弟,然而仔细查阅后发现逻辑回归其实是一种分类算法;
我们知道回归算法的结果建立在连续的数据上,分类算法的结果建立在离散的数据上;因此逻辑回归本质上是一种分类算法,那问题就来了,一个分类算法为啥叫回归呢?

一、逻辑回归简介
百科定义:
logistic回归又称logistic回归分析,是一种广义的线性回归分析模型,常用于数据挖掘,疾病自动诊断,经济预测等领域。
简单来说,逻辑回归还是建立在我们之前学习的线性回归模型基础上,使用回归的方法来实现分类的目的;就好像同在一个专业学习,有些人学习计算机是为了成为一个优秀的程序员,有些人学计算机是为了挑选出优秀的程序员,结果不一样但在过程中是有很多的相似之处的。
二、逻辑回归推导
1、问题
假设你是一个大学系的管理员,你想根据两个考试的结果确定每个申请人的录取机会。您可以将以前申请者的历史数据用作逻辑回归的培训集。对于每个培训示例,您都有申请人的两次考试成绩和录取决定。为了实现这一点,我们将建立一个分类模型,根据考试成绩估计入学概率。(取自吴恩达机器学习中文版课后题)
先来分析一下,如果我们现在使用线性回归模型来分析该该题,我们最后得出的结论应该是根据考试成绩来预测入学成绩,但是现在结果需要我们来判断是否能成功入学,那我们就在此基础上对之前的入学成绩设定阈值,根据该阈值对结果进行分类来选择是否录取;
但是线性回归模型往往是一条斜线,如何满足结果不是0就是1呢?因此我们引入了Sigmoid函数。
2、Sigmoid函数
先看一下线性回归模型假设函数
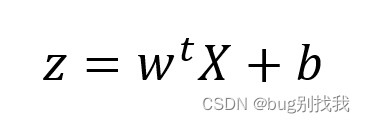
sigmoid函数公式如下
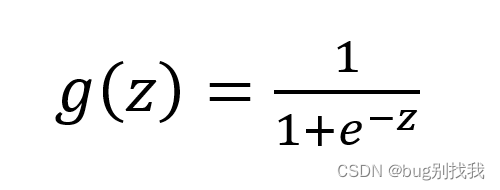
将线性回归模型的预测值视为上式的自变量z,可得出下图结果
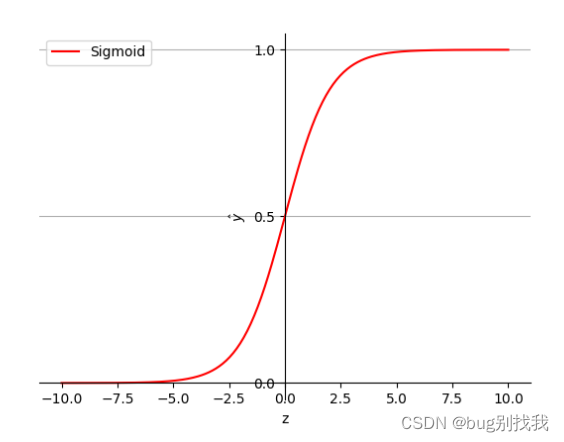
然而上图结果仍然不是我们真正需要的结果,我们需要的是一个二元离散模型,结果非1即0,因此我们还需处理一下,根据与阈值的差值判断结果
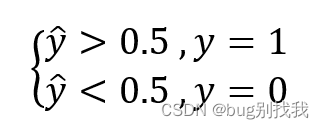
当y ̂ ==0.5时,我们根据实际情况来定;同时上面的阈值是我们手动设置的(并不一定需要0.5),依情况而定,这也是逻辑回归模型的优势之一
3、目标函数
在上面的sigmiod函数上我们建立了逻辑回归的假设函数,我们想要得到它的目标函数,首先得知道自变量X和结果变量y之间的关系,因此我们引入两个概念让步比和极大似然估计
3.1 让步比
让步比可以理解成有利于某一特定事件的概率,如下

3.2 极大似然估计
思想:如果一个事件发生了,那么发生这个事件的概率就是最大的;对于样本i,其类别为
y ̂ ∈(0,1),对于样本i,可以把h(Xi)看成是一种概率;yi对应是1时,概率是h(Xi)(即Xi属于1的概率,即p(Y=1|X));yi对应是0时,概率是1-h(Xi)(Xi属于0的概率,即p(Y=0|X)
已知下式
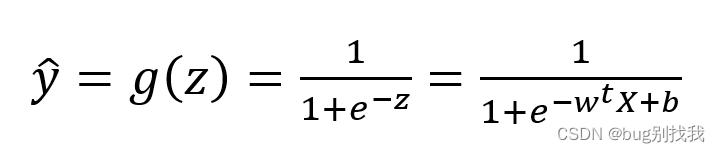
在这里使用极大似然估计做一个假设,假设y ̂ 为样本x为正例的概率,那么1-y ̂ 为样本x为负例的概率
在此基础上我们可以将让步比的对数形式转成特征值相关式子;
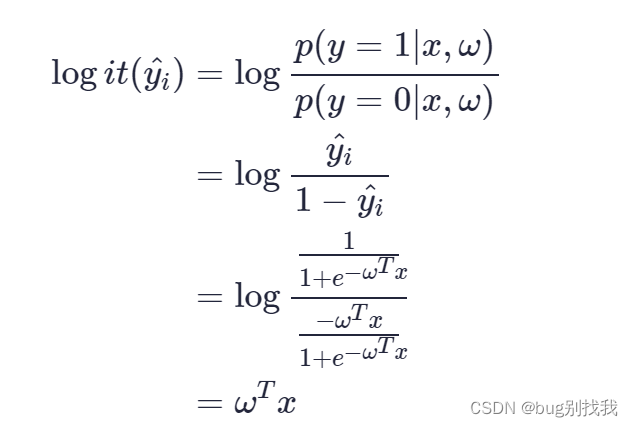
然而我们更想要的是预测值和它发生的概率之间的关系,即让步比之间的逆形式
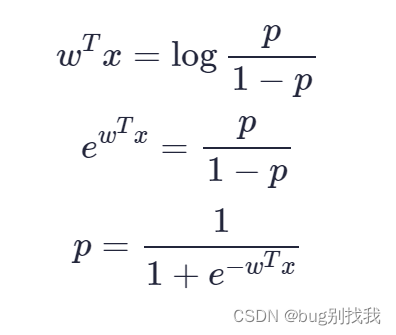
3.3 推导
已知样本X结果分类的概率
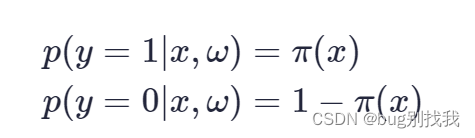
将上式联系得y的概念分布函数
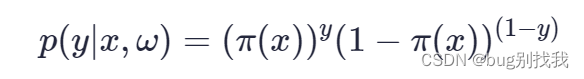
通过y的概率分布函数表达式即可得似然函数为(m为样本数量)
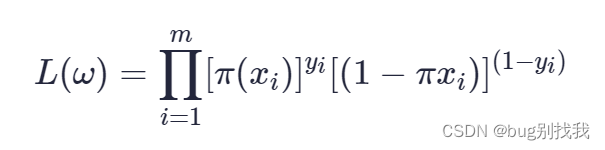
通过似然函数得到对数似然函数即目标函数
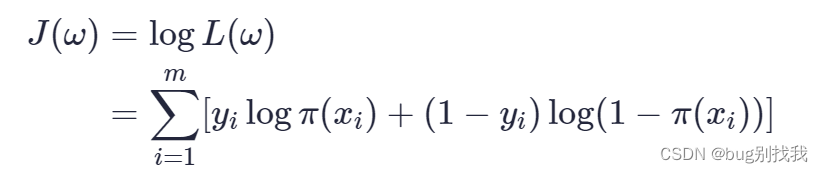
4、代价函数
对于二分类问题,分别考虑y=1和y=0的情况
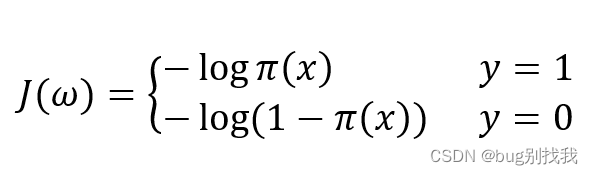
5、最大化似然函数
最大似然估计是似然函数最初也是最自然的应用,似然函数取得最大值表示相应的参数能够使得统计模型最为合理;
可以使用梯度上升法和牛顿法两种优化方法,这里说一下梯度上升法,本质和之前的梯度下降原理一一样,展开一阶梯度来求最优解;先求目标函数对参数w的偏导
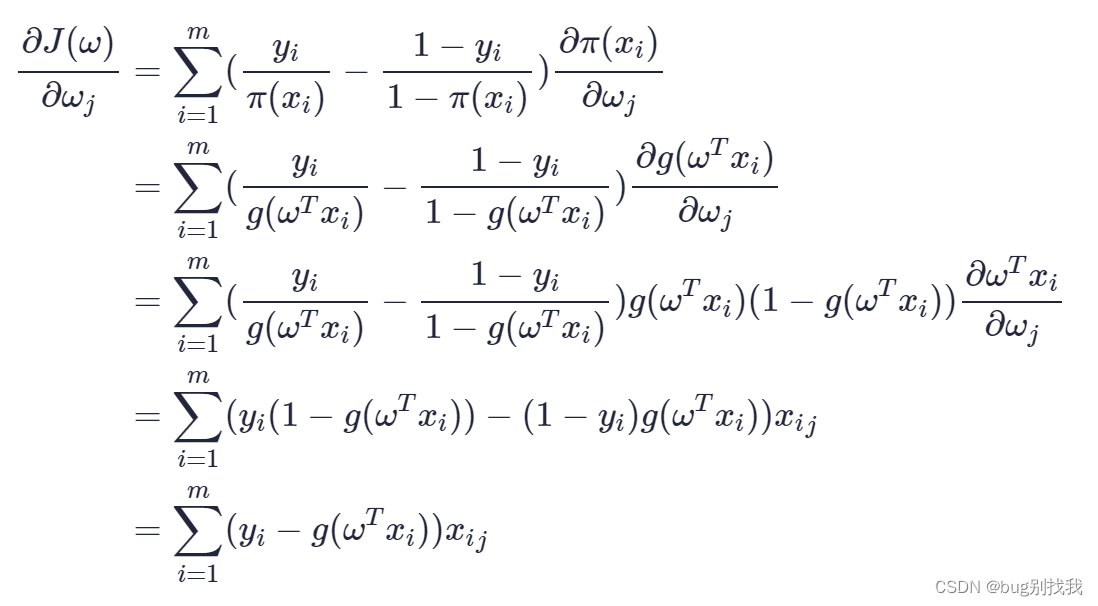
因此逻辑回归模型的梯度下降函数如下,wj代表第j个模型参数
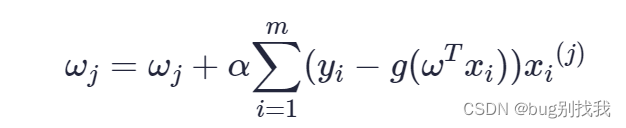
三、逻辑回归实现
结果展示
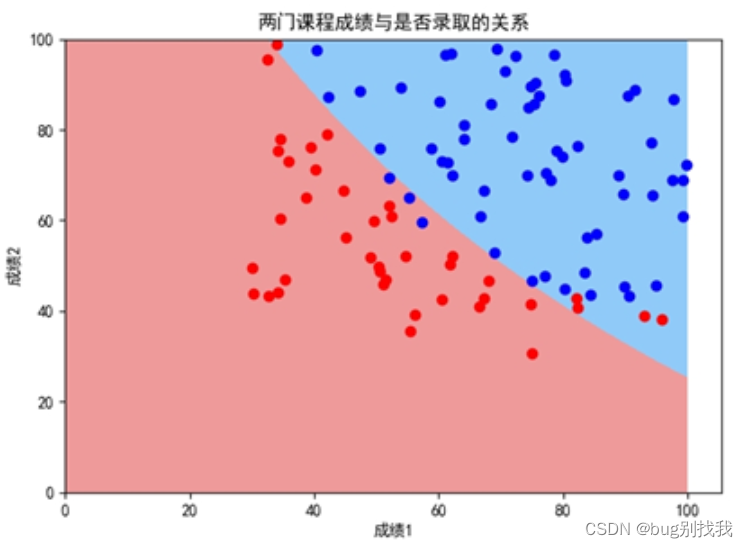
相关文章:

Python 机器学习入门之逻辑回归
系列文章目录 第一章 Python 机器学习入门之线性回归 第一章 Python 机器学习入门之梯度下降法 第一章 Python 机器学习入门之牛顿法 第二章 Python 机器学习入门之逻辑回归 逻辑回归 系列文章目录前言一、逻辑回归简介二、逻辑回归推导1、问题2、Sigmoid函数3、目标函数3.1 让…...

现货白银赚钱有风险吗?
跟现货黄金一样,现货白银市场是一个公平公正的市场,即使是中小投资者,也能拥有平等的获利机会,同样可以借助平台所给予的资金杠杆,实现个人财富的快速增值。 很多人都是冲着现货白银的财富效应而进入这个市场ÿ…...

Debian衍生桌面项目SpiralLinux12.231001发布
SpiralLinux 是一个从 Debian 衍生出来的桌面项目,其重点是在所有主要桌面环境中实现简洁性和开箱即用的可用性。 spiral Linux 是为刚接触 Linux 世界的人们量身定制的发行版。这是 GeckoLinux 开发人员的创意,他更喜欢保持匿名。尽管他不愿透露姓名&a…...

元宇宙在技术大爆炸时代迎来链游新世界
元宇宙是一个完全虚拟的世界,人们可以在其中互动,就像在现实世界中一样。 随着元宇宙概念不断的被深化,目前许多用户群体已经注意到并加入元宇宙领域。而元宇宙比较火的场景有社交、游戏、虚拟会议等,在许多方面,游戏一…...

9中间件-Redis、MQ---进阶
mq进阶 RabbitMQ 怎么避免消息丢失? 把消息持久化磁盘,保证服务器重启消息不丢失。 每个集群中至少有一个物理磁盘,保证消息落入磁盘。#RabbitMQ 的消息是怎么发送的? 首先客户端必须连接到 RabbitMQ 服务器才能发布和消费消息&…...

JVM(Java Virtual Machine)内存模型篇
前言 本文是JVM系列的内存模型篇,参考资料为《深入理解Java虚拟机》,本文章将会以HotSpot 虚拟机为介绍基础。 1.JVM简单介绍 Java Virtual Machine是运行Java程序的基础,JVM基于C、C实现,JVM有很多种类,但是这些虚…...

对地址解析协议ARP进一步探讨
之前在讨论MAC地址和IP地址时,顺便对ARP协议做了初步的总结 (计网第三章(数据链路层)(四)(MAC地址和IP地址、ARP协议、集线器和交换机)),但是当时对ARP请求的…...

java:java.util.StringTokenizer实现字符串切割
java:java.util.StringTokenizer实现字符串切割 1 前言 java.util工具包提供了字符串切割的工具类StringTokenizer,Spring等常见框架的字符串工具类(如Spring的StringUtils),常见此类使用。 例如Spring的StringUtil…...

IPV6 ND协议--源码解析【根源分析】
ND协议介绍 ND介绍请阅读上一篇文章:IPv6知识 - ND协议【一文通透】11.NDP协议分析与实践_router solicitation报文中不携带source link-layer address-CSDN博客 ND协议定义了5种ICMPv6报文类型,如下表所示: NS/NA报文主要用于地址解析RS/…...
Python学习笔记——存储容器
食用说明:本笔记适用于有一定编程基础的伙伴们。希望有助于各位! 列表 列表类似数组,其中可以包含不同类型的元素,写法如下: list1 [Google, Runoob, 1997, 2000] list2 [1, 2, 3, 4, 5 ] list3 ["a", …...
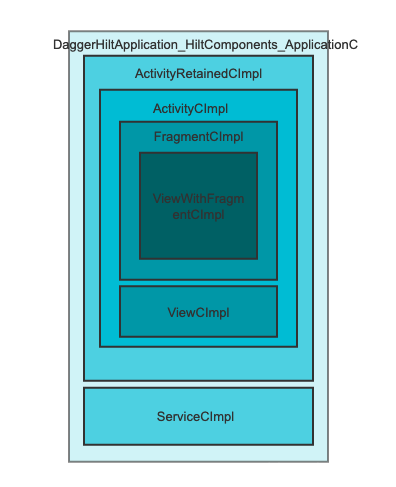
Android DI框架-Hilt
到底该如何理解<依赖注入> 模版代码:食之无味,弃之可惜 public class MainActivity extends Activity {Overrideprotected void onCreate(Bundle savedInstanceState) {super.onCreate(savedInstanceState);TextView mTextView(TextView) findVi…...

基于寄生捕食优化的BP神经网络(分类应用) - 附代码
基于寄生捕食优化的BP神经网络(分类应用) - 附代码 文章目录 基于寄生捕食优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.寄生捕食优化BP神经网络3.1 BP神经网络参数设置3.2 寄生捕食算法应用 4.测试结果…...

【Java常见的几种设计模式】
Java常见的几种设计模式 1. 单例模式(Singleton Pattern)2. 工厂模式(Factory pattern)3. 抽象工厂模式(Abstract Factory Pattern)4. 建造者模式(Builder Pattern)5. 原型模式&…...

jupyter崩溃进不去,报错module ‘mistune‘ has no attribute ‘BlockGrammar‘
是python包引起的问题 [E 2023-10-14 08:40:25.414 ServerApp] Uncaught exception GET /api/nbconvert?1697244025327 (127.0.0.1) HTTPServerRequest(protocol‘http’, host‘localhost:8090’, method‘GET’, uri‘/api/nbconvert?1697244025327’, version‘HTTP/1.1’…...
windows terminal鼠标右键打开
如果在官网上下载的是zip文件的 需要在注册表修改鼠标右键才能出来 注册表修改如下: 1.先windowsR,在命令框中输入regedit 打开注册表 2.在路径’计算机\HKEY_CLASSES_ROOT\directory\background\shell’下新建一个wt,wt下新建commond 这里…...
HTML5播放 M3U8的hls流地址
在HTML5页面上播放M3U8的hls流地址 <!DOCTYPE html> <html> <head> <meta charset"UTF-8"> <title>视频播放</title> <script src"https://cdn.jsdelivr.net/npm/hls.jslatest"></script> &…...

leetcode:101.对称二叉树
借用二叉树是否相同的代码改动左右孩子相等对应关系,即为是否对称。 /*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/bool isSameTree(struct TreeNode* p, struct Tr…...

UI自动化的适用场景,怎么做?
经常有人会问,什么样的项目才适合进行UI自动化测试呢?UI自动化测试相当于模拟手工测试,通过程序去操作页面上的控件。而在实际测试过程中,经常会遇到无法找到控件,或者因控件定义变更而带来的维护成本等问题。 哪些场…...

SpringFramewrok (1)
1、框架的概念与理解 在现实生活中,框架可以比喻为我们搭建房子的框架。 在框架的基础上,我们可以专注于我们自己的工作,而不用在意这些底层工作如何实现。 框架的优点包括以下几点: 1. 提高开发效率:框架提供了许多…...

电商独立站小程序开发方案
随着移动互联网的迅速发展,电商行业也逐渐向小程序平台转移。开发一款电商小程序对于拓展销售渠道、提高用户体验、增加用户忠诚度等方面都有着重要的意义。本文将围绕电商小程序的开发背景、需求分析、技术选型、开发流程、风险控制、商业模式和市场前景等方面进行…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
