数据结构:完全二叉树开胃菜小练习
目录
一.前言
二.完全二叉树的重要结构特点
三.完全二叉树开胃菜小练习
1.一个重要的数学结论
2.简单的小练习
一.前言
关于树及完全二叉树的基础概念(及树结点编号规则)参见:http://t.csdn.cn/imdra
http://t.csdn.cn/imdra
完全二叉树是一种非常重要的数据结构:
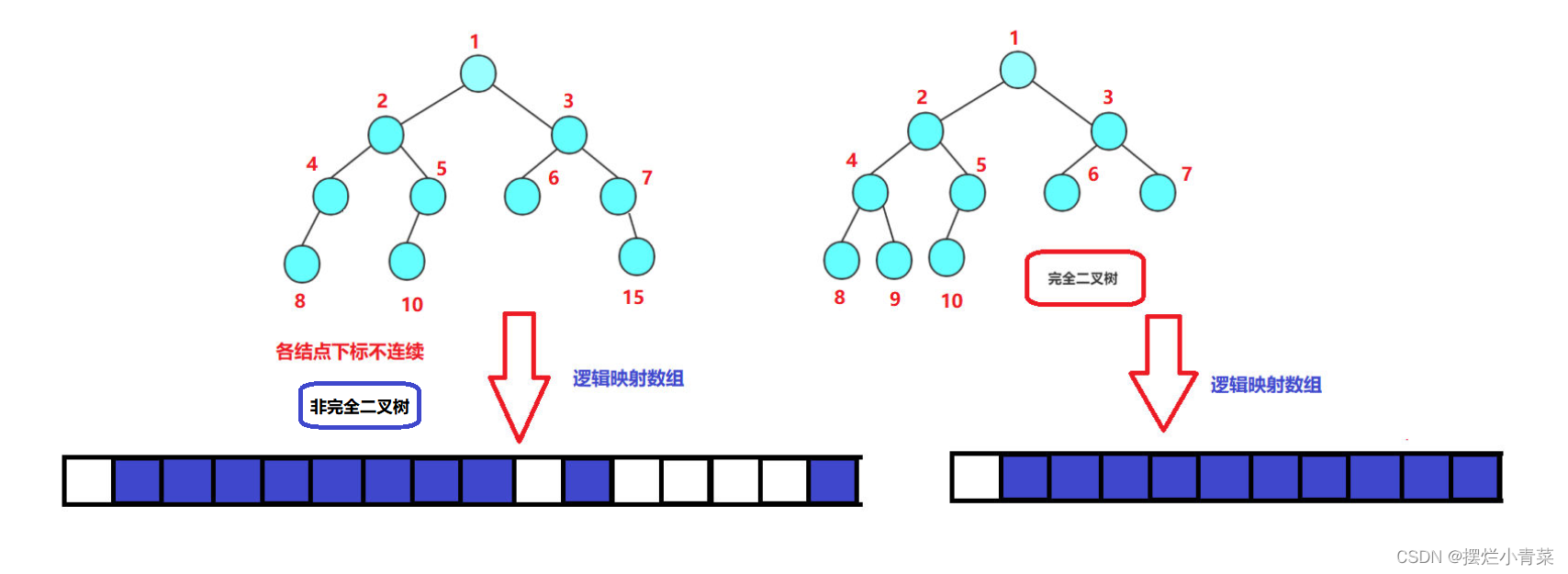
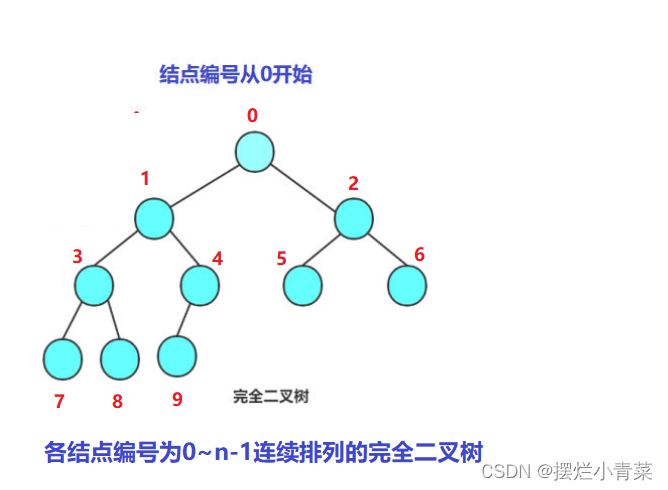
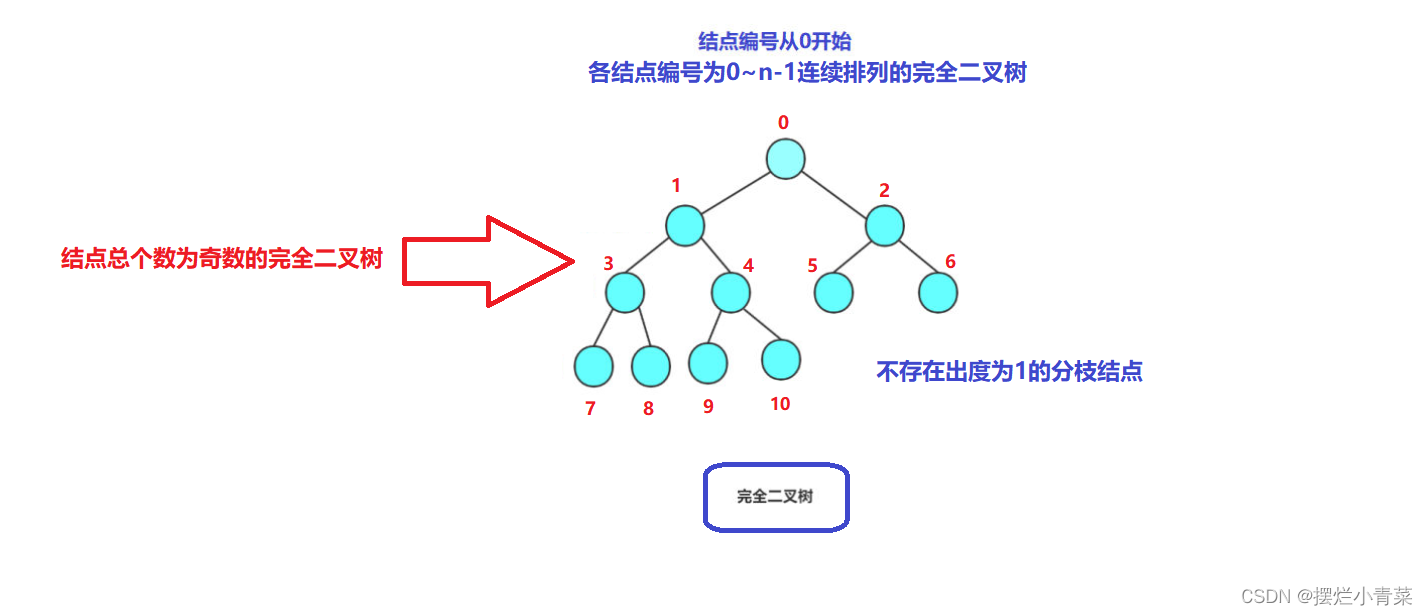
n个结点的完全二叉树的结点编号是从0~(n-1)连续排列的(假设根结点的编号为0),因此将完全二叉树映射到内存中线性存储结构中时内存利用效率十分的高(数组下标和树结点编号建立绝对映射关系).
最经典的完全二叉树线性存储结构就是大小根堆(堆排序的数据结构基础)
二.完全二叉树的重要结构特点
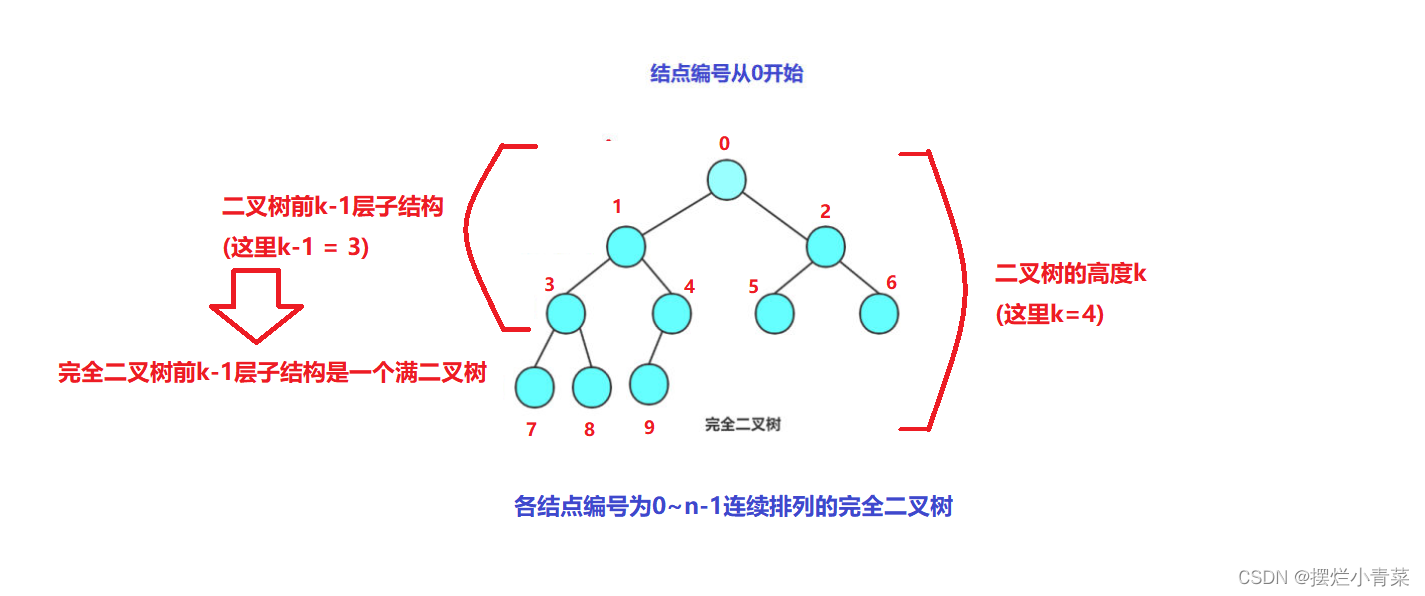
- 假设一个结点总数为n完全二叉树T的高度为k,为了满足各结点编号是0~(n-1)连续排列的结构定义,完全二叉树1~(k-1)层所有结点构成的子结构是一颗满二叉树(也就意味着完全二叉树的所有叶结点都分布在树的最后一层(第k层)):
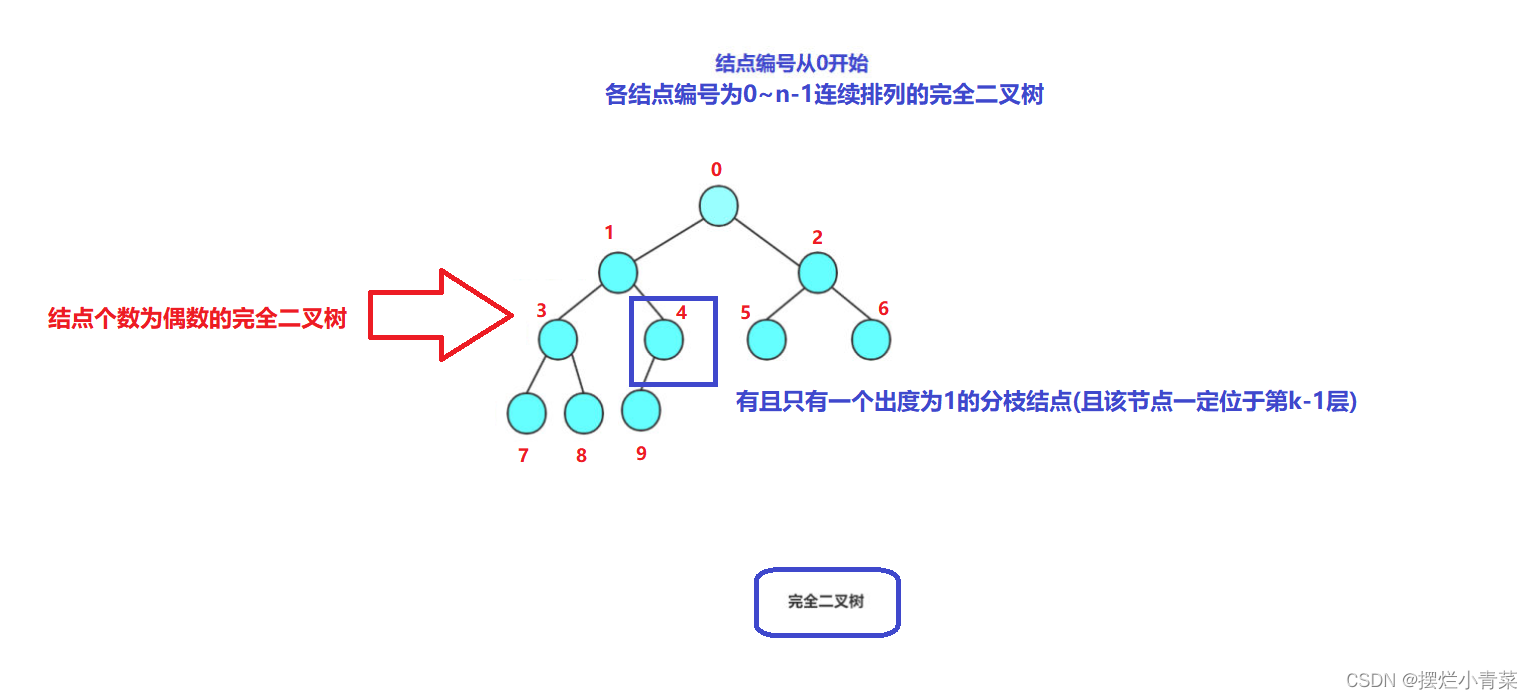
- 假设一个结点总数为n完全二叉树T的高度为k,为了满足各结点编号是0~(n-1)连续排列的结构定义,完全二叉树的第k层(最后一层)的叶节点必须是连续排列的(也就是意味着结点总数为奇数的完全二叉树不存在出度为1的分枝结点,结点总数为偶数的完全二叉树有且仅有一个出度为1的分枝结点)
三.完全二叉树开胃菜小练习
1.一个重要的数学结论
对任何一棵二叉树, 如果出度为0其叶结点个数为N0, 出度为2的分枝结点个数为N2(包括根) ,则有 N0= N2+1
该结论具体证明参见小青菜的博客 :http://t.csdn.cn/imdra
http://t.csdn.cn/imdra
2.简单的小练习
- 现有一颗具有 2n 个结点的完全二叉树T,求其叶结点的个数
求解:
设T出度为0的结点个数为N0(即叶结点的个数),
出度为1的结点个数为N1,
出度为2的结点个数为N2。
根据本篇第二章中的结构分析可知,N1要么为1,要么为0
- 若N1 = 0,根据关系式N0 = N2 + 1,可得:2n = N0 + N1 + N2,化简可得N0 = (2n+1)/2,N0不为整数,因此该种情况排除
- 若N1 =1,根据关系式N0 = N2 + 1,可得:2n = N0 + N1 + N2,化简可得N0 = n,满足题意
因此T叶节点个数为n
- 一棵完全二叉树的结点总数为531个,求这棵树的高度
求解:
设该树的高度为k
根据本篇第二章中的结构分析可知,该树前k-1层构成一颗满树(根据等比数列求和公式满树总结点个数为2^(k-1)-1)
而2^9 = 512<531<2^10 = 1024,因此k-1 = 9,可以求得该二叉树的高度为10
- 现有一颗具有767个结点的完全二树T,求其叶子结点个数
求解:
设T出度为0的结点个数为N0(即叶结点的个数),
出度为1的结点个数为N1,
出度为2的结点个数为N2。
根据本篇第二章中的结构分析可知,N1要么为1,要么为0
- 若N1 = 0,根据关系式N0 = N2 + 1,可得:767 = N0 + N1 + N2,化简可得N0 = 384,满足题意
- 若N1 =1,根据关系式N0 = N2 + 1,可得:767 = N0 + N1 + N2,化简可得N0 = 767/2,N0不为整数,因此该种情况排除
因此T叶节点个数为384

相关文章:

数据结构:完全二叉树开胃菜小练习
目录 一.前言 二.完全二叉树的重要结构特点 三.完全二叉树开胃菜小练习 1.一个重要的数学结论 2.简单的小练习 一.前言 关于树及完全二叉树的基础概念(及树结点编号规则)参见:http://t.csdn.cn/imdrahttp://t.csdn.cn/imdra 完全二叉树是一种非常重要的数据结构: n个结点的…...

mybatis与jpa
1、官方文档 mybatis:mybatis-spring – jpa:https://springdoc.cn/spring-data-jpa/ 应用文档 jpa详解_java菜鸟1的博客-CSDN博客 JPA简介及其使用详解_Tourist-xl的博客-CSDN博客_jpa的作用 2、使用比较 mybatis一般用于互联网性质的项目&#x…...

js 求解《初级算法》66. 加一
一、题目描述 给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。你可以假设除了整数 0 之外,这个整数不会以零开头。 示例 1: 输入:…...

力扣-游戏玩法分析
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:511. 游戏玩法分析二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总结…...
(附完整源码))
ZZNUOJ_用C语言编写程序实现1186 : 奖学金(结构体专题)(附完整源码)
题目描述 某校发放奖学金共5种,获取条件各不同: 1.阳明奖学金,每人8000,期末平均成绩>80,且在本学期发表论文大于等于1篇; 2.梨洲奖学金,每人4000,期末平均成绩>85,且班级评议成绩>80; 3.成绩优秀奖,每人2000,期末平均成绩>90; 4.西部奖学金,…...

加油站ai系统视频监测 yolov5
加油站ai系统视频监测通过yolov5网络模型深度学习边缘计算技术,加油站ai系统视频监测对现场卸油过程中人员违规离岗、现场灭火器没有按要求正确摆放、以及卸油前需要遵守静电释放15分钟、打电话、明火烟雾情况、抽烟行为进行自动识别。YOLO系列算法是一类典型的one-…...
【JDK8新特性之Stream流-Stream结果收集案例实操】
一.JDK8新特性之Stream流-Stream结果收集以及案例实操 二.Stream结果收集(collect函数)-实例实操 2.1 结果收集到集合中 /*** Stream将结果收集到集合中以及具体的实现 collect*/Testpublic void test01(){// 收集到List中 接口List<Integer> list Stream.of(1, 2, 3…...

Fiddler 抓包工具
HTTP代理所谓的http代理,其实就是代理客户机的http访问,主要代理浏览器访问页面。代理服务器是介于浏览器和web服务器之间的一台服务器,有了它之后,浏览器不是直接到Web服务器去取回网页而是向代理服务器发出请求,Requ…...
2023最新版网络安全保姆级指南,手把手带你从零基础进阶渗透攻防工程师
前言 一份网络攻防渗透测试的学习路线,不藏私了! 1、学习编程语言(phpmysqljshtml) 原因: phpmysql可以帮助你快速的理解B/S架构是怎样运行的,只有理解了他的运行原理才能够真正的找到问题/漏洞所在。所以对于国内那些上来就说…...
排序基础之选择排序法
目录 前言 一、什么是选择排序 二、实现选择排序 三、使用泛型扩展 四、使用自定义类型测试 前言 今天天气不错,这么好的天气不干点啥实在是有点可惜了,于是乎,拿出键盘撸一把! 来,今天来学习一下排序算法中的选…...

2.24测试用例
一.测试模型1.V模型特点:1.明确标注了测试的类型2.明确标注了测试阶段和开发阶段的对应关系缺点:测试后置2.W模型也叫双v模型,测试阶段全流程介入缺点:1.上一阶段完成.下一个阶段才能开始2.开发模型和测试模型也保持着一种线性的前后关系3.重文档,重过程,不支持敏捷模式二.设计…...

面试必刷101 Java题解 -- part 1
练习地址 面试必刷101-牛客1、链表反转2、链表内指定区间反转**3. 链表中的节点每k个一组翻转**4、**合并两个排序的链表**5、**合并k个已排序的链表**6、**判断链表中是否有环****7、链表中环的入口结点**8、链表中倒数最后k个结点**9、删除链表的倒数第n个节点****10、两个链…...
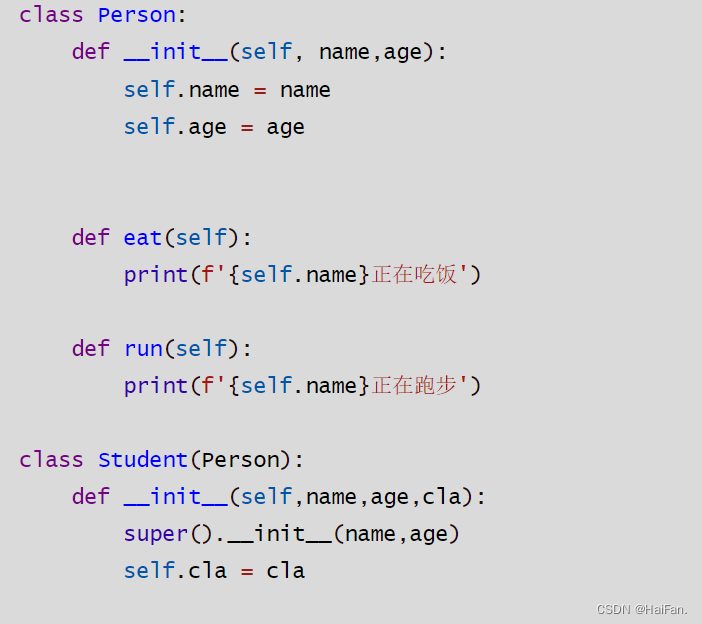
Python---关联与继承
专栏:python 个人主页:HaiFan. 专栏简介:Python在学,希望能够得到各位的支持!!! 关联与继承前言has a关联关系is a继承关系子类不添加__init__子类添加__init__前言 has a关联关系 has - a 是在…...
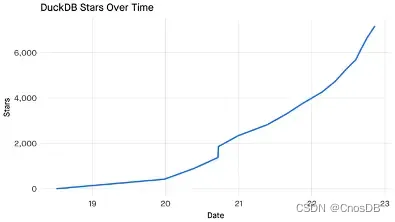
数据库行业的 “叛逆者”:大数据已“死”,MotherDuck 当立
“大数据”已死——现今我们最重要的事情不是担心数据大小,而是专注于我们将如何使用它来做出更好的决策。数据库行业发展至今,在数据层面有很多的加速和变革,尤其是过去几年的云数仓爆炸式增长,带来了行业的很多变化。毫无疑问&a…...

Linux->进程优先级
目录 1. 优先级的概念 2. 优先级的运作方式 3. Linux下查看进程优先级以及调整 3.1 查看进程优先级 3.2 修改进程优先级 1. 优先级的概念 1. cpu资源分配的先后顺序,就是指进程的优先权(priority)。 2. 优先权高的进程有优先执行权利。配…...
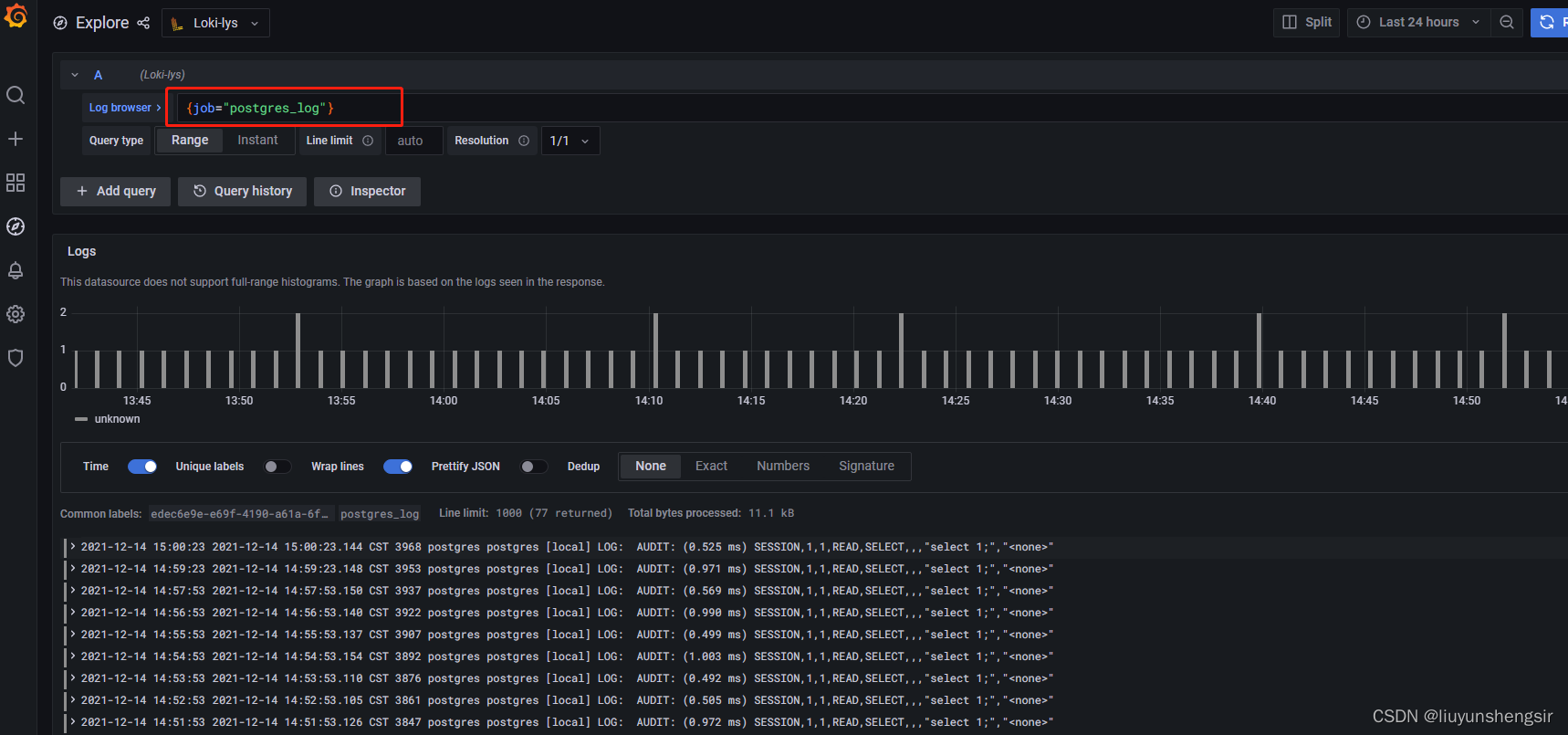
loki 日志管理的安装部署使用
loki介绍 Loki是 Grafana Labs 团队最新的开源项目,是一个水平可扩展,高可用性,多租户的日志聚合系统。它的设计非常经济高效且易于操作,因为它不会为日志内容编制索引,而是为每个日志流编制一组标签。 不对日志进行…...

CTFer成长之路之反序列化漏洞
反序列化漏洞CTF 1.访问url: http://91a5ef16-ff14-4e0d-a687-32bdb4f61ecf.node3.buuoj.cn/ 点击下载源码 本地搭建环境并访问url: http://127.0.0.1/www/public/ 构造payload: ?sindex/index/helloðanwhoamiPOST的参数&#…...

Python学习-----模块5.0(文件管理大师-->os模块)
目录 前言: 1.os.getcwd() 2. os.listdir(path) 3.os.walk(path) 4.os.path.exists(path) 5.os.mkdir(path) 6.os.makedirs(path,exist_okTrue) 7.os.rmdir(path) 8.os.remove(path) 9.os.path.join(p1,p2) 10.os.path.split(path) 11.os.path.isdi…...
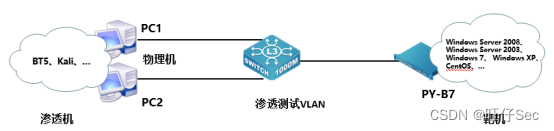
第45届世界技能大赛“网络安全”赛项浙江省选拔赛竞赛任务书
第45届世界技能大赛浙江省选拔赛竞赛任务书 一、竞赛时间 8:00-17:00,共计9小时。 二、竞赛阶段 竞赛阶段 任务阶段 竞赛任务 竞赛时间 分值 模块A 任务1 数据库安全加固 8:00-10:00 50 任务2 文件MD5校验 50 任务3 Linux系统服务渗透测试及安全加…...
【uniapp微信小程序】跨平台使用echarts的方案选择踩坑
一、前言 使用Uniapp(vue)开发微信小程序,想用echarts图表实现类似github热力图的效果。 简要列一些可行或不可行的方案。 二、方案对比 1. 【应用】:微信小程序原生开发 有echarts官网提供的跨平台方案:在微信小程…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...