【数据结构】——二叉树的基础知识
数概念及结构
数的分类
二叉树、多叉树
数的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限节点组成一个具有层次关系的集合。把它叫做树的原因是它看起来像一颗倒挂的树,也就是说它是跟朝上,而叶朝下的。
- 有一个特殊的节点,称为根节点,这个节点没有前驱节点。
- 除根节点外,其余节点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<=i<=m)又是一颗结构与树类似的子树。每颗子树的根节点有且只有一个前驱,可以有0个或多个后继节点。
- 数是递归定义的。
- 子树是不相交的;
什么是递归:
大问题->类似子问题->类似子问题
数的相关概念
结点的度: 一个结点含有的子树的个数称为该结点的度。
叶结点或终端结点:度为0的结点。
非终端结点或分支结点:度不为0的结点。
双亲结点或父节点:若一个结点含有子结点,则这个结点称为其子结点。
孩子节点或父节点:一个节点含有子树的根的节点称为该节点的子节点。
兄弟节点:具有相同父节点的节点称为兄弟节点。
树的度:一个树中最大的节点的度称为树的度。
节点的层次:从跟开始定义起,根为第1层,根的子节点为第二层。
树的高度或深度:树中节点的最大层次。
堂兄弟节点:双亲在同一层次的节点互为堂兄弟。
节点的祖先:从根到该节点所经分支上的所有节点。
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
森林:由m(m>0)颗互不相交的树的集合称为森林。
数的高度一般都是从1开始,从0开始也可以。
扩展:
数组下标为什么要从0开始,因为这符合偏移量。
当前元素到第一个元素的偏移量,第一个元素的下标自然就是0,第二个元素的下标为1,第n个元素的下标为n-1。
并查集里面就是多棵树。
数的存储
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既要保存值域,也要保存节点和节点之间的关系,实际中树有很多的表示方式如:双亲表示法、孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里简单的了解其中最常见的孩子兄弟表示法。
struct TreeNode
{int val;struct TreeNode* firstchild;struct TreeNode*nextbrother;
}
数在实际中的运用(表示文件系统的目录结构)
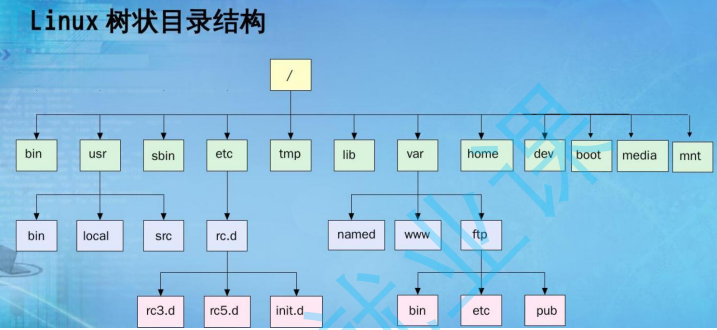
文件系统就是一个树形结构。
还有一种双亲表示法:只存储双亲的下标或指针。
两个结点在不在同一棵树,如何判断?
找根,根相同就是在同一棵树。
二叉树概念及结构
概念
一颗二叉树是结点得一个有限集合,该集合:
1、或者为空
2、由一个根结点加上两颗别称为左子树和右子树得二叉树组成。
注意:
1、二叉树最多两个孩子。
2、二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
注意:
空树、只有根结点、只有左子树、只有右子树、左右子树均存在。
特殊的二叉树
满二叉树
每一层都是2^(i-1)个结点,每一层都是满的就是满二叉树。
高度为h的满二叉树有多少个节点:
F(h)=20+21+…+2(h-2)+2^(h-1)
使用错位相减法可以得到下面的结果
F(h)=2^h-1

完全二叉树
假设他的高度是h,前h-1层是满的,最后一层不一定满,从左到右是连续的。

二叉树的性质
1、若规定根节点的层数为1,则一颗非空二叉树的第i层上最多有2^(i-1)个节点。
2、若规定根节点的层数为1,则深度为h的二叉树的最大节点数是2^k-1.
3、在任何二叉树中,度为0的叶子节点永远比度为2的多一个,只有一个节点时 n0=n2+1。
完全二叉树特点:
度为1的节点只有1个或者0个。如果节点的个数是偶数那么度为1的节点个数等于1,反之则为0。
二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只合适表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
以下是数组结构存储的特点:
leftchild=parent * 2+1;
rightchild=parent*2+2;parent=(child-1)/2;
任意位置通过下标可以找到父亲或者孩子。
总结:满二叉树和完全二叉树适合使用数组储存。
链式存储
二叉树的链式存储结构是指,用链表来表示一颗二叉树,即用链来指示元素的逻辑关系。通常的方法是每个链表中每个节点由三个域组成,数据域和左右指针域,左右指针分别用来表示给出该节点左孩子和右孩子所在的链节点的存储地址。
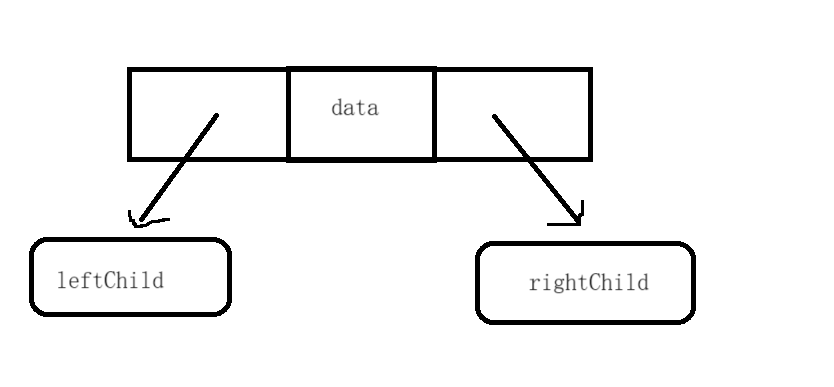
结构如下
typedef int BTDataType;
struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode*right;BTDataType data;
}
二叉树顺序结构及实现
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。实现中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
堆的概念
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或者小堆根。
堆:非线性结构,完全二叉树
小堆:树中任意一个父亲都<=孩子
大堆:树中任意一个父亲都>=孩子
底层:物理结构,数组
逻辑结构,完全二叉树
小堆,底层数组是否升序呢?不一定。
小堆的根是整棵树的最小值。可以解决的问题:
1、topk问题
2、堆排序
堆的实现
堆的插入
插入数据之后还要保证数据是堆。
堆的定义
底层就是一个顺序表,可以使用数组来存储。
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
堆的初始化HeapInit
1)断言
2)有两种方式第一种直接置空,第二种开一个空间。
//初始化堆
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}
打印HeapPrint
1)断言
2)使用循环打印
//打印
void HeapPrint(HP* php)
{assert(php);for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}
释放空间HeapDestroy
1)断言
2)先释放数组
//释放空间
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}
向上调整AdjustUp
1)先算出父节点
2)使用child等于0来结束循环
3)判断孩子节点是否小于父节点,小于的话就交换,同时要修改child和parent的大小
4)反之,则直接退出循环。
void AdjustUp(HPDataType* a, int child)
{//找到父节点int parent = (child - 1) / 2;//当下标小于等于零的时候结束循环while (child>0){if (a[child]<a[parent]){//交换两个数Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{//直接跳出循环break;}}
}
交换函数Swap
需要的参数就是两个指针。
根据传过来的指针,直接交换就好。
void Swap(HPDataType* child, HPDataType* parent)
{int temp = *child;*child = *parent;*parent = temp;
}
插入数据HeapPush
1)断言
2)扩容
3)使用realloc在堆上开辟空间。
4)向上调整,向上调整的时候是需要数组的指针和最后一个数的下标
//插入数据
void HeapPush(HP* php, HPDataType x)
{assert(php);//扩容if (php->size==php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* temp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (temp==NULL){perror("realloc fail");exit(-1);}//把创建的空间分配给aphp->a = temp;//定义容器的大小php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a,php->size-1);
}
向下调整AdjustDown
需要的参数指向数组的指针,元素的个数,跟节点的下标。
1)先找到孩子
使用循环来找孩子,循环的结束条件就是孩子的下标小于元素个数
2)比较两个孩子谁小一点
注意右孩子可能出现越界的情况这需要考虑
3)再比较孩子节点和父节点上的值
如果比父节点上的值小那就交换,再继续向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){if (child+1<n&&a[child+1]<a[child]){child++;}if (a[child]<a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
删除数据HeapPop
删除根比较有意义。
如果挪动覆盖第一个位置根,关系全乱了。
1)先交换 根和最后一个值交换,再删除。
需要注意的是要控制size的大小因该控制在大于0
交换完之后size需要减1
2)向下调整
传参数的时候要传3个参数,数组,元素个数,根节点。
元素个数用来控制节点的最大下标。
//删除数据
void HeapPop(HP* php)
{//断言assert(php);assert(php->size>0);//交换Swap(&php->a[0], &php->a[php->size - 1]);php->size--;//向下调整AdjustDown(php->a,php->size,0);
}
堆顶的数据HeapTop
只需要堆的指针
1)断言
是否为空指针,是否为空堆
2)返回根
//取堆顶的数据
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
初始化数组HeapInitArray
需要的参数堆的指针,数组指针,开的空间大小
1)断言
判断两个指针是否为空指针。
2)给数组开空间
并判断空间是否开辟完成
3)使用memcpy函数进行复制
4)建堆
//初始化数组
void HeapInitArray(HP* php, int* a, int n)
{assert(php);assert(a);php->a = (HPDataType*)malloc(sizeof(HPDataType)*n);if (php->a==NULL){perror("malloc fail");exit(-1);}php->size = n;php->capacity = n;memcpy(php->a, a, sizeof(HPDataType) * n);for (int i = 0; i < n; i++){AdjustUp(php->a, i);}
}
判空HeapEmpty
只需要堆的指针
1)断言
看指针是否为空
2)返回size是否等于0
//判空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}使用堆排序HeapSort
堆排序的特点:就是数组有序
缺点:需要写有一个堆。
向上调整。
排升序,建大堆。
堆顶跟最后一个位置交换,最大的数据就排好了,剩下数据向下调整,选出次大的,代价是logN。合计是:N* logN
//void HeapSort(int* a, int n)
//{
// HP hp;
// //初始化
// HeapInit(&hp);
//
// for (int i = 0; i < n; i++)
// {
// HeapPush(&hp, a[i]);
// }
//
// int i = 0;
// while (!HeapEmpty(&hp))
// {
// printf("%d ", HeapTop(&hp));
// a[i++] = HeapTop(&hp);
// HeapPop(&hp);
// }
//
// HeapDestroy(&hp);
//}void HeapSort(int* a, int n)
{// 建堆 (大堆)or (小堆)for (int i = 1; i < n; i++){AdjustUp(a, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}}
void test2()
{int a[] = { 2,3,5,7,4,6,8 };HeapSort(a, sizeof(a) / sizeof(int));
}
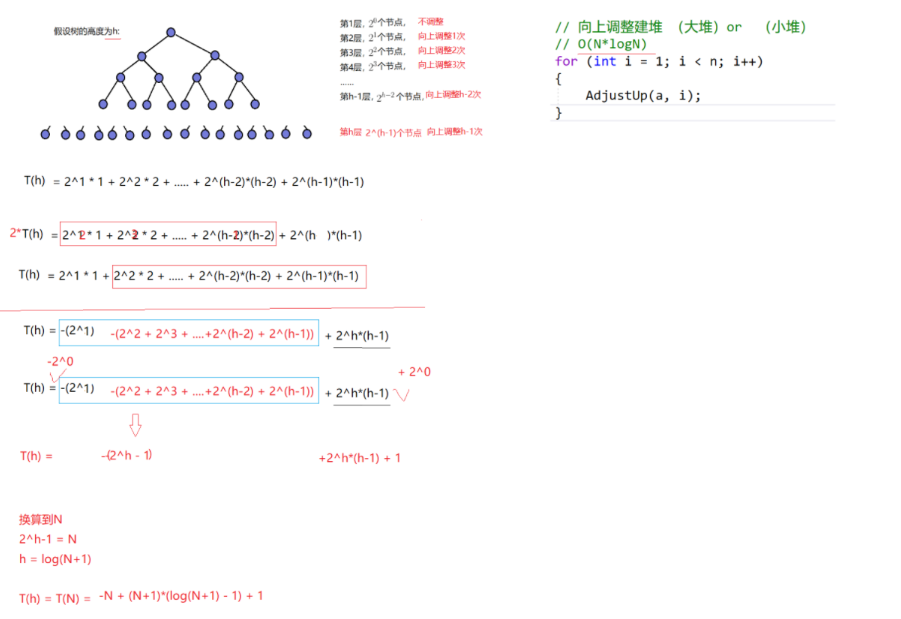
向下调整建堆

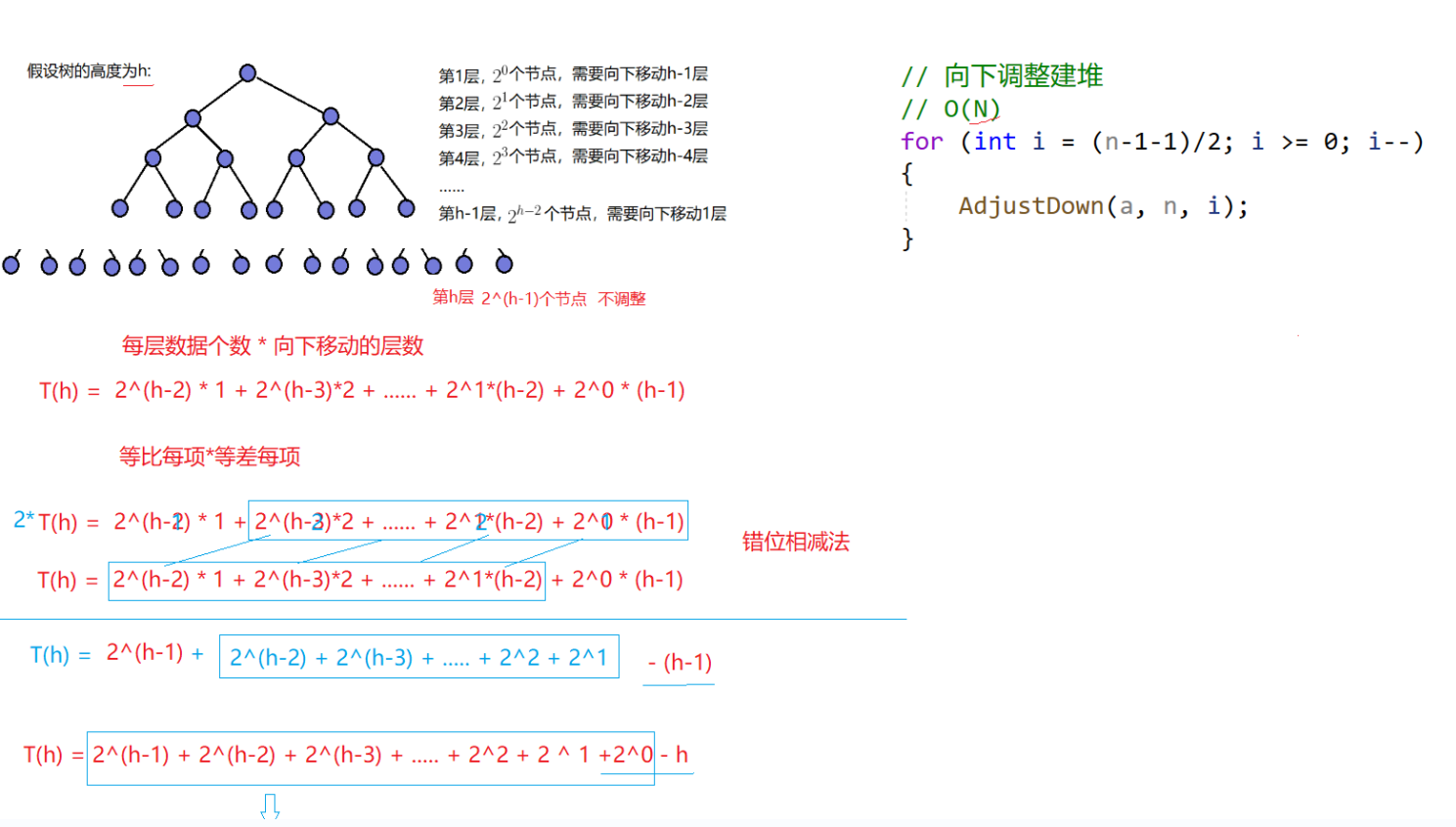
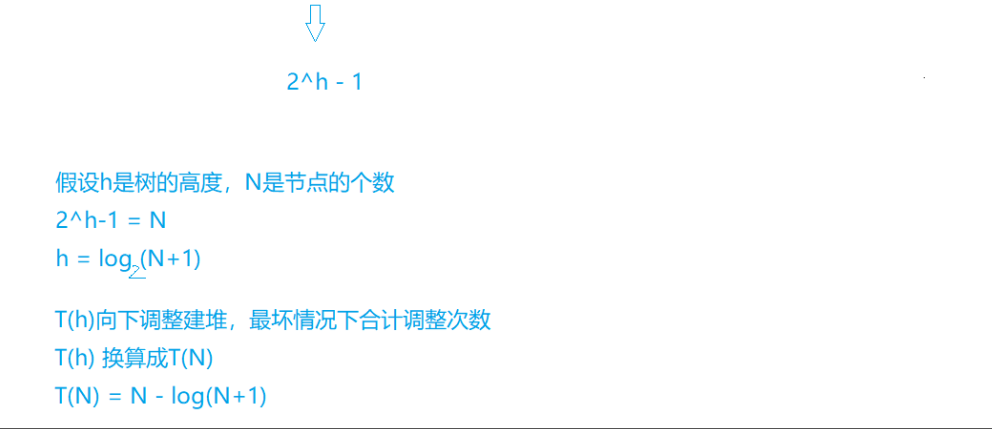
向上调整
TopK问题
假设10亿个数据,内存存不下,数据在文件中找出最大的前k个。
1、读取文件的前100个数据,在内存中建立小堆
2、再依次读取剩下数据,跟堆顶数据比较,大于堆顶,就替换他进堆,向下调整
3、所有的数据读完,堆里面数据就是最大的前100个
核心:
建立小堆、时间复杂度:O(N* logK)、空间复杂度:O(K)
void PrintTopK(const char* filename, int k)
{// 1. 建堆--用a中前k个元素建堆FILE* fout = fopen(filename, "r");if (fout==NULL){perror("fopen fail");return;}int* minheap = (int*)malloc(sizeof(int) * k);if (minheap==NULL){perror("malloc fail");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);}//前k个数建小堆for (int i = (k-2)/2; i >=0 ; i--){AdjustDown(minheap, k, i);}// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换int x = 0;while (fscanf(fout,"%d",&x)!=EOF){if (x>minheap[0]){//替换进堆minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");free(minheap);fclose(fout);
}//创建文件
void CreateNData()
{//造数据int n = 1000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin==NULL){perror("fopen error");return;}for (int i = 0; i < n; i++){int x = (rand() + i) % 1000000;fprintf(fin, "%d\n", x);}fclose(fin);
}int main()
{//CreateNData();PrintTopK("data.txt", 5);return 0;
}
二叉树链式结构及实现
二叉树的遍历(递归遍历)

普通的链式二叉树没有意义。
1、更复杂二叉树搜索树->AVL 红黑树(以后打基础)
2、很多二叉树的题,是出这一块
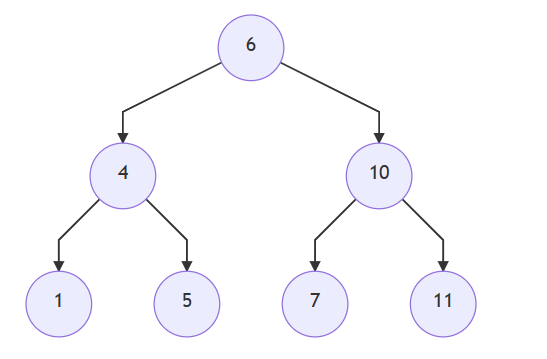
这就是搜索二叉树,左边比根小右边比根大。
搜索二叉树走中序就是排序。
前序遍历PrevOrder
1、先手动构建二叉树
typedef struct BinaryTreeNode
{struct BinaryTreeNode*left;struct BinaryTreeNode*right;int val;
}BTNode;BTNode*BuyNode(int x)
{BTNode*node=(BTNode*)malloc(sizeof(BTNode));if(node==NULL){perror("malloc fail");return;}node->val=x;node->left=NULL;node->right=NUll;return node;
}
2、手动链接
int main()
{BTNode* node1=BuyNode(1);BTNode* node2=BuyNode(2);BTNode* node3=BuyNode(3);BTNode* node4=BuyNode(4);BTNOde* node5=BuyNode(5);BTNode* node6=BuyNode(6);node1->left=node2;node1->right=node4;node2->left=node3;node4->left=node5;node4->right=node6;return 0;
}
3、根 左子树 右子树
void PrevOrder(BTNode*root)
{if(root==NULL){printf("NULL ");return ;}printf("%d ",root->val);PrevOrder(root->left);PrevOrder(root->right);
}
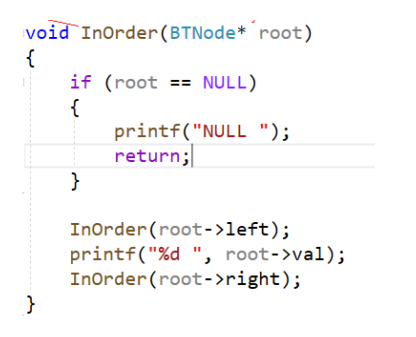
中序遍历InOrder
先左子树 根 右子树
void InOrder(BTNode*root)
{if(root==NULL){printf("NULL ");return ;}InOrder(root->left);printf("%d ",root->val);InOrder(root->right);
}
后序遍历PostOrder
先左子树 右子树 根
void PostOrder(BTNode*root)
{if(root==NULL){printf("NULL");return ;}PostOrder(root->left);PostOrder(root->right);printf("%d ",root->val);
}
二叉树节点个数TreeSize
方法一:简单的方式就是遍历一遍。
方法二:当前节点的个数等于左子树+右子树+自己
1、当前为空的时候返回0
2、反之就返回左子树+右子树+1
int TreeSize(BTNode* root)
{return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
叶子节点个数TreeLeafSize
1、空->0
2、叶->1
3、左子树+右子树
int TreeLeafSize(BTNode*root)
{if(root==NULL){return 0;}if(root->left==NULL&&root->right==NULL){return 1;}return TreeLeafSize(root->left)+TreeLeafSize(root->right);
}
第k层的节点个数TreeLevel
1、当前树的第k层=左子树的第k-1层+右子树的第k-1层
int TreeLevel(BTNode*root,int k)
{if(root==NULL){return 0;}if(k==1){return 1;}return TreeLevel(root->left,k-1)+TreeLevel(root->right,k-1);
}
二叉树的销毁TreeDestroy
1、子问题
2、返回条件(最小规模的子问题)
3、使用后序遍历的思想进行销毁
void TreeDestroy(BTNode* root)
{if (root==NULL){return;}TreeDestroy(root->left);TreeDestroy(root->right);free(root);
}
二叉树查找值为X的节点TreeFind
BTNode* TreeFind(BTNode* root, int x)
{//如果是空者返回空指针if (root==NULL){return NULL;}//如果找到了就返回当前节点的指针if (root->val==x){return root;}//定义一个指针来接受返回的地址BTNode* ret = NULL;//返回左边ret=TreeFind(root->left, x);//看左边是否为空,不为空就说明找到了,直接返回给上一级地址if (ret){return ret;}ret = TreeFind(root->right, x);//看右边是否为空,不为空就说明找到了,直接返回给上一级地址if (ret){return ret;}//要是走到这个位置也没有返回说明没有找到值return NULL;
}层序遍历(LevelOrder)
上一层带下一层
先进先出。
void LevelOrder(BTNode* root)
{//首先初始化Que q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){//取头的数据BTNode* front = QueueFront(&q);printf("%d ", front->val);//带入左右子树if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}QueuePop(&q);}printf("\n");
}
优先遍历
深度优先遍历(DFS)
前序遍历
广度优先遍历(BFS)
层序遍历,配合队列
相关文章:

【数据结构】——二叉树的基础知识
数概念及结构 数的分类 二叉树、多叉树 数的概念 树是一种非线性的数据结构,它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做树的原因是它看起来像一颗倒挂的树,也就是说它是跟朝上,而叶朝下的。 有一个特殊的节点&…...

日常bug汇总
1.constraintlayout NestedScrollView 可能会导致NestedScrollView 不滑动 2.截屏 open class SecureFragment : LogLifecycleFragment() {override fun onResume() {super.onResume()if (!BuildConfig.DEV) {requireActivity().window.setFlags(WindowManager.LayoutParam…...
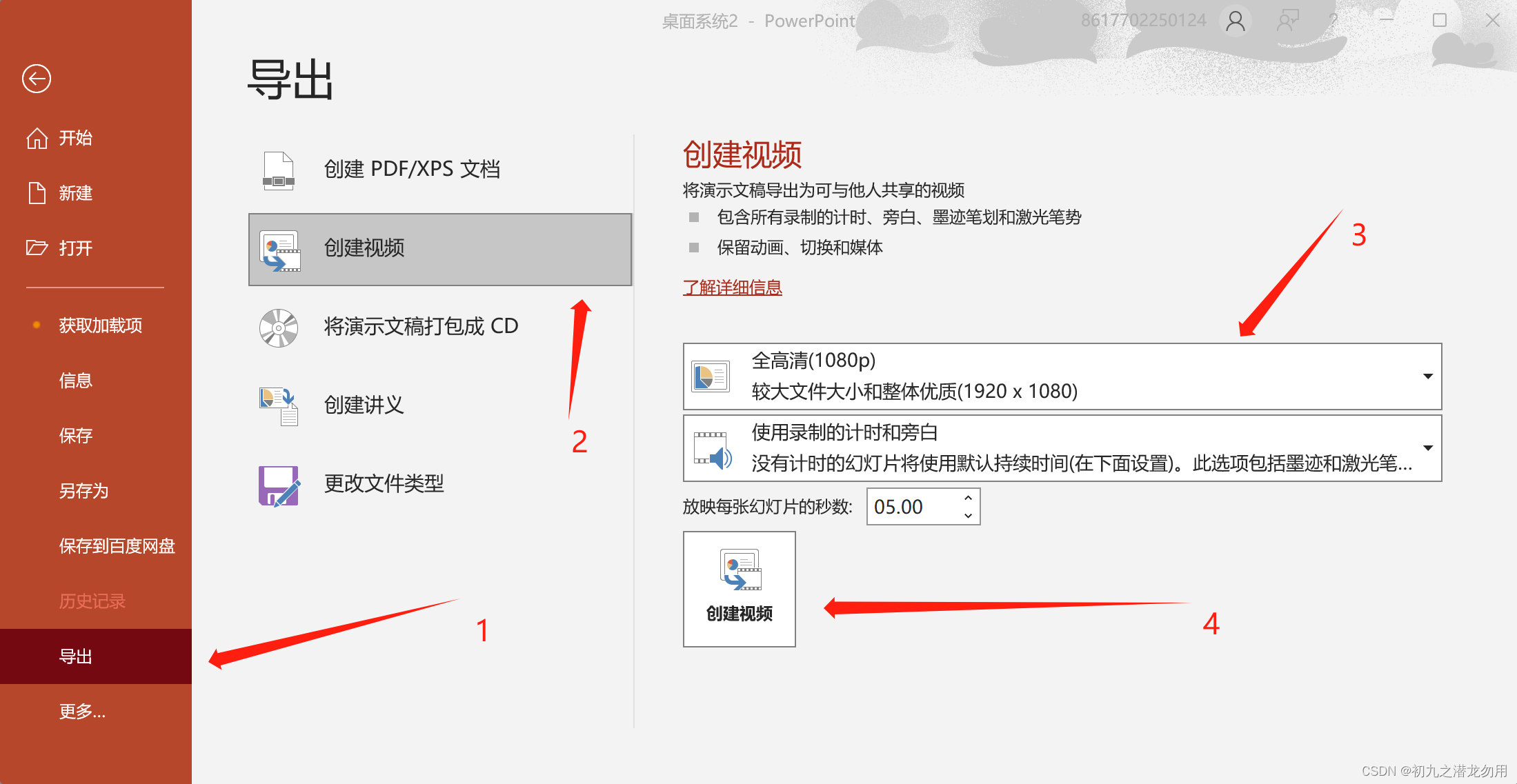
C#使用PPT组件的CreateVideo方法生成视频
目录 需求 实现 CreateVideo方法 关键代码 CreateVideoStatus 其它 需求 我们在使用PowerPoint文档时,经常会使用其导出功能以创建视频,如下图: 手工操作下,在制作好PPT文件后,点击文件 -> 导出 -> 创建视…...
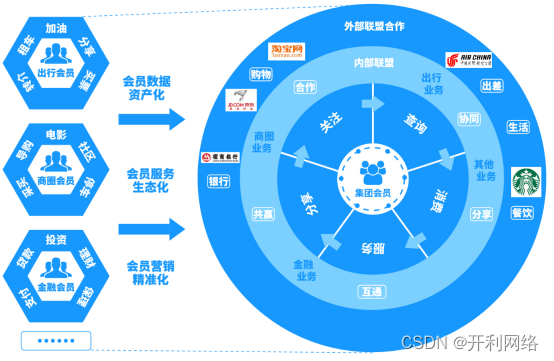
数字化体系如何帮助企业拓展裂变增长渠道?数字化营销体系构建?
在当前的商业环境中,数字不仅仅是数据,还代表着技术和资产。企业数字化正是将数据转化为资产的过程。从信息化时代到数字化时代,企业逐渐将业务和组织、管理和创收都朝着在线化和数据化的方向发展,特别是企业的业务板块。数字化营…...
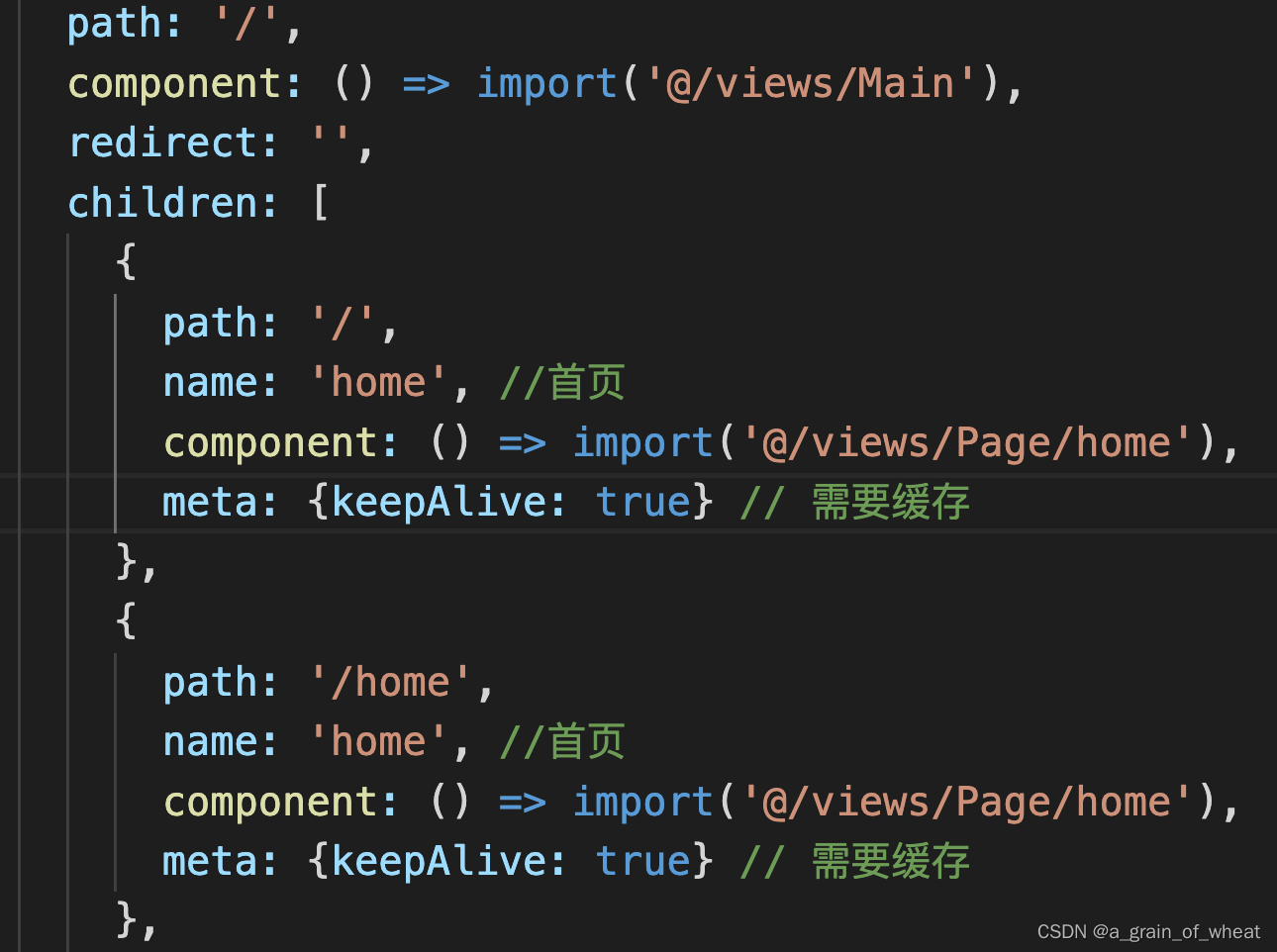
关于vant 的tabbar功能
1、想要实现tabbar页面A,其他的页面B(非tabbar页面)。 从A页面进入B页面,底部的active选中效果应该被取消掉,但是还是选中A。 按照官网的说法有两个方法 一、根据path路径 二、自定义的model 但是!但是…...

:style动态绑定,但只要页面发生变化就会执行一次方法
1、问题 开发过程中有个需求是遍历列表绘制div,div的样式是后端接口传来的,一开始这种写法,:style“formatStyle(item)”,写在了模板中 这样写发现一个问题,只要页面发生重绘,比如页面输入框输入数字&…...
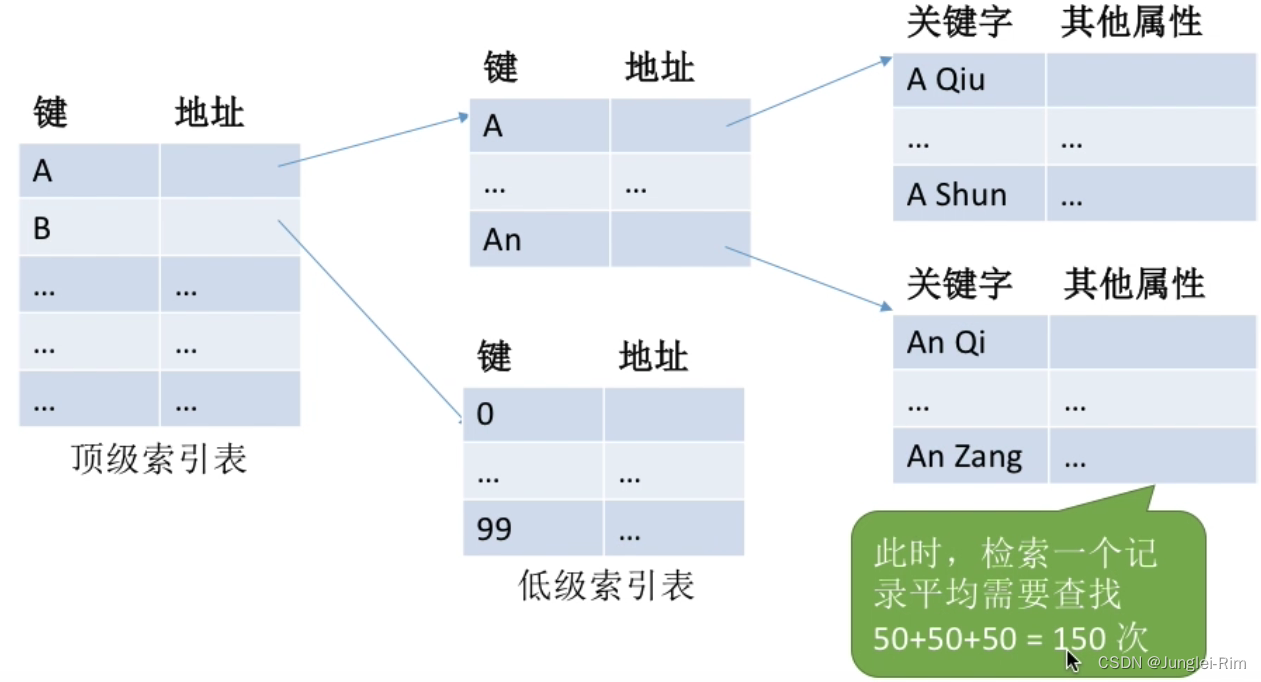
文件的逻辑结构(顺序文件,索引文件)
所谓的“逻辑结构”,就是指在用户看来,文件内部的数据应该是如何组织起来的。 而“物理结构”指的是在操作系统看来,文件的数据是如何存放在外存中的。 1.无结构文件 无结构文件:文件内部的数据就是一系列二进制流或字符流组成。无明显的逻…...

suricata匹配从入门到精通(五)----二次开发保护规则库
0x00 背景 开源的suricata资源包是没有做加密处理,如果想要保护资源包,需要二次开发修改suricata源码。 本文基于suricata6.0.1 版本https://github.com/OISF/suricata/archive/refs/tags/suricata-6.0.1.zip二开。 0x01 实践 通过debug,跟规则处理相关需要修改2个地方。…...
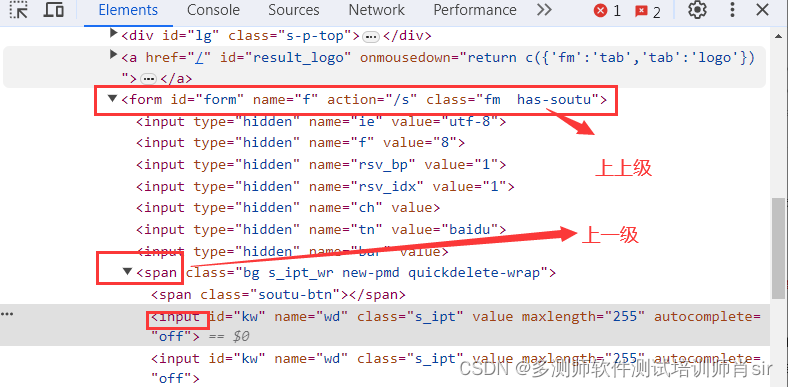
软件测试肖sir__python之ui自动化定位方法(2)
Selenium中元素定位方法 一、定位方法 要实现UI自动化,就必须学会定位web页面元素,Selenium核心 webdriver模块提供了9种定位元素方法: 定位方式 提供方法 id定位 find_element_by_id() name定位 find_element_by_name() class定位 find_elem…...
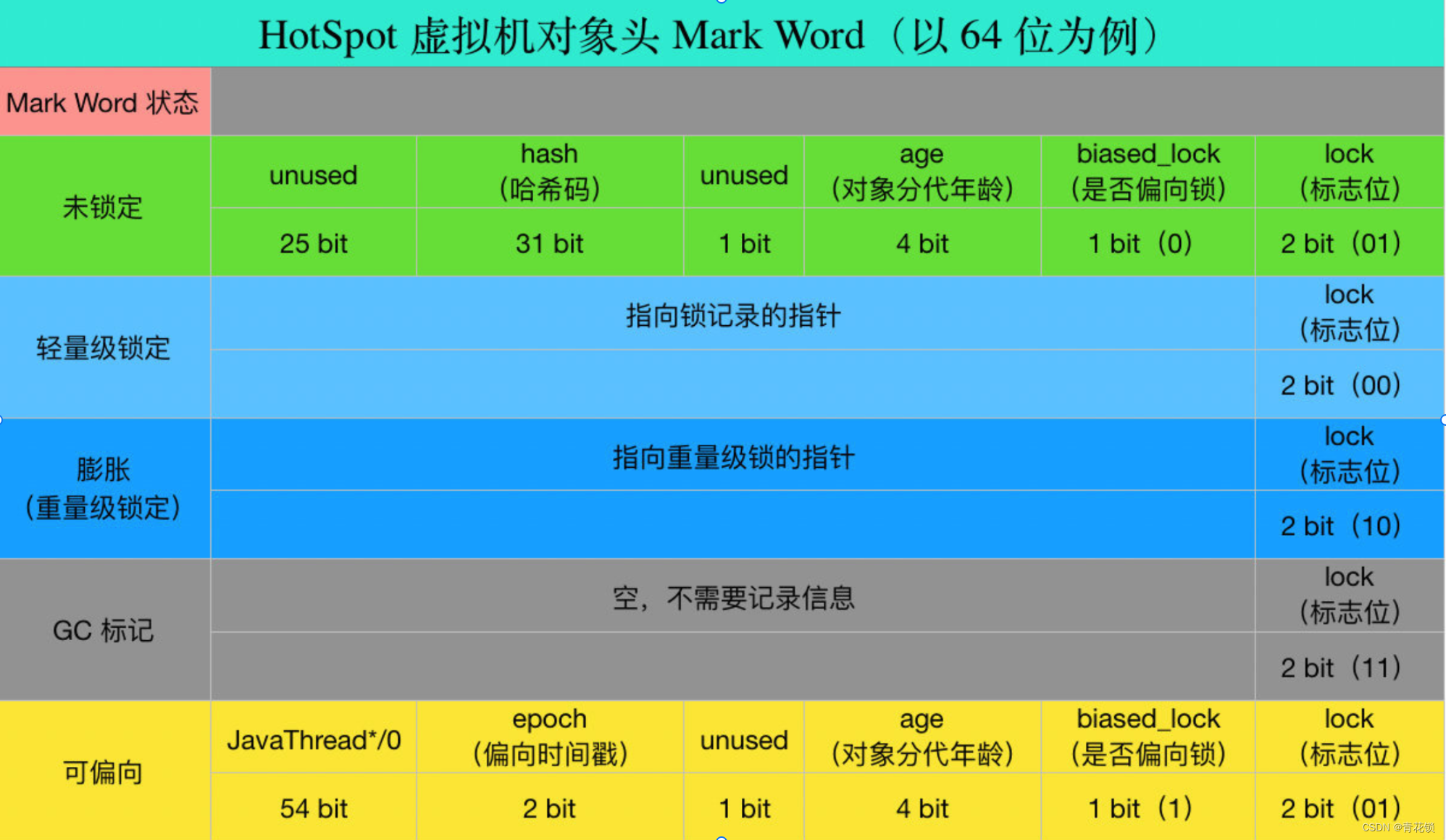
【JVM面试题】JVM分代年龄为何是15次?能设置为16吗?
系列文章目录 【JVM系列】第一章 运行时数据区 【JVM面试题】第二章 从JDK7 到 JDK8, JVM为啥用元空间替换永久代? 【JVM面试题】第三章 JVM分代年龄为何是15次?能设置为16吗? 大家好,我是青花。拥有多项发明专利(都是…...

java三层架构/表现层-业务层-持久层
三层架构 什么是 Java 三层架构 三层架构是指:视图层view(表现层),服务层service(业务逻辑层),持久层Dao(数据访问层), Java的三层架构是指将Java程序分为三…...

视频监控这样做,简单又高效!
随着技术的不断进步,视频监控系统已经变得更加高效和智能,可以提供更全面的监控和分析功能,有助于提高安全性、管理效率和决策支持。 客户案例 超市连锁店 福建某全国性超市连锁店面临高额商品损失、偷窃问题,以及对客户安全和员工…...

掌握 Go 的计时器
简介 定时器是任何编程语言的重要工具,它允许开发人员在特定时间间隔安排任务或执行代码。在 Go 中,定时器是通过 time 包实现的,该包提供了一系列功能来创建、启动、停止和有效处理定时器。我们将探索 Go 中定时器的强大功能,并…...
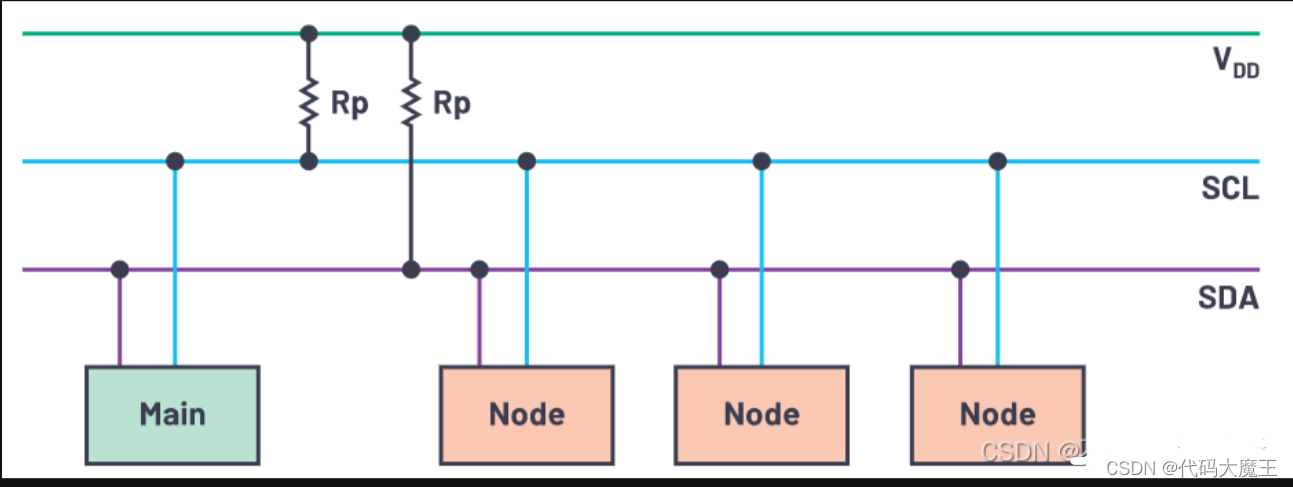
嵌入式软件开发笔试面试
C语言部分: 1.gcc的四步编译过程 1.预处理 展开头文件,删除注释、空行等无用内容,替换宏定义。 gcc -E hello.c -o hello.i 2.编译 检查语法错误,如果有错则报错,没有错误则生成汇编文件。 gcc -S hello.i -o h…...
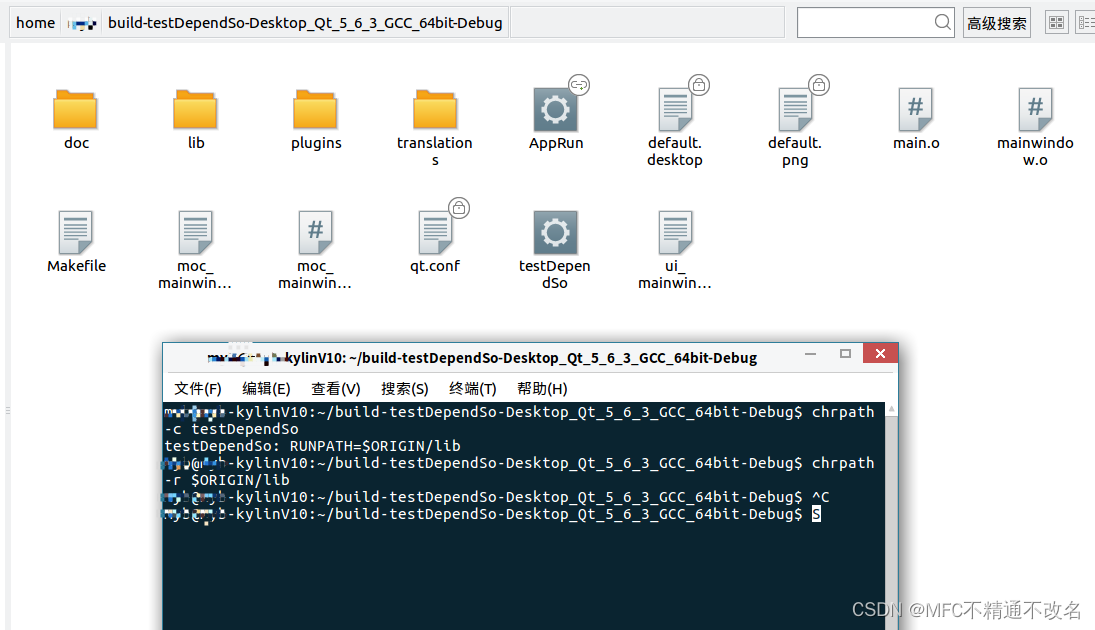
【Qt高阶】Linux安装了多个版本的Qt 部署Qt程序,出包【2023.10.17】
简介 linux系统下可执行程序运行时会加载一些动态库so,有一些是Qt的库,Qt的库会加载其他更基础的库。最后出包的时候需要把依赖的包整理到一个文件夹,来制作安装包。近期遇到已经将依赖的so文件拷贝至程序目录下,但还是调系统路径…...

OpenGL简介
OpenGL 本身并不是一个 API,它仅仅是一个由 Khronos组织 制定并维护的规范(Specification)。规范严格规定了每个函数该如何执行,以及它们的输出值。至于内部具体每个函数是如何实现的,将由 OpenGL 库的开发者自行决定。…...

持续集成工具jenkins操作
安装Jenkins 下载jenkins安装包 linux上下载jenkins失败 开始在windows上安装jenkins 1、先安装JDK https://jingyan.baidu.com/article/fdbd4277dd90f0b89e3f489f.html 免安装版本JDK只需要解压配置环境变量即可 2、安装Jenkins 参考文档: https://www.cnb…...

使用BurpSuite抓取HTTPS接口
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 原因设置方式 原因 BurpSuite之所以不能抓取https数据包,是因为BurpSuite作为中间人代理,我们和https网站之间的数据通信都是由BurpSuite来…...
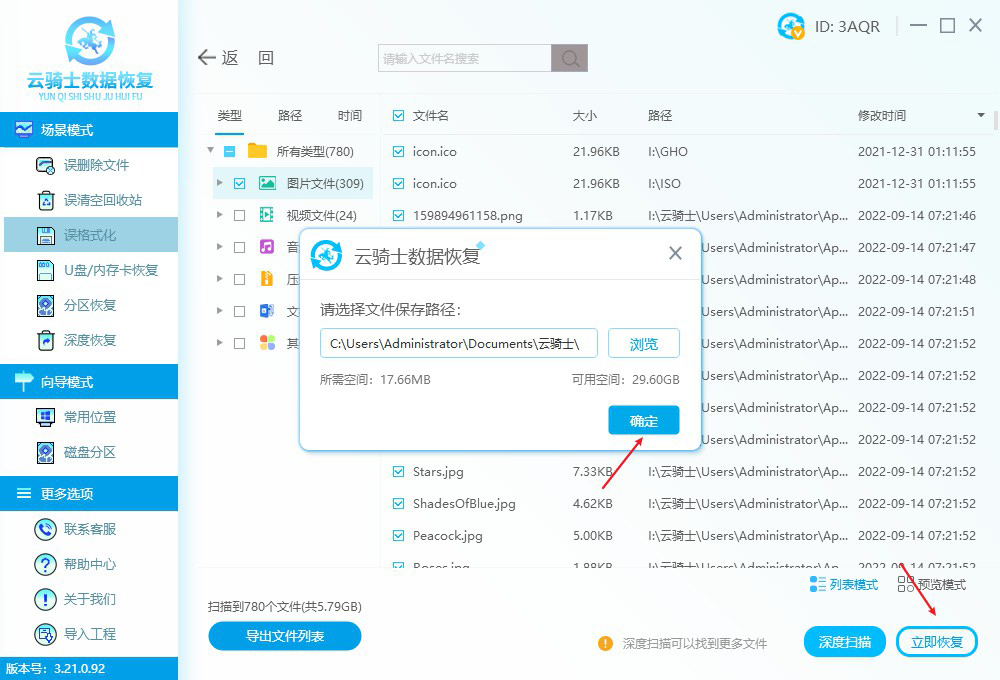
移动硬盘被格式化了如何恢复数据?四步教你如何恢复
在日常生活中,我们常常会使用各种存储设备来保存和备份我们的重要数据。移动硬盘作为一种便携式的存储设备,被广泛应用于数据的存储和传输。然而,有时候我们会不小心将移动硬盘格式化,从而丢失了里面的数据。本文将介绍移动硬盘格…...

基于变电站自动化系统中的安全措施分析及应用
摘要:阐述变电运行中的问题,电气自动化系统与安全运行措施,包括自动控制设备的投入,电气自动 化与计算机技术相、设备数据的采集与处理、自动化系统的升级、人工智能技术的应用。 关键词:自动控制;数据采…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
