卷积神经网络CNN学习笔记
目录
- 1.全连接层存在的问题
- 2.卷积运算
- 3.填充(padding)
- 3.1填充(padding)的意义
- 4.步幅(stride)
- 5.三维数据的卷积运算
- 6.结合方块思考
- 7.批处理
- 8.conv2d代码
- 参考文章
1.全连接层存在的问题
在全连接层中,相邻层的神经元全部连接在一起,输出的数量可以任意决定。全连接层存在什么问题呢?那就是数据的形状被“忽视”了。比如,输入数据是图像时,图像通常是高、长、通道方向上的3维形状。但是,向全连接层输入时,需要将3维数据拉平为1维数据。实际上,前面提到的使用了MNIST数据集的例子中,输入图像就是1通道、高28像素、长28像素的(1, 28, 28)形状,但却被排成1列,以784个数据的形式输入到最开始的Affine层。图像是3维形状,这个形状中应该含有重要的空间信息。比如,空间上邻近的像素为相似的值、RBG的各个通道之间分别有密切的关联性、相距较远的像素之间没有什么关联等,3维形状中可能隐藏有值得提取的本质模式。但是,因为全连接层会忽视形状,将全部的输入数据作为相同的神经元(同一维度的神经元)处理,所以无法利用与形状相关的信息。而卷积层可以保持形状不变。当输入数据是图像时,卷积层会以3维数据的形式接收输入数据,并同样以3维数据的形式输出至下一层。因此,在CNN中,可以(有可能)正确理解图像等具有形状的数据。另外,CNN 中,有时将卷积层的输入输出数据称为特征图(feature map)。其中,卷积层的输入数据称为输入特征图(input feature map),输出数据称为输出特征图(output feature map)。本文中将“输入输出数据”和“特征图”作为含义相同的词使用.
2.卷积运算
卷积层进行的处理就是卷积运算。卷积运算相当于图像处理中的“滤波器运算”。在介绍卷积运算时,我们来看一个具体的例子(图7-3)。

如图7-3所示,卷积运算对输入数据应用滤波器。在这个例子中,输入数据是有高长方向的形状的数据,滤波器也一样,有高长方向上的维度。假设用(height, width)表示数据和滤波器的形状,则在本例中,输入大小是(4, 4),滤波器大小是(3, 3),输出大小是(2, 2)。另外,有的文献中也会用“核”这个词来表示这里所说的“滤波器”。现在来解释一下图7-3的卷积运算的例子中都进行了什么样的计算。图7-4中展示了卷积运算的计算顺序。对于输入数据,卷积运算以一定间隔滑动滤波器的窗口并应用。这里所说的窗口是指图7-4中灰色的3 × 3的部分。如图7-4所示,将各个位置上滤波器的元素和输入的对应元素相乘,然后再求和(有时将这个计算称为乘积累加运算)。然后,将这个结果保存到输出的对应位置。将这个过程在所有位置都进行一遍,就可以得到卷积运算的输出。在全连接的神经网络中,除了权重参数,还存在偏置。CNN中,滤波器的参数就对应之前的权重。并且,CNN中也存在偏置。图7-3的卷积运算的例子一直展示到了应用滤波器的阶段。包含偏置的卷积运算的处理流如图7-5所示。如图7-5所示,向应用了滤波器的数据加上了偏置。偏置通常只有1个(1 × 1)(本例中,相对于应用了滤波器的4个数据,偏置只有1个),这个值会被加到应用了滤波器的所有元素上。


3.填充(padding)
在进行卷积层的处理之前,有时要向输入数据的周围填入固定的数据(比如0等),这称为填充(padding),是卷积运算中经常会用到的处理。比如,在图7-6的例子中,对大小为(4, 4)的输入数据应用了幅度为1的填充。“幅度为1的填充”是指用幅度为1像素的0填充周围。

如图7-6所示,通过填充,大小为(4, 4)的输入数据变成了(6, 6)的形状。然后,应用大小为(3, 3)的滤波器,生成了大小为(4, 4)的输出数据。这个例子中将填充设成了1,不过填充的值也可以设置成2、3等任意的整数。在图7-5的例子中,如果将填充设为2,则输入数据的大小变为(8, 8);如果将填充设为3,则大小变为(10, 10)
3.1填充(padding)的意义
使用填充主要是为了调整输出的大小。比如,对大小为(4, 4)的输入数据应用(3, 3)的滤波器时,输出大小变为(2, 2),相当于输出大小比输入大小缩小了 2个元素。这在反复进行多次卷积运算的深度网络中会成为问题。为什么呢?因为如果每次进行卷积运算都会缩小
空间,那么在某个时刻输出大小就有可能变为 1,导致无法再应用卷积运算。为了避免出现这样的情况,就要使用填充。在刚才的例子中,将填充的幅度设为 1,那么相对于输入大小(4, 4),输出大小也保持为原来的(4, 4)。因此,卷积运算就可以在保持空间大小不变
的情况下将数据传给下一层。
4.步幅(stride)

在图7-7的例子中,对输入大小为(7, 7)的数据,以步幅2应用了滤波器。通过将步幅设为2,输出大小变为(3, 3)。像这样,步幅可以指定应用滤波器的间隔。综上,增大步幅后,输出大小会变小。而增大填充后,输出大小会变大。如果将这样的关系写成算式,会如何呢?接下来,我们看一下对于填充和步幅,如何计算输出大小。这里,假设输入大小为(H, W),滤波器大小为(FH, FW),输出大小为(OH, OW),填充为P,步幅为S。此时,输出大小可通过式(7.1)进行计算。
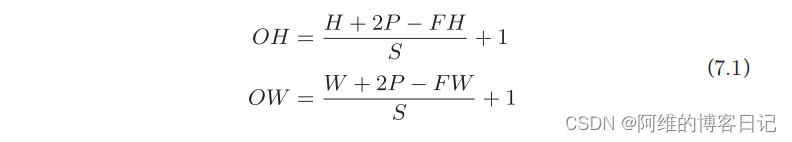

5.三维数据的卷积运算
之前的卷积运算的例子都是以有高、长方向的2维形状为对象的。但是,图像是3维数据,除了高、长方向之外,还需要处理通道方向。这里,我们按照与之前相同的顺序,看一下对加上了通道方向的3维数据进行卷积运算的例子。图7-8是卷积运算的例子,图7-9是计算顺序。这里以3通道的数据为例,展示了卷积运算的结果。和2维数据时(图7-3的例子)相比,可以发现纵深方向(通道方向)上特征图增加了。通道方向上有多个特征图时,会按通道进行输入数据和滤波器的卷积运算,并将结果相加,从而得到输出。


需要注意的是,在3维数据的卷积运算中,输入数据和滤波器的通道数要设为相同的值。在这个例子中,输入数据和滤波器的通道数一致,均为3。滤波器大小可以设定为任意值(不过,每个通道的滤波器大小要全部相同)。这个例子中滤波器大小为(3, 3),但也可以设定为(2, 2)、(1, 1)、(5, 5)等任意值。再强调一下,通道数只能设定为和输入数据的通道数相同的值(本例中为3)。
6.结合方块思考
将数据和滤波器结合长方体的方块来考虑,3维数据的卷积运算会很容易理解。方块是如图7-10所示的3维长方体。把3维数据表示为多维数组时,书写顺序为(channel, height, width)。比如,通道数为C、高度为H、长度为W的数据的形状可以写成(C, H, W)。滤波器也一样,要按(channel, height, width)的顺序书写。比如,通道数为C、滤波器高度为FH(Filter Height)、长度为FW(Filter Width)时,可以写成(C, FH, FW)。

在这个例子中,数据输出是1张特征图。所谓1张特征图,换句话说,就是通道数为1的特征图。那么,如果要在通道方向上也拥有多个卷积运算的输出,该怎么做呢?为此,就需要用到多个滤波器(权重)。用图表示的话,如图7-11所示。

图7-11中,通过应用FN个滤波器,输出特征图也生成了FN个。如果将这FN个特征图汇集在一起,就得到了形状为(FN, OH, OW)的方块。将这个方块传给下一层,就是CNN的处理流。如图 7-11 所示,关于卷积运算的滤波器,也必须考虑滤波器的数量。因此,作为4维数据,滤波器的权重数据要按(output_channel, input_channel, height, width)的顺序书写。比如,通道数为3、大小为5 × 5的滤波器有20个时,可以写成(20, 3, 5, 5)。卷积运算中(和全连接层一样)存在偏置。在图7-11的例子中,如果进一步追加偏置的加法运算处理,则结果如下面的图7-12所示。图7-12中,每个通道只有一个偏置。这里,偏置的形状是(FN, 1, 1),滤波器的输出结果的形状是(FN, OH, OW)。这两个方块相加时,要对滤波
器的输出结果(FN, OH, OW)按通道加上相同的偏置值。另外,不同形状的方块相加时,可以基于NumPy的广播功能轻松实现(1.5.5节)。

7.批处理
神经网络的处理中进行了将输入数据打包的批处理。之前的全连接神经网络的实现也对应了批处理,通过批处理,能够实现处理的高效化和学习时对mini-batch的对应。我们希望卷积运算也同样对应批处理。为此,需要将在各层间传递的数据保存为4维数据。具体地讲,就是按(batch_num, channel, height, width)的顺序保存数据。比如,将图7-12中的处理改成对N个数据进行批处理时,数据的形状如图7-13所示。图7-13的批处理版的数据流中,在各个数据的开头添加了批用的维度。像这样,数据作为4维的形状在各层间传递。这里需要注意的是,网络间传递的是4维数据,对这N个数据进行了卷积运算。也就是说,批处理将N次的处理汇总成了1次进行.

8.conv2d代码
import torch
import torch.nn as nn# 设定一个[1, 3, 5, 5]的输入
input = torch.Tensor([[[[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5]],[[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5]],[[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5]]]])
# 设定一个卷积
conv = nn.Conv2d(in_channels=3,out_channels=3,kernel_size=3,#这里的kernel_size=3和kernel_size=(3,3)意思一样stride=1,padding=0,# 注意,这里padding=0意思是不填充任何数字# 若padding=1,则举个例子,原来的(3,3)是填充为(5,5),而非(4,4)dilation=1,groups=3)# 设定卷积的权重数值
conv.weight.data = torch.Tensor([[[[1, 1, 1],[1, 1, 1],[1, 1, 1]]],[[[2, 2, 2],[2, 2, 2],[2, 2, 2]]],[[[3, 3, 3],[3, 3, 3],[3, 3, 3]]]])
# 利用卷积得到输出
output = conv(input)
print(output)
参考文章
[1]Pytorch的nn.Conv2d详解
相关文章:

卷积神经网络CNN学习笔记
目录 1.全连接层存在的问题2.卷积运算3.填充(padding)3.1填充(padding)的意义 4.步幅(stride)5.三维数据的卷积运算6.结合方块思考7.批处理8.conv2d代码参考文章 1.全连接层存在的问题 在全连接层中,相邻层的神经元全部连接在一起,输出的数量可以任意决…...

Java的Socket Timeout和tcp的存活探测包是不是一个东西
背景 你有没有好奇过我们在java中通过Socket.setSoTimeout()设置timeout参数时,他怎么做到在timeout时间到了之后连接就报错的?有没有产生过误解,这个参数就是设置keepalive探测包的检测间隔? 问题真相 其实Socket.setSoTimeou…...

基于跳蛛优化的BP神经网络(分类应用) - 附代码
基于跳蛛优化的BP神经网络(分类应用) - 附代码 文章目录 基于跳蛛优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.跳蛛优化BP神经网络3.1 BP神经网络参数设置3.2 跳蛛算法应用 4.测试结果:5.M…...

基于鹈鹕优化的BP神经网络(分类应用) - 附代码
基于鹈鹕优化的BP神经网络(分类应用) - 附代码 文章目录 基于鹈鹕优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.鹈鹕优化BP神经网络3.1 BP神经网络参数设置3.2 鹈鹕算法应用 4.测试结果:5.M…...
『ARM』和『x86』处理器架构解析指南
前言 如果问大家是否知道 CPU,我相信不会得到否定的答案,但是如果继续问大家是否了解 ARM 和 X86 架构,他们的区别又是什么,相信可能部分人就会哑口无言了 目前随着深度学习、高性能计算、NLP、AIGC、GLM、AGI 的技术迭代&#…...

Android 13.0 系统设置 app详情页默认关闭流量数据的开关
1.概述 在13.0的系统产品开发中,移动流量消耗也是关于产品优化的一个方面,由于产品需求需要对app详情页的流量进行管控默认关闭流量开关,不让流量无故流失,所以需要从流量开关分析问题流量打开流程,然后关闭 2.系统设置 app详情页默认关闭流量数据的开关的核心类 package…...
054协同过滤算法的电影推荐系统
大家好✌!我是CZ淡陌。一名专注以理论为基础实战为主的技术博主,将再这里为大家分享优质的实战项目,本人在Java毕业设计领域有多年的经验,陆续会更新更多优质的Java实战项目,希望你能有所收获,少走一些弯路…...

分享一个基于JavaWeb的私人牙科诊所预约挂号就诊系统的设计与实现项目源码调试 lw 开题 ppt
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等,大家有这一块的问题可以一起交流! 💕&…...
)
从零开始的C++(十一)
vector的模拟实现: 1.构造函数: vector(){}vector(int n, const T& value T()){ reserve(n);for (int i 0; i < n; i){push_back(value);}}template<class InputIterator>vector(InputIterator first, InputIterator last){ auto it …...

驱动开发day2
通过物理内存映射为虚拟内存 实现三盏LED灯亮灯灭 head.h #ifndef __HEAD_H__ #define __HEAD_H__#define PHY_LED1_MODER 0X50006000 #define PHY_LED1_ODR 0X50006014 #define PHY_RCC 0x50000A28#define PHY_LED2_MODER 0X50007000 #define PHY_LED2_ODR 0X50007014#defin…...
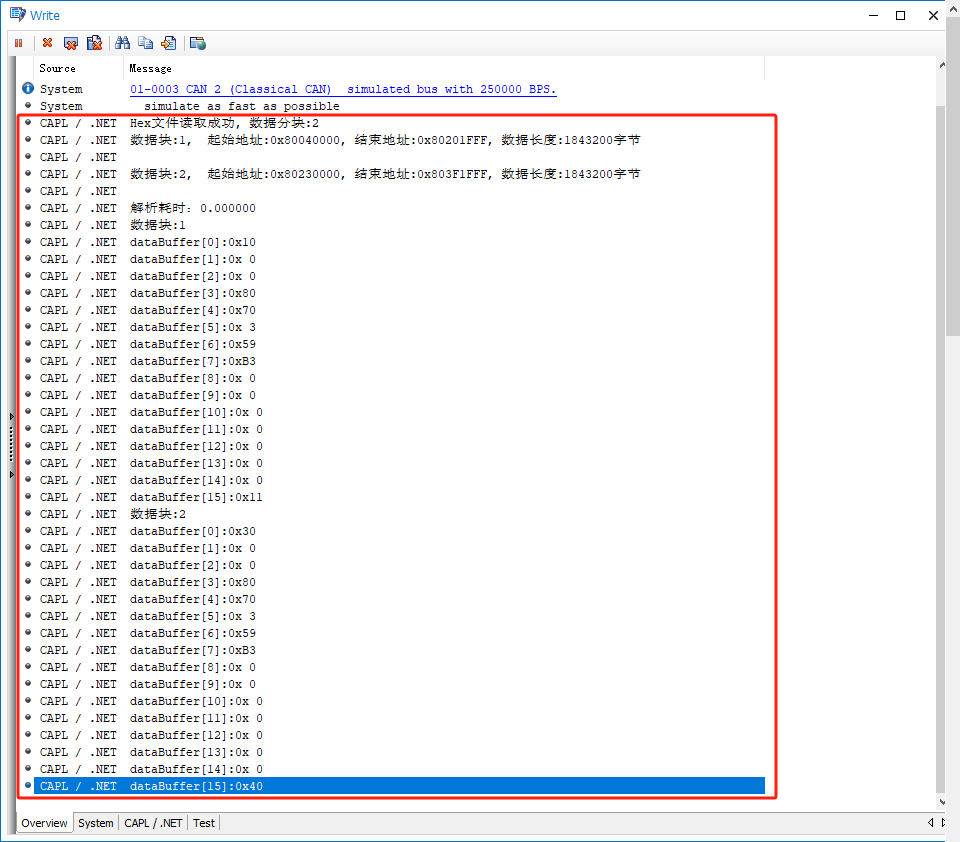
【CANoe】文件处理_hex文件读取解析
hex文件里面只有00,01,04三种码。那么我们在解析的时候只需要对这三种不同状态的进行不同的解析即可。 hex文件格式的解析,可阅读:HEX文件格式详解 首先创建一个Block的结构体,根据经验我们知道,一个数据…...

人脸识别顶会论文及源码合集,含2023最新
今天和大家聊聊人脸识别。 人脸识别的技术经过不断发展已经相当成熟,在门禁、监控、手机解锁、移动支付等实际场景都能看到。我们比较熟悉的识别方式是基于可见光图像的人脸识别,这种方式有个非常明显的缺点:光线限制。 在近两年的人脸识别…...

介绍drawio和图表使用场景
图表介绍 drawio是一个基于Web技术的草图、简图和图表的解决方案。 drawio支持在线编辑器,app.diagram.net.并支持不同的操作系统的桌面版离线安装版本。如:windows, linux, macOS。 对于个人或者团队,把图表绘制的安全放到第一位ÿ…...

leetcode-1438: 绝对差不超过限制的最长连续子数组
给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。 如果不存在满足条件的子数组,则返回 0 。 示例 1: 输入&#x…...

【数据结构初阶】九、排序的讲解和实现(直接插入 \ 希尔 \ 直接选择 \ 堆 \ 冒泡 -- C语言)
相关代码gitee自取: C语言学习日记: 加油努力 (gitee.com) 接上期: 【数据结构初阶】八、非线性表里的二叉树(二叉树的实现 -- C语言链式结构)-CSDN博客 排序 排序的概念 所谓排序,就是使一串记录,按照…...
uview组件使用笔记
图标样式 修改图标的样式 通过color参数修改图标的颜色通过size参数修改图标的大小,单位为rpx 效果图 <u-icon name"photo" color"#2979ff" size"28"></u-icon>图片图标 1.3.0 这里说的图片图标,指的是小…...
Linux1024一篇通俗易懂的liunx命令操作总结(第十课)
Linux1024一篇通俗易懂的liunx命令操作总结(第十课) 一 liunx 介绍 Linux是一种免费开源的操作系统,它的设计基于Unix。它最早是由芬兰的一位大学生Linus Torvalds在1991年开始编写的,取名为Linux。Linux具有高度的灵活性和可定制性,可以在…...
nuxt使用i18n进行中英文切换
中文效果图: 英文效果图: 版本: 安装: npm install --save nuxtjs/i18n 新建en.js与zh.js两个文件进行切换显示 en.js内容 import globals from ./../js/global_valexport default {/******* 公共内容开始* *****/seeMore: &quo…...

机器人制作开源方案 | 行星探测车实现WiFi视频遥控功能
1. 功能描述 本文示例所实现的功能为:用手机APP,通过WiFi通信遥控R261样机行星探测车移动,以及打开、关闭行星探测车太阳翼。 2. 电子硬件 在这个示例中,我们采用了以下硬件,请大家参考: 主控板 Basra主控…...

Angular main 中的enableProdMode
enableProdMode一次深度解析 在Angular的开发过程中,我们经常会遇到一个名为enableProdMode的设置。这个设置位于Angular的主模块(main module)中,它的主要作用是启用生产模式。那么,什么是生产模式?为什么…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...
