机器学习终极指南:统计和统计建模03/3 — 第 -3 部分
系列上文:机器学习终极指南:特征工程(02/2) — 第 -2 部分
一、说明
在终极机器学习指南的第三部分中,我们将了解统计建模的基础知识以及如何在 Python 中实现它们,Python 是一种广泛用于数据分析和科学计算的强大编程语言。我们将介绍概率分布、假设检验、回归分析和分类等基本概念,以及数据准备、模型选择和评估等动手技术。

图例.1 — 统计和统计建模
在许多领域,包括数据科学、机器学习和金融,统计建模是理解和分析数据的基本工具。我们可以通过开发捕获变量之间关系的数学模型来做出预测、测试假设并深入了解复杂现象。
本指南将为您提供解决实际数据问题和做出数据驱动型决策所需的知识和工具。那么,让我们开始使用Python,探索令人兴奋的统计建模世界。
二、内容提要
- 概率论
- 描述统计学
- 推论统计
- 广义线性模型
- 贝叶斯统计与推理
- 马尔可夫链蒙特卡洛 (MCMC)
- 结论
三、概率论概念
概率论是研究随机事件的数学分支。它提供了一个框架,用于理解事件发生的可能性以及我们如何根据这些概率进行预测。

图例.2 - 概率论
我们从概率论中的样本空间开始,它是实验所有可能结果的集合。之后,我们将事件定义为样本空间的子集,并为它们分配概率。事件的概率是介于 0 和 1 之间的数字,0 表示不可能,1 表示确定。考虑一个公平的六面骰子的滚动。在这种情况下,随机变量是从掷骰子中获得的数字。该随机变量的概率分布由均匀分布给出,其中随机变量的每个值都有相等的发生机会。
3.1 期望值和方差
期望值和方差的概念在概率论中是必不可少的。随机变量的期望值是多次重复实验所需的平均值。方差是随机变量偏离其期望值的量。
考虑计算正态分布、均值为 0、标准差为 1 的随机变量的期望值和方差。要从正态分布生成随机数,我们可以使用 NumPy 库:
import numpy as np# Generate 10000 random numbers from a normal distribution
rand_nums = np.random.normal(loc=0, scale=1, size=10000)# Calculate the expected value and variance
expected_value = np.mean(rand_nums)
variance = np.var(rand_nums)print(f"Expected value: {expected_value:.2f}")
print(f"Variance: {variance:.2f}")在概率论中,条件概率和贝叶斯定理也是重要的概念。给定一个事件发生的另一个事件的概率称为条件概率。贝叶斯定理是一个公式,用于描述如何根据新信息更新事件的概率。
例如,考虑一项医学测试,当疾病存在时,检测疾病的准确率为 95%,但假阳性率为 5%。如果该疾病在人群中的患病率为1%,那么检测呈阳性的人实际上患有该疾病的概率是多少?
# Define the probabilities
p_disease = 0.01
p_no_disease = 1 - p_disease
p_positive_given_disease = 0.95
p_positive_given_no_disease = 0.05# Calculate the probability of testing positive
p_positive = (p_positive_given_disease * p_disease) + (p_positive_given_no_disease * p_no_disease)# Calculate the probability of having the disease given a positive test
p_disease_given_positive = (p_positive_given_disease * p_disease) / p_positiveprint(f"Probability of having the disease given a positive test: {p_disease_given_positive:.2f}")3.2 概率分布
概率分布是描述随机事件中不同结果的概率的数学函数。概率分布有多种类型,每种类型都有自己的一组特征和应用。一些最常见的概率分布及其属性如下:
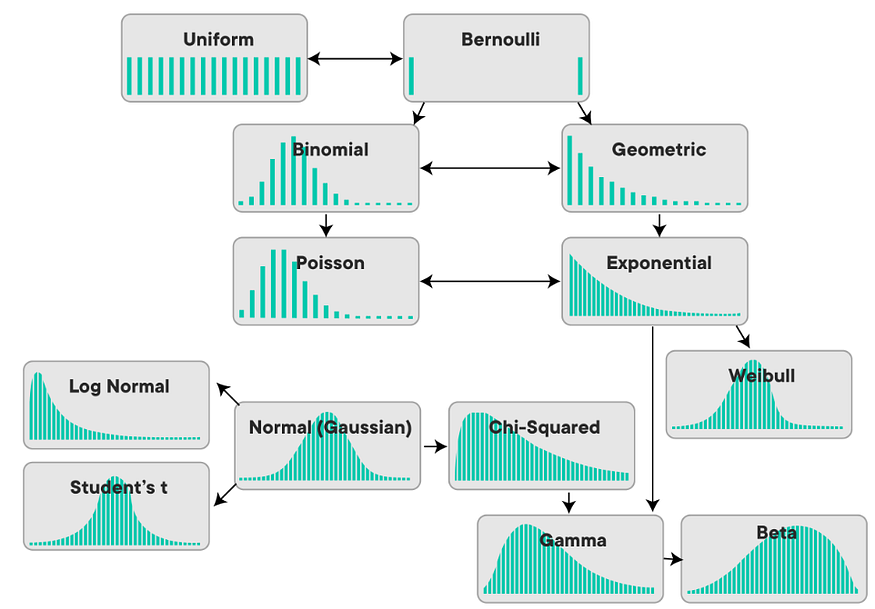
图例.3 — 概率分布
a. 正态分布: 它是具有钟形曲线的连续分布,也称为高斯分布。它通常用于统计中描述现实世界的现象,例如智商分数、身高和体重。分布的均值 (μ) 和标准差 (σ) 是两个参数。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm# Create a normal distribution with mean 0 and standard deviation 1
mu, sigma = 0, 1
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
plt.plot(x, norm.pdf(x, mu, sigma))
plt.show()b. 二项分布:它是一个离散分布,描述了在给定数量的试验中给定数量的成功的可能性。它有两个参数:n(试验次数)和p(成功概率)(每次试验成功的概率)。
from scipy.stats import binom# Create a binomial distribution with n=10 and p=0.5
n, p = 10, 0.5
x = np.arange(binom.ppf(0.01, n, p), binom.ppf(0.99, n, p))
plt.plot(x, binom.pmf(x, n, p), 'bo', ms=8)
plt.show()c. 泊松分布:它是一个离散分布,描述在给定的时间或空间间隔内发生一定数量事件的可能性。它只有一个参数 λ(每个间隔的平均事件数)。
from scipy.stats import poisson# Create a Poisson distribution with lambda=2
mu = 2
x = np.arange(poisson.ppf(0.01, mu), poisson.ppf(0.99, mu))
plt.plot(x, poisson.pmf(x, mu), 'bo', ms=8)
plt.show()d. 指数分布:它是一个连续分布,描述了泊松过程中事件之间的时间,其中事件随机且独立地发生。它只有一个参数λ(泊松过程的速率)。
from scipy.stats import expon# Create an exponential distribution with lambda=0.5
rate = 0.5
x = np.linspace(0, 10, 100)
plt.plot(x, expon.pdf(x, scale=1/rate))
plt.show()e. 伽马分布: 它是一个连续分布,描述了泊松过程中 k 个事件之间的时间,其中每个事件的速率为 λ。它有两个参数,k 和 λ。
from scipy.stats import gamma# Create a gamma distribution with k=2 and lambda=0.5
k, theta = 2, 1/0.5
x = np.linspace(gamma.ppf(0.01, k), gamma.ppf(0.99, k), 100)
plt.plot(x, gamma.pdf(x, k, scale=theta))
plt.show()概率论是一个棘手的话题,但它对于理解和分析随机事件及其结果是必要的。通过使用Python和数学,我们可以更好地理解这些概念并将其应用于现实世界的问题。
四、描述统计学
描述性统计可用于通过创建数据样本摘要来描述数据集的特征。人口普查可能包括描述性信息,例如特定城市的男性和女性比例。

图例.4 — 描述性统计
4.1 集中趋势和变异性的度量
这些是用于描述数据集特征的统计概念。
中心趋势:最能代表整个数据集的值是中心趋势。它可以使用多种方法进行计算,包括平均值、中位数和众数。
- 意味 着:它的计算方法是将数据点总数除以数据点总数。它是最常用的集中趋势度量。平均值可以使用以下公式计算:平均值 = (所有值的总和) / (值的数量) 我们可以使用 NumPy 库计算 Python 中数据集的平均值,如下所示:
import numpy as np
data = np.array([2, 4, 6, 8, 10])
mean = np.mean(data)
print("Mean:", mean)- 中位数: 它是数据集的中间值。它是将排序数据集中上 50% 的数据与下部 50% 的数据分开的值。如果数据集中有偶数个值,则中位数是两个中间值的平均值。我们可以使用 NumPy 库计算 Python 中数据集的中位数,如下所示:
import numpy as np
data = np.array([2, 4, 6, 8, 10])
median = np.median(data)
print("Median:", median)- 模式: 它是数据集中出现频率最高的值。数据集中可以有一个或多个模式。我们可以使用 SciPy 库计算 Python 中数据集的模式,如下所示:
import scipy.stats as stats
data = [2, 4, 6, 8, 10, 10]
mode = stats.mode(data)
print("Mode:", mode)变异性:数据点围绕集中趋势的扩散或分散是通过可变性来衡量的。变异性通常使用范围、方差和标准差来衡量。
- 范围:它是数据集的最大值和最小值之间的差异。我们可以使用 NumPy 库计算 Python 中数据集的范围,如下所示:
import numpy as np
data = np.array([2, 4, 6, 8, 10])
range = np.max(data) - np.min(data)
print("Range:", range)- 方差: 它是与平均值的平方偏差之和。它确定数据与平均值的偏差程度。方差使用以下公式计算:方差 = sum((xi — mean)2) / (n — 1) 我们可以使用 NumPy 库计算 Python 中数据集的方差,如下所示:
import numpy as np
data = np.array([2, 4, 6, 8, 10])
variance = np.var(data, ddof=1)
print("Variance:", variance)- 标准差:它是方差的平方根。它用于计算数据集中数据的分布。可以使用以下公式计算标准偏差: sqrt = 标准差(方差) 数据集的标准差可以在 Python 中使用 NumPy 库计算,如下所示:
import numpy as np
data = np.array([2, 4, 6, 8, 10])
std_dev = np.std(data, ddof=1)
print("Standard Deviation:", std_dev)For Histograms and Visualisation plots, and Correlation and covariance Checkout — EDA — Part1 and for Skewness and kurtosis Checkout — Feature Engineering Part -2
4.2 推论统计
推论统计是一种利用样本数据得出有关较大总体的结论的统计数据。通过分析总体数据样本,推论统计可以对该总体进行预测并得出结论。
为了做出这些推论,推论统计采用基于概率论的假设检验和置信区间等技术。
Fig.5- Inferential Statistics
- Hypothesis Testing
假设检验是一种统计方法,用于确定数据是否支持有关总体参数的假设。它包括确定零假设(表示两组之间不存在差异的假设)和备择假设(表示两组之间存在差异的主张)。
假设检验涉及的基本步骤是:
- 陈述原假设和备择假设
- 选择显著性水平 (alpha)
- 收集数据并计算检验统计量
- 确定 p 值
- 根据 p 值和显著性水平得出结论
下面是假设检验的示例:
假设一家公司声称他们的新产品将使销售额增加至少 10%。为了检验这一说法,我们可以将原假设设置为:
H0:由于新产品(μ ≤0)没有增加销售额
替代假设为:
Ha:由于新产品(μ >0)的销售额增加
之后,我们可以收集新产品发布前后的销售数据,并计算检验统计量(例如,t统计量)。然后,我们可以使用此检验统计量计算 p 值,该统计量表示假设原假设为真,获得与观察到的检验统计量一样极端的概率。
如果 p 值小于所选显著性水平 (alpha),则否定原假设并找到备择假设的证据。如果 p 值大于 alpha,则我们无法否定原假设,并得出结论,备择假设的证据不足。
在 Python 中,我们可以使用 scipy.stats 模块来执行假设检验。下面是一个 t 检验的示例:
import numpy as np
from scipy.stats import ttest_ind# Generate some sample data
group1 = np.random.normal(10, 2, size=50)
group2 = np.random.normal(12, 2, size=50)# Perform a two-sample t-test
t, p = ttest_ind(group1, group2)print("t-statistic:", t)
print("p-value:", p)2. 置信区间
推论统计使用置信区间来估计总体参数,例如基于数据样本的平均值或比例。置信区间是具有一定确定性的值范围,其中包含参数的真实值。
假设我们要估计学校中所有学生的平均身高。我们可以测量随机抽样学生的身高,并使用样本均值来估计总体均值。但是,我们不知道这个估计有多精确。通过构建置信区间,我们可以提供一个值范围,这些值可能包含具有一定置信度的真实总体均值。
图片-------------------------------------------------------
图例.6 — 置信区间
要创建置信区间,我们必须首先选择一个置信水平,通常为 90%、95% 或 99%。置信水平表示如果采样过程重复多次,区间包含真实总体参数的次数比例。例如,95% 置信区间意味着,如果我们取 100 个样本并为每个样本构建一个置信区间,其中大约 95 个区间将包含真实的总体参数。
置信区间的公式由样本数量和样本数据的分布确定。例如,如果样本数量很大且数据呈正态分布,我们可以使用以下公式来计算总体均值的 95% 置信区间:
置信区间 = x̄ ± 1.96 * (s / √n)
其中 CI 是置信区间,x̄ 是样本均值,s 是样本标准差,n 是样本数量,1.96 是 95% 置信水平的 z 得分。
在 Python 中,我们可以使用 scipy.stats 模块来计算置信区间。例如,要从数据样本中计算总体均值的 95% 置信区间,我们可以使用以下代码:
import numpy as np
from scipy.stats import t# Generate some sample data
data = np.random.normal(0, 1, size=100)# Calculate the sample mean and standard deviation
xbar = np.mean(data)
s = np.std(data, ddof=1)# Calculate the t-value for a 95% confidence level with n-1 degrees of freedom
tval = t.ppf(0.975, len(data)-1)# Calculate the confidence interval
ci = (xbar - tval*s/np.sqrt(len(data)), xbar + tval*s/np.sqrt(len(data)))print(ci)3. 功率分析
功效分析是一种统计方法,用于确定研究所需的样本量,以检测显著效应(如果存在)。研究的功效是检测到显着效应的可能性,假设存在。功效分析对于确定研究所需的样本量非常有用,以避免II类错误(假阴性)并确保研究结果可靠有效。

图片.7 — 功率分析
进行功效分析时必须考虑几个因素,包括所需的显著性水平 (alpha)、效应大小和样本数量。两个变量之间的差异大小或关系称为效应大小,通常表示为差异的标准化度量,例如科恩的d。功效分析还考虑样本数量,因为较大的样本数量通常会导致更高的功效。
下面是使用statsmodels该库在 Python 中进行功耗分析的示例:
import statsmodels.stats.power as smp# Set parameters for power analysis
effect_size = 0.5
alpha = 0.05
power = 0.8# Conduct power analysis
nobs = smp.tt_ind_solve_power(effect_size=effect_size, alpha=alpha, power=power)print("Sample size: ", round(nobs))在此示例中,我们将效应大小设置为 0.5,这被视为中等效应大小,将 alpha 水平设置为 0.05(这是常用的显著性水平),将功率水平设置为 0.8,这是常用的功效水平。然后使用 tt ind 求解幂函数计算具有指定参数的双样本 t 检验所需的样本数量。代码返回所需的样本大小,四舍五入到最接近的整数。
五、广义线性模型
GLM 是一种统计模型,它扩展了线性回归模型以处理非正态和非连续响应变量。GLM 背后的基本思想是使用链接函数和概率分布函数来模拟响应变量和预测变量之间的关系。
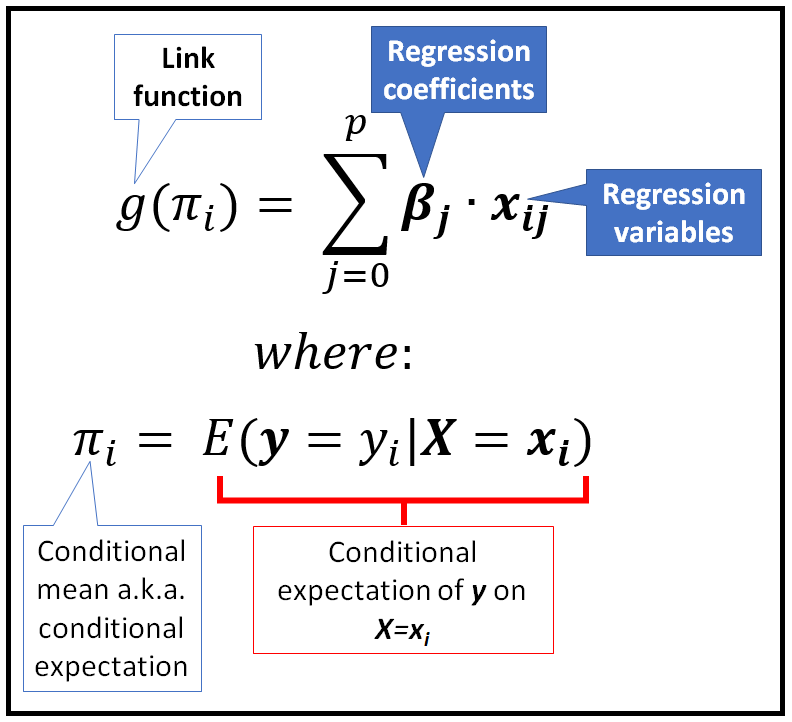
图例.8 — 回归的 GLM 模型(示例)
GLM 的三个关键组成部分是:
- 随机分量: 这描述了响应变量的概率分布。GLM 中最常用的概率分布是正态分布、二项分布和泊松分布。
- 系统组件: 这描述了响应变量和预测变量之间的关系。它是通过预测变量和链接函数的线性组合建模的。
- 链接功能: 这是一个将响应变量的均值与系统分量中的线性预测变量相关联的函数。它是根据响应变量的性质和所使用的分布来选择的。
GLM 及其相关概率分布的一些示例包括:
- 线性回归:正态分布
- 逻辑回归: 二项分布
- 泊松回归: 泊松分布
拟合 GLM 的过程包括指定随机分量、选择适当的链接函数以及使用最大似然估计估计参数。
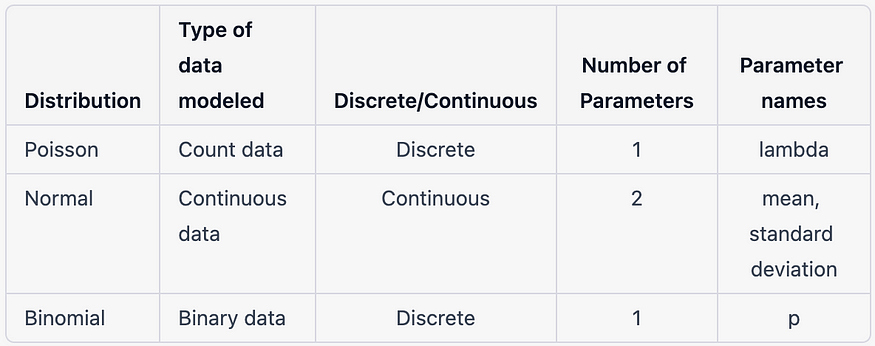
GLM 分布之间的差异
Python有几个用于拟合GLM的软件包,包括statsmodels和scikit-learn。下面是使用统计模型拟合逻辑回归模型的示例:
import statsmodels.api as sm# Load data
data = sm.datasets.get_rdataset("Titanic", "vcd").data# Fit logistic regression model
model = sm.formula.glm("survived ~ age + sex", data=data, family=sm.families.Binomial()).fit()# Print model summary
print(model.summary())响应变量是二元的(存活或未存活),因此使用二项分布。链接函数是逻辑函数,它是二项分布的默认值。model.summary() 函数的输出提供有关每个预测变量的估计系数、标准误差和显著性检验的信息。
让我解释一个使用 GLM 的回归问题,让我们看看泊松回归:
泊松回归是用于对计数数据进行建模的广义线性模型 (GLM) 类型。当响应变量是计数时,它特别有用,例如事件在给定时间段内发生的次数。泊松回归假定响应变量的泊松分布,并将响应变量的期望值建模为预测变量的线性函数。
泊松分布是一种概率分布,它描述了给定平均发生率的给定时间间隔内事件发生的次数。它由称为 lambda 的单个参数定义,该参数表示每单位时间的平均事件数。泊松概率质量函数给出了在给定时间间隔内观测 k 个事件的概率:
P(k) = (lambda^k * e^(-lambda)) / k!
在泊松回归中,假设响应变量 y 服从具有 lambda 平均值的泊松分布,其中 lambda 建模为预测变量的线性函数:
E(y) = lambda = exp(b0 + b1x1 + b2x2 + ... + bpxp)
其中 b0 是截距,b1、b2、...、bp 是回归系数,x1、x2、...、xp 是预测变量。
泊松回归的一个重要假设是响应变量的方差等于其平均值。这称为等离散假设。如果数据违反此假设,则负二项式回归模型可能更合适。
import statsmodels.api as sm
import pandas as pd# Load data
data = pd.read_csv("data.csv")# Fit Poisson regression model
model = sm.GLM(data["y"], data[["x1", "x2", "x3"]], family=sm.families.Poisson()).fit()# Print model summary
print(model.summary())六、贝叶斯统计和我推断
贝叶斯统计是一个统计分支,处理更新信念或概率以响应新证据。它允许将先验知识或信念纳入统计推断和决策。
贝叶斯统计采用贝叶斯定理,这是一个描述两个事件条件概率之间关系的数学公式。根据贝叶斯定理,给定一些观测数据(D)的假设(H)的概率与给定假设的数据乘以假设的先验概率的可能性成正比。
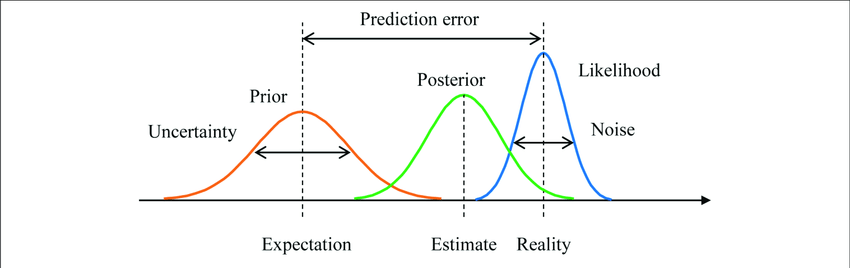
图例.9 — 贝叶斯统计
贝叶斯统计采用贝叶斯定理,这是一个描述两个事件条件概率之间关系的数学公式。根据贝叶斯定理,给定一些观测数据(D)的假设(H)的概率与给定假设的数据乘以假设的先验概率的可能性成正比。
P(H|D) = P(D|H) * P(H) / P(D)
这里:
- P(H|D) 是给定数据 D 的假设 H 的后验概率
- P(D|H) 是给定假设 H 的数据 D 的可能性
- P(H) 是假设 H 的先验概率
- P(D) 是数据 D 的边际概率
import pandas as pd
import statsmodels.api as sm# Load the iris dataset
iris = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',names=['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'species'])# Fit a mixed-effects linear regression model
random = {'sepal_width': '1 + petal_width', 'petal_length': '1 + petal_width*sepal_length'}
model = sm.MixedLM.from_formula('sepal_length ~ petal_length + C(species)', data=iris, re_formula='1', vc_formula=random,groups='species')# Print the summary of the model
result = model.fit()
result.summary()与传统的频率统计相比,贝叶斯统计有几个优点,包括能够整合先验知识,直接估计假设的概率,并在新数据可用时更新信念。贝叶斯统计有许多应用,包括医学研究、社会科学、金融和工程。一个例子是用于药物开发的贝叶斯推理,它使用临床试验的先验知识和数据来估计新药有效的可能性。
贝叶斯推理是一种统计方法,用于根据新证据或数据更新假设或模型的概率。它以数学家托马斯·贝叶斯的名字命名,涉及贝叶斯定理的应用,该定理涉及事件的条件概率。
先验概率分布表示贝叶斯推理中关于假设或模型的先验知识或信念。使用贝叶斯定理,根据观测数据将该先验分布转换为后验分布。给定观测数据,后验分布表示假设或模型的更新概率。
七、马尔可夫链蒙特卡洛 (MCMC)
马尔可夫链蒙特卡罗 (MCMC) 方法是一种用于从复杂概率分布中采样的算法。它们广泛用于贝叶斯推理中,以估计模型参数后验分布。在这个答案中,我们将介绍MCMC方法并提供一个示例Python代码实现。
为了从难以直接采样的复杂分布中生成样本序列,使用了MCMC方法。MCMC方法背后的基本思想是构建一个马尔可夫链,其平稳分布是我们想要从中采样的目标分布。我们可以通过模拟这个马尔可夫链足够长的时间,从目标分布中生成一系列样本。
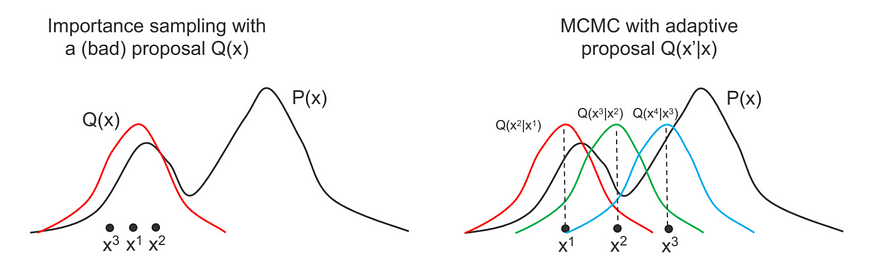
图10 - 马尔可夫链蒙特卡洛(MCMC)
马尔可夫链是随机变量 X1、X2、...、Xn 的序列,其中每个 Xi 都来自仅取决于先前状态 X{i-1} 的概率分布。从一个状态过渡到另一个状态的概率由转换核 K(x{i-1}, xi) 给出。如果以下详细平衡条件成立,则称马尔可夫链是可逆的:
![]()
马尔可夫链
其中 pi(x) 是马尔可夫链的平稳分布。这意味着从 x{i-1} 过渡到 xi 的概率与从 xi 过渡到 x{i-1} 的概率相同。
大都会-黑斯廷斯算法是一种流行的 MCMC 算法,用于从复分布中采样。该算法的工作原理是基于当前状态 x 提出一个新状态 y,并根据接受概率接受或拒绝提议的状态:
![]()
大都会-黑斯廷斯算法
其中 pi(x) 是我们想要采样的目标分布,q(x|y) 是从 y 过渡到 x 的建议分布,q(y|x) 是从 x 过渡到 y 的建议分布。
如果建议的状态 y 被接受,则 x 将更新为 y。如果建议的状态被拒绝,则 x 保持不变。接受概率保证满足详细平衡条件,得到的马尔可夫链以 pi(x) 作为其平稳分布
下面是一个 Metropolis-Hastings 算法的 Python 实现示例,用于从正态分布中采样:
import numpy as np
import matplotlib.pyplot as plt# Define the target distribution
def target(x):return np.exp(-0.5*(x-2)**2) + np.exp(-0.5*(x+2)**2)# Define the proposal distribution
def proposal(x, sigma=1):return np.random.normal(x, sigma)# Initialize the Markov chain
x = 0
samples = []# Run the algorithm
for i in range(10000):# Propose a new statey = proposal(x)# Compute the acceptance probabilityalpha = min(1, target(y)/target(x))# Accept or reject the proposed stateif np.random.rand() < alpha:x = y# Add the sample to the list of samplessamples.append(x)# Plot the samples
plt.hist(samples, bins=50, density=True, label='Estimated distribution')
plt.legend()
plt.show()绘制样本的直方图后,下一步是估计感兴趣参数的后验分布。有不同的方法可以执行此估计,例如核密度估计、高斯混合模型,或者简单地将参数分布(例如,高斯分布)拟合到样本中。
下面是如何使用核密度估计估计后验分布的示例:
from scipy.stats import gaussian_kde# Estimate the posterior distribution using kernel density estimation
kde = gaussian_kde(samples)# Define the range of the x-axis for the plot
x_min = min(samples)
x_max = max(samples)
x_range = np.linspace(x_min, x_max, 1000)# Plot the posterior distribution
plt.plot(x_range, kde(x_range), label='Posterior distribution')
plt.legend()
plt.show() 估计后验分布后,我们可以使用它来计算感兴趣的不同统计量,例如平均值、标准差或分位数。例如,要计算参数的 95% 可信区间,我们可以使用 numpy 中的函数,如下所示:percentile
# Compute the 95% credible interval
lower_bound = np.percentile(samples, 2.5)
upper_bound = np.percentile(samples, 97.5)
print(f"95% credible interval: [{lower_bound}, {upper_bound}]")还有不同的诊断可用于评估 MCMC 算法的性能并检查收敛性。一些常见的诊断包括迹线图、自相关图和格尔曼-鲁宾统计量。这些诊断超出了本答案的范围,但您可以在文献中找到有关它们的更多信息。
八、结论
最终,统计学是一个重要的研究领域,它为理解和分析数据提供了一个框架。统计推断的基础是概率论,它涉及根据样本对总体进行推断。
- 推论统计用于进行预测和测试假设,而描述性统计用于汇总和描述数据。
- 广义线性模型 (GLM) 广泛用于经济学、生物学和流行病学等领域,因为它们为对各种数据类型进行建模提供了灵活的框架。
- 贝叶斯统计和推理为传统的频率主义方法提供了一种强大的替代方案,允许进行更细致和现实的不确定性建模。
- 马尔可夫链蒙特卡罗(MCMC)等方法为模拟复杂概率分布提供了强大的工具,可用于估计
西姆兰吉特·辛格
相关文章:
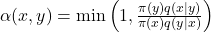
机器学习终极指南:统计和统计建模03/3 — 第 -3 部分
系列上文:机器学习终极指南:特征工程(02/2) — 第 -2 部分 一、说明 在终极机器学习指南的第三部分中,我们将了解统计建模的基础知识以及如何在 Python 中实现它们,Python 是一种广泛用于数据分析和科学计…...

php获取农历日期节日
代码地址:php获取农历日期节日-遇见你与你分享 <?php $c new DayService(); $today$c->convertSolarToLunar(date(Y),date(m),date(d)); $time "农历".$today[1].$today[2]."日";class DayService {var $MIN_YEAR 1891;var $MAX_YEAR …...

主机重启后k8s kubelet无法自动启动问题解决梳理
1.问题描述 OS Version:CentOS Linux release 7.9.2009 (Core) K8S Version:Kubernetes v1.20.4 K8S安装配置完成后,重启服务器发现,kubelet没有正常启动(systemctl status kubelet) 命令: systemctl status kubelet [root@centos79-3 ~]# systemctl status kubelet ●…...
)
Hadoop面试题(2)
1.什么是数据倾斜?如何处理数据倾斜? 数据倾斜指的是在分布式计算中,数据在某些节点上不均匀地分布,导致某些节点的负载过重,影响整体计算性能。 处理数据倾斜的方法主要包括以下几种: 增加分区数量&…...
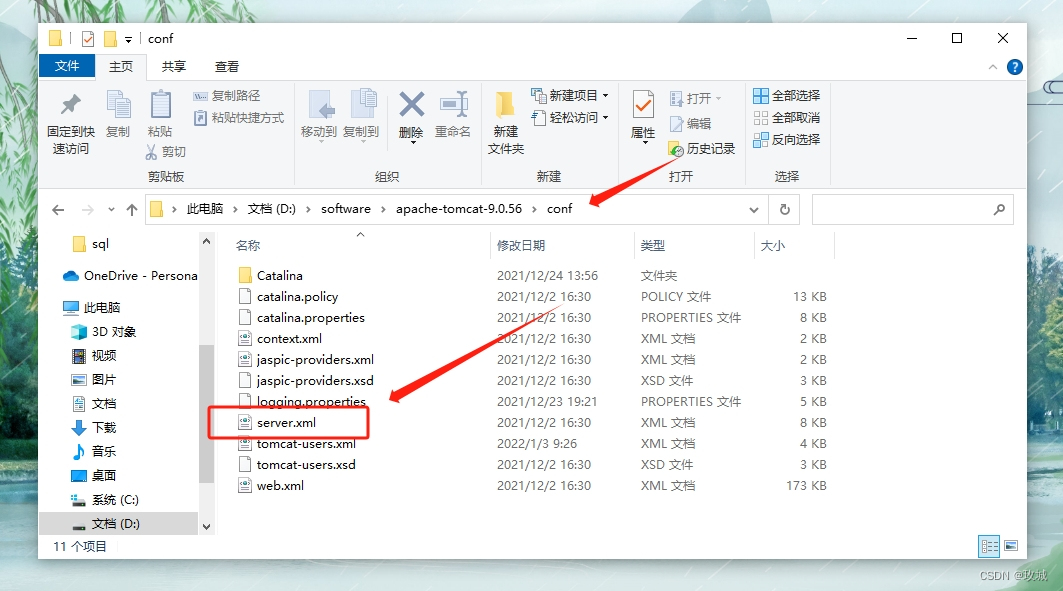
[ Windows-Nginx ]Windows服务器,Tomcat容器部署项目,整合Nginx
一、官网下载Nginx http://nginx.org/en/download.html 稳定版:windows的stable版本 注意:Nginx安装包不要放在中文目录下 二、conf目录下,修改nginx.conf文件 修改Nginx服务端口: 默认端口为80,即外界访问的入口…...
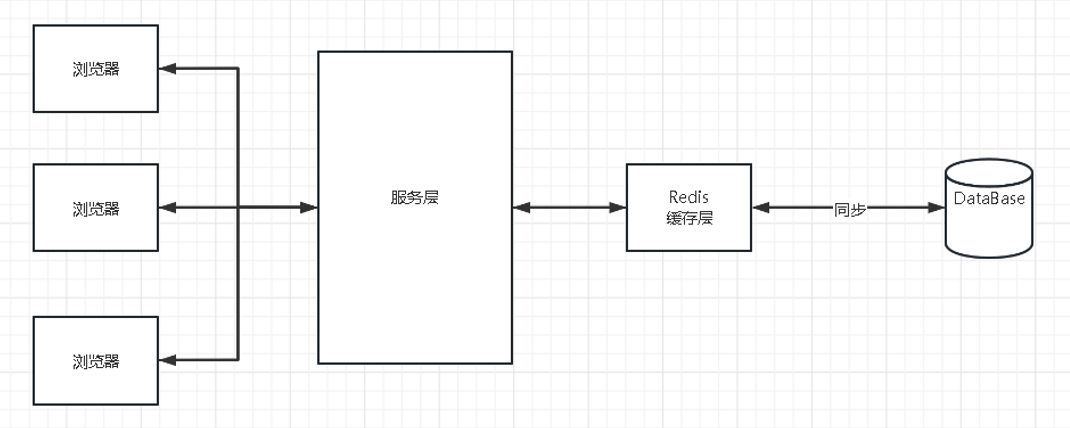
手搭手zabbix5.0监控redis7
Centos7安装配置Redis7 安装redis #安装gcc yum -y install gcc gcc-c #安装net-tools yum -y install net-tools #官网https://redis.io/ cd /opt/ wget http://download.redis.io/releases/redis-7.0.4.tar.gz 解压至/opt/目录下 tar -zxvf redis-7.0.4.tar.gz -C /opt/ #…...

学习笔记02-iview组件使用
学习笔记02-iview组件使用 文章目录 学习笔记02-iview组件使用一、iview 2-Tabs使用 一、iview 2-Tabs使用 官方地址:https://www.iviewui.com/view-ui-plus/component/navigation/tabs 点击tabs页面可以获取当前页面的name信息,并且可以点击后再获取当…...
【java】A卷+B卷)
华为OD 玩牌高手(100分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...

什么是AJAX
AJAX(Asynchronous JavaScript and XML)是一种用于创建交互式、动态网页应用程序的Web开发技术。它允许网页在不刷新整个页面的情况下,与服务器进行异步通信,以获取或发送数据。以下是对AJAX的主要组成部分和概念的概述࿱…...
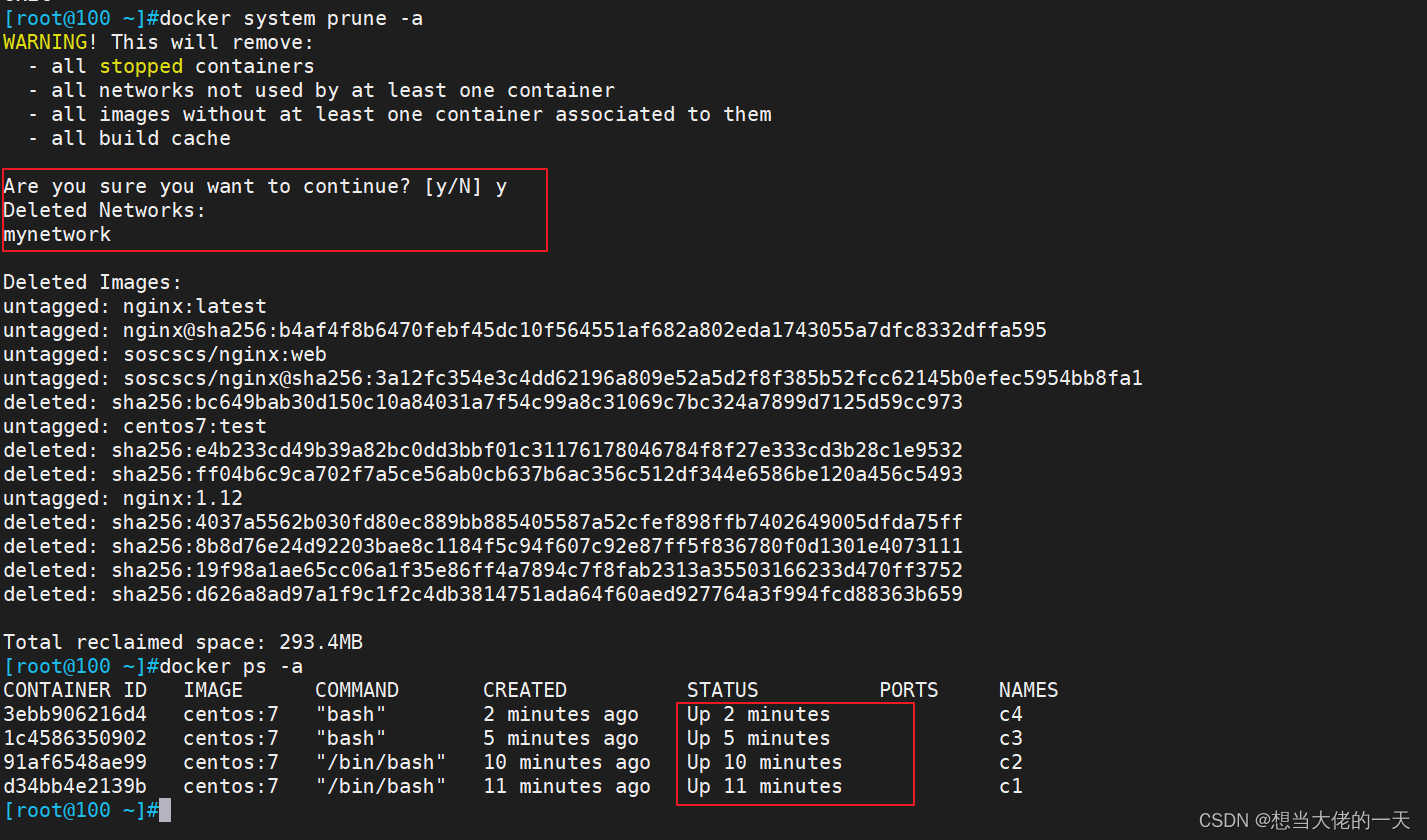
[云原生1.]Docker数据管理与Cgroups资源控制管理
文章目录 1. Docker的数据管理1.1 数据卷1.1.1 示例 1.2 数据卷容器 2. 容器互联3. Cgroups资源控制管理3.1 简介3.2 cgroups的主要功能3.3 cpu时间片的简单介绍3.4 对CPU使用的限制3.4.1 对CPU使用的限制(基于单个容器)3.4.2 对CPU使用的限制࿰…...

【华为OD机试】HJ68 成绩排序
描述 给定一些同学的信息(名字,成绩)序列,请你将他们的信息按照成绩从高到低或从低到高的排列,相同成绩 都按先录入排列在前的规则处理。 例示: jack 70 peter 96 Tom 70 smith 67 从高到低 成…...
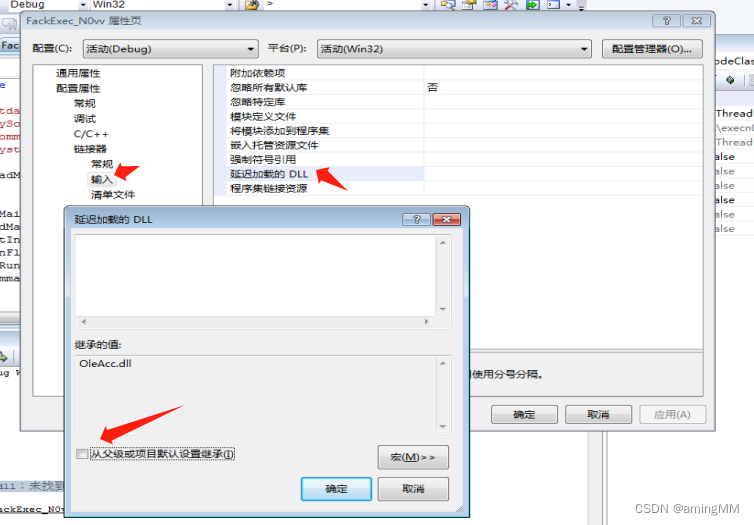
红队专题-从零开始VC++C/S远程控制软件RAT-MFC-[5]客户端与服务端连接
红队专题 招募六边形战士队员端操作系统SystemInfo类获取系统信息发送系统信息头文件声明头文件调用 未找到来自 OleAcc.dll 的导入LINK 招募六边形战士队员 一起学习 代码审计、安全开发、web攻防、逆向等。。。 私信联系 端 发送连接->进入主线程->返回socket->…...

Windows Server服务器下的Linux子系统
Windows、Linux看似死敌一对,但其实微软对于开源实业还是相当支持的,Windows 10系统内就首次内置了一个Linux子系统(Windows Subsystem for Linux/WSL),允许开发者模拟Linux环境,而且有需要的可以直接从Windows应用商店下载SUSE、…...

git初学者使用教程(包含Android studio中git使用)
文章目录 1、登录 / 注册git账号2、创建git仓库3、设置git的用户名和邮箱4、创建git仓库5、已有仓库推送代码到远程仓库6、进阶使用,命令行和Android studio软件使用1. 克隆(Clone)源码仓库2. 查看仓库状态(Status)3. …...

【Java】正则表达式,校验数据格式的合法性。
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 正则表达式 正则表达式: ①可以校…...
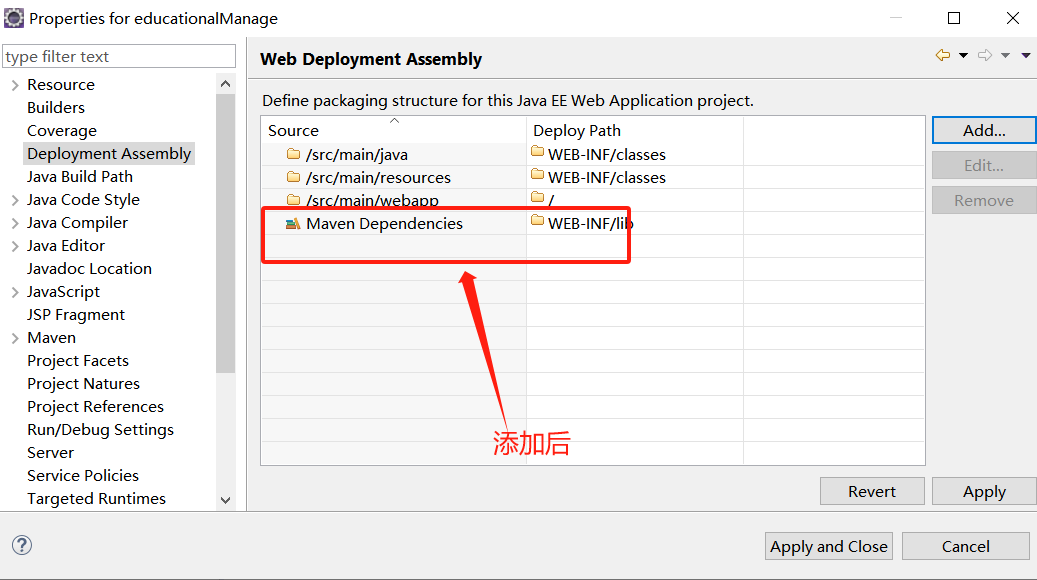
基于SSM的教务管理系统运行教程
文章目录 1、前期必备1.1、所需软件版本说明1.2、下载源码1.3、下载开发工具1.4、下载JDK并配置环境变量1.5、安装数据库和数据库管理工具1.6、安装配置Maven 2、将SQL文件导入到数据库2.1、新建MySQL连接2.2、新建数据库并导入SQL 3、用Eclipse运行程序3.1、导入educationalMa…...
、Docker-compose简单了解)
Docker(六)、Docker-compose简单了解
Docker-compose简单了解 一、简单了解-->概述一)、官方提供的容器编排工具:Docker-compose特点:二)、Docker-compose安装三)、浅实践下四).以上步骤遇到问题及解决 一、简单了解–>概述 Docker-comp…...

互联网Java工程师面试题·Java 面试篇·第一弹
目录 1、Java 中能创建 volatile 数组吗? 2、volatile 能使得一个非原子操作变成原子操作吗? 3、volatile 修饰符的有过什么实践? 4、volatile 类型变量提供什么保证? 5、10 个线程和 2 个线程的同步代码,哪个更容…...

基于材料生成优化的BP神经网络(分类应用) - 附代码
基于材料生成优化的BP神经网络(分类应用) - 附代码 文章目录 基于材料生成优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.材料生成优化BP神经网络3.1 BP神经网络参数设置3.2 材料生成算法应用 4.测试结果…...

tcp/ip协议和opc协议对比详解
TCP/IP协议和OPC协议是两种重要的网络协议,它们在不同的网络层级上运行,并为数据传输和通信提供了不同的功能。 TCP/IP协议(Transmission Control Protocol/Internet Protocol,传输控制协议/互联网协议)是互联网通信的…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
