代码随想录算法训练营第二十九天 | 回溯算法总结
代码随想录算法训练营第二十九天 | 回溯算法总结
1. 组合问题
1.1 组合问题
在77. 组合中,我们开始用回溯法解决第一道题目:组合问题。
回溯算法跟k层for循环同样是暴力解法,为什么用回溯呢?回溯法的魅力,用递归控制for循环嵌套的数量!
把回溯问题抽象为树形结构,如图:

可以直观的看出其搜索的过程:for循环横向遍历,递归纵向遍历,回溯不断调整结果集。
优化回溯算法只有剪枝一种方法,树形结构如图:

剪枝精髓是:for循环在寻找起点的时候要有一个范围,如果这个起点到集合终止之间的元素已经不够题目要求的k个元素了,就没有必要搜索了。
在for循环上做剪枝操作是回溯法剪枝的常见套路! 后面的题目还会经常用到。
1.2 组合总和
组合总和(一)
在216. 组合总和 III中,相当于在77. 组合加了一个元素总和的限制。
树形结构如图:

整体思路还是一样的,本题的剪枝会好想一些,即:已选元素总和如果已经大于n(题中要求的和)了,那么往后遍历就没有意义了,直接剪掉,如图:

在本题中,依然还可以有一个剪枝,就是77. 组合剪枝中提到的,对for循环选择的起始范围的剪枝。所以剪枝的代码可以在for循环加上 i <= 9 - (k - path.size()) + 1的限制!
组和总和(二)
在39. 组合总和中讲解的组合总和问题,和77.组合与216.组合总和III的区别是:本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。
本题还需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?
如果是一个集合来求组合的话,就需要startIndex,例如:77.组合与216.组合总和III
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:17. 电话号码的字母组合
以上我只是说求组合的情况,如果是排列问题,又是另一套分析的套路。
树形结构如下:

本题的剪枝优化,如下:
for (int i = idx; i < candidates.length; i++) {// 如果 sum + candidates[i] > target 就终止遍历if (sum + candidates[i] > target) break;
优化后树形结构如下:

组合总和(三)
在组合总和II中集合元素会有重复,但要求解集不能包含重复的组合。
所以难就难在去重问题上了。
为了讲解这个去重问题,科普两个概:“树枝去重”和“树层去重”。
“树枝去重”和“树层去重”出自代码随想录Carl
都知道组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上“使用过”,一个维度是同一树层上“使用过”。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。

我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
对于去重,其实排列和子集问题也是一样的道理。
1.3 多个集合求组合
在17.电话号码的字母组合中,开始用多个集合来求组合,还是熟悉的模板题目,但是有一些细节。
例如这里for循环,可不像是在77.组合与216.组合总和III中从startIndex开始遍历的。
因为本题每一个数字代表的是不同集合,也就是求不同集合之间的组合,而77.组合与216.组合总和III都是是求同一个集合中的组合!
树形结构如下:

1.4 切割问题
在131.分割回文串中,我们开始讲解切割问题,虽然最后代码看起来好像是一道模板题,但是从分析到学会套用这个模板,是比较难的。
以下是几个难点:
- 切割问题其实类似组合问题
- 如何模拟那些切割线
- 切割问题中递归如何终止
- 在递归循环中如何截取子串
- 如何判断回文
如果想到了用求解组合问题的思路来解决切割问题本题就成功一大半了,接下来就可以对着模板照葫芦画瓢。
但后续如何模拟切割线,如何终止,如何截取子串,其实都不好想,最后判断回文算是最简单的了。
除了这些难点,本题还有细节,例如:切割过的地方不能重复切割所以递归函数需要传入i + 1。
树形结构如下:

子集问题
子集问题(一)
在78. 子集中讲解了子集问题,在树形结构中子集问题是要收集所有节点的结果,而组合问题是收集叶子节点的结果。
如图:

认清这个本质之后,今天的题目就是一道模板题了。
本题其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了,本来我们就要遍历整棵树。
不写终止条件会不会无限递归呢?
并不会,因为每次递归的下一层就是从i+1开始的。
如果要写终止条件,注意:result.add(new ArrayList<>(path));要放在终止条件的上面,如下:
result.add(new ArrayList<>(path));//「遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合」。if (startIndex >= nums.length){ //终止条件可不加return;}
子集问题(二)
在90.子集II中,开始针对子集问题进行去重。
本题就是78. 子集的基础上加上了去重,去重我们在组合总和II也讲过了,一样的套路。
树形结构如下:

递增子序列
在491.递增子序列中,处处都能看到子集的身影,但处处是陷阱,值得好好琢磨琢磨!
树形结构如下:

很多同学都会把这道题目和90.子集II混在一起。
2. 排列问题
排列问题(一)
46. 全排列又不一样了。
排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
如图:

大家此时可以感受出排列问题的不同:
- 每层都是从0开始搜索而不是startIndex
- 需要used数组记录path里都放了哪些元素了
排列问题(二)
排列问题也要去重了,在47. 全排列 II中又一次强调了“树层去重”和“树枝去重”。
树形结构如下:

这道题目神奇的地方就是used[i - 1] = = false也可以,used[i - 1] = = true也可以!
本题used数组即是记录path里都放了哪些元素,同时也用来去重,一举两得。
相关文章:

代码随想录算法训练营第二十九天 | 回溯算法总结
代码随想录算法训练营第二十九天 | 回溯算法总结 1. 组合问题 1.1 组合问题 在77. 组合中,我们开始用回溯法解决第一道题目:组合问题。 回溯算法跟k层for循环同样是暴力解法,为什么用回溯呢?回溯法的魅力,用递…...
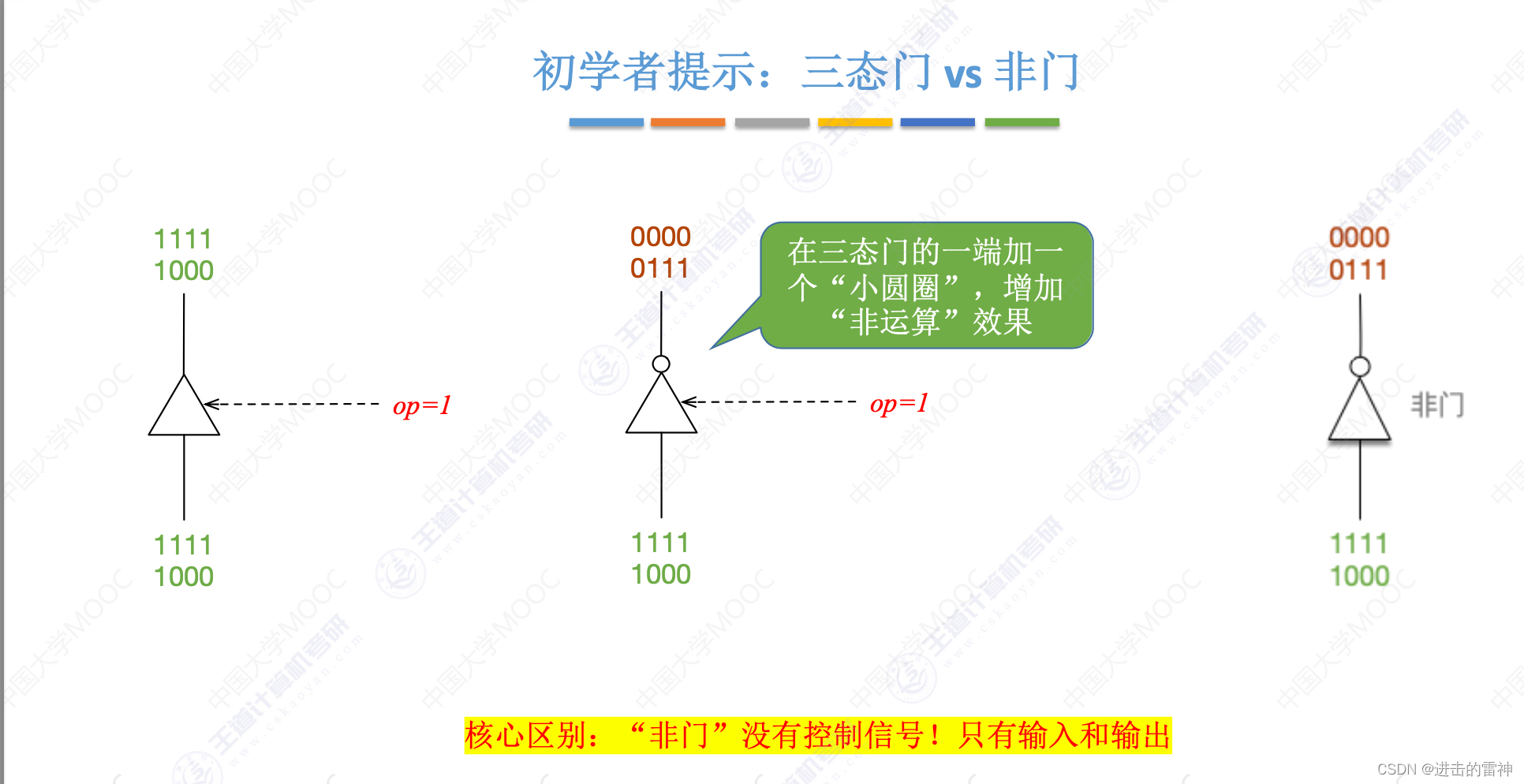
运算方法和运算电路
一、逻辑门电路 1、逻辑门电路基础总结 2、异或运算妙用 3、逻辑常用公式 二、加法器(重点) 1、标志位的生成原理 2、加法器总结 三、多路门选择器,三态门...
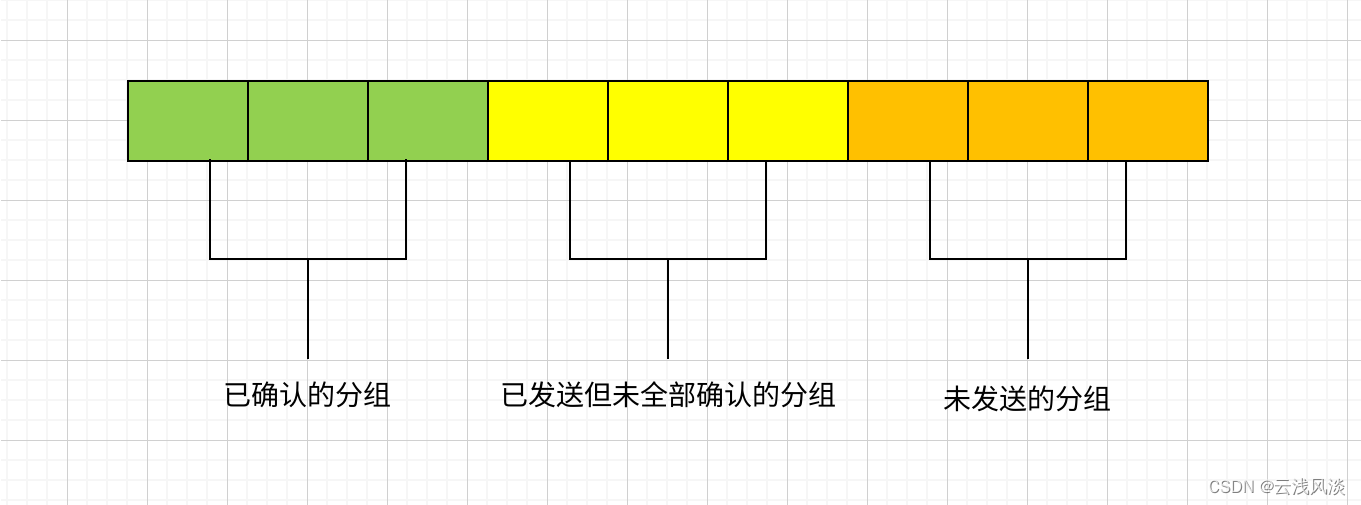
计算机网络篇之TCP滑动窗口
文章目录 前言概述 前言 在网络数据传输时,若传输的原始数据包比较大,会将数据包分解成多个数据包进行发送。需要对数据包确认后,才能发送下一个数据包。在等待确认包的这个过程浪费了大量的时间,不过还好TCP引入了滑动窗口的概念…...

本地安装telepresence,访问K8S集群 Mac(m1) 非管理員
kubeconfig 一.安装telepresence 1.安装 Telepresence Quickstart | Telepresence (1)brew install datawire/blackbird/telepresence 2.配置 目录kubectl 将使用默认的 kubeconfig 文件:$HOME/.kube/config 创建文件夹&…...
 — 训练机器学习模型用GPU还是NUP更有优势(基于文心一言的回答))
今日思考(2) — 训练机器学习模型用GPU还是NUP更有优势(基于文心一言的回答)
前言 深度学习用GPU,强化学习用NPU。 1.训练深度学习模型,强化学习模型用NPU还是GPU更有优势 在训练深度学习模型时,GPU相比NPU有优势。GPU拥有更高的访存速度和更高的浮点运算能力,因此更适合深度学习中的大量训练数据、大量矩阵…...

8.3 C++ 定义并使用类
C/C语言是一种通用的编程语言,具有高效、灵活和可移植等特点。C语言主要用于系统编程,如操作系统、编译器、数据库等;C语言是C语言的扩展,增加了面向对象编程的特性,适用于大型软件系统、图形用户界面、嵌入式系统等。…...

Git学习笔记——超详细
Git笔记 安装git: apt install git 创建版本库: git init 添加文件到版本库: git add 文件 提交文件到仓库: git commit -m “注释” 查看仓库当前的状态信息: git status 查看修改内容和之前版本的区别&am…...
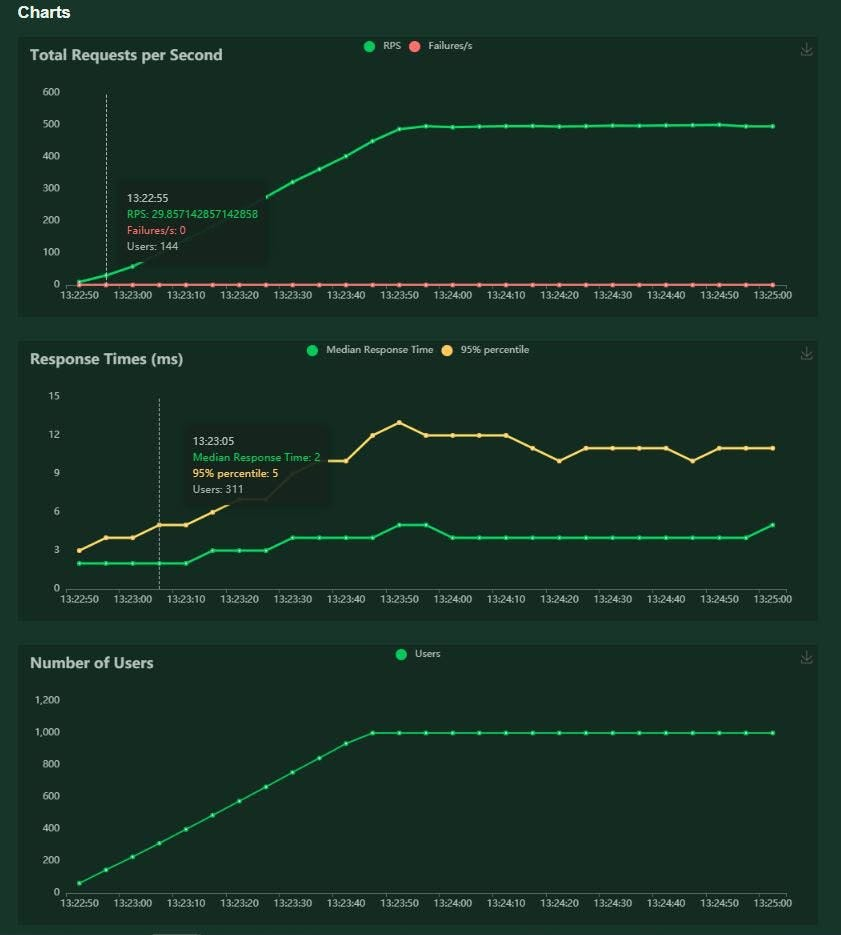
Locust负载测试工具实操
本中介绍如何使用Locust为开发的服务/网站执行负载测试。 Locust 是一个开源负载测试工具,可以通过 Python 代码构造来定义用户行为,避免混乱的 UI 和臃肿的 XML 配置。 步骤 设置Locust。 在简单的 HTTP 服务上模拟基本负载测试。 准备条件 Python…...
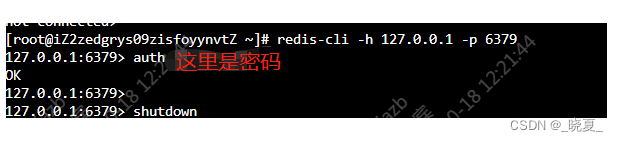
关闭mysql,关闭redis服务
1. 关闭redis服务: 查询redis安装目录: whereis redis which redis find / -name redis 关闭redis服务: redis-cli -h 127.0.0.1 -p 6379 auth 输入密码 shutdown 关闭redis服务 2. 关闭mysql服务: 查询mysql安装目录&…...

微机原理:汇编语言语句类型与格式
文章目录 壹、语句类型1、语句分类2、常用伪代码和运算符2.1数据定义伪指令2.1.1字节定义伪指令DB(8位)2.1.2字定义伪指令DW(16位)2.1.3双字节伪指令DD2.1.4 多字节定义DF/DQ/DT(了解) 2.2 常用运算符2.2.1…...

iOS Flutter Engine源码调试和修改
iOS Flutter Engine源码调试和修改 1. 前提:2. 步骤:3. 参考资料 1. 前提: 已将成功安装deop_tools工具已经通过gclient命令同步好flutter engine源码 2. 步骤: 进入engine/src目录 创建flutter engine构建文件 真机文件debug模式: ./flu…...
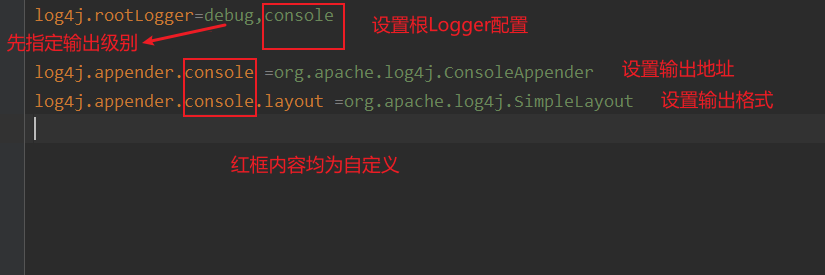
Java日志系统之Log4j
目录 Log4J Log4j的简单使用 日志级别 Log4j的组件 Loggers Appenders Layout Layout格式 设置配置文件加载 配置文件解析 Log4J 是Apache下开源的日志框架 Log4j的简单使用 Testpublic void testLog4J(){Logger logger Logger.getLogger(Log4jTest.class);logger…...

Windows11系统安装WSL教程
WSL,全称Windows Subsystem for Linux,是微软官方提供的可以在Windows上直接运行的Linux环境,包括大多数命令行工具、程序和应用,由系统底层虚拟机平台支持。 开启相关服务 1、控制面板-启用或关闭Windows功能 2、勾选以下两个…...

总结一下vue中v-bind的常见用法
文章目录 🐕前言:🏨简述一下v-bind命令🧸其它写法1.还是当成字符串🦓其它写法2.当成对象来使用 🐕前言: 本篇博客主要总结一下v-bind命令在vue中的常见用法(看完即懂) …...
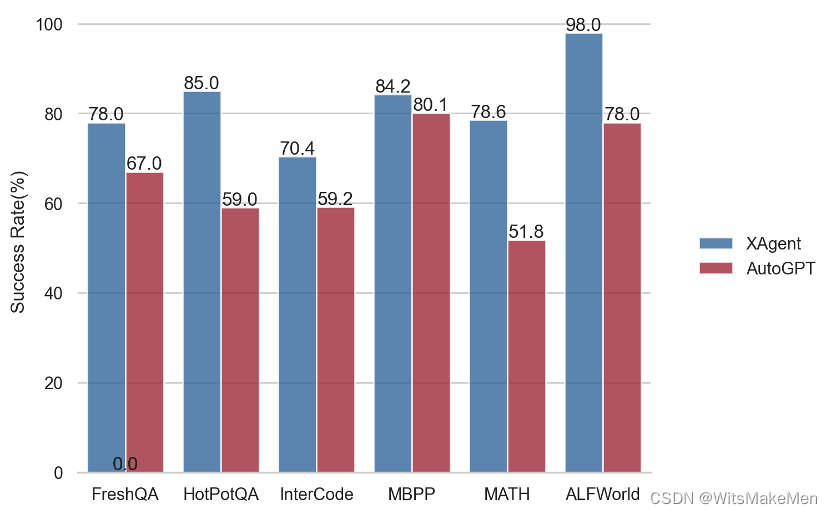
全面超越AutoGPT,面壁智能联合清华NLP实验室开源大模型「超级英雄」XAgent
近日,国内领先的人工智能大模型公司面壁智能又放大招,联合清华大学 NLP 实验室共同研发并推出大模型「超级英雄」——XAgent。 通过任务测试,XAgent 在真实复杂任务的处理能力已全面超越 AutoGPT。 现已在 GitHub 正式开源,地址 …...
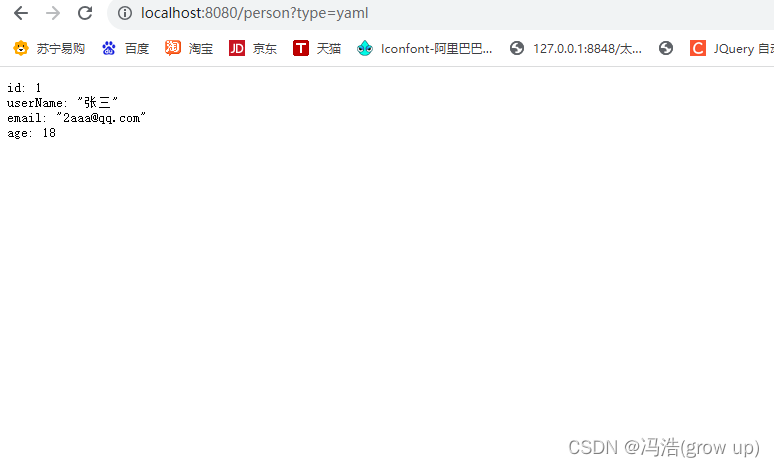
springBoot--web--http缓存机制测试
springBoot--web--http缓存机制测试 前言1、多端内容适配基于请求头内容协商(默认开启)基于请求参数内容协商(需要开启) 2、默认返回json数据3、设置返回xml数据导入jackson-dataformat-xml包在类文件中添加注解 JacksonXmlRootEl…...

免费活动】11月4日敏捷武林上海站 | Scrum.org CEO 亲临现场
活动介绍 过去的几年里,外界的风云变幻为我们的生活增添了一些不一样的色彩。在VUCA世界的浪潮里,每一个人都成为自己生活里的冒险家。面对每一次的变化,勇于探索未知,迎接挑战,努力追逐更好的自己。 七月࿰…...
VSCode搭建ESP32 ESP-IDF开发环境-Windows
陈拓 2023/10/09-2023/10/14 1. 安装Windows系统下的ESP32 ESP-IDF开发环境 见《Windows系统安装ESP32 ESP-IDF开发环境》 Windows系统安装ESP32 ESP-IDF开发环境-CSDN博客Windows系统安装ESP32 ESP-IDF开发环境。https://blog.csdn.net/chentuo2000/article/details/1339225…...
)
Java可重入锁(GPT编写)
Java可重入锁是Java并发编程中常用的一种锁机制,它可以允许同一个线程多次获取同一个锁,从而避免死锁和其他并发问题。在本篇博客中,我们将对Java可重入锁的源码进行分析,以便更好地理解它的实现原理和使用方法。 Java可重入锁的…...

京东数据平台:2023年9月京东净水器行业品牌销售排行榜!
鲸参谋监测的京东平台9月份净水器市场销售数据已出炉! 根据鲸参谋平台的数据显示,今年9月份,京东平台净水器的销量为64万,环比下滑约9%,同比下滑约16%;销售额为5.2亿,环比下滑约12%,…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
