卷积神经网络CNN学习笔记-卷积计算Conv2D函数的理解
目录
- 1.全连接层存在的问题
- 2.卷积运算
- 3.填充(padding)
- 3.1填充(padding)的意义
- 4.步幅(stride)
- 5.三维数据的卷积运算
- 6.结合方块思考
- 7.批处理
- 8.Conv2D函数解析
- 9.conv2d代码
- 9.1 stride=1
- 9.2 stride=2
- 参考文章
1.全连接层存在的问题
在全连接层中,相邻层的神经元全部连接在一起,输出的数量可以任意决定。全连接层存在什么问题呢?那就是数据的形状被“忽视”了。比如,输入数据是图像时,图像通常是高、长、通道方向上的3维形状。但是,向全连接层输入时,需要将3维数据拉平为1维数据。实际上,前面提到的使用了MNIST数据集的例子中,输入图像就是1通道、高28像素、长28像素的(1, 28, 28)形状,但却被排成1列,以784个数据的形式输入到最开始的Affine层。图像是3维形状,这个形状中应该含有重要的空间信息。比如,空间上邻近的像素为相似的值、RBG的各个通道之间分别有密切的关联性、相距较远的像素之间没有什么关联等,3维形状中可能隐藏有值得提取的本质模式。但是,因为全连接层会忽视形状,将全部的输入数据作为相同的神经元(同一维度的神经元)处理,所以无法利用与形状相关的信息。而卷积层可以保持形状不变。当输入数据是图像时,卷积层会以3维数据的形式接收输入数据,并同样以3维数据的形式输出至下一层。因此,在CNN中,可以(有可能)正确理解图像等具有形状的数据。另外,CNN 中,有时将卷积层的输入输出数据称为特征图(feature map)。其中,卷积层的输入数据称为输入特征图(input feature map),输出数据称为输出特征图(output feature map)。本文中将“输入输出数据”和“特征图”作为含义相同的词使用.
2.卷积运算
卷积层进行的处理就是卷积运算。卷积运算相当于图像处理中的“滤波器运算”。在介绍卷积运算时,我们来看一个具体的例子(图7-3)。

如图7-3所示,卷积运算对输入数据应用滤波器。在这个例子中,输入数据是有高长方向的形状的数据,滤波器也一样,有高长方向上的维度。假设用(height, width)表示数据和滤波器的形状,则在本例中,输入大小是(4, 4),滤波器大小是(3, 3),输出大小是(2, 2)。另外,有的文献中也会用“核”这个词来表示这里所说的“滤波器”。现在来解释一下图7-3的卷积运算的例子中都进行了什么样的计算。图7-4中展示了卷积运算的计算顺序。对于输入数据,卷积运算以一定间隔滑动滤波器的窗口并应用。这里所说的窗口是指图7-4中灰色的3 × 3的部分。如图7-4所示,将各个位置上滤波器的元素和输入的对应元素相乘,然后再求和(有时将这个计算称为乘积累加运算)。然后,将这个结果保存到输出的对应位置。将这个过程在所有位置都进行一遍,就可以得到卷积运算的输出。在全连接的神经网络中,除了权重参数,还存在偏置。CNN中,滤波器的参数就对应之前的权重。并且,CNN中也存在偏置。图7-3的卷积运算的例子一直展示到了应用滤波器的阶段。包含偏置的卷积运算的处理流如图7-5所示。如图7-5所示,向应用了滤波器的数据加上了偏置。偏置通常只有1个(1 × 1)(本例中,相对于应用了滤波器的4个数据,偏置只有1个),这个值会被加到应用了滤波器的所有元素上。


3.填充(padding)
在进行卷积层的处理之前,有时要向输入数据的周围填入固定的数据(比如0等),这称为填充(padding),是卷积运算中经常会用到的处理。比如,在图7-6的例子中,对大小为(4, 4)的输入数据应用了幅度为1的填充。“幅度为1的填充”是指用幅度为1像素的0填充周围。

如图7-6所示,通过填充,大小为(4, 4)的输入数据变成了(6, 6)的形状。然后,应用大小为(3, 3)的滤波器,生成了大小为(4, 4)的输出数据。这个例子中将填充设成了1,不过填充的值也可以设置成2、3等任意的整数。在图7-5的例子中,如果将填充设为2,则输入数据的大小变为(8, 8);如果将填充设为3,则大小变为(10, 10)
3.1填充(padding)的意义
使用填充主要是为了调整输出的大小。比如,对大小为(4, 4)的输入数据应用(3, 3)的滤波器时,输出大小变为(2, 2),相当于输出大小比输入大小缩小了 2个元素。这在反复进行多次卷积运算的深度网络中会成为问题。为什么呢?因为如果每次进行卷积运算都会缩小
空间,那么在某个时刻输出大小就有可能变为 1,导致无法再应用卷积运算。为了避免出现这样的情况,就要使用填充。在刚才的例子中,将填充的幅度设为 1,那么相对于输入大小(4, 4),输出大小也保持为原来的(4, 4)。因此,卷积运算就可以在保持空间大小不变
的情况下将数据传给下一层。
4.步幅(stride)

在图7-7的例子中,对输入大小为(7, 7)的数据,以步幅2应用了滤波器。通过将步幅设为2,输出大小变为(3, 3)。像这样,步幅可以指定应用滤波器的间隔。综上,增大步幅后,输出大小会变小。而增大填充后,输出大小会变大。如果将这样的关系写成算式,会如何呢?接下来,我们看一下对于填充和步幅,如何计算输出大小。这里,假设输入大小为(H, W),滤波器大小为(FH, FW),输出大小为(OH, OW),填充为P,步幅为S。此时,输出大小可通过式(7.1)进行计算。
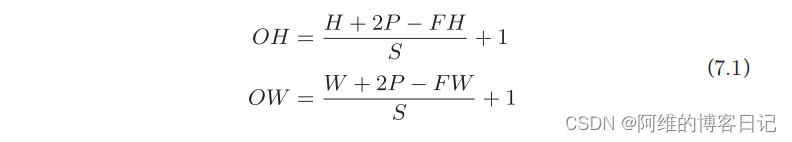

5.三维数据的卷积运算
之前的卷积运算的例子都是以有高、长方向的2维形状为对象的。但是,图像是3维数据,除了高、长方向之外,还需要处理通道方向。这里,我们按照与之前相同的顺序,看一下对加上了通道方向的3维数据进行卷积运算的例子。图7-8是卷积运算的例子,图7-9是计算顺序。这里以3通道的数据为例,展示了卷积运算的结果。和2维数据时(图7-3的例子)相比,可以发现纵深方向(通道方向)上特征图增加了。通道方向上有多个特征图时,会按通道进行输入数据和滤波器的卷积运算,并将结果相加,从而得到输出。


需要注意的是,在3维数据的卷积运算中,输入数据和滤波器的通道数要设为相同的值。在这个例子中,输入数据和滤波器的通道数一致,均为3。滤波器大小可以设定为任意值(不过,每个通道的滤波器大小要全部相同)。这个例子中滤波器大小为(3, 3),但也可以设定为(2, 2)、(1, 1)、(5, 5)等任意值。再强调一下,通道数只能设定为和输入数据的通道数相同的值(本例中为3)。
6.结合方块思考
将数据和滤波器结合长方体的方块来考虑,3维数据的卷积运算会很容易理解。方块是如图7-10所示的3维长方体。把3维数据表示为多维数组时,书写顺序为(channel, height, width)。比如,通道数为C、高度为H、长度为W的数据的形状可以写成(C, H, W)。滤波器也一样,要按(channel, height, width)的顺序书写。比如,通道数为C、滤波器高度为FH(Filter Height)、长度为FW(Filter Width)时,可以写成(C, FH, FW)。

在这个例子中,数据输出是1张特征图。所谓1张特征图,换句话说,就是通道数为1的特征图。那么,如果要在通道方向上也拥有多个卷积运算的输出,该怎么做呢?为此,就需要用到多个滤波器(权重)。用图表示的话,如图7-11所示。

图7-11中,通过应用FN个滤波器,输出特征图也生成了FN个。如果将这FN个特征图汇集在一起,就得到了形状为(FN, OH, OW)的方块。将这个方块传给下一层,就是CNN的处理流。如图 7-11 所示,关于卷积运算的滤波器,也必须考虑滤波器的数量。因此,作为4维数据,滤波器的权重数据要按(output_channel, input_channel, height, width)的顺序书写。比如,通道数为3、大小为5 × 5的滤波器有20个时,可以写成(20, 3, 5, 5)。卷积运算中(和全连接层一样)存在偏置。在图7-11的例子中,如果进一步追加偏置的加法运算处理,则结果如下面的图7-12所示。图7-12中,每个通道只有一个偏置。这里,偏置的形状是(FN, 1, 1),滤波器的输出结果的形状是(FN, OH, OW)。这两个方块相加时,要对滤波
器的输出结果(FN, OH, OW)按通道加上相同的偏置值。另外,不同形状的方块相加时,可以基于NumPy的广播功能轻松实现(1.5.5节)。

7.批处理
神经网络的处理中进行了将输入数据打包的批处理。之前的全连接神经网络的实现也对应了批处理,通过批处理,能够实现处理的高效化和学习时对mini-batch的对应。我们希望卷积运算也同样对应批处理。为此,需要将在各层间传递的数据保存为4维数据。具体地讲,就是按(batch_num, channel, height, width)的顺序保存数据。比如,将图7-12中的处理改成对N个数据进行批处理时,数据的形状如图7-13所示。图7-13的批处理版的数据流中,在各个数据的开头添加了批用的维度。像这样,数据作为4维的形状在各层间传递。这里需要注意的是,网络间传递的是4维数据,对这N个数据进行了卷积运算。也就是说,批处理将N次的处理汇总成了1次进行.

8.Conv2D函数解析
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode=‘zeros’, device=None, dtype=None)
-
in_channels:输入通道数,也就是图7-13中的C,指示多少张H×W -
out_channels:输出通道数,也就是图7-13中的FN -
kernel_size:卷积核大小,也就是滤波器大小,可以自定义为num或者是num1×num2
当kernel_size为num时,表示卷积核大小为num×num. -
stride:当stride=1,卷积核如图9-1所示移动,第一行卷积完毕时,到第二行卷积,其中卷积核每次卷积在水平方向上移动时相差stride=1个格子,垂直方向移动时,相差stride=1个格子.当stride=2时,卷积核如图9-2所示移动,第一行卷积完毕时,从第一行蹦到第三行卷积.水平方向移动时相隔stride=2个格子移动,垂直方向上移动时,相差stride=2个格子移动. -
padding:padding=0是表示不填充任何0,padding=1表示从(A,A)大小填充为(A+2,A+2),因为是上下左右同时填充1个,所以都要加2. -
dilation,这个参数涉及到空洞卷积的东西,但是这个我不太理解,只知道dilation=1时就是我们正常卷积.

空洞卷积参考
👉:🔗深入理解空洞卷积
👉:🔗Convolution arithmetic -
groups分组卷积,一般取值groups = in_channels.这个不太理解,只知道取值一般就是这样,原因以后再补充.现在研一啥也不懂 -
bias即是否要添加偏置参数作为可学习参数的一个,默认为True。 -
padding_mode='zeros':即padding的模式,默认采用零填充
9.conv2d代码
9.1 stride=1

import torch
import torch.nn as nn# 设定一个[1, 3, 5, 5]的输入
input = torch.Tensor([[[[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5]],[[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5]],[[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5]]]])
# 设定一个卷积
conv = nn.Conv2d(in_channels=3,out_channels=3,kernel_size=3,#这里的kernel_size=3和kernel_size=(3,3)意思一样stride=1,padding=0,# 注意,这里padding=0意思是不填充任何数字# 若padding=1,则举个例子,原来的(3,3)是填充为(5,5),而非(4,4)dilation=1,groups=3)# 设定卷积的权重数值
conv.weight.data = torch.Tensor([[[[1, 1, 1],[1, 1, 1],[1, 1, 1]]],[[[2, 2, 2],[2, 2, 2],[2, 2, 2]]],[[[3, 3, 3],[3, 3, 3],[3, 3, 3]]]])
# 利用卷积得到输出
output = conv(input)
print(output)
9.2 stride=2

import torch
import torch.nn as nn# 设定一个[1, 3, 5, 5]的输入
input = torch.Tensor([[[[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5]],[[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5]],[[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5],[1, 2, 3, 4, 5]]]])
# 设定一个卷积
conv = nn.Conv2d(in_channels=3,out_channels=3,kernel_size=3,stride=2,padding=0,dilation=1,groups=3)# 设定卷积的权重数值
conv.weight.data = torch.Tensor([[[[1, 1, 1],[1, 1, 1],[1, 1, 1]]],[[[2, 2, 2],[2, 2, 2],[2, 2, 2]]],[[[3, 3, 3],[3, 3, 3],[3, 3, 3]]]])
# 利用卷积得到输出
output = conv(input)
print(output)参考文章
[1]🔗Pytorch的nn.Conv2d详解
[2]🔗深入理解空洞卷积
[3]🔗Convolution arithmetic
相关文章:

卷积神经网络CNN学习笔记-卷积计算Conv2D函数的理解
目录 1.全连接层存在的问题2.卷积运算3.填充(padding)3.1填充(padding)的意义 4.步幅(stride)5.三维数据的卷积运算6.结合方块思考7.批处理8.Conv2D函数解析9.conv2d代码9.1 stride19.2 stride2 参考文章 1.全连接层存在的问题 在全连接层中,相邻层的神经元全部连接…...

收藏,安装报错信息汇总,MacOS上安装Adobe等软件/插件报错问题解决合集
打开允许“允许任何来源” 如何打开允许任何来源?在 Finder 菜单栏选择 【前往】 – 【实用工具 】,找到【终端】程序,双击打开,在终端窗口中输入:sudo spctl --master-disable 输入代码后,按【return 回车…...
: invalid pointer解决方案)
Qt 报错:munmap_chunk(): invalid pointer解决方案
问题 在用Qt写程序的时候。报了munmap_chunk(): invalid pointer这个错误消息。 造成原因 在 Qt 程序中,这种错误可能出现在多种情况下,以下几点是容易造成此问题的原因: 函数未实现返回值:函数有返回值,但函数体中…...

【Java题】实现继承和多态的例子
一:题目 1.员工类Employee: (1)私有成员变量:姓名,年龄,工资 (2)提供无参,有参构造 (3)成员方法:work()方法——员工工作 …...
‘conda‘ 不是内部或外部命令,也不是可运行的程序 或批处理文件。
原因:环境变量没有正确添加解决:我的电脑—右键属性—高级系统设置—环境变量—系统变量—Path—双击进入—新建,去安装Anaconda的目录下,找到Library中的bin,将此时的路径粘贴到此处...

C1N短网址 - 是如何做到行业领先的
今天从技术角度来聊下短网址的一些事情,市面上的短网址发展基本上经历了几个阶段。 短网址发展的几个阶段: 第一阶段:网址缩短,很纯粹的功能,各个大小公司都在做,门槛很低。典型代表:百度短网…...
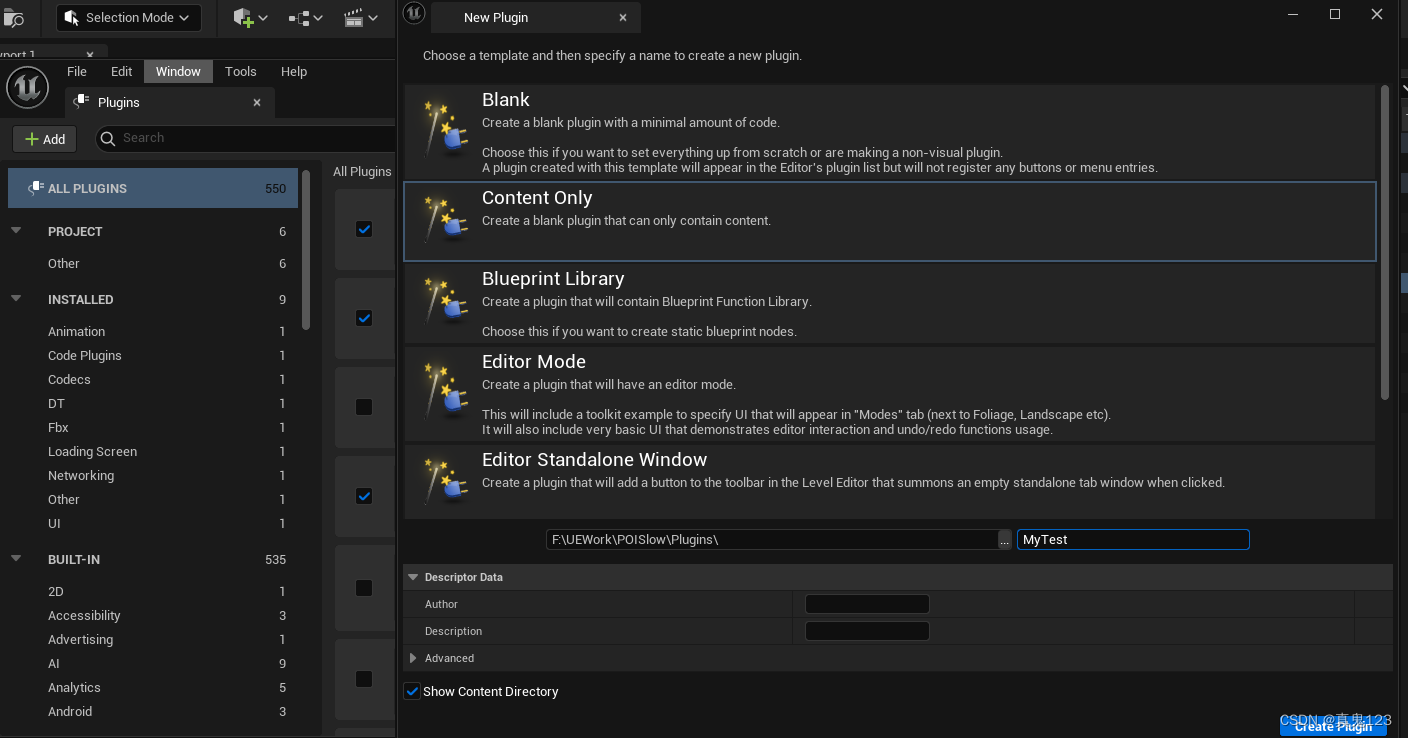
【UE5】引入C++插件Plugins不在UE里出现
原因 未编译过C 原项目为蓝图项目,或者虽然为C项目,但并为编译过C. 解决 创建一个C脚本,让编辑器重启重新编译一遍。 如还不行,则打开Plugins插件面板,创建一个空的新的插件,再让引擎自动重启重新编译…...

第三部分:JavaScript
一:JavaScript介绍 JavaScript语言诞生主要是完成页面的数据验证。因此它运行在客户端,需要运行浏览器来解析执行JavaScript代码。 JavaScript是Net scape网景公司的产品,最早取名为LiveScript;为了吸引更多的程序员,更…...

Redis 命令—— 超详细操作演示!!!
内存数据库 Redis7 三、Redis 命令3.1 Redis 基本命令3.2 Key 操作命令3.3 String 型 Value 操作命令3.4 Hash 型 Value 操作命令3.5 List 型 Value 操作命令3.6 Set 型 Value 操作命令3.7 有序Set 型 Value 操作命令3.8 benchmark 测试工具3.9 简单动态字符串SDS3.10 集合的底…...

工业自动化控制通信协议Profinet系列-3、CoDeSys软PLC方案介绍
工业自动化控制通信协议Profinet系列-3、CoDeSys软PLC方案介绍 文章目录 工业自动化控制通信协议Profinet系列-3、CoDeSys软PLC方案介绍一、前言二、Profinet搭建资料收集三、CoDeSys系列四、接下来 一、前言 之前在树莓派desktop上已经成功编译运行测试程序,但是还…...
[补题记录] Atcoder Beginner Contest 293(E)
URL:https://atcoder.jp/contests/abc293 目录 E Problem/题意 Thought/思路 Code/代码 E Problem/题意 给出 A、X、M,求 。 Thought/思路 一开始想等比数列求和,但是 m 不保证是质数,所以不能用。 假设 dp[x] 表示&…...
介绍-model.matrix)
R语言有关模型方面的函数(model.)介绍-model.matrix
R语言有关模型方面的函数(model.)介绍-model.matrix 引言model.matrix简单作用提取设计矩阵对有序因子与无序因子的处理(模型相关)手动编写contr.系列的函数写在最后引言 最近闲暇时间大量阅读了一些机器学习方面的R包源码,在此对阅读过程中的一些实用但是不常见的函数进行…...

owasp top 10
1、访问控制的崩溃: 通过身份验证的用户可以访问其他用户的信息,越权 达成方式:通过修改url、内部应用程序状态或html页面绕过 防范:除了公有资源外,默认情况下拒绝访问,严格判断权限,记录失败的…...

【FreeRTOS】【STM32】06 FreeRTOS的使用-动态创建多任务 FreeRTOS 的启动流程
主要流程参照【FreeRTOS】【STM32】06 FreeRTOS的使用-动态创建单任务 1.定义任务句柄 static TaskHandle_t AppTaskCreate_Handle NULL;2.硬件初始化 略 3.创建具体功能任务函数 见定义任务函数 4.使用xTaskCreate创建任务 xReturn xTaskCreate((TaskFunction_t )AppT…...

10月21日,每日信息差
今天是2023年10月21日,以下是为您准备的13条信息差 第一、东方物探公司与阿里云达成战略合作,逐步助力勘探行业实现智能化、自动化、绿色化和可持续化的目标 第二、九洲集团签约300MW集中式风电项目计划总投资21亿,项目达产后,预…...
)
C++学习笔记之三(函数指针、调用、动态内存、模板)
C 1、函数&指针1.1、指针函数1.2、函数指针1.2.1、函数指针作为函数的传入参数1.2.2、函数指针作为函数的返回值 2、传递2.1、值传递2.2、址传递2.3、引用传递 3、多态3.1、虚方法和抽象方法 4、动态内存5、模板5.1、函数模板5.2、类模板5.3、内联函数 1、函数&指针 1…...

【LeetCode】57. 插入区间
1 问题 给你一个 无重叠的 ,按照区间起始端点排序的区间列表。 在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。 示例 1: 输入:interval…...

实时消息传送:WebSocket实现系统后台消息实时通知
实时消息传送:WebSocket实现系统后台消息实时通知 WebSocket简介基本实现步骤后台服务器后端接口SimpMessagingTemplate MessageDto前端客户端 示例应用 在现代Web应用中,提供实时通知对于改善用户体验至关重要。WebSocket技术允许建立双向通信通道&…...
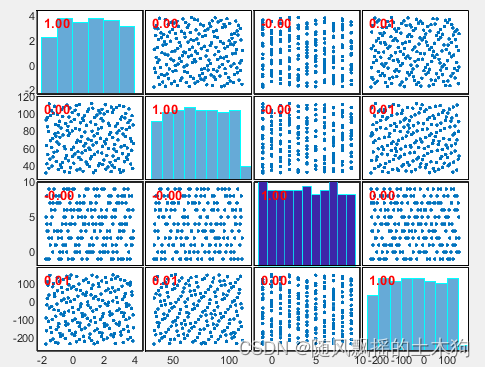
【MATLAB第79期】基于MATLAB的数据抽样合集(sobol、LHS拉丁超立方抽样、Halton、正交/均匀设计、随机rand函数)
【MATLAB第79期】基于MATLAB的数据抽样合集(sobol、LHS拉丁超立方抽样、Halton、正交/均匀设计、随机rand函数) 一、传统函数 1.指定区间随机生成数据(小数) [a b]区间随机数生成: Aa(b-a)rand(m,n) m:待生成矩阵A…...

matlab bin格式转txt输出
matlab bin格式转txt输出 clc,clear; fid fopen(\text.bin,rb); data fread(fid,Inf,int16); fclose(fid);fidfopen(\text.txt,w); fprintf(fid,%d\n,data); fclose(fid);...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...
