【算法设计技巧】分治算法
分治算法
用于设计算法的另一种常用技巧为分治算法(divide and conquer)。分治算法由两部分组成:
- 分(divide):递归解决较小的问题(当然,基准情况除外)
- 治(conquer):然后,从子问题的解构建原问题的解。
传统上,在其代码中至少含有两个递归调用的例程叫作分治算法,且一般认为子问题是不相交的(即基本上不重叠)。例如,最大子序列和问题的一个 O(N logN) 的解法,以及分治算法的经典例子:归并排序 和 快速排序,它们分别有 O(N logN) 的最坏情形以及平均时间的时间界。
分治算法的运行时间
有效的分治算法都是把问题分成一些子问题,每个子问题都是原问题的一部分,然后进行某些附加的工作以算出最后的答案。例如,归并排序对两个问题进行运算,每个问题均为原问题大小的一半,然后用到 O(N) 的附加工作。由此得到运行时间方程(带有合适初始条件):
该方程的解为 O(N logN)。下面的定理可以用来确定大部分分治算法的运行时间。
方程 T(N) = aT(N/b) + O(Nk) 的解为
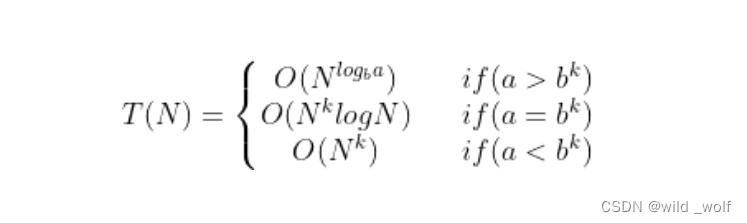
其中 a ≥ 1 以及 b >1。
最近点问题
问题的输入是平面上的点集 P。如果 p1 = (x1, y1) 和 p2 = (x2, y2),那么 p1 和 p2 间的欧几里得距离为 [ (x1 - x2)2 + (y1 - y2)2 ]1/2 。需要找出一对最近的点。这其中有可能两个点位于相同的位置,在这种情况下它们的距离为 0。
如果存在 N 个点,那么就存在 N(N-1)/2 对点间的距离。
第一种方法是检查所有这些距离,能够得到一个很短的程序,但却是花费 O(N2) 的算法,也就是穷举搜索的算法。
//计算点对间最小距离的蛮力算法
//计算点对间最小距离的蛮力算法
for (i = 0; i < numPointsInStrip; ++i)for (j = i + 1; j < numPointsInStrip; ++j)if (dist(pi, pj) < δ)δ = dist(pi, pj);
假设平面上这些点已经按照 x 的坐标排过序,这只不过顶多在最后的时间界上仅加了 O(N logN) 而已,因为整个算法都将是 O(N logN) 的,所以排序基本上没增加运行时间消耗级别。
图1 画出了一个小的样本点集 P。若这些点已按 x 坐标排序,那我们可以画一条想象的垂线,把 P 分成两半:PL 和 PR 。

最近的一对点或者都在 PL 中,或者都在 PR 中,或者一个点在 PL 中而另一个在 PR 中。这三个距离在图2 中标出。
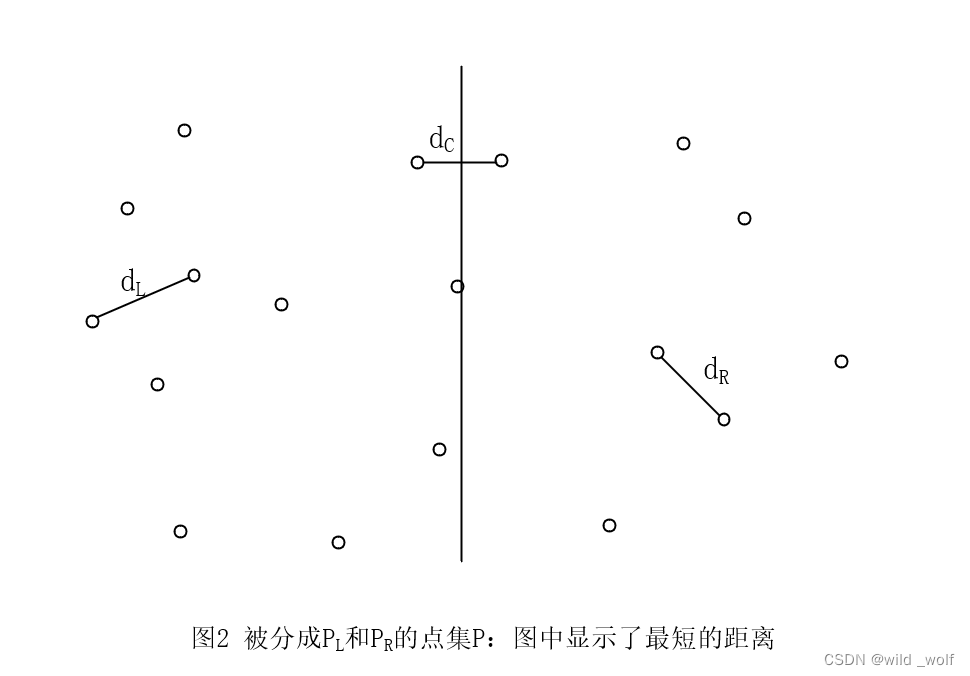
我们可以递归地计算 dL 和 dR。由于想要一个 O(N logN) 的解,因此必须能够只用 O(N) 的附加工作计算出 dC 。即,如果一个过程由两个一半大小的递归调用和附加的 O(N) 工作组成,那么总的时间将是 O(N logN)。
令 δ = min (dL, dR)。如果 dC 对 δ 有所改进,那么只需计算 dC 。如果 dC 是这样一个距离,则决定 dC 的两个点必然在分割线的 δ 距离之内,把这个条形局域叫作带(strip)。如图3 所示,这个观察结果消减了需要考虑的点的个数(此例中的 δ = dR)。
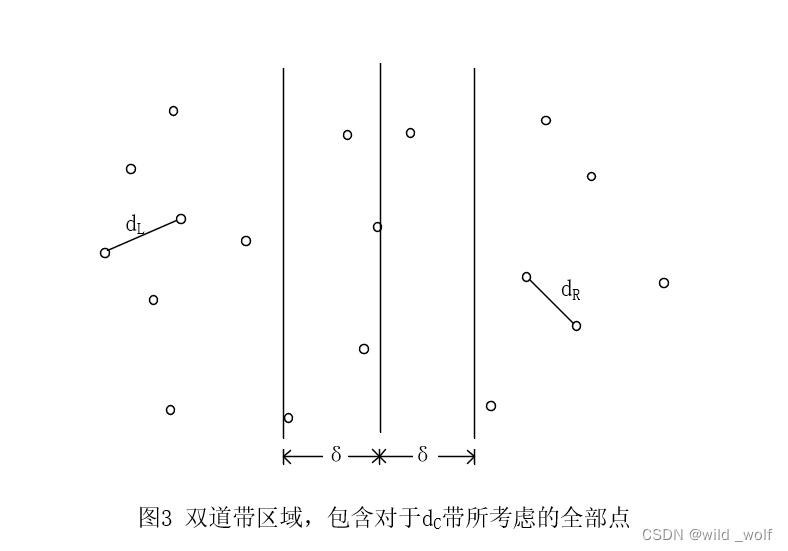
有两种方法可以用来计算 dC,由于平均只有 O(N1/2) 个点在这个带中,因此第一种方法可以以 O(N2) 时间对这些点进行蛮力计算。但在最坏情况下,所有的点可能都在这条带状区域内,因此这种算法不总能以线性时间运行。
改进算法:确定 dC 的两个点的 y 坐标之间相差最多是 δ,否则就会有 dC > δ。设带中的点按照它们的 y 坐标排序。因此,如果 pi 和 pj 的 y 坐标相差大于 δ,则可以再去继续处理 pi+1。
//最小距离的精化计算
for (i = 0; i < numPointsInStrip; ++i)for (j = i + 1; j < numPointsInStrip; ++j)if(pi and pj 's y-coordinates differ by more than δ)break; //转向下一个pielseif (dist(pi, pj) < δ)δ = dist(pi, pj);
选择问题
选择问题要求我们找出 N 个元素集合 S 中的第 k 个最小的元素。
基本的算法是简单的递归策略。设 N 大于截止点(cutoff point),元素将从截止点开始进行简单的排序,v 是选出的一个元素,叫作枢纽元(pivot)。其余元素被放在两个集合 S1 和 S2 中,S1 含有那些保证不大于 v 的元素,而 S2 包含那些不小于 v 的元素。最后,如果 k ≤ |S1|,那么 S 中的第 k 个最小的元素就可以通过递归地计算 S1 中第 k 个最小的元素而找到。如果 k = |S1| +1,则枢纽元就是第 k 个最小的元素。否则,在 S 中的第 k 个最小的元素是 S2 中的第 (k - |S1| - 1) 个最小元素。这个算法和快速排序之间的主要区别在于,这里只有一个子问题而不是两个子问题要被求解。
五元中值组取中值分割法
对于快速排序,枢纽元一种好的选择是选取 3 个元素并取它们的中位数。但它并不提供一种好的保证。为得到一个好的最坏情形,关键想法是再用一个间接层。不是从随机元素的样本中找出中值,而是从一些中值的样本中找出中值。
基本的枢纽元选择算法如下:
- 把 N 个元素分成 ⌊N/5⌋ 组,每组5个元素,忽略剩余的(最多4个)元素。
- 找出每组的中值,得到 ⌊N/5⌋ 个中值的表M。
- 再求出 M 的中值,将其作为枢纽元 v 返回。
使用五元中值组取中值分割法的快速选择算法的运行时间为 O(N)。
整数相乘
设要将两个 N 位数字的数 X 和 Y 相乘,并假设它们都是正的。几乎人在手算时用的算法都需要 O(N2) 次运算,这是因为 X 中的每一位数字都要被 Y 的每一位数字去乘。
如果 X = 61 438 521 而 Y = 94 736 407,那么 XY = 5 820 464 730 934 047。将 X 和 Y 拆成两半,分别由最高几位和最低几位数字组成。此时,XL = 6143,XR = 8521,YL = 9473,YR = 6407。则有 X = XL104 + XR 以及 Y = YL104 +YR,由此得
XY = XLYL108 + (XLYR + XRYL)104 + XRYR。
这个方程由4次乘法组成,即XLYL、XLYR、 XRYL 和 XRYR。它们每一个都是原问题大小的一半(N/2位数字)。若递归地使用该算法进行这4项运算,则得到递归
T(N)=4T(N/2) +O(N)
可知T(N) = O(N2),为得到一个亚二次的算法,必须使用少于4次的递归调用,有
XLYR + XRYL = (XL - XR) (YR - YL) + XLYL +XRYR
此时的递归方程
T(N)=3T(N/2) +O(N)
从而得到 T(N) = O(N1.59)。
相关文章:

【算法设计技巧】分治算法
分治算法 用于设计算法的另一种常用技巧为分治算法(divide and conquer)。分治算法由两部分组成: 分(divide):递归解决较小的问题(当然,基准情况除外)治(conquer):然后,从子问题的解构建原问题的解。 传统上&#x…...

已解决kettle新建作业,点击保存抛出异常Invalid state, the Connection object is closed.
已解决kettle新建作业,点击保存进资源数据库抛出异常Invalid state, the Connection object is closed.的解决方法,亲测有效!!! 文章目录报错问题报错翻译报错原因解决方法联系博主免费帮忙解决报错报错问题 一个小伙伴…...

【设计模式】 工厂模式介绍及C代码实现
【设计模式】 工厂模式介绍及C代码实现 背景 在软件系统中,经常面临着创建对象的工作;由于需求的变化,需要创建的对象的具体类型经常变化。 如何应对这种变化?如何绕过常规的对象创建方法(new),提供一种“封装机制”来…...

深入浅出PaddlePaddle函数——paddle.arange
分类目录:《深入浅出PaddlePaddle函数》总目录 相关文章: 深入浅出TensorFlow2函数——tf.range 深入浅出Pytorch函数——torch.arange 深入浅出PaddlePaddle函数——paddle.arange 语法 paddle.arange(start0, endNone, step1, dtypeNone, nameNone…...

X86 ATT常用寄存器及其操作指令
X86 AT&T常用寄存器及其操作指令 常用寄存器 esp寄存器:当我们需要访问堆栈帧中的变量时,可以使用esp寄存器来获取堆栈帧的基址,以便能够正确地访问堆栈帧中的变量。ebp寄存器:当我们需要调用一个函数时,可以使用…...

Kotlin 高端玩法之DSL
如何在 kotlin 优雅的封装匿名内部类(DSL、高阶函数)匿名内部类在 Java 中是经常用到的一个特性,例如在 Android 开发中的各种 Listener,使用时也很简单,比如://lambda button.setOnClickListener(v -> …...

理光M2701复印机载体初始化方法
理光M2701基本参数: 产品类型:数码复合机 颜色类型:黑白 复印速度:单面:27cpm 双面:16cpm 涵盖功能:复印、打印、扫描 网络功能:支持无线、有线网络打印 接口类型:USB2.0…...
2.25Maven的安装与配置
一.Mavenmaven是一个Java世界中,非常知名的"工程管理工具"/构建工具"核心功能:1.管理依赖在进行一个A 操作之前,要先进行一个B操作.依赖有的时候是很复杂的,而且是嵌套的2.构建/编译(也是在调用jdk)3. 打包把java代码给构建成jar或者warjar就是一个特殊的压缩包…...

《英雄编程体验课》第 12 课 | 递归
文章目录 零、写在前面一、搜索算法的原理二、深度优先搜索三、基于DFS的记忆化搜索四、基于DFS的剪枝五、基于DFS的A*(迭代加深,IDA*)零、写在前面 该章节节选自 《夜深人静写算法》,主要讲解最基础的搜索算法,其中用到的思想就是递归,当然,如果已经对本套体验课了如指…...
35测试不如狗?是你自己技术不够的怨怼罢了
一、做软件测试怎么样? 引用著名软件测试专家、清华大学郑人杰教授的说法:软件测试工程师是一个越老越吃香的职业。 其中就表达了软件测试工作相对稳定、对年龄没有限制、而且随着项目经验的不断增长和对行业背景的深入了解,会越老越吃香。…...

【代码训练营】day42 | 1049. 最后一块石头的重量 II 494. 目标和 474.一和零
所用代码 java 最后一块石头的重量II LeetCode 1049 题目链接:最后一块石头的重量II LeetCode 1049 - 中等 思路 无。 把石头分成重量总和近似两堆,然后两堆石头相撞,剩下的就是最小的石头。每个石头只能用一次,01背包…...

Golang协程常见面试题
协程面试题交替打印奇数和偶数N个协程打印1到maxVal交替打印字符和数字交替打印字符串三个协程打印ABCChannel练习交替打印奇数和偶数 下面让我们一起来看看golang当中常见的算法面试题 使用两个goroutine交替打印1-100之间的奇数和偶数, 输出时按照从小到大输出. 方法一&…...
)
种群多样性:智能优化算法求解基准测试函数F1-F23种群动态变化图(视频)
智能优化算法求解基准测试函数F1种群动态变化图智能优化算法求解基准测试函数F2种群动态变化图智能优化算法求解基准测试函数F3种群动态变化图智能优化算法求解基准测试函数F4种群动态变化图智能优化算法求解基准测试函数F5种群动态变化图智能优化算法求解基准测试函数F6种群动…...
Qt 中的XML
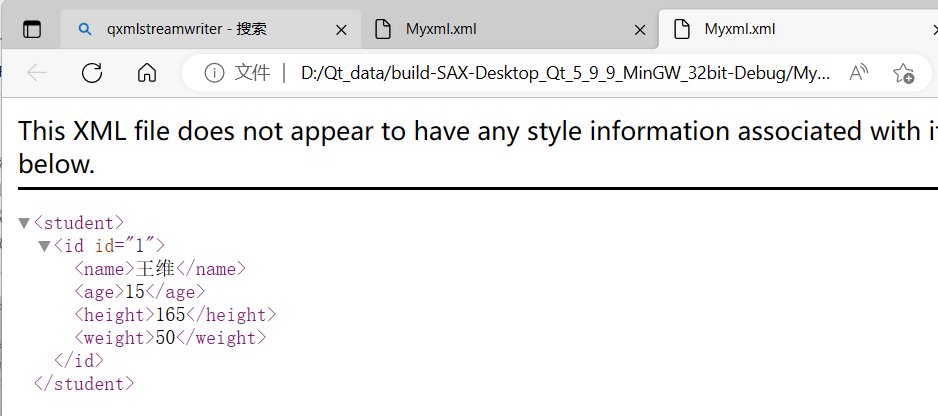
XML的基本介绍: 在前端开发中:HTML是用来显示数据,而XML是用来传输和存储数据的 XML 指可扩展标记语言(EXtensible Markup Language)XML 是一种标记语言,很类似 HTMLXML 的设计宗旨是传输数据,而…...
网络应用之URL
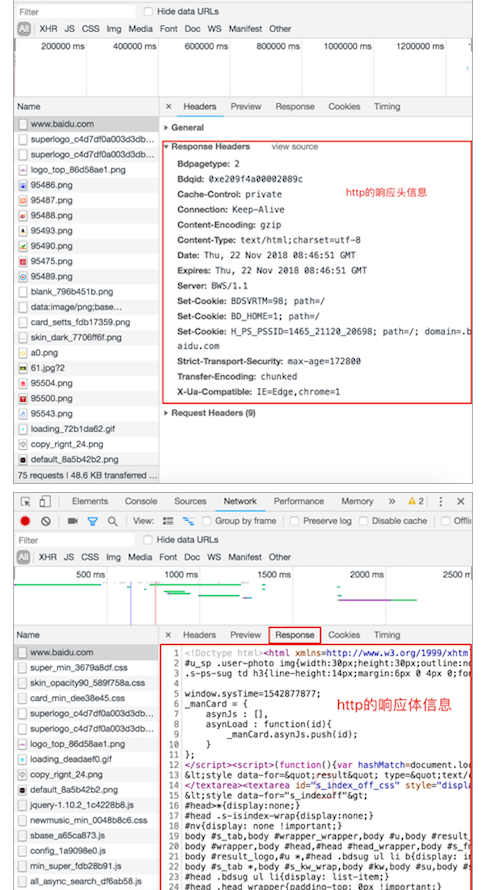
URL学习目标能够知道URL的组成部分1. URL的概念URL的英文全拼是(Uniform Resoure Locator),表达的意思是统一资源定位符,通俗理解就是网络资源地址,也就是我们常说的网址。2. URL的组成URL的样子:https://news.163.com/18/1122/10/E178J2O4000189FH.html…...
【Linux】重定向原理dup2缓冲区
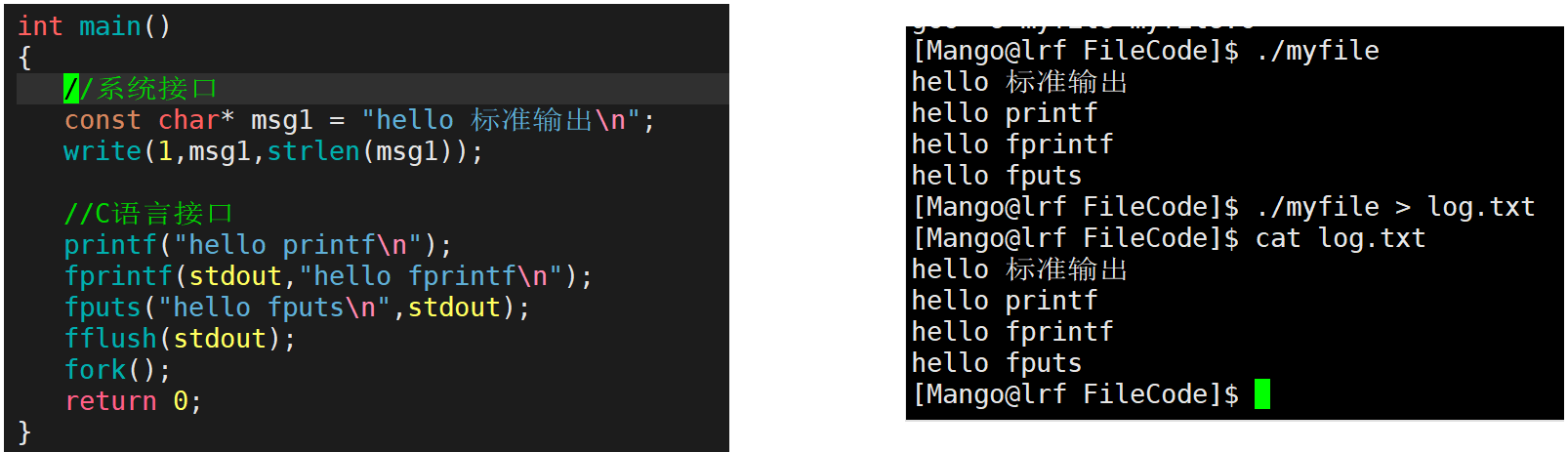
文章目录重定向原理输出重定向关于FILE解释输出重定向原理追加重定向输入重定向dup2缓冲区语言级别的缓冲区内核缓冲区重定向原理 重定向的本质就是修改文件描述符下标对应的struct file*的内容 输出重定向 输出重定向就是把本来应该输出到显示器的数据重定向输出到另一个文…...

ROG配置ubuntu20.04.5双系统要点
win11ubuntu20.04.5 1. BIOS设置 开机长按F2进入bios设置,修改advanced参数: boot -> 关闭fast bootsecurity -> 关闭secure boot设置VMD controller为Disabled(其他电脑是修改硬盘的SATA和ACHI模式)。但是改了之后windo…...

机械革命旷世G16电脑开机变成绿屏了无法使用怎么办?
机械革命旷世G16电脑开机变成绿屏了无法使用怎么办?最近有用户使用的机械革命旷世G16电脑一开机之后,电脑屏幕就变成了绿色的,无法进行任何的操作。出现这个问题可能是因为电脑中病毒了,或者是系统出现故障。我们可以通过U盘来重新…...

python中关于time模块的讲解---指定格式时间字符串转为时间戳
本文章可以解决任意字符串格式时间转为时间戳 返回json格式 可以在此基础上进行修改 时间格式控制符 说明 %Y 四位数的年份,取值范围为0001~9999,如1900 %m 月份(01~12),例如10 %d 月中的一天(01~31)例…...

MySql存储引擎与索引
MySql引擎 存储引擎是具体操作数据的地方,是一种对数据存储的技术与其配套的功能 不同存储引擎所采用存储的方式的不同,并且索引技巧与锁定水平也不同 根据业务的需求灵活的选择存储引擎即可满足的实际的需要 Innodb Innodb是MySql中的默认安装的引擎…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
