力扣100097. 合法分组的最少组数(哈希+贪心)
题目描述:
给你一个长度为 n 下标从 0 开始的整数数组 nums 。
我们想将下标进行分组,使得 [0, n - 1] 内所有下标 i 都 恰好 被分到其中一组。
如果以下条件成立,我们说这个分组方案是合法的:
- 对于每个组
g,同一组内所有下标在nums中对应的数值都相等。 - 对于任意两个组
g1和g2,两个组中 下标数量 的 差值不超过1。
请你返回一个整数,表示得到一个合法分组方案的 最少 组数。
示例 1:
输入:nums = [3,2,3,2,3] 输出:2 解释:一个得到 2 个分组的方案如下,中括号内的数字都是下标: 组 1 -> [0,2,4] 组 2 -> [1,3] 所有下标都只属于一个组。 组 1 中,nums[0] == nums[2] == nums[4] ,所有下标对应的数值都相等。 组 2 中,nums[1] == nums[3] ,所有下标对应的数值都相等。 组 1 中下标数目为 3 ,组 2 中下标数目为 2 。 两者之差不超过 1 。 无法得到一个小于 2 组的答案,因为如果只有 1 组,组内所有下标对应的数值都要相等。 所以答案为 2 。
示例 2:
输入:nums = [10,10,10,3,1,1] 输出:4 解释:一个得到 2 个分组的方案如下,中括号内的数字都是下标: 组 1 -> [0] 组 2 -> [1,2] 组 3 -> [3] 组 4 -> [4,5] 分组方案满足题目要求的两个条件。 无法得到一个小于 4 组的答案。 所以答案为 4 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 109
思路:
题目要求我们求出最小的分组数目,首先我们可以确定的是,一个数组一定有答案,因为再不济把他每个元素都分一个组就可以了,又由于对于任意两个组 g1 和 g2 ,两个组中 下标数量 的 差值不超过1,假设我们分的所有的组的下标数量最小为k,那么最大也只能是k+1.
我们可以先用一个map存下每一个数出现的次数,对于每一个数it,出现的次数为cnt,我们看能否将这cnt个it分为只包含k个和k+1个的组。
假设数组中出现的最小次数的数目为mi,那么很容易得到k<=mi.如果k>mi,意味着至少有一组凑不够k个相同的数(同一组内所有下标在 nums 中对应的数值),所以我们可以遍历k(分的所有的组的下标数量最小值),k确定了,k+1也就确定了。
对于每一个k,我们看nums里的所有数出现的次数能不能分为只包含k个和k+1个的组。
如果可以,我们就把当前k可以分得的最小组的数目求一个最小值ans.
如果不能那就。。。那就不能。
时间复杂读为什么是O(n)?
假设t表示的是nums数组中不同元素的个数,那么最小出现次数mi<=n/t,所以mi*t<=n.
O(min(mp[nums[i])*t)=O(mi*t)=O(n/t *t)=O(n)
这里计算时间复杂度非常重要哦,我开始也是算错了时间复杂度以为是o(n^2)了。、
代码:
class Solution {
public:int minGroupsForValidAssignment(vector<int>& nums) {map<int,int> mp;int len=nums.size();int mi=1e9+10;//最少出现次数for(auto it:nums){mp[it]++;//记录每个元素出现的次数}for(auto it:mp){mi=min(it.second,mi);}int ans=1e9;for(int k=1;k<=mi;k++){int tn=0;//记录当前k可以分得到的最小数目的组数int f=1;for(auto it:mp){int cnt=it.second;int a = cnt / (k + 1);int b = cnt - a * (k + 1);if (cnt % (k + 1) == 0) {//尽量拼元素多的组tn += a;}else if (a + b >= k){//看能不能在a个(k+1)的组里面分诺干个1到剩下的b里面tn += a + 1;}else{//优先拼k+1组失败了,退而求其次优先考虑拼k组int a = cnt / (k );int b = cnt - a * (k);if(b>a){//如果剩下的元素b不能分到a个(k)组里面,说明分组失败f=0;break;}tn+=a;}}if(f) ans=min(ans,tn);}return ans;}
};相关文章:
)
力扣100097. 合法分组的最少组数(哈希+贪心)
题目描述: 给你一个长度为 n 下标从 0 开始的整数数组 nums 。 我们想将下标进行分组,使得 [0, n - 1] 内所有下标 i 都 恰好 被分到其中一组。 如果以下条件成立,我们说这个分组方案是合法的: 对于每个组 g ,同一…...
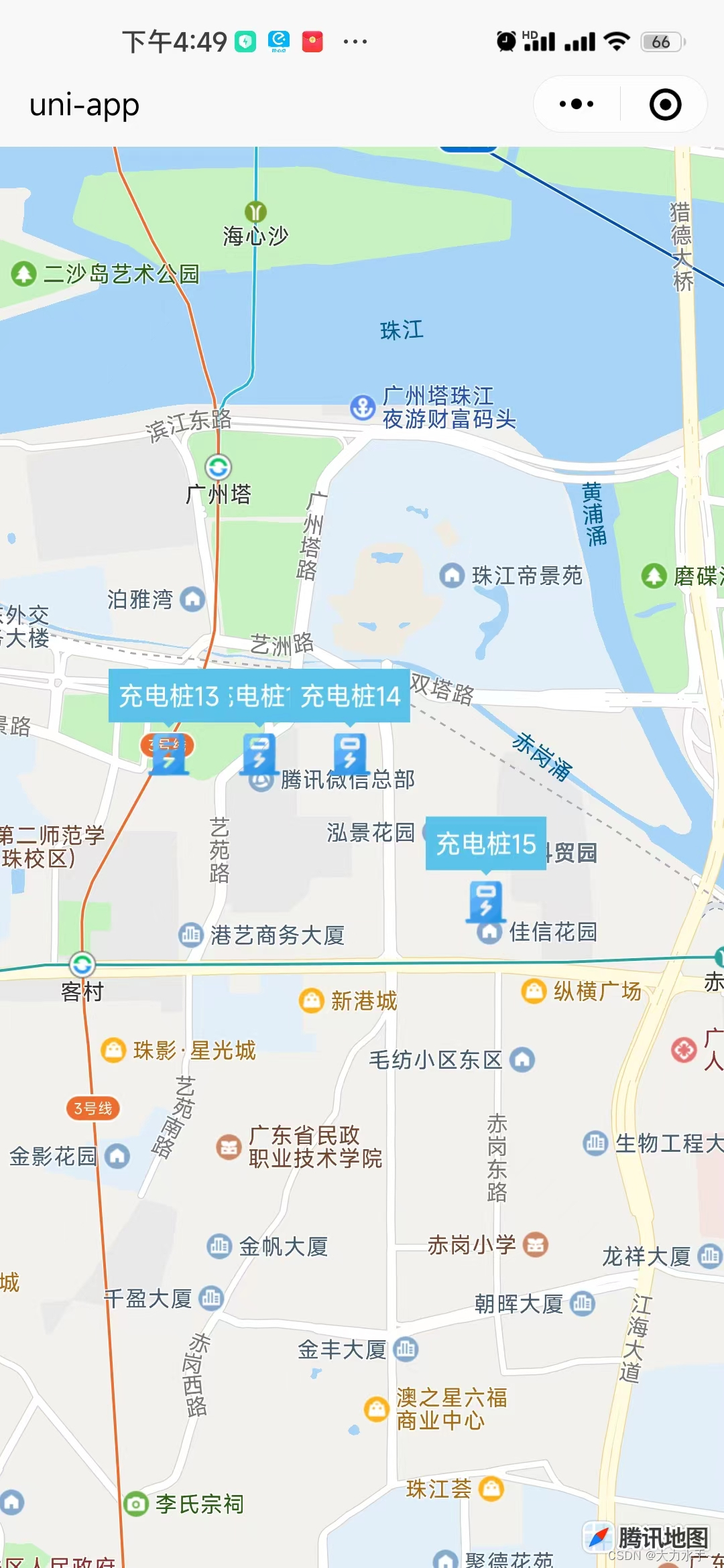
uniapp map地图实现marker聚合点,并点击marker触发事件
1.uniapp官方文档说明 2.关键代码片段 // 仅调用初始化,才会触发 on.("markerClusterCreate", (e) > {})this._mapContext.initMarkerCluster({enableDefaultStyle: false, // 是否使用默认样式zoomOnClick: true, // 点击聚合的点,是否…...
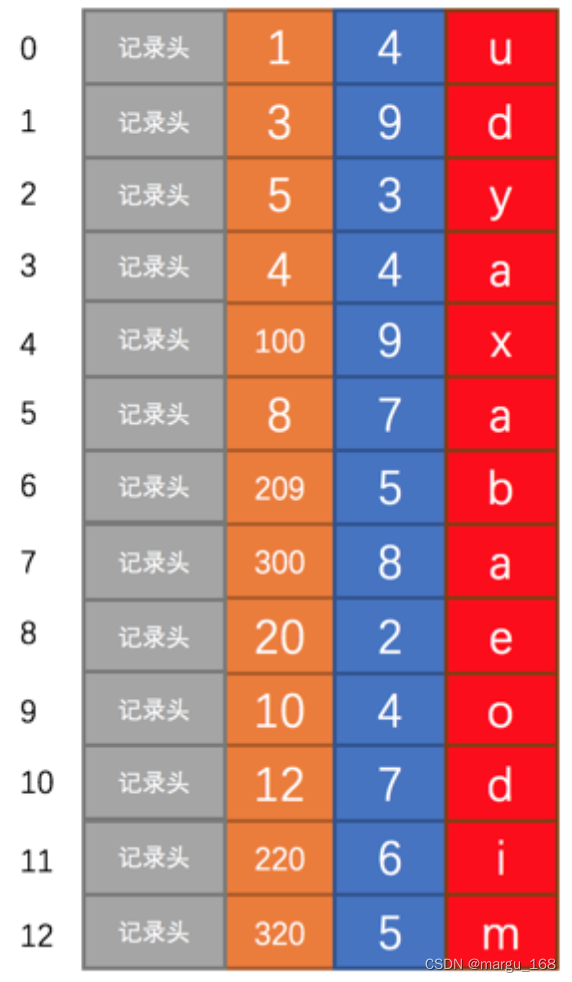
【Mysql】Mysql中的B+树索引(六)
概述 从上一章节我们了解到InnoDB 的数据页都是由7个部分组成,然后各个数据页之间可以组成一个双向链表 ,而每个数据页中的记录会按照主键值从小到大的顺序组成一个单向链表 ,每个数据页都会为存储在它里边儿的记录生成一个页目录 ÿ…...
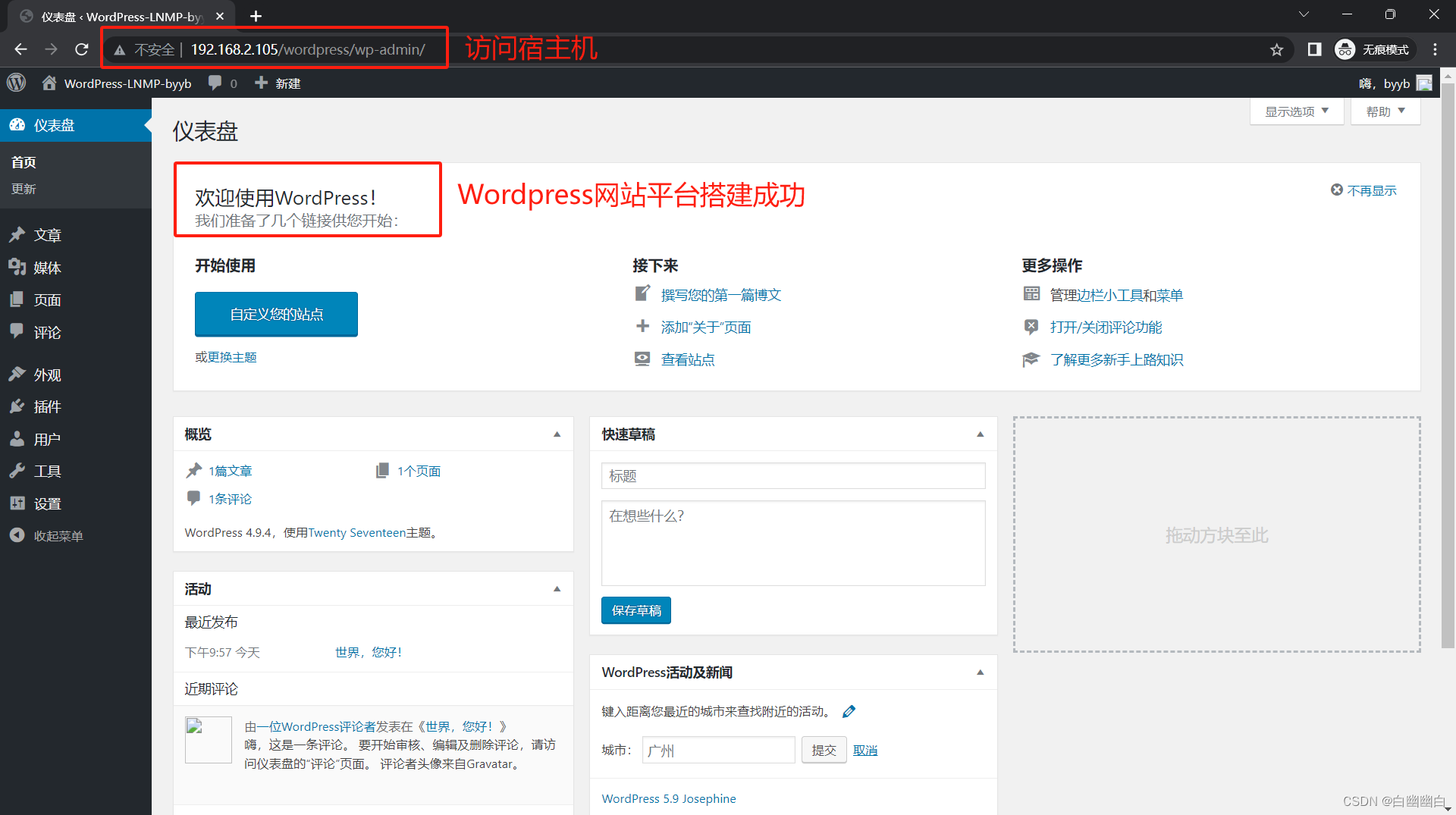
【Dockerfile镜像实战】构建LNMP环境并运行Wordpress网站平台
这里写目录标题 一、项目背景和要求二、项目环境三、部署过程1)创建自定义网络2)部署NginxStep1 创建工作目录并上传相关软件包Step2 编写Dockerfile文件Step3 编写配置文件nginx.confStep4 创建nginx镜像Step5 运行容器 3)部署MysqlStep1 创…...

【工具】利用ffmpeg将网页中的.m3u8视频文件转化为.mp4格式
目录 0.环境 1.背景 2.前提 3.详细描述 1)在网站上找到你想下载的视频的.m3u8链接 2)打开命令行,用ffmpeg命令进行转化 3)过程&结果截图 0.环境 windows64 ffmpeg 1.背景 网页上有个.m3u8格式的视频文件,…...

Git简洁安装方式和使用方式【附安装包资源,Git基础操作,如拉取项目、上传代码、拉取代码】
文章目录 软件安装包安装步骤常用使用方式注意拉取项目上传代码或文件选择文件添加到本地Git存储库的缓存区将缓存区的更改提交到本地Git存储库,并设置提交信息将本地Git存储库的更新推送到远程Git仓库中上传示例拉取别人所上传的代码 常见问题上传代码失败…...
【29】c++设计模式——>策略模式
策略模式 C中的策略模式(Strategy Pattern)是一种行为型设计模式,它允许在运行时选择算法的行为。策略模式通过将算法封装成独立的类,并且使它们可以互相替换,从而使得算法的变化独立于使用算法的客户端。 策略模式通…...
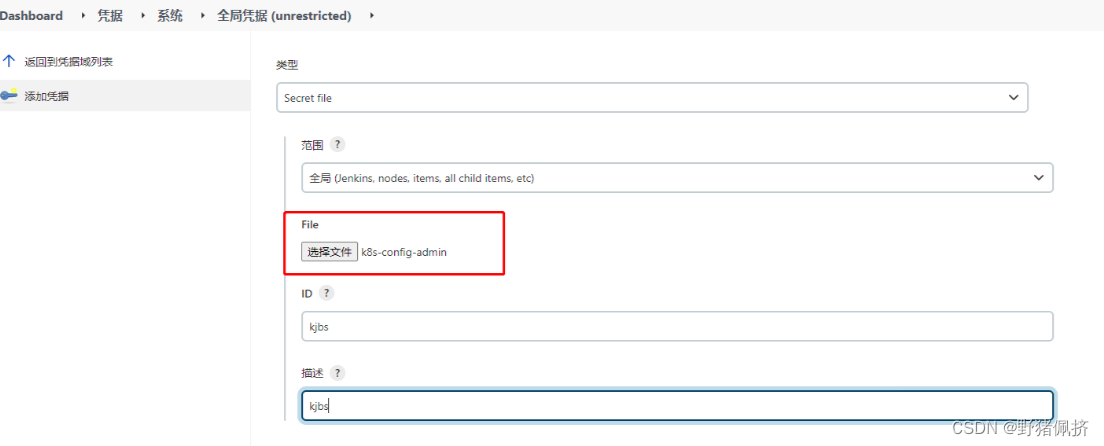
2023Jenkins连接k8s
首先配置k8s config文件 1.方式获取k8s密钥 cat .kube/config 2.导出方式或者密钥 kubectl config view --raw > k8s-config-admin pipeline {agent {kubernetes {yaml apiVersion: v1kind: Podmetadata:labels:some-label: devopsspec:containers:- name: dockerimage: d…...
SpringBoot 入门 参数接收 必传参数 数组 集合 时间接收
接口声明 RestController //表示该类为请求处理类public class HttpDeal {RequestMapping("/login")//这个方法处理哪一个地址过来的请求public String hello(){return "返回给浏览器";}}接收参数 RequestMapping("/login")public String logi…...

【Qt之JSON文件】QJsonDocument、QJsonObject、QJsonArray等类介绍及使用
Qt之JSON相关类介绍 QJsonDocument常用函数枚举类型 QJsonDocument::DataValidation枚举类型 QJsonDocument::JsonFormat构造函数静态函数成员函数示例 QJsonObject常用函数构造函数:成员函数: QJsonObject 与 QVariantMap 相互转换 QJsonArray常用函数构…...

阿里云今年有双十一活动吗?不好说
阿里云今年有双十一活动吗?不好说,因为去年就没有。阿里云双11优惠活动是一项大型的促销活动,每年都有,但是去年没有双十一活动,不知道今年2023年阿里云是否有双11优惠活动。但是阿里云百科aliyunbaike.com猜想&#x…...

【驱动开发】创建设备节点、ioctl函数的使用
一、控制三盏灯的亮灭 头文件: #ifndef __HEAD_H__ #define __HEAD_H__ typedef struct{unsigned int MODER;unsigned int OTYPER;unsigned int OSPEEDR;unsigned int PUPDR;unsigned int IDR;unsigned int ODR; }gpio_t; #define PHY_LED1_ADDR 0X50006000 #def…...
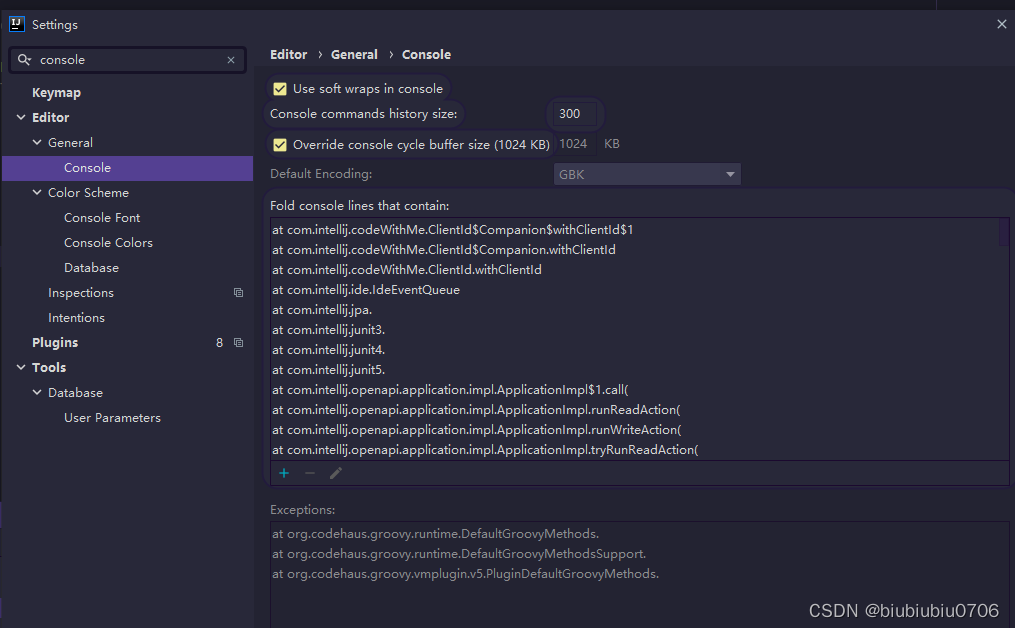
Tomcat启动控制台乱码问题
修改Tomcat/conf/logging.properties...

学习周总结
http://t.csdnimg.cn/DKki2 http://t.csdnimg.cn/NvudJ 项目进度 做了大概的主界面,然后做了一个客户端和服务端的分离,实现了在客户端发送的信息,在服务端能收到;客户端和服务端的制作是我之前有写的一个http://t.csdnimg.cn/…...

如何在不恢复出厂设置的情况下解锁 Android 手机密码?
当您忘记 Android 手机的密码时,可能会有压力,尤其是当您不想恢复出厂设置并删除所有数据时。但是,有一些方法可以在不诉诸如此激烈的步骤的情况下解锁手机。我们将在这篇文章中教您如何在不恢复出厂设置的情况下解锁 Android 手机密码。我们…...

移动设备管理对企业IT 安全的增强
移动设备管理 (MDM) 是通过定义策略和部署安全控制(如移动应用程序管理、移动内容管理和条件 Exchange 访问)来管理移动设备的过程。 完整的MDM解决方案可以管理在Android,iOS,Windows,macOS&a…...

app分发的一些流程
应用分发的流程通常包括以下步骤: 开发应用程序:首先,您需要开发您的应用程序。这包括编写代码、设计用户界面、测试应用程序等等。确保您的应用程序符合各个应用商店的规范和要求,以确保顺利通过审核。 准备应用材料:…...

深入浅出讲解Spring IOC和DI的区别
Spring IOC和DI的区别 一,介绍 前言 很多人都会把ioc和di说成同一个东西,其实IOC和DI虽然在概念上可以笼统地视为同一事物,但其本质上存在区别。IOC(Inverse of Control,控制反转)从容器的角度描述&#…...

文件操作 IO
文件(File) 狭义的文件: 指的是硬盘上的文件和目录 广义的文件: 泛指计算机中很多软硬件资源(操作系统中把很多硬件和软件资源抽象成了文件, 按照文件的方式同意管理) 本章内容只讨论狭义的文件 路径 绝对路径: 以c: , d: 盘符开头的路径相对路径: 以当前所在的目录为基准(…...

ARouter - 组件化通信方案
官网 https://github.com/alibaba/ARouter/blob/master/README_CN.md 项目简介 一个用于帮助 Android App 进行组件化改造的框架 —— 支持模块间的路由、通信、解耦 功能介绍 支持直接解析标准URL进行跳转,并自动注入参数到目标页面中支持多模块工程使用支持添…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...
