用matlab求解线性规划
文章目录
- 1、用单纯形表求解线性规划
- 绘制单纯形表求解:
- 2、用matlab求解线性规划——linprog()函数
- 问题:
- 补充代码:显示出完整的影子价格向量
1、用单纯形表求解线性规划
求解线性规划 m i n − 3 x 1 − 4 x 2 + x 3 min -3x_1-4x_2+x_3 min−3x1−4x2+x3,
约束条件为
2 x 1 + 3 x 2 ≤ 12 2x_1+3x_2≤12 2x1+3x2≤12
5 x 1 + x 2 + x 3 = 19 5x_1+x_2+x_3=19 5x1+x2+x3=19,
x 1 , x 2 , x 3 ≥ 0 x_1,x_2,x_3≥0 x1,x2,x3≥0.
绘制单纯形表求解:
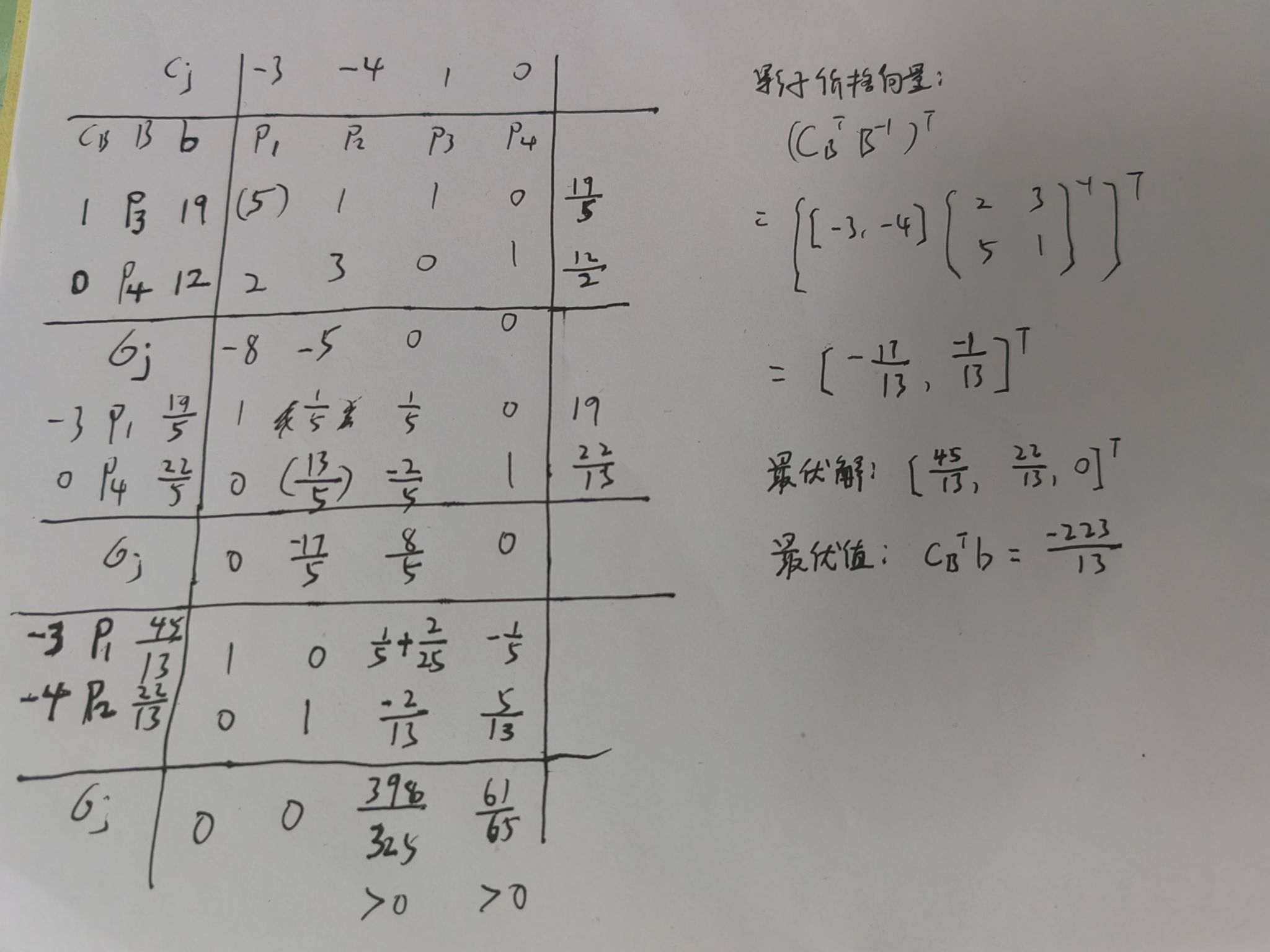
2、用matlab求解线性规划——linprog()函数

clc,clear,close all;
% 定义目标函数的系数向量
f = [-3; -4; 1];% 定义不等式约束的系数矩阵和右侧常数向量
A = [2, 3, 0];
b = [12];% 定义等式约束的系数矩阵和右侧常数向量
Aeq = [5, 1, 1];
beq = [19];% 定义变量的边界
lb = zeros(3, 1); % 所有变量的下界都是0% 使用linprog求解线性规划问题
[x, fval, exitflag, output, lambda] = linprog(f, A, b, Aeq, beq, lb);% 输出结果
fprintf('最小值为: %.4f\n', fval);
fprintf('x1 = %.4f, x2 = %.4f, x3 = %.4f\n', x(1), x(2), x(3));fprintf('\n')
disp('输出结果(以分数形式显示):')
fprintf('最小值为: %s\n', rats(fval));
fprintf('x1 =%s, x2 =%s, x3 =%s\n', rats(x(1)), rats(x(2)), rats(x(3)));% 输出影子价格向量(以分数形式显示)
fprintf('影子价格向量为:\n');
disp(rats(lambda.ineqlin));
返回结果:
Optimal solution found.最小值为: -17.1538
x1 = 3.4615, x2 = 1.6923, x3 = 0.0000输出结果(以分数形式显示):
最小值为: -223/13
x1 = 45/13 , x2 = 22/13 , x3 = 0
影子价格向量为:17/13
问题:
此处发现两个问题,主要体现在影子价格向量上:
1、影子价格少一个元素
2、影子价格向量元素和用代数公式法求解的结果差一个负号
通过查阅Mathworks官方文档,可以看到缺少负号并不是程序编写错误问题:

补充代码:显示出完整的影子价格向量
问题1的解决方法:需要将约束条件中的不等式全部写为等式。
因为将一个不等式和一个等式的约束条件传递给linprog函数时,它会计算一个相对较小的影子价格向量,其中包含了不等式约束的影响,而等式约束的影响通常不单独表示在影子价格向量中。
%% 约束条件全部为等式
disp('求解完整的影子价格向量:')
% 定义目标函数的系数向量
f = [-3; -4; 1];% 定义不等式约束的系数矩阵和右侧常数向量
A = [2, 3, 0; 5, 1, 1];
b = [12; 19];% 定义变量的边界
lb = zeros(3, 1); % 所有变量的下界都是0% 使用linprog求解线性规划问题
[x, fval, exitflag, output, lambda] = linprog(f, A, b, [], [], lb);% 输出结果
fprintf('最小值为: %.4f\n', fval);
fprintf('x1 = %.4f, x2 = %.4f, x3 = %.4f\n', x(1), x(2), x(3));% 输出影子价格向量
fprintf('影子价格向量为:\n');
disp(lambda.ineqlin);fprintf('\n')
disp('输出结果(以分数形式显示):')
fprintf('最小值为: %s\n', rats(fval));
fprintf('x1 =%s, x2 =%s, x3 =%s\n', rats(x(1)), rats(x(2)), rats(x(3)));% 输出影子价格向量(以分数形式显示)
fprintf('影子价格向量为:\n');
disp(rats(lambda.ineqlin));
fprintf('\n')
返回结果:
求解完整的影子价格向量:Optimal solution found.最小值为: -17.1538
x1 = 3.4615, x2 = 1.6923, x3 = 0.0000
影子价格向量为:1.30770.0769输出结果(以分数形式显示):
最小值为: -223/13
x1 = 45/13 , x2 = 22/13 , x3 = 0
影子价格向量为:17/13 1/13
相关文章:

用matlab求解线性规划
文章目录 1、用单纯形表求解线性规划绘制单纯形表求解: 2、用matlab求解线性规划——linprog()函数问题:补充代码:显示出完整的影子价格向量 1、用单纯形表求解线性规划 求解线性规划 m i n − 3 x 1 − 4 x 2 x 3 min -3x_1-4x_2x_3 min−…...
)
antd获取/更改form表单数据(表单域数据)
创建ref引用 formRef React.createRef();表单和ref绑定 //ref{this.formRef} 先给Form <Form ref{this.formRef} name"control-ref" onFinish{this.onFinish}><Form.Item name"name" label"Name" rules{[{ required: true }]}>…...

Go学习第三章——运算符与进制
Go学习第三章——运算符与进制 1 算术运算符2 关系运算符3 逻辑运算符4 赋值运算符5 其他运算符5.1 位运算符5.2 跟指针有关的运算符 6 运算符的优先级7 获取用户终端输入8 进制转换8.1 进制基本使用8.2 进制之间的转换8.3 原码 反码 补码8.4 位运算符详解 运算符是—种特殊的符…...
H3C IMC dynamiccontent.properties.xhtm 远程命令执行
我举手向苍穹,并非一定要摘星取月,我只是需要这个向上的、永不臣服的姿态。 构造payload: /imc/javax.faces.resource/dynamiccontent.properties.xhtml pfdrtsc&lnprimefaces&pfdriduMKljPgnOTVxmOB%2BH6%2FQEPW9ghJMGL3PRdkfmbii…...
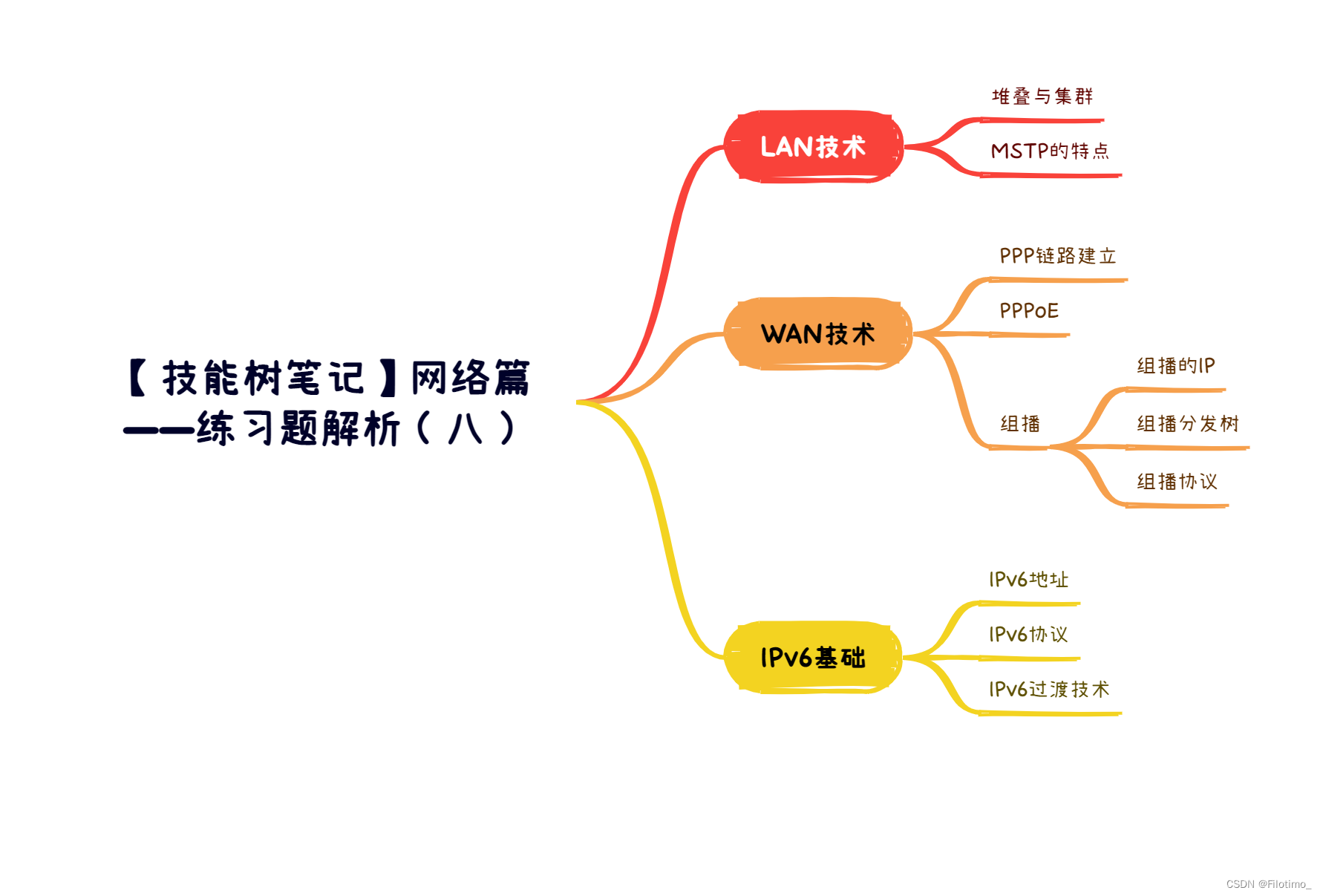
【技能树笔记】网络篇——练习题解析(八)
目录 前言 一、LAN技术 1.1 堆叠与集群 1.2 MSTP的特点 二、WAN技术 2.1 PPP链路建立 2.2 PPPoE 2.3 组播 2.3.1 组播的IP 2.3.2 组播分发树 2.3.3 组播协议 三、IPv6基础 3.1 IPv6地址 3.2 IPv6协议 3.3 IPv6过渡技术 总结 🌈嗨!我是Filotimo__…...
)
laravel框架介绍(二)
方法1.windows 可以直接下载 Composer-Setup.exe 方法2.配置php.exe目录环境变量,下载 composer.phar和php.exe平级目录, 新建 composer.bat 文件编辑以下内容 php "%~dp0composer.phar" %* 运行composer.bat ,出现版本号为成功 执行 composer self-update 以保持 Co…...

USB学习(1):USB基础之接口类型、协议标准、引脚分布、架构、时序和数据格式
连接计算机外围设备最简单的方法是通过USB(通用串行总线)。USB是即插即用接口,可以将扫描仪、打印机、数码相机、闪存驱动器等计算机外围设备连接到计算机上。本篇文章就来介绍一下USB的一些基础知识,包括。 文章目录 1 接口类型和标准规范2 引脚分布3 …...

less和scss语法详解
比较好的博客文章:Less使用语法(详细):https://blog.csdn.net/weixin_44646763/article/details/114193426 SCSS基本语法:https://www.jianshu.com/p/4efaac23cdb6 总结:我理解的点: 1、符号声…...
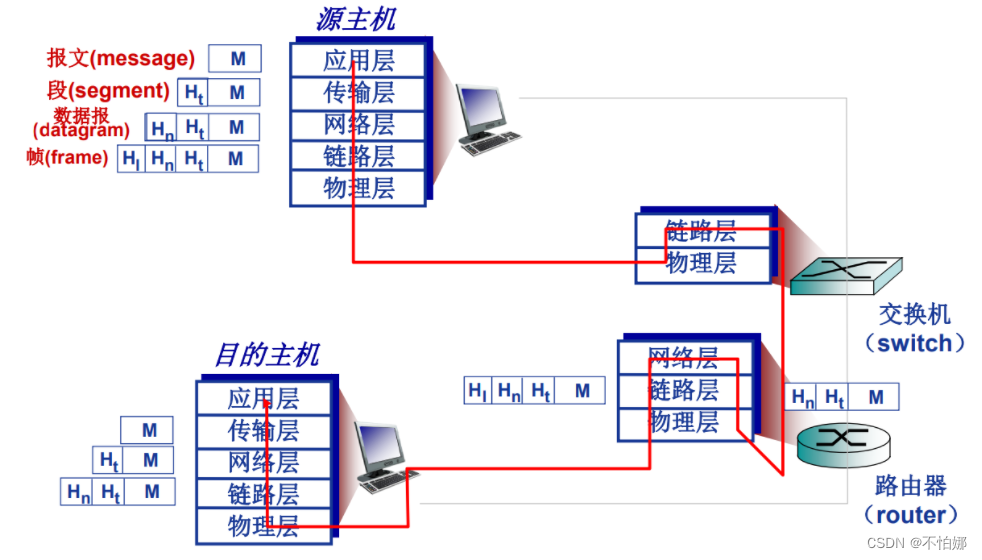
【计算机网络笔记】TCP/IP参考模型基本概念,包括五层参考模型
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...

RSA加密与签名的区别
文章目录 一、签名验签原理二 RSAUtils 工具类三、通过x509Certificate来获取CA证书的基本信息四、 通过公钥获取公钥长度 一、签名验签原理 签名的本质其实就是加密,但是由于签名无需还原成明文,因此可以在加密前进行哈希处理。所以签名其实就是哈希加…...

arcgis js api 4.x通过TileLayer类加载arcgis server10.2发布的切片服务跨域问题的解决办法
1.错误复现 2.解决办法 2.1去https://github.com/Esri/resource-proxy 网站下载代理配置文件,我下载的是最新的1.1.2版本,这里根据后台服务器配置情况不同有三种配置文件,此次我用到的是DotNet和Java. 2.2 DotNet配置 2.2.1 对proxy文件增加…...

如何让chatGPT给出高质量的回答?
如何让chatGPT给出高质量的回答? ChatGPT从入门到进阶教程合集_哔哩哔哩_bilibili 公式 【指令词】【背景】【输入】【输出要求】 1. 指令词 ——精准任务or命令 如:简述、解释、翻译、总结、润色 2. 背景 ——补充信息 如:简述一篇讲解…...
-- idea(2022版)将commit(未push)的 本地仓库 的 单条commit记录 进行撤销)
Java后端开发(八)-- idea(2022版)将commit(未push)的 本地仓库 的 单条commit记录 进行撤销
目录 1.修改Test01类后,提交到本地仓库 。 2.commit成功后,在Git =》Log中会显示,commit记录...

Mysql架构解析,InnoDB架构概述。
MySQL架构解析 Mysql整体架构 MySQL整体架构如下图所示: MySQL逻辑系统架构分为4层: 应用层MySQL服务层存储引擎层系统文件层 下面将对各层的功能和组件进行介绍,并探讨一条语句的执行过程。 应用层 应用层是MySQL体系架构的最上层,它…...
jmeter如何测试websocket接口?
jmeter做接口测试,很多人都是做http协议的接口,就有很多人问websocket的接口怎么测试啊? 首先,我们要明白,websocket接口是什么接口。 然后,我们怎么用jmeter测试? jmeter要测试websocket接口…...
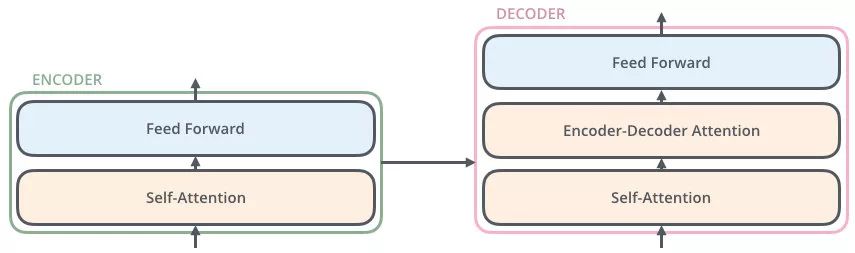
15 Transformer 框架概述
整体框架 机器翻译流程(Transformer) 通过机器翻译来做解释 给一个输入,给出一个输出(输出是输入的翻译的结果) “我是一个学生” --》(通过 Transformer) I am a student 流程 1 编码器和解…...
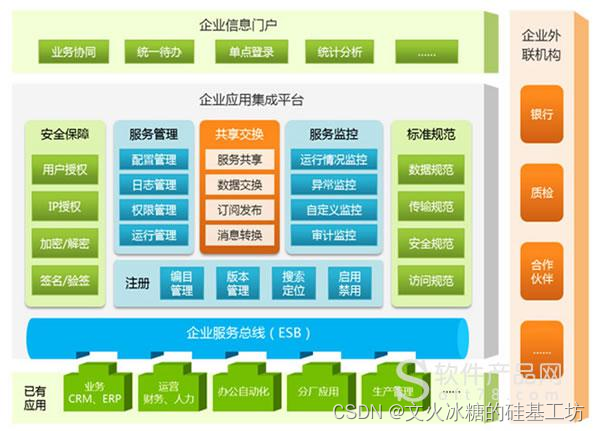
[架构之路-241]:目标系统 - 纵向分层 - 企业信息化与企业信息系统(多台企业应用单机组成的企业信息网络)
目录 前言: 一、什么是信息系统:计算机软件硬件系统 1.1 什么是信息 1.2 什么是信息系统 1.3 什么是信息技术 1.4 什么是信息化与信息化转型 1.5 什么是数字化与数字化转型(信息化的前提) 1.6 数字化与信息化的比较 1.7 …...

flink中使用异步函数的几个注意事项
背景 在flink系统中,我们为了补充某个流事件成一个完整的记录,经常需要调用外部接口获取一些配置数据,流事件结合这些配置数据就可以组合成一条完整的记录,然而如果同步调用外部系统接口来实现,那么会有很大的性能瓶颈…...

QML之Repeater 控件使用
Repeater 控件是 重复作用 根据 model中的index 数量进行重复 废话不说 直接看如何用 当model 为数字时 Rectangle{height: 1200width: 500visible: trueanchors.fill: parentColumn{spacing: 20Repeater{model: 10delegate: Rectangle{width: 60height: 20color: index%2 …...

哈希树讲解
哈希树(HashTree)是哈希(Hash)算法的一种延续。传统数据结构中对如何避免哈希冲突都有一定的描述和解释,但是这些描述和解释都是泛泛而谈,并没有提出比较好的解决方案。这里所提到的哈希树(HashTree)算法就是要提供一种在理论上和实际应用中均能有效地处…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
