LeetCode:1402. 做菜顺序、2316. 统计无向图中无法互相到达点对数
1. 1402 做菜顺序
题目详细为:
一个厨师收集了他 n 道菜的满意程度 satisfaction ,这个厨师做出每道菜的时间都是 1 单位时间。
一道菜的 「 like-time 系数 」定义为烹饪这道菜结束的时间(包含之前每道菜所花费的时间)乘以这道菜的满意程度,也就是 time[i]*satisfaction[i] 。
返回厨师在准备了一定数量的菜肴后可以获得的最大 like-time 系数 总和。
你可以按 任意 顺序安排做菜的顺序,你也可以选择放弃做某些菜来获得更大的总和。
示例为:
示例 1:
输入:satisfaction = [-1,-8,0,5,-9]
输出:14
解释:去掉第二道和最后一道菜,最大的 like-time 系数和为 (-11 + 02 + 53 = 14) 。每道菜都需要花费 1 单位时间完成。
示例 2:
输入:satisfaction = [4,3,2]
输出:20
解释:可以按照任意顺序做菜 (21 + 32 + 43 = 20)
示例 3:
输入:satisfaction = [-1,-4,-5]
输出:0
解释:大家都不喜欢这些菜,所以不做任何菜就可以获得最大的 like-time 系数。
提示:
n == satisfaction.length
1 <= n <= 500
-1000 <= satisfaction[i] <= 1000
难度:【困难】
算法思路:
由于n的取值并没有很大,所以使用暴力解法解决这题完全没有问题,但是个人觉得可以这样来实现。
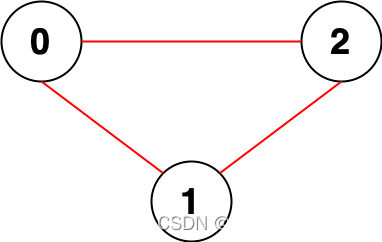
可以分为三类情况,(1)satisfaction这个数组(列表)中的最大数小于零,这样得到最终结果(按照上述公式)肯定小于0,那么直接返回0即可;(2)satisfaction这个数组(列表)中的最小数大于零,对这个数组进行升序排序,然后利用上述公式计算返回即可;(3)satisfaction这个数组(列表)中同时存在小于0和大于0的数,首先对这个数组进行升序排序,然后用一个变量根据上述公式计算对应结果num2,用变量num存储数组的和,之后再遍历这个数组,变量ans(初始值为0)返回最终结果,执行下述操作即可,ans = max(ans,num2),num2 -= num,num -= satisfaction[i],示意图如下:
satisfaction数组
排序前 [-1,-8,0,5,-9]
排序后 [-9,-8,-1,0,5]
num的值为:-13
num2的值为:-9 * 1 + -8 * 2 + -1 * 3 + 0 * 4 + 5 * 5 = -3
ans = 0
遍历次数 ans num num2
1 0 -13 -3
2 0 -4 10
3 10 4 14
4 14 5 10
5 14 5 5
参考代码如下:
class Solution(object):def maxSatisfaction(self, satisfaction):""":type satisfaction: List[int]:rtype: int"""satisfaction.sort()if satisfaction[-1] < 0:return 0ans = 0n = len(satisfaction)if satisfaction[0] > 0:start = 1for e in satisfaction:ans += start * estart += 1else:num = sum(satisfaction)num2 = 0for i in range(n):num2 += satisfaction[i] * (i+1)for i in range(n):ans = max(ans,num2)num2 -= numnum -= satisfaction[i]return ansa = Solution()
print(a.maxSatisfaction(satisfaction = [-1,-8,0,5,-9]))运行结果:
虽然算法效率总体还不怎么的,但是比暴力肯定要好一些。
2. 2316. 统计无向图中无法互相到达点对数
题目详细为:
给你一个整数 n ,表示一张 无向图 中有 n 个节点,编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。
请你返回 无法互相到达 的不同 点对数目 。
示例为:
输入:n = 3, edges = [[0,1],[0,2],[1,2]]
输出:0
解释:所有点都能互相到达,意味着没有点对无法互相到达,所以我们返回 0 。
2.
输入:n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出:14
解释:总共有 14 个点对互相无法到达:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。
提示:
提示:
1 <= n <= 105
0 <= edges.length <= 2 * 105
edges[i].length == 2
0 <= ai, bi < n
ai != bi
不会有重复边。
算法思路:
从0号节点依次遍历到n-1号节点,如果遍历到某节点时,在map中已经存在了,那么不需要再进行接下来的操作,否则,在map中记录当前节点,然后依次遍历与该节点连通的节点,继续上述操作,直到遍历完某节点所有连通的节点,此时map中存储的节点个数减去pre(初始为0),即可得到一组不为0数,用一个数组arr存储,直到所有节点全部遍历完,然后计算arr中的数即可得到最终结果。但是有问题遍历arr需要两层,应该提交不了,为此直接在遍历节点的同时计算最终结果(但是最终还是差几个用例没有通过,最后参考官方代码改进才通过)。
参考代码为:
class Solution(object):def countPairs(self, n, edges):""":type n: int:type edges: List[List[int]]:rtype: int"""map = {}for e in range(n):map[e] = []for key,value in edges:map[key].append(value)map[value].append(key)map2 = {}def dfs(cur_node):map2[cur_node] = 1arr = map[cur_node]count = 1for e in arr:if not map2.get(e,None):count += dfs(e)return countans = 0pre = 0for i in range(n):if not map2.get(i,None):count = dfs(i)ans += pre * countpre += countreturn ans
运行结果:

相关文章:

LeetCode:1402. 做菜顺序、2316. 统计无向图中无法互相到达点对数
1. 1402 做菜顺序 题目详细为: 一个厨师收集了他 n 道菜的满意程度 satisfaction ,这个厨师做出每道菜的时间都是 1 单位时间。 一道菜的 「 like-time 系数 」定义为烹饪这道菜结束的时间(包含之前每道菜所花费的时间)乘以这道菜…...

【消费战略】解读100个食品品牌|意面突起,“空刻”的品类心智占位!
空刻意面,一个开创意大利面速食化的新消费品牌,凭借着核心大单品意大利面,在过去短短的几年中,获得不俗的市场成绩和品牌影响力,占领了空刻意面的消费心智: 2019年,AIRMETER氢刻意面上线天猫旗舰…...

地图金字塔所在块的经纬度方位
地图金字塔所在块的经纬度方位 算法 #define LON_SPAN 360.0 // 开始经度(最左端) #define LAT_SPAN 180.0 #define GLOBAL_LEFT -180.0 // 开始纬度(最上端) #define GLOBAL_TOP 90.0 #define GLOBAL_RIGHT 180.0 #define GLOBAL_BOTTOM -90.0 // 地球的纬度跨度(180-(-180))…...
【干货】Java函数式编程公式大全,收藏学习!
函数操作是现代编程领域中的核心概念之一,它以类似 Excel 表格的方式进行数据处理和计算。它的特点是使用公式和函数来描述数据之间的关系和计算逻辑;它允许我们以更高效、更有组织的方式管理和处理数据。 在函数式编程中,数据被组织成表格的…...
django基于Python的房价预测系统+爬虫+大屏可视化分析
欢迎大家点赞、收藏、关注、评论 文章目录 前言一、项目介绍二、开发环境三、功能需求分析1 数据采集功能设计2数据管理功能设计3爬虫功能需求分析4 数据可视化功能需求分析数据库表的设计 四、核心代码五、效果图六、文章目录 前言 房价是一个国家经济水平的重要体现ÿ…...

异地组网企业怎么办理手续?
对于那些具有异地分支机构的企业来说,SDWAN(Software Defined Wide Area Network)可以是 提供高性能通信和数据传输的理想解决方案。那么,对于企业来说,SDWAN异地组网需要办理哪 些手续呢?下面将介绍一些关键的办理步骤。 1. 资质准备&…...

Android 13.0 根据包名授予OP_REQUEST_INSTALL_PACKAGES权限
1.概述 在系统13.0的定制化开发中,对于在app中调用安装第三方app的时候,会在这时弹出安装未知来源弹窗,需要默认授予REQUEST_INSTALL_PACKAGES 权限,来安装第三方app的安装未知来源权限,所以就是今天需要解决的这个问题 2.根据包名授予OP_REQUEST_INSTALL_PACKAGES的核心…...
乘客高铁出行调查:从需求到满意)
民安智库(湖北知名满意度测评公司)乘客高铁出行调查:从需求到满意
随着科技的飞速发展,高铁已成为我们日常出行的重要选择。然而,什么样的服务才是乘客真正需要的?什么样的调查才能真实反映乘客的感受?民安智库(政务服务第三方评估公司)作为一家中国独立第三方调研咨询的公…...

Oracle的dbms.rls实现数据访问控制
在大部份系统中,权限控制主要定义为模块进入权限的控制和数据列访问权限的控制(如:某某人可以进入某个控制,仓库不充许查看有关部门的字段等等)。 但在某些系统中,权限控制又必须定义到数据行访问权限的控制,此需求一般…...

Python 自定义函数的基本步骤
一、Python 自定义函数的基本步骤 1、什么是函数 函数,其实我们一开始学 Python 的时候就接触过。 不过我们使用的大多数都是 Python 的内置函数。 比如基本每个章节都会出现的 print() 函数。 而现在,我们主要学习的是自定义函数。 各位有没有想过…...

阿里云新品云服务器实例,经济型e实例,价格便宜,性价比高
前不久,阿里云推出了一款全新云服务器实例,他是阿里云面向个人开发者、学生、小微企业,在中小型网站建设、开发测试、轻量级应用等场景推出的全新入门级云服务器,基于“飞天CIPU”黄金技术架构设计,可轻松满足网站建设…...
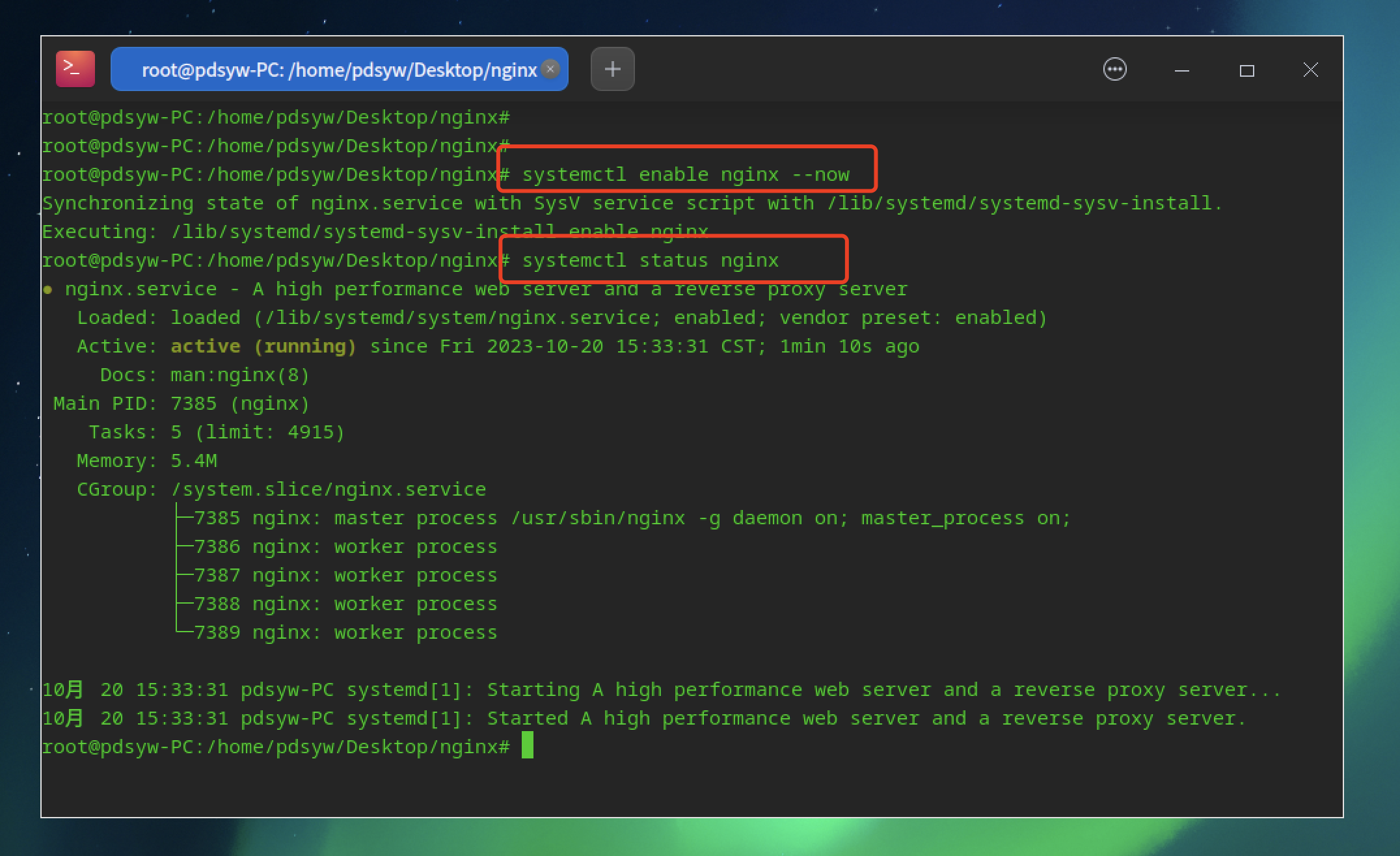
统信操作系统UOS上安装arm64版nginx
原文链接:统信操作系统UOS上安装arm64版nginx hello,大家好啊,今天给大家带来一篇在统信桌面操作系统UOS上安装arm64版nginx的文章,本篇文章主要是给大家提供一种下载离线nginx软件包的方法,拿到软件包可以去不能链接互…...
2017年高热度编程语言简介
世上语言千千万,我却独爱这一种!”这句话用来形容程序员和编程语言之间的爱恨情仇实在是再精准不过了。根据GitHub 2016年的开源报告,其上所有开源项目共包含了316种编程语言,这是一个什么概念呢?举个例子来说,世界上共有226个国…...
python爬虫入门(一)web基础
HTTP基本要点 HTTP请求,由客户端向服务端发出,可以分为 4 部分内容:请求方法(Request Method)、请求的网址(Request URL)、请求头(Request Headers)、请求体(…...

利用TreeMap来解决P3029 [USACO11NOV] Cow Lineup S
P3029 [USACO11NOV] Cow Lineup S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 好了,我们首先要统计奶牛的种类数量n,好与接下来我们记录一个范围内的奶牛的数量作比较,一旦我们统计范围内的奶牛的数量m达到我们刚开始记录的奶牛的数量n我…...
zzy-project-cli,提供多个框架的脚手架
npm地址 install npm install zzy-project-cli -g做什么? 将多个可选的框架提供给使用者选择,选中后自动下载对应模板,快捷使用。 使用 step1 zzy-cli create [项目名称]step2 获取模板之后选取任一进行下载 下载完成之后即可使用 模…...

C++类和对象中(构造函数,析构函数,拷贝构造函数)详解
C类和对象中[构造函数,析构函数,拷贝构造函数]详解 一.前言1.类的6个默认成员函数 二.构造函数1.构造函数的引出2.无参构造函数3.缺省参数在构造函数中的应用4.编译器实现的默认构造函数5.广义的默认构造函数6.默认构造函数的形成规则 三.析构函数1.析构函数的语法2.编译器实现…...
智能矩阵系统解决的问题?
智能矩阵系统可以解决的问题多种多样,它主要通过人工智能技术应用于矩阵系统,解决一些传统方法难以处理的问题。 以下是一些常见的应用场景: 1. 数据管理:智能矩阵系统可以有效地管理大量的数据,包括数据的存储、检索…...
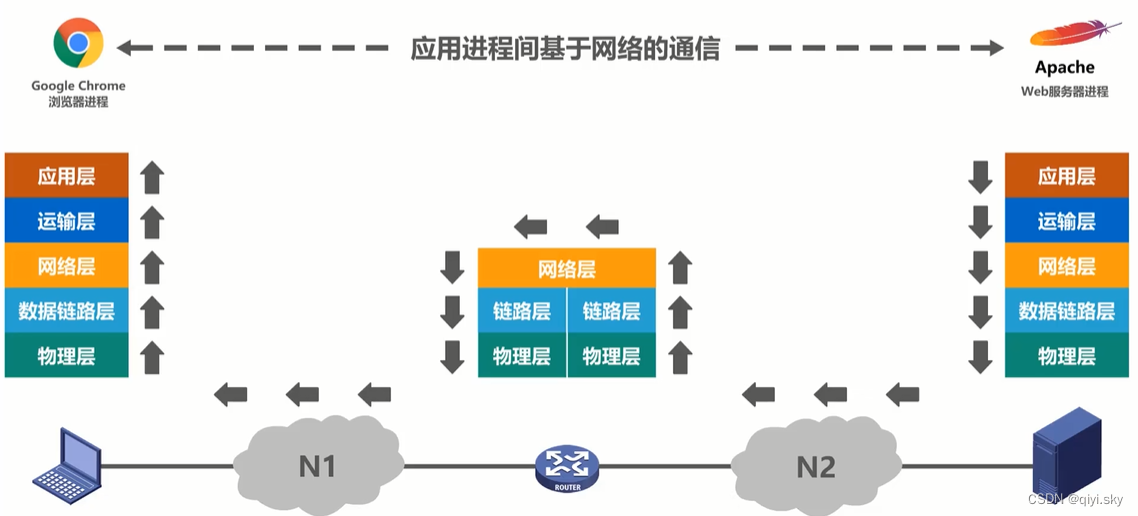
计算机网络——计算机网络体系结构(3/4)-计算机网络体系结构分层思想举例
目录 发送请求报文 应用层构建HTTP请求报文 运输层添加TCP首部 网络层添加IP首部 数据链路层形成帧 物理层转化为比特流 路由器处理 服务器处理 发回响应报文 计算机网络体系结构分层思想举例 假设网络拓扑如下所示,主机属于网络N1,Web服务器属…...
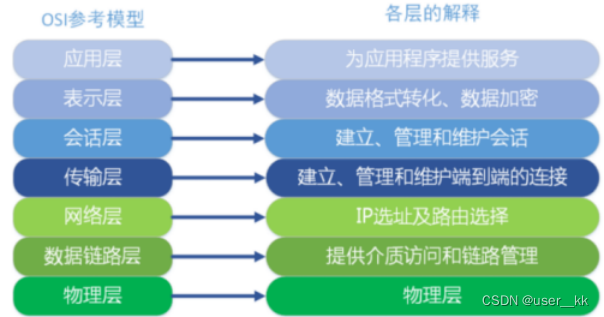
计算机网络,网络(OSI)七层模型,三次握手四次挥手,get与post请求区别,网络IO(BIO\NIO\AIO),TCP与UDP区别
1.OSI模型? 开放式系统互联通信参考模型(Open System Interconnection Reference Model) OSI网络七层模型:应用层、表示层、会话层、传输层、网络层、数据链路层、物理层 TCP/IP协议群简化了OSI七层模型:应用层、传输层、网络层、数据链路…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...