buu [NCTF2019]babyRSA 1
题目描述:
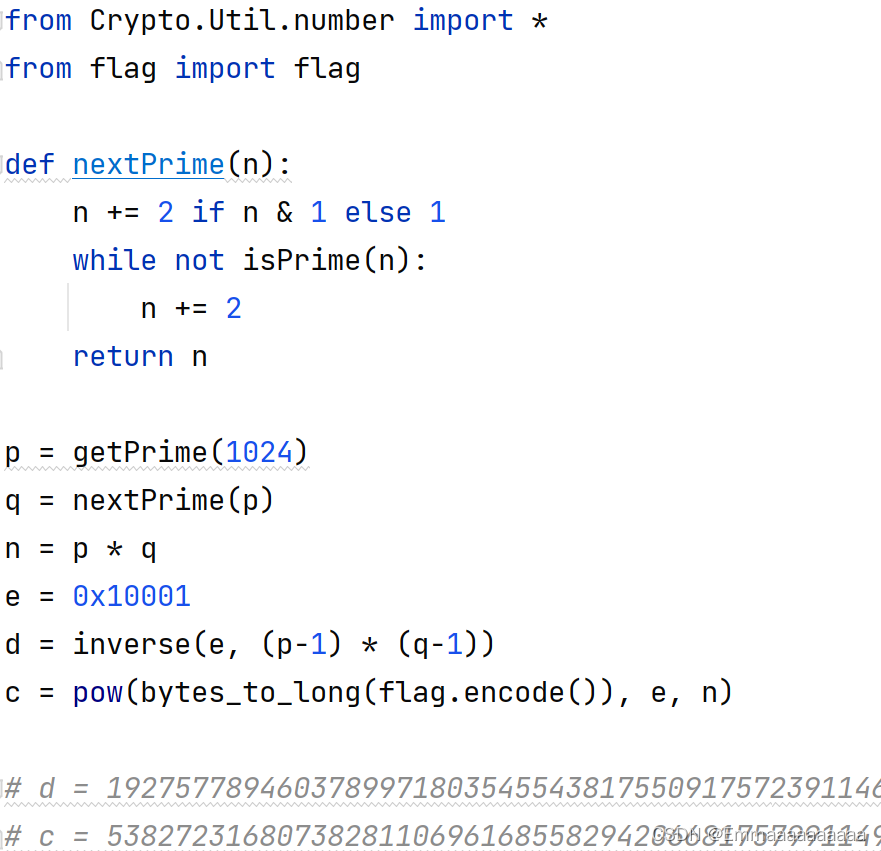
题目分析:
- 首先明确两个公式:
e*d = 1 mod (p-1)(q-1)
ed1 = e*d - 1 = k(p-1)(q-1)
- 想要解出此题,我们必须知道n,而要知道n,我们要知道p和q的值
- 通过 e*d 的计算,我们知道其长度为2066位,而生成p的条件为 getPrime(1024),所以(p-1)(q-1)应该为2048位
此处所说的位数长度是以Bit为单位,加一减一都不影响位数,相乘的话即为位数相加,这些性质记住就好,以下是计算代码:
from Crypto.Util.number import *
e = 65537
d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
print(gmpy2.bit_length(e*d))
# 2064
p = getPrime(1024)
print(gmpy2.bit_length(p))
# 1024
print(gmpy2.bit_length(p-1))
# 1024
- 又 ed1 = e*d - 1 = k(p-1)(q-1),2064-2048 = 16,所以k值必在 pow(2,15)至pow(2,16)之间
- 所以,我们可以利用此条件暴力求解k值,从而求出(p-1)*(q-1),间接求出 p 和 q 的值
- 那如何间接法呢?
- 首先我们求得了(p-1)(q-1),而p和q是两个相邻的质数,所以我们可以使用sympy库对p,q进行求解。思路为先对(p-1)(q-1)开方,再求得大于开方所得数和小于开方所得数的质数
p = sympy.prevprime(gmpy2.iroot((e*d-1)//i,2)[0])
q = sympy.nextprime(p)
- 其中 sympy.prevprime(x)是求大于x最近的质数,sympy.nextprime(x)是求小于x最近的质数。
- 解题代码如下:
import gmpy2
from Crypto.Util.number import long_to_bytes
import sympy
# e = 0x10001
e = 65537
d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804
p = 0
q = 0for k in range(pow(2,15),pow(2,16)):# pow(x,y) ---> x 的 y 次方# pow(x,y,z) ---> x 的 y 次方后,取余 zif (e*d-1)%k == 0:p = sympy.prevprime(gmpy2.iroot((e*d-1)//k,2)[0])# sympy.prevprime(x)是求大于x最近的质数# iroot(x,n) ---> x开n次根 ,返回值有两个,前一个是开方出来的整数部分,后一个是能否开出来,若能则为true,不能则为flaseq = sympy.nextprime(p)# sympy.nextprime(x)是求小于x最近的质数if (p-1)*(q-1) == (e*d-1)//k:breakn = p*q
m = pow(c,d,n)
m1 = long_to_bytes(m)
print(m1)
- 最终得出 flag{70u2_nn47h_14_v3ry_gOO0000000d}
收获与体会:
- 了解了一些字节的相关知识
- 知道了函数 sympy.prevprime(x)和sympy.nextprime(x)的相关知识
sympy.prevprime(x)是求大于x最近的质数
sympy.nextprime(x)是求小于x最近的质数 - 回顾了iroot(x,n) 和 pow(x,y) 的相关知识
iroot(x,n) —> x开n次根 ,返回值有两个,前一个是开方出来的整数部分,后一个是能否开出来,若能则为true,不能则为flase
pow(x,y) —> x 的 y 次方
pow(x,y,z) —> x 的 y 次方后,取余 z
相关文章:

buu [NCTF2019]babyRSA 1
题目描述: 题目分析: 首先明确两个公式: e*d 1 mod (p-1)(q-1) ed1 e*d - 1 k(p-1)(q-1)想要解出此题,我们必须知道n,而要知道n,我们要知道p和q的值通过 e*d 的计算,我们知道其长度为2066位,而生成p的…...

Java:如何选择一个Java API框架
Java编程语言是一种高级的、面向对象的语言,它使开发人员能够创建健壮的、可重用的代码。Java以其可移植性和平台独立性而闻名,这意味着Java代码可以在任何支持Java运行时环境(JRE)的系统上运行。Java和Node js一样,是一种功能强大的通用编程…...

mt6735 MIC 音量的调整及原理介绍
[DESCRIPTION] MIC 音量的调整及原理介绍[SOLUTION] audio_ver1_volume_custom_default.h#define VER1_AUD_VOLUME_MIC \ 64,112,192,144,192,192,184,184,184,184,184,0,0,0,0,\ 255,192,192,180,192,192,196,184,184,184,184,0,0,0,0,\ 255,208,208,180,255,208,196,0,0,0,0,…...
【深度学习】什么是线性回归逻辑回归单层神经元的缺陷
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录逻辑回归&线性回归单层神经元的缺陷单层神经元的缺陷逻辑回归&线性回归 线性回归预测的是一个连续值, 逻辑回归给出的”是”和“否”的回答. 等…...
Spring拦截器
SpringMVC提供了拦截器机制,允许运行目标方法之前进行一些拦截工作或者目标方法运行之后进行一下其他相关的处理。自定义的拦截器必须实现HandlerInterceptor接口。preHandle():这个方法在业务处理器处理请求之前被调用,在该方法中对用户请求…...

8个可能降低网站搜索引擎信任度的错误
如果觉得文章对你有用请点赞与关注,每一份支持都是我坚持更新更优质内容的动力!!!例如,发布一段质量差的网站内容不会完全破坏您的排名机会,只要您的内容策略的其余部分井井有条。但是本地SEO中存在一些错误…...

弱监督论文阅读:P2BNet算法笔记
标题:Point-to-Box Network for Accurate Object Detection via Single Point Supervision 会议:ECCV2022 论文地址:https://link.springer.com/10.1007/978-3-031-20077-9_4 官方代码:http://www.github.com/ucas-vg/P2BNet 作者…...

使用Java编写Hive的UDF实现身份证号码校验及15位升级18位
使用Java编写Hive的UDF实现身份证号码校验及15位升级18位 背景 在数仓项目中,有时候会根据身份证信息做一些取数filter或者条件判断的相关运算进而获取到所需的信息。古人是用Oracle做数仓,理所当然是用SQL写UDF【虽然SQL写UDF给SQL用就像用鸡肉饲养肉…...

前端:分享JS中7个高频的工具函数
目录 ◆1、将数字转换为货币 ◆2、将 HTML 字符串转换为 DOM 对象 ◆3、防抖 ◆4、日期验证 ◆5、将 FormData(表单数据)转换为 JSON ◆6、衡量一个函数的性能 ◆7、从数组中删除重复项 JavaScript 实用函数是有用的、可重复使用的片段࿰…...
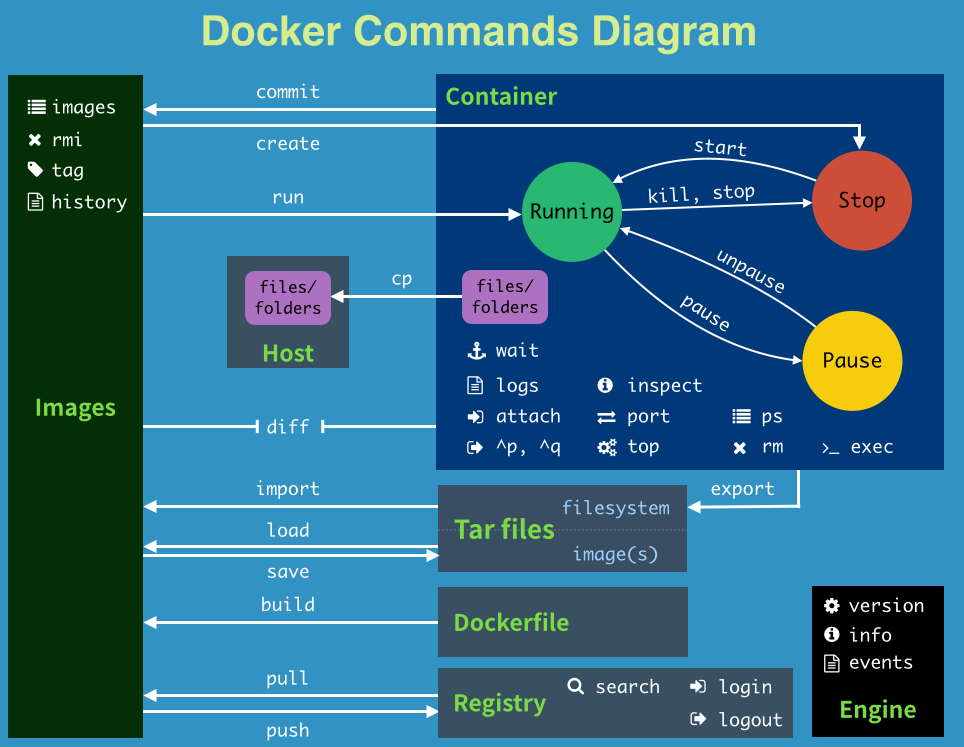
docker基础用法及镜像和容器的常用命令大全
1.docker 体系架构 Docker 采用了 C / S 架构,包括客户端和服务端。Docker 守护进程作为服务端接受来自客户端的请求,并处理这些请求(创建、运行、分发容器)。客户端和服务端既可以运行在一个机器上,也可通过 socket 或…...
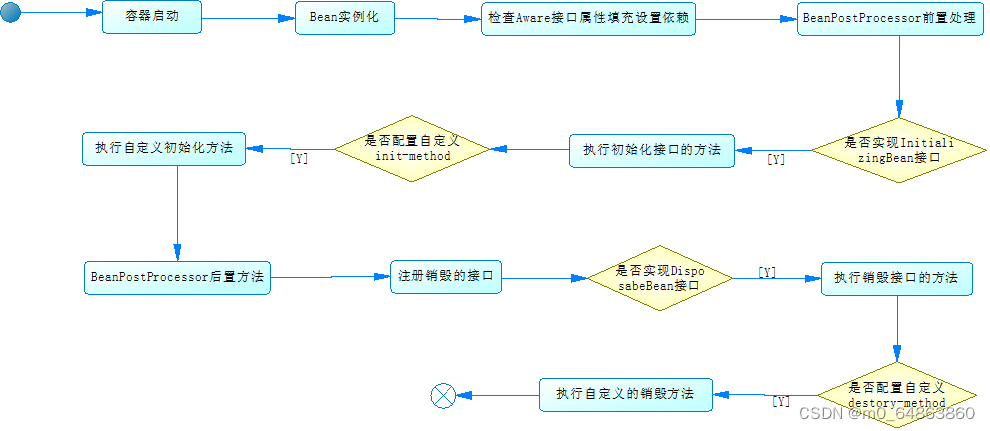
Spring(Bean生命周期)
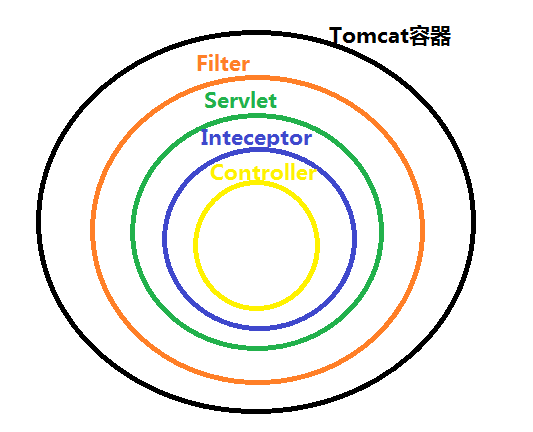
目录 1. 生命周期简图2. 扩展接口介绍 2.1 Aware接口2.2 BeanPostProcessor接口2.3 InitializingBean2.4 DisposableBean2.5 BeanFactoryPostProcessor接口3. spring的简化配置 3.1 项目搭建3.2 Bean的配置和值注入3.3 AOP的示例 1. 生命周期简图 2. 扩展接口介绍 2.1 Aware接…...

什么是分布式锁?几种分布式锁分别是怎么实现的?
一、什么是分布式锁: 1、什么是分布式锁: 分布式锁,即分布式系统中的锁。在单体应用中我们通过锁解决的是控制共享资源访问的问题,而分布式锁,就是解决了分布式系统中控制共享资源访问的问题。与单体应用不同的是&am…...

【一天一门编程语言】R 语言程序设计极简教程
R 语言程序设计极简教程 文章目录 R 语言程序设计极简教程R语言简介1.1 介绍1.2 R 语言的基础知识1.2.1 语法1.2.2 数据类型1.2.3 基本操作1.3 R 语言的高级知识1.3.1 函数1.3.2 包1.3.3 面向对象编程1.4 使用 R 语言的实践1.4.1 数据处理1.4.2 数据可视化1.4.3 数据建模1.4.3.…...

记一次顿悟的经历
2023.02.20 一次顿悟的经历 体验一次顿悟 需求: 为避免接收数据时一直阻塞,先调用 select 在一定时间内判断是否有数据可读 如果超时,就报错没读到数据,即使返回 如果仍然在 set 里,就调用 recv 函数接收数据 问…...
19_FreeRTOS软件定时器
目录 软件定时器介绍 FreeRTOS软件定时器特点 软件定时器的命令队列 软件定时器的相关配置 单次定时器和周期定时器 软件定时器结构体成员 FreeRTOS软件定时器相关API函数 实验源码 软件定时器介绍 定时器描述:从指定的时刻开始,经过一个指定时间,然后触发一个超时事件…...
值得推荐!安利5款良心又好用的小众软件
电脑上的各类软件有很多,除了那些常见的大众化软件,还有很多不为人知的小众软件,专注于实用功能,简洁干净、功能强悍。今天分享5个实用的软件,简单实用,效果拉满,堪称工作生活必备! …...
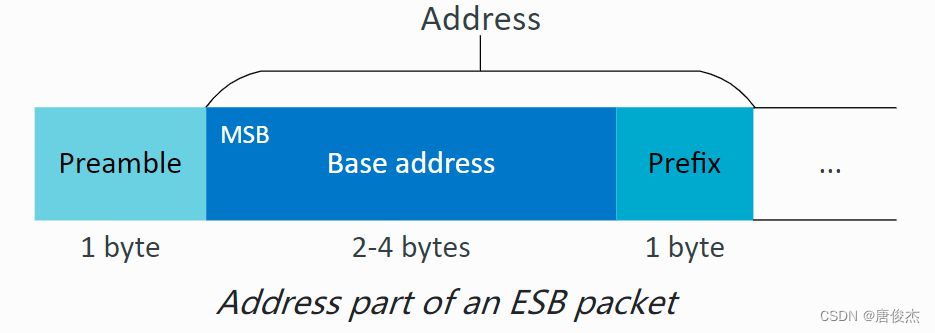
Enhanced ShockBurst (ESB)原文翻译
自我学习为主,同时也为所需要的提供一份资料 官方地址 增强型ShockBurst(ESB)是一种支持双向数据包通信的基本协议,包括数据包缓冲、数据包确认和丢失数据包的自动重传。ESB以低功耗提供无线通信,并且实现的代码量小且…...

软件测试之兼容性测试
对于基于计算机平台的软件,在测试过程中必须考虑软、硬件的兼容性,在设计测试用例的过程中必须考虑数据转换或转移的问题,应该尽力发现其可能带来的错误。不仅是基于计算机平台的软件,对于嵌入式软件也一样,在软件升级…...
——容器)
笔记(一)——容器
容器分类:序列式容器:每个元素都有固定位置,取决于插入的时机和地点,和元素无关,如vector、deque、list、stack、queue。关联式容器:元素位置取决于特定的排序准则,和插入顺序无关,如…...

C++入门:命名空间
假设这样一种情况,当一个班上有两个名叫 Zara 的学生时,为了明确区分它们,我们在使用名字之外,不得不使用一些额外的信息,比如他们的家庭住址,或者他们父母的名字等等。同样的情况也出现在 C 应用程序中。例…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...

统计按位或能得到最大值的子集数目
我们先来看题目描述: 给你一个整数数组 nums ,请你找出 nums 子集 按位或 可能得到的 最大值 ,并返回按位或能得到最大值的 不同非空子集的数目 。 如果数组 a 可以由数组 b 删除一些元素(或不删除)得到,…...
