详细介绍如何使用Ipopt非线性求解器求解带约束的最优化问题
本文中将详细介绍如何使用Ipopt非线性求解器求解带约束的最优化问题,结合给出的带约束的最优化问题示例,给出相应的完整的C++程序,并给出详细的解释和注释,以及编译规则等
一、Ipopt库的安装和测试
本部分内容在之前的文章《Ubuntu20.04安装Ipopt的流程介绍及报错解决方法(亲测简单有效)》中已经详细介绍过了,链接如下:
https://blog.csdn.net/qq_44339029/article/details/133679131
二、使用Ipopt非线性求解器求解带约束的最优化问题的程序示例
0、明确要求解的带约束的最优化问题
首先,我们来看一个简单的带约束的最优化问题,其包含两个不等式约束和1个等式约束,详情如下:
f = ( x 1 − 10.24 ) 2 + 5.21 x 2 + 9.9 ( x 3 − x 4 ) 2 f=(x_1-10.24)^2+5.21x_2+9.9(x_3-x_4)^2 f=(x1−10.24)2+5.21x2+9.9(x3−x4)2
g 1 : 2 ≤ x 3 − x 4 ≤ 10 g 2 : 2.99 ≤ x 2 ≤ 100 g 3 : x 2 = x 4 \begin{aligned}g_1 & : & 2\leq x_3-x_4\leq10\\ g_2 & : & 2.99\leq x_2\leq100\\ g_3 & : & x_2=x_4\end{aligned} g1g2g3:::2≤x3−x4≤102.99≤x2≤100x2=x4
其中 x 1 x_1 x1、 x 2 x_2 x2、 x 3 x_3 x3、 x 4 x_4 x4的取值范围均为0~100,易知使得上述目标函数 f f f取值最小的解为:10.24、2.99、4.99、2.99。
下面介绍,如何编程使用Ipopt非线性求解器求解该问题
1. 引入头文件和命名空间:
#include <iostream>
#include <cassert>
#include <cppad/ipopt/solve.hpp>
using CppAD::AD;
引入必要的C++头文件,包括iostream(用于输入输出),cassert(用于C风格的assert)以及cppad/ipopt/solve.hpp(用于Ipopt求解器和CppAD库的接口)。然后在一个匿名的命名空间中引入了AD类型,这是CppAD库中用于自动微分(Automatic Differentiation)的数据类型。
2. 定义FG_eval类:
namespace {class FG_eval {public:typedef CPPAD_TESTVECTOR(AD<double>) ADvector;void operator()(ADvector& fg, const ADvector& x) {// ...}};
}
在匿名命名空间中,定义一个FG_eval类,用于计算目标函数和约束条件的值。这个类也是调用使用CppAD和Ipopt库所需的最重要的接口,这个类中的operator()函数是用于计算问题的目标函数和约束条件的核心部分。它接受两个向量:fg用于存储目标函数值和约束条件值,x用于存储优化变量。
3. 定义operator()函数:
接下来,我们根据第0步中明确的目标函数及约束条件来编写核心的operator函数,示例如下:
void FG_eval::operator()(ADvector& fg, const ADvector& x) {assert(fg.size() == 4);assert(x.size() == 4);AD<double> x1 = x[0];AD<double> x2 = x[1];AD<double> x3 = x[2];AD<double> x4 = x[3];fg[0] = (x1 - 10.24) * (x1 - 10.24) + 5.21 * x2 + 9.9 * (x3 - x4) * (x3 - x4);fg[1] = x3 - x4;fg[2] = x2;fg[3] = x2 - x4;// 打印计算结果std::cout << "fg[0]:" << fg[0] << std::endl;std::cout << "fg[1]:" << fg[1] << std::endl;std::cout << "fg[2]:" << fg[2] << std::endl;std::cout << "fg[3]:" << fg[3] << std::endl;
}
operator()函数接受fg和x向量,然后根据问题的定义计算目标函数和约束条件的值,并将它们存储在fg向量中。同时,它也打印出这些值, 其中fg[0]即为目标函数表达式、fg[1]、fg[2]、fg[3]中依次对应了第0步中设定的三个约束,不等式约束直接写即可,等式约束的等式左右两边同时减去右边的项,使等式右边变为0。
4. 定义主函数get_started(该函数名字可任取):
定义一个主函数,设定自变量的初始值,以及自变量和约束的上下限,设定和提供调用Ipopt非线性求解器求解所需要的变量,然后调用求解器进行求解,并进行验证等操作,程序示例如下:
bool get_started(void)
{ bool ok = true;size_t i;typedef CPPAD_TESTVECTOR( double ) Dvector;size_t nx = 4;size_t ng = 3;Dvector xi(nx);xi[0] = 10.0;xi[1] = 5.0;xi[2] = 5.0;xi[3] = 100.0;Dvector xl(nx), xu(nx);for(i = 0; i < nx; i++){ xl[i] = 0;xu[i] = 100;}Dvector gl(ng), gu(ng);gl[0] = 2; gu[0] = 10;gl[1] = 2.99; gu[1] = 100;gl[2] = 0; gu[2] = 0;FG_eval fg_eval;std::string options;options += "Integer print_level 0\n";options += "String sb yes\n";options += "Integer max_iter 10\n";options += "Numeric tol 1e-6\n";options += "String derivative_test second-order\n";options += "Numeric point_perturbation_radius 0.\n";CppAD::ipopt::solve_result<Dvector> solution;CppAD::ipopt::solve<Dvector, FG_eval>(options, xi, xl, xu, gl, gu, fg_eval, solution);ok &= solution.status == CppAD::ipopt::solve_result<Dvector>::success;double check_x[] = { 10.24, 2.99, 4.99, 2.99 }; double rel_tol = 1e-6; // relative tolerancedouble abs_tol = 1e-6; // absolute tolerancefor(i = 0; i < nx; i++){ ok &= CppAD::NearEqual(check_x[i], solution.x[i], rel_tol, abs_tol ); std::cout << "x[" << i << "] = " << solution.x[i] << std::endl;}return ok;
}
以下是程序的详细解释:
(1). bool get_started(void):程序逻辑流程的主要函数,get_started函数定义了问题的基本参数,如变量数量、约束数量、变量的初始值,以及变量和约束的上下界。然后,它创建了一个FG_eval对象来计算目标函数和约束条件,设置了Ipopt求解器的选项,并最终调用求解器来解决问题。
(2). bool ok = true;:定义一个布尔变量 ok,用于表示问题是否成功求解。一开始将其初始化为 true。
(3). 类型别名 Dvector:通过 typedef CPPAD_TESTVECTOR(double) Dvector; 定义了一个 Dvector 类型,它是CppAD库中的向量类型,用于存储双精度(double)数值。
(4). size_t nx = 4;:定义一个 size_t 类型的变量 nx,表示问题中独立变量(自变量)的数量,即问题的变量维度。在这个示例中,有4个独立的自变量。
(5). size_t ng = 3;:定义一个 size_t 类型的变量 ng,表示问题中的约束数量,即约束的维度。在这个示例中,有3个约束条件。
(6). 创建 Dvector 向量 xi:用于存储问题的独立变量(自变量)。这个向量有4个元素,对应于4个自变量。
(7). 设置初始猜测值 xi:为 xi 向量中的每个元素分别赋初值,为检验算法性能,这里设定了一个较差的初始值。
- `xi[0] = 10.0;`- `xi[1] = 5.0;`- `xi[2] = 5.0;`- `xi[3] = 100.0;`
(8). 定义变量和约束条件的上下界:
- 创建 Dvector 向量 xl 和 xu,它们分别表示变量的下界和上界,并根据第0步中的设定的自变量的取值范围0~100进行设定
- 创建 Dvector 向量 gl 和 gu,它们分别表示约束条件的下界和上界,并根据第0步中,三个约束的进行设定,对于前两个不等式约束,直接设定即可,第三个等式约束,即 x 2 − x 4 = 0 x_2-x_4=0 x2−x4=0,因此,上下限均设为0即可。
(9). 创建 FG_eval 类的对象 fg_eval:FG_eval 即我们第二步中设定的类,用于计算目标函数和约束条件的值。这是问题的目标函数和约束条件的具体定义。
(10). 创建字符串 options:用于存储Ipopt求解器的选项,包括设置输出级别、最大迭代次数、收敛容差等,详情如下所示:
- `options += "Integer print_level 0\n";`:将输出级别设置为0,以关闭求解器的详细输出,只打印关键信息。- `options += "String sb yes\n";`:使用平衡约束优化方法。- `options += "Integer max_iter 10\n";`:设置最大迭代次数为10次。- `options += "Numeric tol 1e-6\n";`:设置迭代停止的收敛容差为1e-6。- `options += "String derivative_test second-order\n";`:启用二阶导数测试,用于检查目标函数和约束条件的导数是否正确。- `options += "Numeric point_perturbation_radius 0.\n";`:将随机扰动的半径设置为0,表示不使用扰动进行数值近似求导。
(11). 创建 CppAD::ipopt::solve_result<Dvector> solution;:用于存储求解结果的对象。
(12). 调用 CppAD::ipopt::solve 函数:使用Ipopt求解器解决非线性规划问题。传递了问题选项、独立变量的初始值、变量的上下界、约束条件的上下界、问题的定义(fg_eval 对象),以及存储结果的 solution 对象。
(13). 检查求解器的状态:如果状态为成功(success),则将 ok 变量保持为真,表示问题已成功求解。
注:下面的第(14)~(16)部分,是为了验证求解是否正确,为非必要步骤
(14) 创建 check_x 数组:包含问题的精确解。这些值是问题的已知精确解。
(15). 设置相对容差和绝对容差的阈值:这些值用于控制验证解的精度。
(16). 遍历问题中的每个变量,进行解的验证:使用 CppAD::NearEqual 函数来比较问题的解与精确解是否足够接近。如果它们的差距在相对容差和绝对容差的范围内,ok 变量将保持为真,并打印每个变量的解。
(17).返回 ok 变量:表示问题是否成功求解。
5. C++主函数main:
int main(void) {std::cout << "===== Ipopt with CppAD Testing =====" << std::endl;bool result = get_started();std::cout << "Final checking: " << result << std::endl;
}
main函数是程序的入口点,它简单地调用get_started函数来执行非线性规划问题的求解,并打印结果。
6. ☆☆☆带详细注释的完整程序`☆☆☆
# include <iostream>
// C style asserts
# include <cassert>
// 包含Ipopt求解器头文件
# include <cppad/ipopt/solve.hpp>// 在一个匿名的命名空间中,引入了一个AD类型,它是CppAD库中用于自动微分(Automatic Differentiation)的数据类型。AD类型可以用来表示变量和函数,使其具备微分能力。
namespace {using CppAD::AD;class FG_eval {public:typedef CPPAD_TESTVECTOR( AD<double> ) ADvector;// fg: function that evaluates the objective and constraints using the syntax// 定义一个函数运算符,用于计算目标函数和约束条件的值void operator()(ADvector& fg, const ADvector& x){ //使用assert来设定fg和x的大小,以确保它们与问题的维度匹配//fg 向量用于存储目标函数值和约束条件值,x向量用于存储优化变量assert( fg.size() == 4 );assert( x.size() == 4 );// 将 x 中的优化变量分配给 AD 类型的变量 x1 到 x4。这是在使用C++ Algorithmic Differentiation(CppAD)时定义问题中的独立变量的方式。AD<double> x1 = x[0];AD<double> x2 = x[1];AD<double> x3 = x[2];AD<double> x4 = x[3];// 计算目标函数的值,将其存储在 fg[0] 中。这里使用了 x1 到 x4 这些 AD 类型的变量,这意味着这个表达式将被自动微分,以便后续的梯度计算。fg[0] = (x1-10.24) * (x1-10.24) + 5.21*x2 + 9.9*(x3-x4)*(x3-x4);// 分别计算三个约束条件的值,并将它们存储在 fg[1] 和 fg[2]、 fg[3]中。fg[1] = x3-x4;fg[2] = x2;fg[3] = x2-x4;//std::cout << "fg[0]:" << fg[0]<< std::endl;std::cout << "fg[1]:" << fg[1]<< std::endl;std::cout << "fg[2]:" << fg[2]<< std::endl;std::cout << "fg[3]:" << fg[3]<< std::endl;return;}};
}// 该函数用于设置和解决非线性规划问题
// 它首先定义了问题的一些基本参数,如变量数量、约束数量、变量的初始值、变量和约束的上下界等
// 然后创建一个FG_eval对象用于计算目标函数和约束条件
// 最后,使用CppAD::ipopt::solve函数来解决问题,并将结果存储在solution中
bool get_started(void)
{ bool ok = true;size_t i;// 创建了一个类型别名 Dvector,它是CppAD库中的一个向量类型,用于存储双精度(double)数值。这个向量类型是CppAD库的一部分,通常用于存储问题的变量、约束和其他向量。typedef CPPAD_TESTVECTOR( double ) Dvector;// 声明了一个 size_t 类型的变量 nx,它表示问题中独立变量(自变量)的数量,也就是问题的变量维度。在这个示例中,有4个独立变量,因此 nx 的值为4。size_t nx = 4;// 声明了一个 size_t 类型的变量 ng,它表示问题中的约束数量,也就是约束的维度。在这个示例中,有3个约束条件,因此 ng 的值为3。size_t ng = 3;// 创建了一个名为 xi 的 Dvector 类型的向量,用于存储问题的独立变量(自变量)。这个向量有4个元素,对应于4个自变量。Dvector xi(nx);// 分别为这4个独立变量设置了初始值。这些值将用作问题的初始猜测,作为非线性规划求解器的起点。xi[0] = 10.0;xi[1] = 5.0;xi[2] = 5.0;xi[3] = 100.0;//设置问题的变量(自变量)和约束条件的上下界(限制条件)。Dvector xl(nx), xu(nx);for(i = 0; i < nx; i++){ xl[i] = 0;xu[i] = 100;}Dvector gl(ng), gu(ng);gl[0] = 2; gu[0] = 10;gl[1] = 2.99; gu[1] = 100;gl[2] = 0; gu[2] = 0;// 创建了 FG_eval 类的对象 fg_eval,用于计算目标函数和约束条件的值。这是问题的目标函数和约束条件的具体定义。FG_eval fg_eval;// 创建了一个字符串 options,用于存储Ipopt求解器的选项。std::string options;// 设置了求解器选项,将 print_level 参数设置为0,以关闭求解器的输出,即不会在控制台打印详细信息,只打印关键信息。options += "Integer print_level 0\n";// 将 sb 参数设置为 "yes",这表示使用平衡约束优化方法。options += "String sb yes\n";// 设置最大迭代次数为10次。options += "Integer max_iter 10\n";// approximate accuracy in first order necessary conditions;// see Mathematical Programming, Volume 106, Number 1,// Pages 25-57, Equation (6)// 设置迭代停止的收敛容差为1e-6。options += "Numeric tol 1e-6\n";// 启用了二阶导数测试,用于检查目标函数和约束条件的导数是否正确。options += "String derivative_test second-order\n";// maximum amount of random pertubation; e.g.,// when evaluation finite diff// 将随机扰动的半径设置为0,表示不使用扰动进行数值近似求导。options += "Numeric point_perturbation_radius 0.\n";// 创建了一个用于存储求解结果的对象 solution,CppAD::ipopt::solve_result<Dvector> solution;// 调用了 CppAD::ipopt::solve 函数,用于解决非线性规划问题。它传递了问题选项、独立变量的初始值、变量的上下界、约束条件的上下界、问题的定义(fg_eval 对象),以及存储结果的 solution 对象。CppAD::ipopt::solve<Dvector, FG_eval>(options, xi, xl, xu, gl, gu, fg_eval, solution);//检查求解器的状态,如果状态为成功(success),则 ok 变量将保持为真。这表示问题已成功求解。ok &= solution.status == CppAD::ipopt::solve_result<Dvector>::success;// 创建一个名为 check_x 的数组,其中包含了问题的精确解。这个数组中的值是问题的已知精确解。double check_x[] = { 10.24, 2.99, 4.99, 2.99 }; // 设置了相对容差和绝对容差的阈值。这些值用于控制验证解的精度。double rel_tol = 1e-6; // relative tolerancedouble abs_tol = 1e-6; // absolute tolerance// 遍历问题中的每个变量,进行解的验证。for(i = 0; i < nx; i++){ //使用 CppAD::NearEqual 函数来比较问题的解 solution.x[i] 与精确解 check_x[i] 是否足够接近。如果它们的差距在相对容差和绝对容差的范围内,ok 变量将保持为真。ok &= CppAD::NearEqual(check_x[i], solution.x[i], rel_tol, abs_tol ); // 使用 std::cout 打印每个变量的解,以便在控制台上查看结果。std::cout << "x[" << i << "] = " << solution.x[i] << std::endl;}return ok;
}// main program that runs all the tests
int main(void)
{ std::cout << "===== Ipopt with CppAD Testing =====" << std::endl;bool result = get_started();std::cout << "Final checking: " << result << std::endl;
}
// END C++
三、编译验证
将上面第二部分,第6步中给出的完整的程序,保存为CppAD_Ipopt.cpp,然后在同一目录下,创建一个名为CMakeLists.txt的文件,接下来,我们需要在CMakeLists.txt文件中,编写编译规则,如下所示:
# 设置CMake的最低版本要求
cmake_minimum_required(VERSION 3.5)
# 项目名称
project(CppadIpoptDemo)
# 寻找Ipopt包(确保你已经安装了Ipopt和CppAD)
# find_package(Ipopt REQUIRED)
# 设置可执行文件的名称和源文件
add_executable(cppad_ipopt_demo CppAD_Ipopt.cpp)
# 包含Ipopt的头文件
# target_include_directories(cppad_ipopt_demo PRIVATE ${IPOPT_INCLUDE_DIRS})
# 链接Ipopt库
# target_link_libraries(cppad_ipopt_demo ${IPOPT_LIBRARIES})
TARGET_LINK_LIBRARIES(cppad_ipopt_demo ipopt)
保存,并关掉CMakeLists.txt文件,接下来就利用该文件对CppAD_Ipopt.cpp进行编译,在该目录下空白处,右键打开终端,依次输入以下四条语句
mkdir build
cd build
cmake ..
make

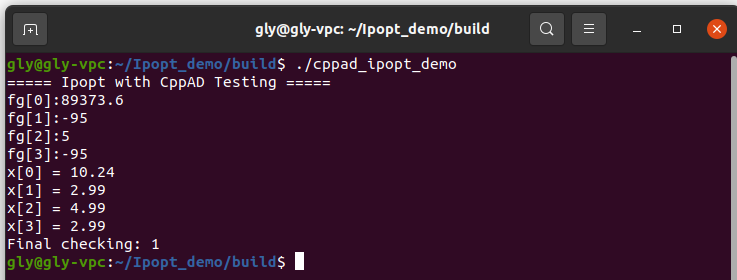
以上编译结束后,在build文件夹下,生成了可执行文件cppad_ipopt_demo,如下图所示

在当前目录下,右键打开终端,输入以下指令运行该文件
./cppad_ipopt_demo
运行结果如下,可以发现即使在给定的初始解很差的情况下,Ipopt非线性求解器依然能够求解出第二部分第0部步中设定的带约束优化问题的最优解。
相关文章:

详细介绍如何使用Ipopt非线性求解器求解带约束的最优化问题
本文中将详细介绍如何使用Ipopt非线性求解器求解带约束的最优化问题,结合给出的带约束的最优化问题示例,给出相应的完整的C程序,并给出详细的解释和注释,以及编译规则等 一、Ipopt库的安装和测试 本部分内容在之前的文章《Ubuntu2…...

跳跃游戏Ⅱ-----题解报告
题目:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 与Ⅰ不同的是,这次要求找出最小的跳跃次数。思路也很简单,在每一次跳跃之后都更新最远的跳跃距离。 举个列子: 输入:2,3,1,1,4 第一次…...
JVM 基础篇:类加载器
一.了解JVM 1.1什么是JVM JVM是Java Virtual Machine(Java虚拟机)的缩写,是一个虚构出来的计算机,是通过在实际的计算机上仿真模拟计算机功能来实现的,JVM屏蔽了与具体操作系统平台相关的信息,Java程序只需…...
文本批量处理,高效便捷的管理利器!
您是否曾经为了批量处理文本数据而烦恼?冗长的文本文件,繁琐的处理步骤,让您的工作变得异常困难。现在,我们向您推荐一款文本批量处理工具,它能够快速、准确地处理大量文本数据,让您的管理工作更加高效便捷…...
百度松果20231022作业
越狱 盒子与球 斯特林第二类数(用dp求)*盒子的阶乘 int dp[11][11]; //n>k int A(int x){int res1;fer(i,2,x1)res*i;return res; } signed main(){IOS;dp[2][1]dp[2][2]dp[1][1]1;fer(i,3,11){dp[i][1]1;fer(j,2,i){dp[i][j]j*dp[i-1][j]dp[i-1][j-…...
cropper+jq(图片裁剪上传)
<link rel"stylesheet" href"../../cropper/cropper.css"> <script type"text/javascript" src"../../cropper/cropper.js"></script> 没有引入jquery的原因 引入jquery <script src"../jquery-1.10.2.js…...

运行 `npm install` 时的常见问题与解决方案
运行 npm install 时的常见问题与解决方案 问题一:网络连接问题 描述: 运行 npm install 时,可能会遇到网络连接问题,导致无法正常下载依赖包。 报错示例: npm ERR! network connection timed outnpm ERR! connect…...
【2023年11月第四版教材】软考高项极限冲刺篇笔记(1)
1 你要接受一些观点 1、不明白的不要去试图理解了,死记硬背 2、要快速过知识点,卡住是不行的,慢也是没有任何作用的。 3、将厚厚的知识,变为薄薄的重点。标红必背 4、成熟度等级,很多知识领域都有,就是评价在一个领域达到的级别。 5、记得搜一下当年的高频科技词汇 6、选…...
http post协议发送本地压缩数据到服务器
1.客户端程序 import requests import os # 指定服务器的URL url "http://192.168.1.9:8000/upload"# 压缩包文件路径 folder_name "upload" file_name "test.7z" headers {Folder-Name: folder_name,File-Name: file_name } # 发送POST请求…...
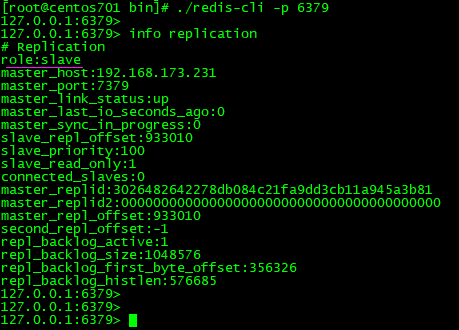
系列十三、Redis的哨兵机制
一、概述 Sentinel(哨兵)是Redis的高可用解决方案,由一个或者多个Sentinel实例组成集群,可以监视任意多个主服务器,以及这些服务器下属的所有从服务器,并在被监视的主服务器下线或者宕机时,自动…...

设置Unity URP管线中的渲染开关
在上一节中,我们添加了外轮廓线,但这个外轮廓线在所有使用该Shader的网格上是始终存在的。 如果我们想做一个开关,决定是否打开外轮廓线时,我们可以使用一个新的Uniform bool值,然后判断bool是否为true来开启外轮廓线…...
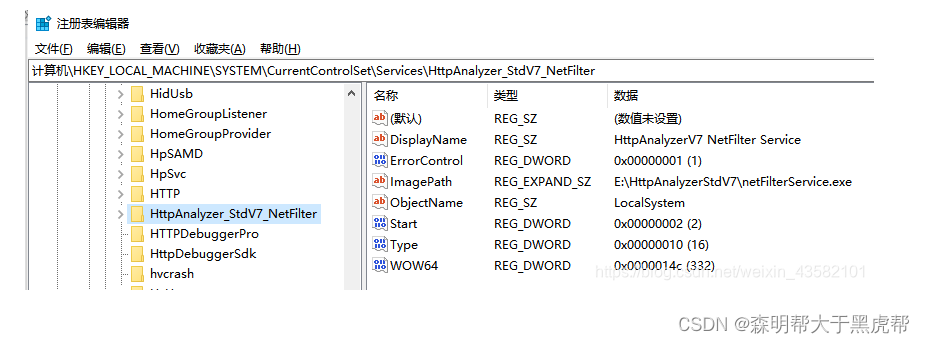
神器抓包工具 HTTP Analyzer v7.5 的下载,安装,使用,破解说明以及可能遇到的问题
文章目录 1、HTTP Analyzer 工具能干什么?2、HTTP Analyzer 如何下载?3、如何安装?4、如何使用?5、如何破解?6、Http AnalyzerStd V7可能遇到的问题 1、HTTP Analyzer 工具能干什么? A1:HTTP A…...

虚幻引擎:代理
一、代理类型 1.单薄代理 特点:允许有返回值,允许有参数,只可以一对一的传递消息就算绑定多个,但是总会被最后一个覆盖 2.多播代理 特点:不允许有返回值,允许有参数允许一对多传递消息 3.动态代理 …...

Openssl数据安全传输平台004:Socket C-API封装为C++类 / 服务端及客户端代码框架和实现
文章目录 0. 代码仓库1. 客户端C API2. 客户端C API的封装分析2.1 sckClient_init()和sckClient_destroy()2.2 sckClient_connect2.3 sckClient_closeconn()2.4 sckClient_send()2.5 sckClient_rev()2.6 sck_FreeMem 3. 客户端C API4. 服务端C API5. 服务端C6. 客户端和服务端代…...

网络协议--Traceroute程序
8.1 引言 由Van Jacobson编写的Traceroute程序是一个能更深入探索TCP/IP协议的方便可用的工具。尽管不能保证从源端发往目的端的两份连续的IP数据报具有相同的路由,但是大多数情况下是这样的。Traceroute程序可以让我们看到IP数据报从一台主机传到另一台主机所经过…...
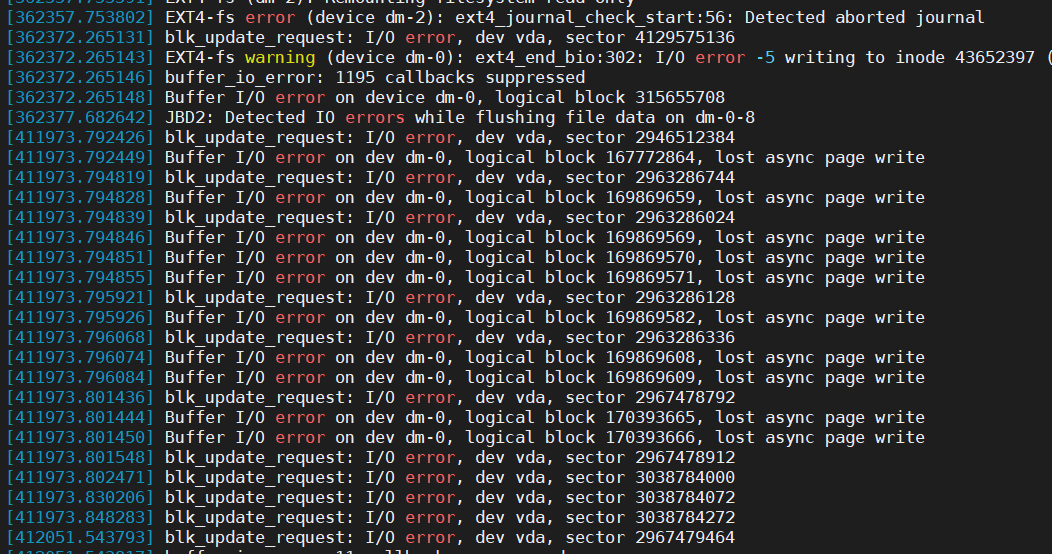
Centos磁盘问题小纪
场景说明 放个windows的图片镇楼,在给一个centos的来说明问题,咋了,好好的系统,啥也不能干了 来先上一波命令分析下问题 查看挂载 mount 重新挂载数据 mount -o remount, rw / 查看磁盘 df -h 查看分区挂载详情 rw读写权限 mount …...

计算机网络第三章习题
1.假定1km长的CSMA/CD网络的数据率为1Gb/s。设信号在网络上的传播 速率为200000km/s。求能够使用此协议的最短帧长. 问题刨析: 逻辑链: 最短帧长数据传输率x争用期2τ(2倍端到端所需要的时间) 题目已经给出数据率为1Gb/s,所以我们要知道争用期2τ是多少. 端到端所需要的时间信…...

Layui弹出层关闭后页面自动刷新的用法以及建议
首先在HTML中定义一个查询按钮 <div class"layui-inline"><button class"layui-btn" id"searchBtn" lay-submit lay-filter"data-search-btn" > <i class"layui-icon layui-icon-search">查询</i&…...
PHP 在线考试管理系统mysql数据库web结构layUI布局apache计算机软件工程网页wamp
一、源码特点 PHP 在线考试管理系统是一套完善的web设计系统 layUI技术布局 ,对理解php编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 PHP 在线考试系统1 代码 https://download.csdn.net/download/qq_41…...

【茫茫架构路】1. Class File字节码文件解析
本文所有内容的JDK版本为 OpenJDK 11 JDK11 Class File官方说明。 Java解析字节码文件源码参考,以下为部分字节码解析源码展示。 public ClassFile(DataInputStream in) {try {//magic: 0xCAFEBABEthis.magic ClassReader.readInt(in);System.out.println("m…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...

安全领域新突破:可视化让隐患无处遁形
在安全领域,隐患就像暗处的 “幽灵”,随时可能引发严重事故。传统安全排查手段,常常难以将它们一网打尽。你是否好奇,究竟是什么神奇力量,能让这些潜藏的隐患无所遁形?没错,就是可视化技术。它如…...
