当前位置： 首页 > news >正文

git将当前分支A强制推送远程分支pro上

news 2026/2/9 1:46:35

前言

开发中基于线上分支pro创建了A分支，开发完成之后。又基于线上分支pro创建了B分支，都以此合并到测试分支，两个分支更改中都动用部分共同的文件，这就导致后续开发合并代码越来越乱，这时你想把本地开发的分支强推到远程分支，覆盖远程仓库，同步代码。

1.查看当前分支
git branch
2.查看当前分支

origin 是远程自己仓库；upstream 是远程公司仓库

将本地分支A强制推送到名为"pro"的远程分支

git push -f origin A:pro

将分支pro强制推送到名为"dev"的远程分支，远程仓库pro的内容全部覆盖到dev分支

git push -f upstream pro:dev

注意此命令操作谨慎，做好代码备份

相关文章：

git将当前分支A强制推送远程分支pro上

前言 开发中基于线上分支pro创建了A分支，开发完成之后。又基于线上分支pro创建了B分支，都以此合并到测试分支，两个分支更改中都动用部分共同的文件，这就导致后续开发合并代码越来越乱，这时你想把本地开发的分支强推到…...

编程日记 2023/10/23 19:57:46

【计算机基础】存储器

目录 一.概念二.分类1．按存储介质分类2．按存储方式分类3．按存储器的读写功能分类4．按信息的可保存性分类5．按在计算机系统中的作用分类 三.主存区分SRAM、DRAM、Flash、DDR1.SRAM（静态随机存储器&#xff0…...

编程日记 2023/10/23 19:56:45

【LCR 159. 库存管理 III】

目录 一、题目描述二、算法原理三、代码实现 一、题目描述 二、算法原理 三、代码实现 class Solution { public:int getrandom(int left,int right,vector<int>& stock){return stock[rand()%(right-left1)left];}void qsort(int l,int r,vector<int>& s…...

编程日记 2023/10/23 19:55:43

Android ADB 常见问题和注意事项

Android ADB 常见问题和注意事项 在使用 ADB 过程中&#xff0c;可能会遇到一些常见问题和需要注意的事项&#xff1a; 1. USB 调试 要使用 ADB&#xff0c;你需要在设备上启用 USB 调试模式。这通常在设备的开发者选项中设置。如果你不能看到开发者选项&#xff0c;可以在设…...

编程日记 2023/10/23 19:53:42

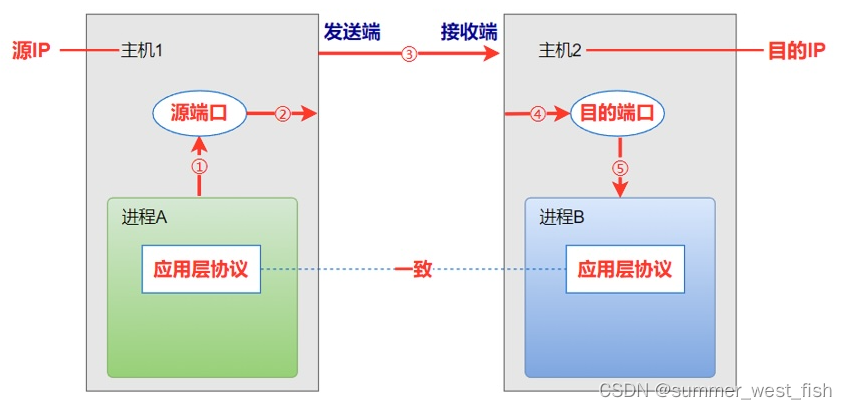
TCP/IP五元组

什么是五元组规则&#xff1f; 五元组是通信术语&#xff0c;英文名称为five-tuple,或5-tuple&#xff0c;五元组包括源IP地址(source IP)、源端口(source port)、目的IP地址(destination IP)、目的端口(destination port) 和 传输层协议(the layer 4 protocol)的五个量集合。…...

编程日记 2023/10/23 19:52:40

aiohttp ssl.SSLError: [SSL: SSLV3_ALERT_HANDSHAKE_FAILURE] 错误处理

这个问题原因吧其实就是3.10 开始官网更新了TLS 堆栈默认安全设置 感兴趣的可以看下链接 python官网叙述: Python 3.10 增加了 TLS 堆栈的默认安全设置 解决也很简单&#xff0c;将ssl安全等级降下来就行&#xff0c;例如&#xff1a; import ssl import aiohttp ctx ssl.cr…...

编程日记 2023/10/23 19:51:38

分析RPA流程自动化的挑战和解决方案

随着数字化工具和自动化解决方案的日益成熟&#xff0c;各行各业发掘到RPA机器人流程自动化技术的先进性&#xff0c;逐渐规模化部署RPA。 为了更好地推进RPA的实施&#xff0c;金智维在这里分享一些运用这项技术时面临的共同挑战&#xff0c;并给出针对性的解决方案。 组织架构…...

编程日记 2023/10/23 19:50:38

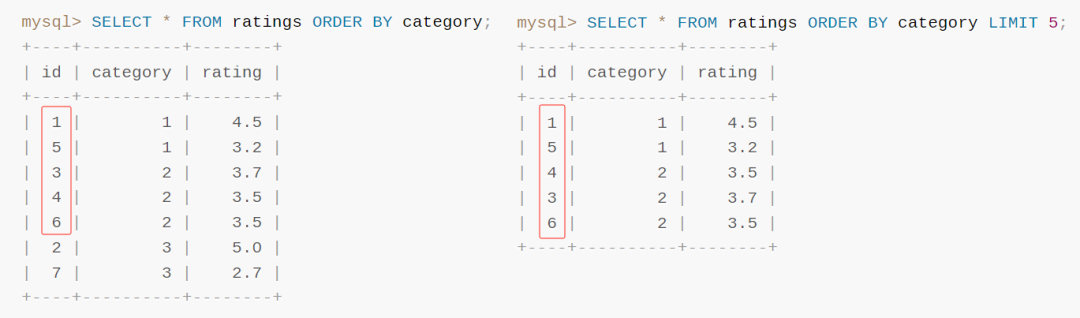
我试图扯掉这条 SQL 的底裤。只能扯一点点，不能扯多了

之前不是写分页嘛，分页肯定就要说到 limit 关键字嘛。 然后我啪的一下扔了一个链接出来： https://dev.mysql.com/doc/refman/8.0/en/limit-optimization.html 这个链接就是 MySQL 官方文档，这一章节叫做“对 Limit 查询的优化”，针对 limit 和 order by 组合的场景进行了较…...

编程日记 2023/10/23 19:49:37

LeNet（pytorch实现

LeNet 本文编写了一个简单易懂的LeNet网络&#xff0c;并在F-MNIST数据集上进行测试&#xff0c;允许使用GPU计算 在这里插入代码片 import torch from torch import nn, optim import d2lzh_pytorch as d2ldevice torch.device(cuda if torch.cuda.is_available() else cp…...

编程日记 2023/10/23 19:48:36

Selenium获取百度百科旅游景点的InfoBox消息盒

前面我讲述过如何通过BeautifulSoup获取维基百科的消息盒&#xff0c;同样可以通过Spider获取网站内容&#xff0c;最近学习了SeleniumPhantomjs后&#xff0c;准备利用它们获取百度百科的旅游景点消息盒&#xff08;InfoBox&#xff09;&#xff0c;这也是毕业设计实体对齐和属…...

编程日记 2023/10/23 19:47:35

springcloud笔记 (8) -网关 Gateway

网关 出国需要过海关 网关&#xff1a;网络的关卡 网关的作用 1&#xff1a;路由转发 2&#xff1a;安全控制 保护每个服务&#xff0c;不需要将每个暴露出去 3&#xff1a;负载均衡 1.没有网关&#xff1a;客户端直接访问我们的微服务&#xff0c;会需要在客户端配置很多…...

编程日记 2023/10/23 19:46:34

【C++编程语言】STL常用算法 算术生成和集合算法

1.算术生成算法概念 算法简介&#xff1a; accumlate 计算容器元素累计总和fill 向容器中添加元素 注意&#xff1a;算术生成算法属于小型算法 使用时包含头文件为#include<numeric> 2.accumulate /*函数原型&#xff1a;int accumulate(iterator beg ,iterator end…...

编程日记 2023/10/23 19:45:34

解放双手：VMLogin自动化工具的高效便捷

在现代工作环境中&#xff0c;时间和效率是我们追求的关键。幸运的是&#xff0c;随着技术的发展&#xff0c;自动化工具为我们提供了解放双手的机会。其中&#xff0c;防关联浏览器的自动化就是一种强大的工具&#xff0c;能够简化我们的工作流程并提升效率。本文将探讨浏览器…...

编程日记 2023/10/23 19:44:31

深度解析网络代理技术及其在网络安全和爬虫应用中的关键作用

在当今数字化时代&#xff0c;网络代理技术在维护网络安全、保护隐私以及实现高效数据获取方面发挥着不可或缺的作用。本文将全面解析Socks5代理、IP代理等关键技术&#xff0c;并探讨其在网络安全和爬虫开发中的重要作用。 1. Socks5代理与SK5代理&#xff1a;多功能代理协议…...

编程日记 2023/10/23 19:43:30

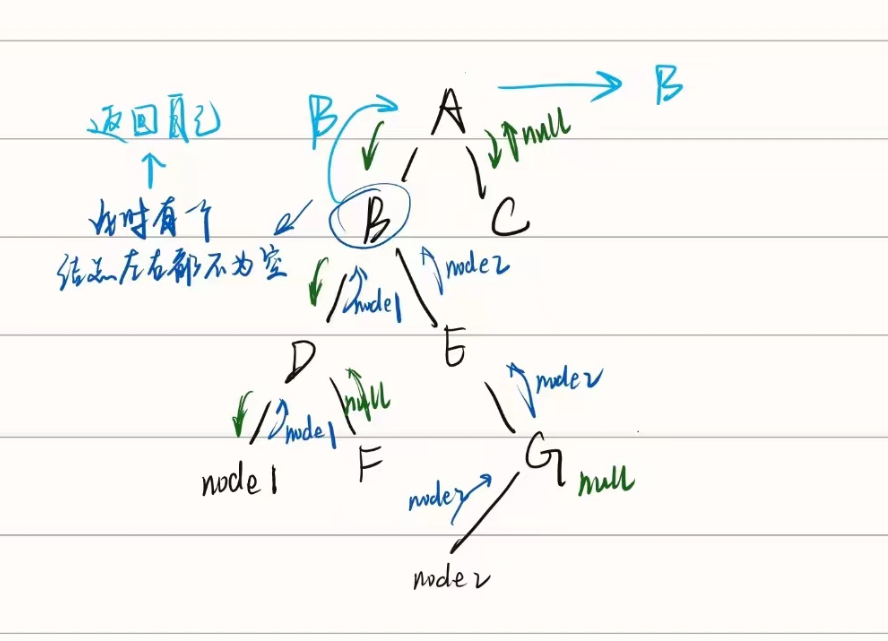
寻找二叉树的最低公共祖先节点

两个节点沿二叉树向上找&#xff0c;找到的第一个公共的节点 例&#xff1a;D和F之间的最低公共节点&#xff1a;B D → B&#xff1b; F → E → B&#xff1b; E和G最低公共节点&#xff1a;A E → B → A&#xff1b; G → C → A&#xff1b; B和F最低公共节点&#xff…...

编程日记 2023/10/23 19:42:29

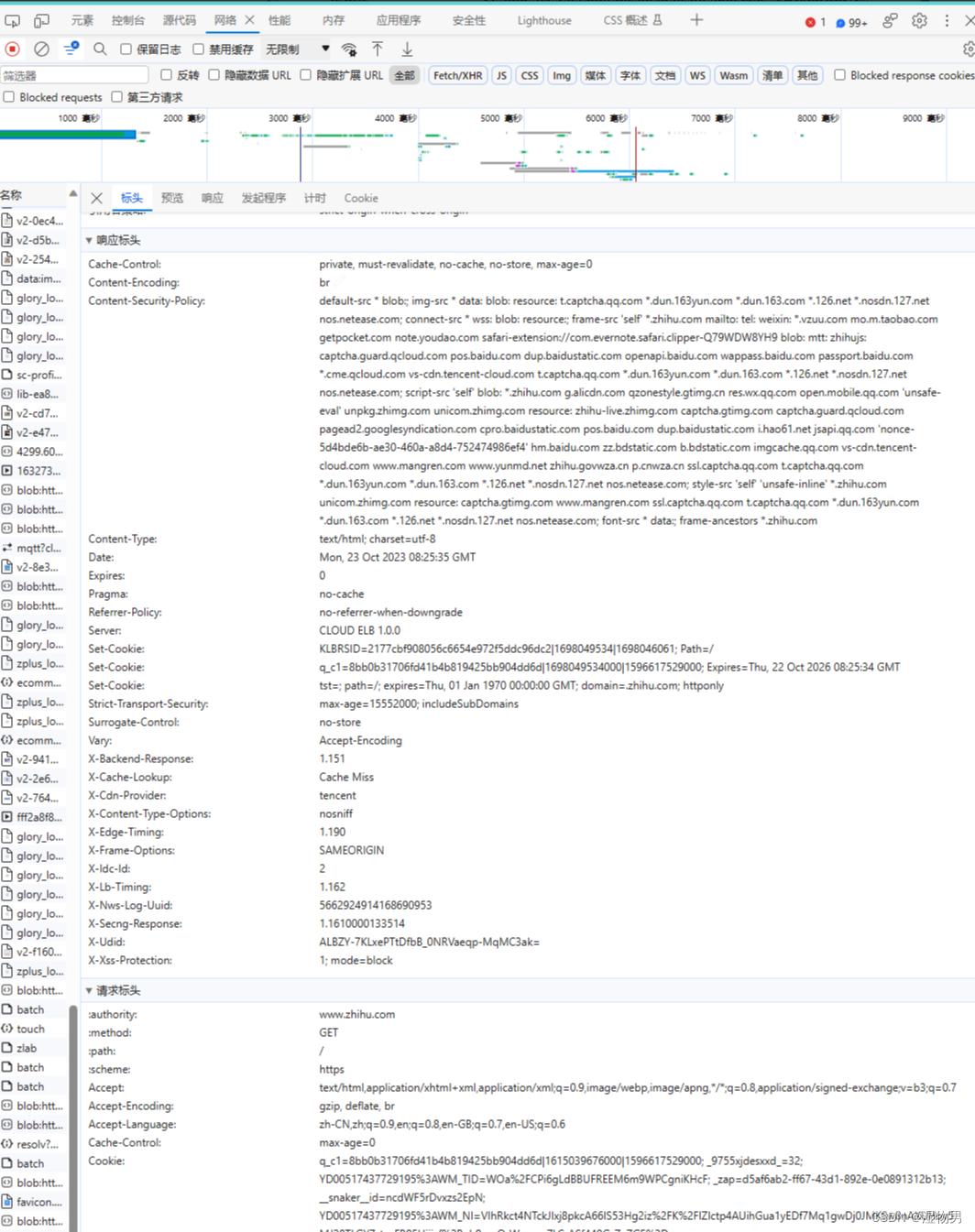
python网络爬虫（二）基本库的使用urllib/requests

使用urllib 了解一下 urllib 库&#xff0c;它是 Python 内置的 HTTP 请求库&#xff0c;也就是说不需要额外安装即可使用。它包含如下 4 个模块。 request&#xff1a;它是最基本的 HTTP 请求模块&#xff0c;可以用来模拟发送请求。就像在浏览器里输入网址然后回车一样&…...

编程日记 2023/10/23 19:40:28

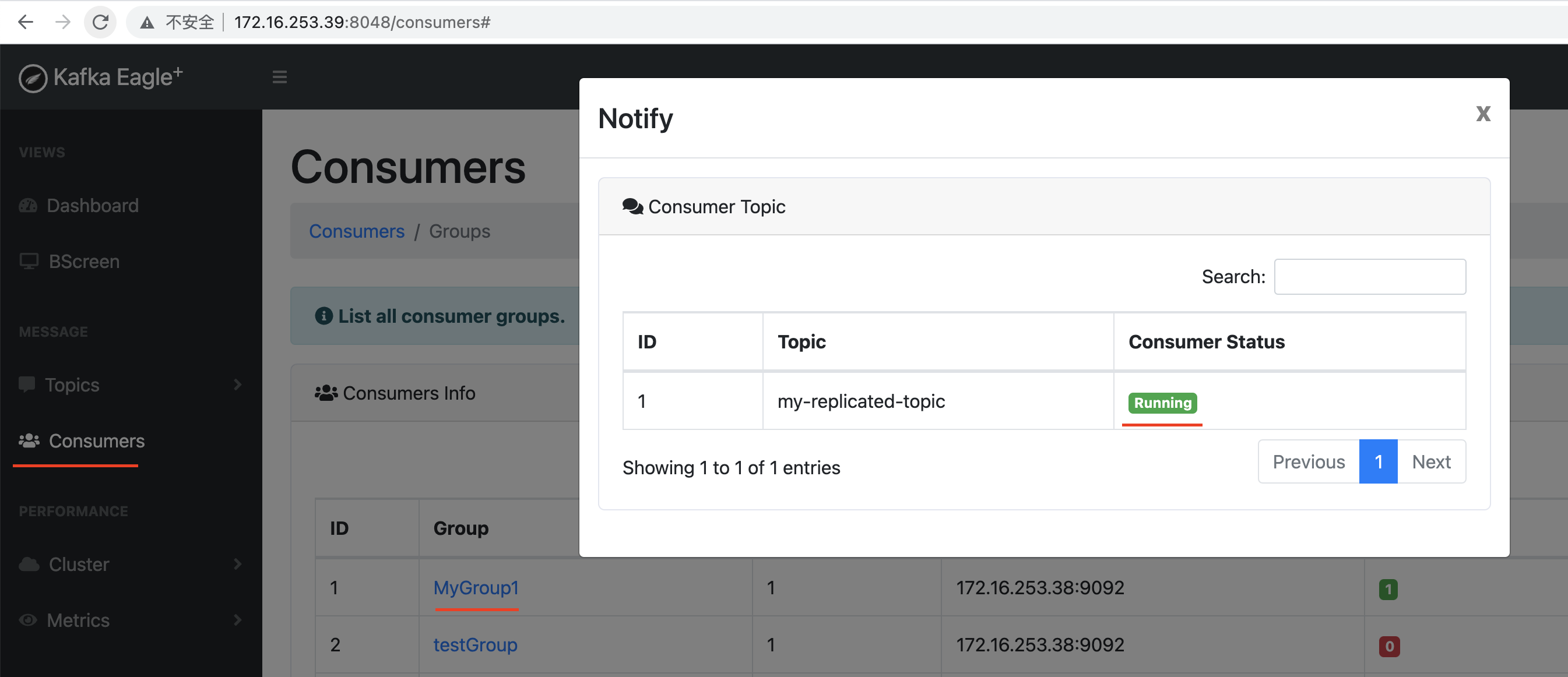
Kafka快速入门(最新版3.6.0)

文章目录 一、初识MQ1.1 什么是MQ1.2 同步和异步通讯1.1.1 同步通讯1.1.2 异步通讯 1.3 技术对比1.4 MQ的两种模式 二、初识Kafka2.1 Kafka的使用场景2.2 Kafka基本概念2.3 Topic与Partition 三、Kafka基本使用3.1 部署前的准备3.2 启动kafka服务器3.3 Kafka核心概念之Topic3.4…...

编程日记 2023/10/23 19:39:27

CTF/AWD竞赛标准参考书+实战指南：《AWD特训营》

作者简介&#xff1a; 懒大王敲代码&#xff0c;正在学习嵌入式方向有关课程stm32&#xff0c;网络编程&#xff0c;数据结构C/C等 欢迎大家点赞 &#x1f44d; 收藏 ⭐ 加关注哦&#xff01;&#x1f496;&#x1f496; 《AWD特训营》 前言 内容简介 读者对象 本书目录 前言…...

编程日记 2023/10/23 19:38:25

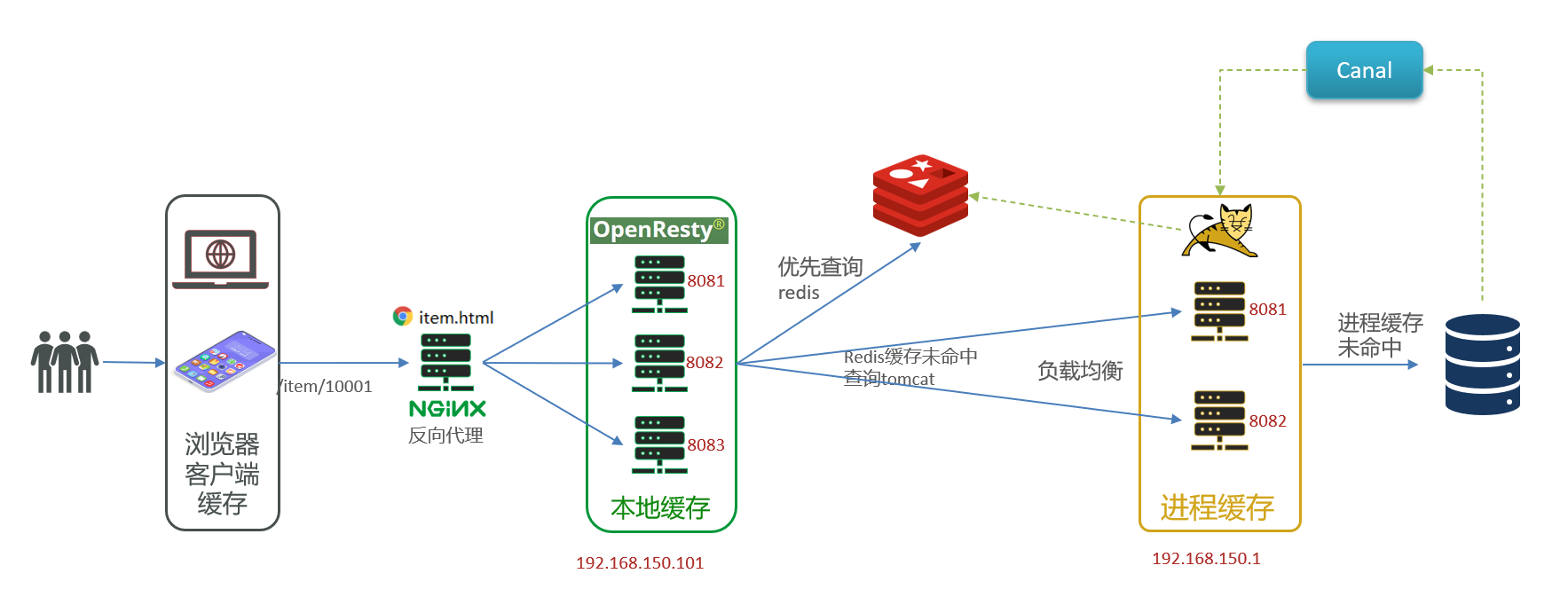
从零开始 Spring Cloud 15：多级缓存

从零开始 Spring Cloud 15&#xff1a;多级缓存 多级缓存架构 传统的缓存使用 Redis&#xff0c;大致架构如下&#xff1a; 这个架构存在一些问题&#xff1a; 请求要经过Tomcat处理&#xff0c;Tomcat的性能成为整个系统的瓶颈 Redis缓存失效时&#xff0c;会对数据库产生冲…...

编程日记 2023/10/23 19:37:24

Adobe产品2024

一、软件下载&#xff1a; 二、软件介绍&#xff1a; Adobe公司旗下的产品在影视后期、平面设计等领域有着无可取代的地位。在创意和设计领域中&#xff0c;产品有多达 21 个&#xff0c;包括 Photoshop、Illustrator、InDesign、Premiere Pro、After Effects 和 Acrobat Pro …...

编程日记 2023/10/23 19:36:23

未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？

编辑&#xff1a;陈萍萍的公主一点人工一点智能 未来机器人的大脑&#xff1a;如何用神经网络模拟器实现更智能的决策&#xff1f;RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战&#xff0c;在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

编程新知 2026/2/7 23:18:28

rknn优化教程（二）

文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK&#xff0c;开始写第二篇的内容了。这篇博客主要能写一下&#xff1a; 如何给一些三方库按照xmake方式进行封装&#xff0c;供调用如何按…...

编程新知 2025/6/11 15:25:30

【力扣数据库知识手册笔记】索引

索引 索引的优缺点 优点1. 通过创建唯一性索引&#xff0c;可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度&#xff08;创建索引的主要原因&#xff09;。3. 可以加速表和表之间的连接&#xff0c;实现数据的参考完整性。4. 可以在查询过程中&#xff0c;…...

编程新知 2026/1/25 4:36:37

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案

问题描述&#xff1a;iview使用table 中type: "index",分页之后 &#xff0c;索引还是从1开始&#xff0c;试过绑定后台返回数据的id, 这种方法可行&#xff0c;就是后台返回数据的每个页面id都不完全是按照从1开始的升序&#xff0c;因此百度了下&#xff0c;找到了…...

编程新知 2026/1/29 20:58:41

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现，论文初版实现

摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序&#xff0c;以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务&#xff0c;提供稳定高效的数据处理与业务逻辑支持&#xff1b;利用 uniapp 实现跨平台前…...

编程新知 2026/1/31 10:55:22

EtherNet/IP转DeviceNet协议网关详解

一&#xff0c;设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络&#xff0c;本网关连接到EtherNet/IP总线中做为从站使用&#xff0c;连接到DeviceNet总线中做为从站使用。 在自动…...

编程新知 2026/1/31 6:53:51

华为云Flexus+DeepSeek征文｜DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建

华为云FlexusDeepSeek征文&#xff5c;DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色&#xff0c;华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型&#xff0c;能助力我们轻松驾驭 DeepSeek-V3/R1&#xff0c;本文中将分享如何…...

编程新知 2026/2/2 2:30:58

LRU 缓存机制详解与实现（Java版） + 力扣解决

&#x1f4cc; LRU 缓存机制详解与实现&#xff08;Java版&#xff09; 一、&#x1f4d6; 问题背景 在日常开发中&#xff0c;我们经常会使用 缓存&#xff08;Cache&#xff09; 来提升性能。但由于内存有限&#xff0c;缓存不可能无限增长&#xff0c;于是需要策略决定&am…...

编程新知 2025/11/28 20:47:33

day36-多路IO复用

一、基本概念 &#xff08;服务器多客户端模型&#xff09; 定义&#xff1a;单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用&#xff1a;应用程序通常需要处理来自多条事件流中的事件&#xff0c;比如我现在用的电脑&#xff0c;需要同时处理键盘鼠标…...

编程新知 2026/1/31 7:42:50

从面试角度回答Android中ContentProvider启动原理

Android中ContentProvider原理的面试角度解析&#xff0c;分为​​已启动​​和​​未启动​​两种场景&#xff1a; 一、ContentProvider已启动的情况 1. ​​核心流程​​ ​​触发条件​​&#xff1a;当其他组件&#xff08;如Activity、Service&#xff09;通过ContentR…...

编程新知 2025/10/2 19:46:59