【密码学】 一篇文章讲透数字签名
【密码学】 一篇文章讲透数字签名
数字签名介绍
数字签名(又称公钥数字签名)是只有信息的发送者才能产生的别人无法伪造的一段数字串,这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。它是一种类似写在纸上的普通的物理签名,但是在使用了公钥加密领域的技术来实现的,用于鉴别数字信息的方法。一套数字签名通常定义两种互补的运算,一个用于签名,另一个用于验证。数字签名是非对称密钥加密技术与数字摘要技术的应用。
数字签名可以识别消息是否被篡改, 并验证消息的可靠性, 也可以防止否认。 在之前的博客文章中,我们介绍过消息认证码,它也可以防止消息被篡改,验证消息可靠性。 而数字签名与消息认证码的最大不同在于, 数字签名算法可以防止否认, 因为私钥只有签名者持有, 而消息认证码中的密钥由双方共享。常用的数字签名方法有三种,分别是RSA、 DSA和ECDSA。
数字签名原理
数字签名类似于现实世界中的盖章和签字, 它具有以下四大特征:
- 可验证性——接收者可以验证发送者签名的真实性和有效性;
- 不可伪造性——除签名者之外, 任何人不可伪造签名;
- 不可否认性——发送方不能否认自己所发送的签名;
- 数据完整性——能够提供对所签消息的完整性检验。
下面通过一个示例来说明数字签名是如何防止否认的:

Alice通过密钥生成算法生成密钥对;
2) Alice将公钥发送给Bob, 私钥自己保留;
3) Alice使用单向数列函数计算出合同的摘要值;
4) Alice使用私钥对消息摘要值进行签名;
5) Alice将合同和签名值分别发送至Bob;
6) Bob使用单向散列函数计算出合同的消息摘要值;
7) Bob使用Alice的公钥对签名进行验证, 若验证通过则说明合同内容完整且来自于Alice。
从本应用场景中可以看出, 虽然数字签名的工作模式与消息认证码较为相似, 但不同的是数字签名可防止否认。 消息认证码使用的密钥为对称密钥, 如果基于消息认证码完成消息的认证过程, 一旦Alice否认曾经向Bob发送过预订合同, 那么Bob将无法对Alice进行指控。 而数字签名算法中私钥只有Alice持有, 其他人无法对签名进行伪造, 这一特点也使得Alice无法对这一过程进行否认。
RSA数字签名算法
RSA数字签名算法基于RSA密钥系统实现, 在第8章中已经详细介绍了RSA算法。 RSA数字签名过程与RSA加解密过程较为相似, 但公钥和私钥的使用方法却存在明显区别。为了方便描述RSA数字签名过程, 此处依然借助假想场景加以说明, 在假想场景中:
1) Alice通过RSA密钥生成算法生成密钥对;
2) Alice将公钥发送给Bob, 私钥自己保留;
3) Alice使用RSA私钥对消息进行加密操作, 并将消息和签名结果分别发送给Bob;
4) Bob使用RSA公钥对签名进行解密操作, 判断解密结果和消
息是否一致。
此处Alice使用私钥对消息执行加密操作, 该加密操作可理解为对消息进行数字签名, 该私钥可称为签名密钥; Bob收到消息之后使用Alice的公钥执行解密操作, 该解密操作可理解为对消息执行数字签名验证, 该公钥可称为验证密钥。 总之, 在RSA数字签名中, 私钥用于加密消息, 公钥用于解密消息; 而在RSA加密中, 公钥用于加密消息, 而私钥用于解密消息。 无论如何, 公钥总是可以公开的, 而私钥却不能泄露。
RSA数字签名详细说明
RSA签名
RSA数字签名和RSA加密过程恰好相反, 签名过程使用私钥对数据执行加密操作, RSA数字签名表达式如下, 其中s为签名结果, m为消息(消息可以是明文也可以是消息摘要) 。
s ≡ mdmod n
###RSA验证签名
同样, 验证签名过程使用公钥对签名数据进行解密, RSA验证签名表达式如下, 其中s为签名结果, m’为解密结果。 验证签名过程判断m’≡mmod n, 成立则为有效签名, 不成立则签名无效。
m' ≡ semod n
由于参数e的值远小于参数d, 所以RSA验证签名的计算量小于RSA签名, 也就说RSA验证签名速度快于签名速度。
ECDSA数字签名
ECDSA算法基于椭圆曲线离散对数问题, 使用较短的密钥长度便可提供与RSA签名算法或DSA算法等同的安全等级, 密钥长度为160256位的椭圆曲线算法与密钥长度为10243072位的非椭圆曲线算法安全性相同。 椭圆曲线的基础知识可以参考我之前的博客。
ECDSA数字签名算法和DSA算法在概念上有紧密联系, 但其计算过程是在椭圆曲线群上完成的, 所以计算过程相差较大。 ECDSA算法与DSA算法相似, 该算法只能提供数字签名功能, 而不能用于加密或密钥交换。
ECDSA生成签名
ECDSA的签名结果由两部分构成: r和s。 其中r和s的长度与n相同, 例如在secp256r1曲线中, n的长度为256比特, r和s也分别为256比特, 不使用任何编码方式的情况下签名总长度为512比特。 假设消息为M, 单向散列函数为HASH()。 使用ECDSA对消息进行签名的计
算过程如下:
1) 选择一个随机数k, 满足条件0<k<n;
2) 计算R=k·G;
3) 计算z=HASH(M);
4) 设置r=xR, xR为点R的横坐标;
5) 计算s≡(z+d·r)k-1mod n;
6) 得到签名(r,s)。
ECDSA验证签名
在验证签名之前需确保已经得到签名者的公钥、 消息以及签名信息(r,s)。 验证签名的过程如下:
1) 计算w≡s-1mod n;
2) 计算z=HASH(M);
3) 计算u1≡(wz)mod n;
4) 计算u2≡(wr)mod n;
5) 计算P=u1·g+u2·Q;
6) 如果xP≡r mod n, 则签名有效, 否则签名无效, 其中xP为点P的横坐标。
相关文章:

【密码学】 一篇文章讲透数字签名
【密码学】 一篇文章讲透数字签名 数字签名介绍 数字签名(又称公钥数字签名)是只有信息的发送者才能产生的别人无法伪造的一段数字串,这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。它是一种类似写在纸上的普通的物理签名…...

POI导入导出、EasyExcel批量导入和分页导出
文件导入导出POI、EasyExcel POI:消耗内存非常大,在线上发生过堆内存溢出OOM;在导出大数据量的记录的时候也会造成堆溢出甚至宕机,如果导入导出数据量小的话还是考虑的,下面简单介绍POI怎么使用 POI导入 首先拿到文…...

手把手教你做微信公众号
手把手教你做微信公众号 微信公众号可以通过注册的方式来建立。 1.进入微信公众平台 首先,在浏览器中搜索微信公众号,网页第一个就是,如下图所示,我们点进去。 2.注册微信平台账号 进入官网之后,如下图所示&#…...
python-在macOS上安装python库 xlwings失败的解决方式
问题:python库 xlwings安装失败 今天,看到网上有wlwings库,可以用来处理excel表格,立刻想试一试。结果,安装这个python库失败了。经过排查,问题解决。 安装过程和错误提示: 我用最简单直接的…...
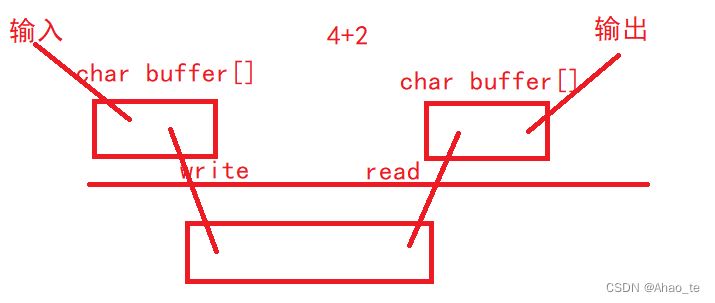
【Linux】进程间通信(匿名管道和命名管道通信、共享内存通信)
文章目录1、进程间通信1.1 进程的通信1.2 如何让进程间通信?1.3 进程间通信的本质2、管道通信2.1 匿名管道2.2 匿名管道通信2.3 命名管道2.4 命名管道的通信3、SystemV中的共享内存通信3.1 共享内存3.2 共享内存的通信3.3 共享内存的缺点以及数据保护3.4 共享内存的…...

漏洞分析: WSO2 API Manager 任意文件上传、远程代码执行漏洞
漏洞描述 某些WSO2产品允许不受限制地上传文件,从而执行远程代码。以WSO2 API Manager 为例,它是一个完全开源的 API 管理平台。它支持API设计,API发布,生命周期管理,应用程序开发,API安全性,速…...

详解Android 13种 Drawable的使用方法
前言关于自定义View,相信大家都已经很熟悉了。今天,我想分享一下关于自定义View中的一部分,就是自定义Drawable。Drawable 是可绘制对象的一个抽象类,相对比View来说,它更加的纯粹,只用来处理绘制的相关工作…...

MakeFile教程
前言 当我们需要编译一个比较大的项目时,编译命令会变得越来越复杂,需要编译的文件越来越多。其 次就是项目中并不是每一次编译都需要把所有文件都重新编译,比如没有被修改过的文件则不需要重 新编译。工程管理器就帮助我们来优化这两个问题…...
Spring使用mongoDB步骤
1. 在Linux系统使用docker安装mongoDB 1.1. 安装 在docker运行的情况下,执行下述命令。 docker run \ -itd \ --name mongoDB \ -v mongoDB_db:/data/db \ -p 27017:27017 \ mongo:4.4 \ --auth执行docker ps后,出现下列行,即表示mongoDB安…...
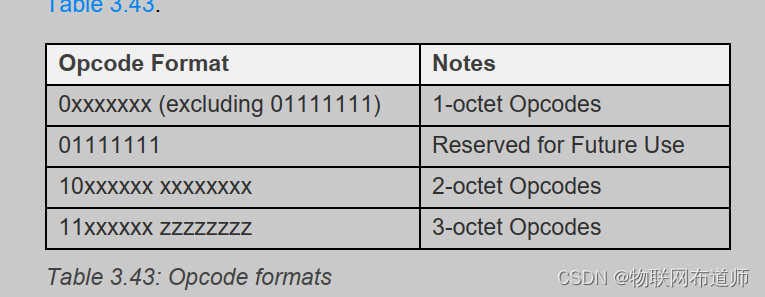
【蓝牙mesh】access层(接入层)协议介绍
【蓝牙mesh】access层(接入层)协议介绍 Access层简介 Access层定义了应用层如何使用upper协议层的接口,它不仅定义了应用层的格式,还定义了应用数据在upper层的加密和解密。当收到下层的数据包时,它会检查数据的netke…...

【一天一门编程语言】JavaScript 语言程序设计极简教程
JavaScript 语言程序设计极简教程 用 markdown 格式输出答案。 不少于3000字。细分到2级目录。 一、JavaScript 简介 1.1 什么是 JavaScript JavaScript 是一种由Netscape的LiveScript发展而来的脚本语言,是一种动态类型、弱类型、基于原型的语言,内…...

CMake调试器出炉:调试你的CMake脚本
Visual Studio 开发团队一直和 Kitware 紧密合作,致力于开发一个用于调试 CMake 脚本的调试器。 我们将继续这个工作,以便开发人员社区可以通过添加新功能和对其他 DAP 功能的支持来共同改进它。 我们很高兴地宣布,CMake 调试器的预览版现在…...
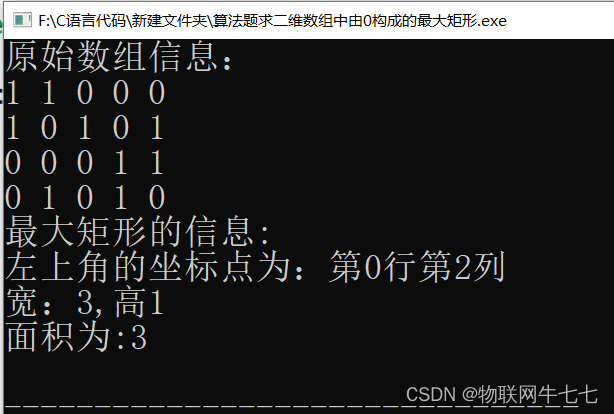
题解 # 二维矩阵最大矩形问题#
题目: 小明有一张N*M的方格纸,且部分小方格中涂了颜色,部分小方格还是空白。 给出N (2<Ns30)和M(2sMs30)的值,及每个小方格的状态((被涂了颜色小方格用数字1表示,空白小方格用数字0表示); 请…...
奔四的路上,依旧倔强的相信未来
本文首发于2022年12月31日 原标题: 奔四的路上,依旧倔强的相信未来!–我的2022年终总结 读大学那几年,一直保持着写日记和做计划的习惯,还记得大学毕业刚开始打工的时候,我的床头的墙上一定会画一张表,写上一个月的计划和一周的计划 计划也会有完不成的时候,但加深了…...

61 k8s + rancher + karmada容器化部署
文章目录 一、什么是rancher二、为什么使用rancher三、rancher安装1、细部介绍四、图形化操作1、执行2、补充五、 karmada1、官网2、细部介绍一、什么是rancher 1、Rancher 是一个 全栈式 的 Kubernetes 容器管理平台,为你提供在任何地方都能成功运行 Kubernetes 的工具。 二…...
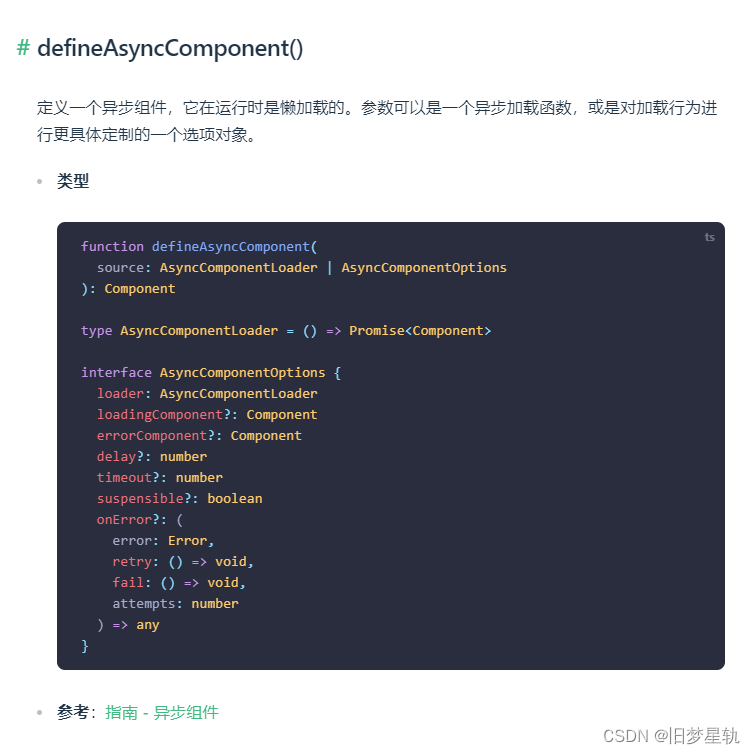
Vue3的新特性变化,上手指南!
文章目录一、Vue3相比Vue2,更新了什么变化?二、Proxy 代理响应式原理三、组合式 API (Composition API)setup()函数:ref()函数reactive()函数组合式 setup 中使用 Props 父向子传递参数计算属性watch(数据监视)watchEffect&#x…...
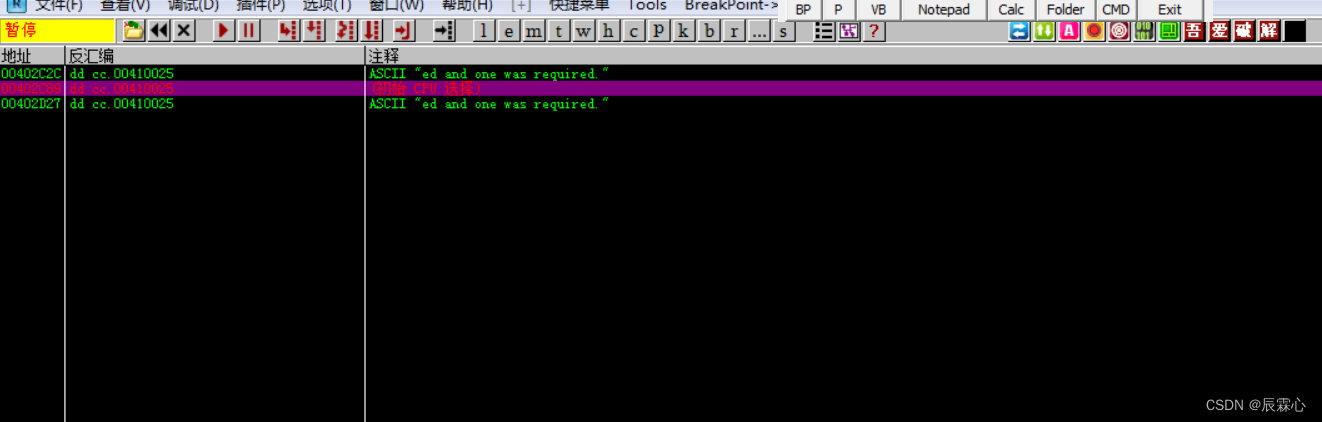
OllyDbg
本文通过吾爱破解论坛上提供的OllyDbg版本为例,讲解该软件的使用方法 F2对鼠标所处的位置打下断点,一般表现为鼠标所属地址位置背景变红F3加载一个可执行程序,进行调试分析,表现为弹出打开文件框F4执行程序到光标处F5缩小还原当前…...

记一次键盘维修,最终修复
我的笔记本是华硕的K45VD,是我亲人在高二那年买的,之后就一直给我用,距今2023年已经差不多13年,它承载了太多记忆。在大学期间也给它升级,重要的零部件基本没问题。只在大学时加了8G内存和一个240G固态,换了…...

LeetCode 155.最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。实现 MinStack 类:MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶部的元素。int getMin(…...

C++学习笔记-重载运算符和重载函数
重载的运算符是带有特殊名称的函数,函数名是由关键字 operator 和其后要重载的运算符符号构成的。与其他函数一样,重载运算符有一个返回类型和一个参数列表。 C 允许在同一作用域中的某个函数和运算符指定多个定义,分别称为函数重载和运算符重…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...
