leetcode_1155 掷骰子等于目标和的方法数
1. 题意
n个k面的骰子,投掷出骰子的点数之和为target的所有可能。
掷骰子等于目标和的方法数
2. 题解
动态规划,实际上相当于一个0-1背包。
令 d p [ i ] [ j ] dp[i][j] dp[i][j]为前 i i i个骰子和为j的方案数
则
d p [ i ] [ j ] = ∑ t = 1 k d p [ i − 1 ] [ j − t ] , j ≤ t dp[i][j] = \sum_{t=1}^{k}dp[i - 1][j -t], j \le t dp[i][j]=t=1∑kdp[i−1][j−t],j≤t
- 代码
class Solution {
public:int numRollsToTarget(int n, int k, int target) {// dp[i][j] = dp[i - 1][j - k] j - k >= i - 1int dp[30 + 1][1000 + 1];memset(dp, 0, sizeof(dp));int MOD = 1e9 + 7;dp[0][0] = 1;for (int i = 1;i <= n; ++i)for (int j = i + 1; j <= min(k * i, target); ++j) {for (int inc = 1; inc <= k; ++inc ) {if ( i - 1 <= j - inc )dp[i][j] = (dp[i][j] + dp[i - 1][j - inc] )% MOD;}}return dp[n][target];}
};
相关文章:

leetcode_1155 掷骰子等于目标和的方法数
1. 题意 n个k面的骰子,投掷出骰子的点数之和为target的所有可能。 掷骰子等于目标和的方法数 2. 题解 动态规划,实际上相当于一个0-1背包。 令 d p [ i ] [ j ] dp[i][j] dp[i][j]为前 i i i个骰子和为j的方案数 则 d p [ i ] [ j ] ∑ t 1 k d p…...

2023年中国精准放疗未来展望分析:将朝着精准化、数字化和智能化发展[图]
肿瘤放射治疗是利用放射线治疗肿瘤的一种局部治疗方法。放射线包括放射性同位素产生的α、β、γ射线和各类x射线治疗机或加速器产生的x射线、电子线、质子束及其他粒子束等。放射治疗在肿瘤治疗中的作用和地位日益突出,已成为治疗恶性肿瘤的主要手段之一。 现代放…...
)
大数据之LibrA数据库常见术语(二)
Cgroups Control Groups,控制组(FusionInsight LibrA中也称之为优先级组)。SUSE Linux和RedHat内核提供的一种可以限制、记录、隔离进程组所使用的物理资源的机制。 CLI Command-line Interface,命令行界面。应用程序和用户交互…...

华为面试题
一、实习 1、健康险核心 batch 自动查询和一键重启 2、后端如何实现免密登录 Spring Boot与Spring Security: 如果你使用的是Spring框架,Spring Security可以为你提供大量的安全功能。创建一个基于Spring Boot的新项目,并添加Spring Securi…...

进阶JAVA篇-深入了解 List 系列集合
目录 1.0 List 类的说明 1.1 List 类的常用方法 1.2 List 集合的遍历方式 2.0 ArrayList 集合的底层原理 2.1 从 ArrayList 集合的底层原理来了解具有该特性的原因: 2.2 ArrayList 集合的优缺点 3.0 LinkedList 集合的底层原理 3.1 从 LinkedList 集合的底层原理来了…...

typeof 与 instanceof 区别
typeof 和 instanceof 是 JavaScript 中用于检测数据类型的运算符,它们在使用和功能上有一些区别。 typeof 运算符: typeof 运算符用于检测给定值的数据类型,返回一个表示数据类型的字符串。typeof 可以用于检测基本数据类型(如字符串、数字、布尔值)和函数,也可以用于检…...

python 之计算矩阵乘法
文章目录 总的介绍例子 总的介绍 np.matmul 是NumPy库中的矩阵乘法函数,用于执行矩阵乘法操作。矩阵乘法是线性代数中的一种常见操作,用于将两个矩阵相乘以生成新的矩阵。在神经网络、机器学习和科学计算中,矩阵乘法经常用于变换和组合数据。…...
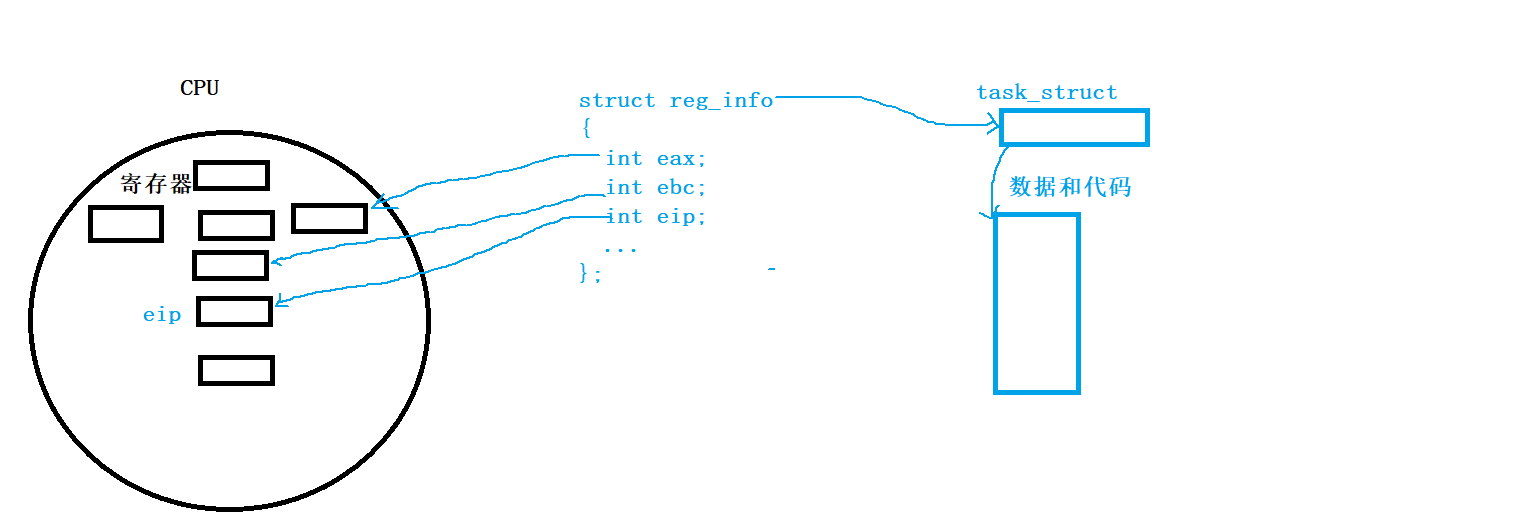
【Linux】进程优先级|进程并发概念|在vim中批量化注释
文章目录 前言tips——如何在vim中批量化注释进程更深度理解一、什么是进程优先级二、 为什么要有优先级三、Linux怎么设置优先级查看进程优先级的命令PRI and NI用top命令更改已存在进程的nice: 如何根据优先级开展调度呢?五、其他概念并发(…...

高效使用python之xlwt库编辑写入excel表内容
头条号:科雷软件测试 学习目录 了解下电脑中的excel表格文件格式 安装xlwt库 xlwt库写入表格内容 1 导入xlwt库 2 用一个图展示下xlwt常用的函数 3 往表格写入一些内容并保存 4 设置样式 1 先初始化XFStyle 2 设置字体font 3 设置边框 4 设置对齐方式 …...
【前端】Layui小功能收集整理
目录 1、layui 鼠标悬浮提示文字 2、关闭当前窗口并刷新父页面 3、子iframe关闭/传值/刷新父页面 1、layui 鼠标悬浮提示文字 鼠标放在图标上悬浮显示提示信息,效果图如下 <div style"float:left; line-height:40px">道试题 <i class"l…...
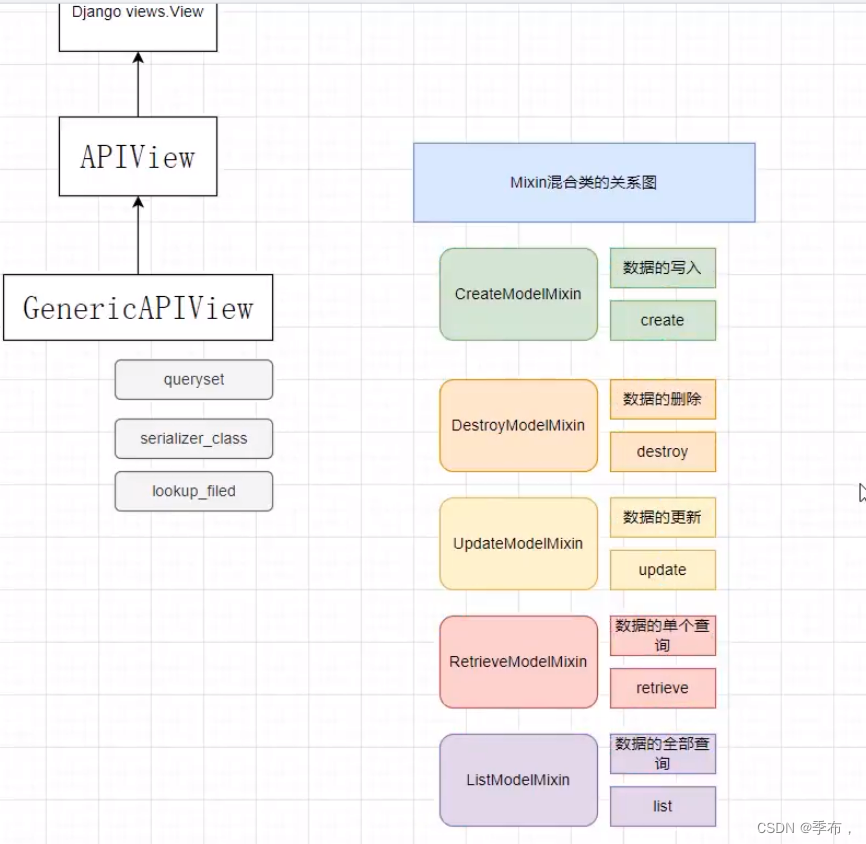
Django 地址接口开发
应用 Mixin 混合类进行收货地址接口开发 python ../manage.py startapp address继承了mixins扩展类,进到里面可以稍微看下源码 该方法帮我们实现了获取验证及保存的功能 address/views from rest_framework.generics import GenericAPIView from rest_framewo…...
.net6部署到linux上(CentOS Linux 7)
目录 一、先在linux上配置.net环境 添加 Microsoft 包存储库 安装 SDK 安装运行时 检查 SDK 版本可使用终端查看当前安装的 .NET SDK 版本。 打开终端并运行以下命令。 二、创建.net6 mvc项目 并发布 创建项目 修改默认端口 打包发布到文件夹 运行打包项目查看项目是否…...
docsify搭建个人博客——简单公共知识库
整站建设流程:安装docsify > 排错>配置封面> 配搜索> 启动> 放md类的文章> 自动生成目录; 更新文章流程: 把目录文章放到docsify\docs目录下,然后双击docsify-autosidebar.exe即可(它会重新生成目录…...
Ubuntu18.04如何安装搜狗、网易云音乐、百度网盘、金山WPS、谷歌浏览器、微信、Maven、Pycharm、Anaconda、MySQL8.0等软件
目录 1.搜狗输入法 下载 安装 卸载 2.网易云音乐 下载 安装 3.百度网盘 下载 安装 4.金山WPS 下载 安装 5.谷歌浏览器 下载 安装 6.微信 下载安装 7.Maven 下载 安装 配置镜像源 8.Pycharm 下载 安装 9.Anaconda 下载 安装 卸载 10.MySQL8.0 下载…...

【算法练习Day24】递增子序列全排列全排列 II
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 递增子序列容易出错的地方 …...

web3之链上情报平台Arkham
文章目录 web3之链上情报平台Arkham什么是Arkham链上情报交易所 Arkham Intel Exchange相较于传统情报交易方式,Arkham Intel Exchange下优势 web3之链上情报平台Arkham 什么是Arkham 官网:https://zh.arkhamintelligence.com/ 官方:https://platform.…...
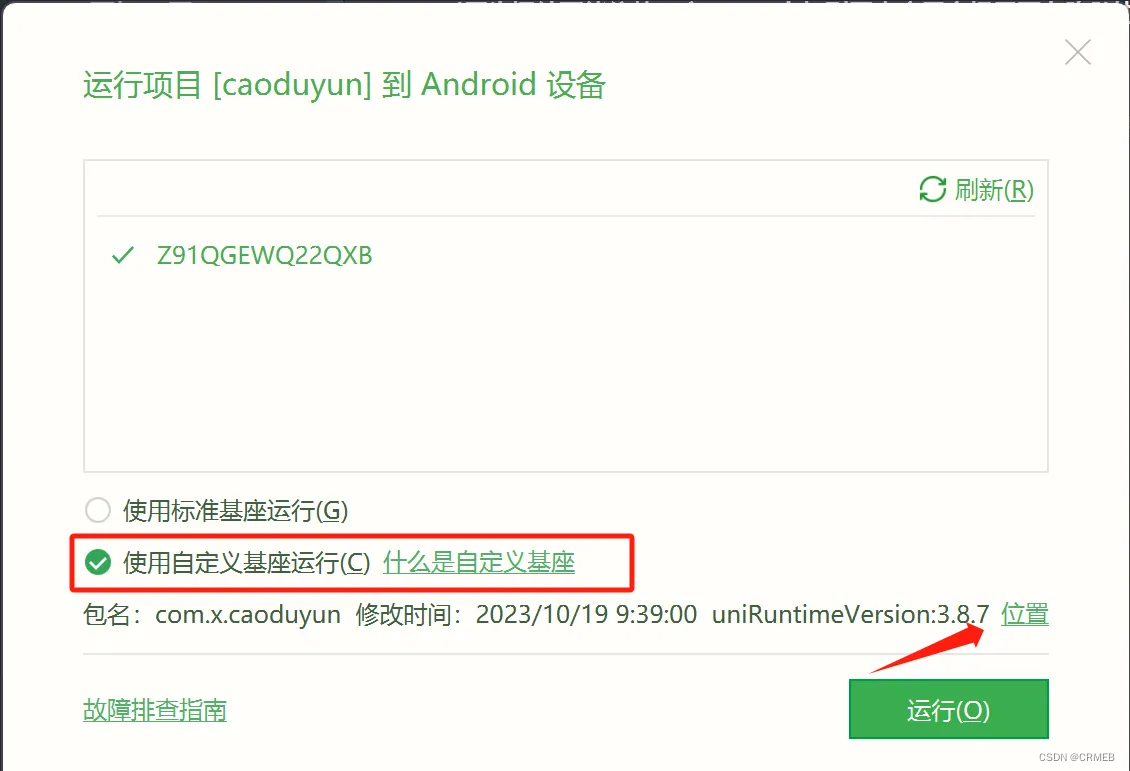
浅谈uniapp中开发安卓原生插件
其实官方文档介绍的比较清楚而且详细,但是有时候他太墨迹,你一下子找不到自己想要的,所以我总结了一下开发的提纲,也是为了自己方便下次使用。 1.第一步,下载官方提供的Android的示例工程,然后倒入UniPlugin-Hello-AS工程请在App离线SDK中查找,之后Android studio,编译运行项目…...

音频格式WAV
查找wav文件头关键struct 位置,当然也可查找avi文件头。用这个方法找到avi文件data位置后,可直接读出文件的每一帧图片。当然avi数据的标志位不是data,可以是00dc等。 WAV音频头文件有三个关键struct:RIFF, fmt,data。 AVI 视频文件头的关键…...

《语音优先》智能语音技术驱动的交互界面设计与语音机器人设计(译者序)...
“言为心声,语为心境”,语言与对话是我们沟通与协作的重要方式。而智能语音技术是一种基于人工智能和自然语言处理技术的语音交互技术。它可以通过语音识别技术将用户的语音指令转换为文本,然后通过自然语言处理技术对文本进行分析和理解,最终…...
[SQL开发笔记]WHERE子句 : 用于提取满足指定条件的记录
SELECT DISTINCT语句用户返回列表的唯一值:这是一个很特定的条件,假设我需要考虑很多中限制条件进行查询呢?这时我们就可以使用WHERE子句进行条件的限定 一、功能描述: WHERE子句用于提取满足指定条件的记录; 二、WH…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

linux设备重启后时间与网络时间不同步怎么解决?
linux设备重启后时间与网络时间不同步怎么解决? 设备只要一重启,时间又错了/偏了,明明刚刚对时还是对的! 这在物联网、嵌入式开发环境特别常见,尤其是开发板、树莓派、rk3588 这类设备。 解决方法: 加硬件…...

今日行情明日机会——20250609
上证指数放量上涨,接近3400点,个股涨多跌少。 深证放量上涨,但有个小上影线,相对上证走势更弱。 2025年6月9日涨停股主要行业方向分析(基于最新图片数据) 1. 医药(11家涨停) 代表标…...
)
Vue3学习(接口,泛型,自定义类型,v-for,props)
一,前言 继续学习 二,TS接口泛型自定义类型 1.接口 TypeScript 接口(Interface)是一种定义对象形状的强大工具,它可以描述对象必须包含的属性、方法和它们的类型。接口不会被编译成 JavaScript 代码,仅…...
