算法通关村第十一关青铜挑战——移位运算详解
大家好,我是怒码少年小码。
计算机到底是怎么处理数字的?
数字在计算机中的表示
机器数
一个数在计算机中的二进制表示形式,叫做这个数的机器数。
机器数是带符号的,在计算机用一个数的最高位存放符号,正数为0,负数为1。比如,十进制中的数+3,计算机字长为8位,转换成二进制就是00000011。如果是-3,就是10000011。这里的 00000011 和 10000011 都是机器数。
真值
将带符号位的机器数对应的真正数值称为机器数的真值。
例如上述-3的机器码10000011的真值是-3而不是131。(10000011换成十进制是131)
计算机对机器数的表示进一步细化:原码, 反码, 补码。
原码
第一位表示符号,其余位表示值。例如如果是八位二进制:
- [+1] 原 = 0000 0001
- [-1 ] 原 = 1000 0001
八位二进制有一位用于表示符号,所以原码的表示范围是[-127,127]。
反码
- 正数的反码是其本身
- 的反码是在其原码的基础上,符号位不变,其余各位取反。
- [+1] = [00000001]原 = [00000001]反
- [-1] = [10000001]原 = [11111110]反
补码
- 正数的补码就是其本身
- 负数的补码是在其原码的基础上你,符号位不变,其余各位取反,最后+1(也就是在反码的基础上+1)
- [+1] = [00000001]原 = [00000001]反 = [00000001]补
- [-1] = [10000001]原 = [11111110]反 = [11111111]补
看到这里你应该知道一个数在计算机中有三种编码方式。
拓展:反码、补码在人脑无法直观的看出来它的数值,那为啥还要有它们?
答:人脑可以知道第一位是符号位,在计算的时候我们会根据符号位选择对真值区域的加减。但是计算机要辨别"符号位"就必须获得全部的位的数据才可以,显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法。例如:根据运算法则减去一个正数等于加上一个负数。
1+(-1)=[00000001]反 + [11111110]反 = [11111111]反=[10000000]原 = -0
"0"的表示有点奇怪,+0和-0是一样的,而且0带符号是没有任何意义,而且要浪费[0000 0000]原和[10000000]原两个编码来表示0。于是补码的出现,解决了0的符号以及两个编码的问题:
1 + (-1) =[0000 0001]原 + [10000001]原= [00000001]补 + [1111 1111]补= [0000 0000]补=[0000 0000]原
[10000000]表示-128,所以补码的范围是[-128, 127]。(八进制中)
位运算规则
位运算主要有:与、或、异或、取反、左移和右移,其中左移和右移统称位移位运算,移位运算又分为算术移位和逻辑移位。
与
与运算的符号是&
运算规则:对于每个二进制位,当两个数对应的位都为1时,结果才为1,否则结果为0。
0 & 0 = 0
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1
或
或运算的符号是|
运算规则:对于每个二进制位,当两个数对应的位都为0时,结果才为0,否则结果为1
0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1
异或
异或运算的符号是⊕(代码表示是^)
运算规则:当两个数对应的位相同时,结果为0,否则结果为1
0 ⊕ 0 = 0
0 ⊕ 1 = 1
1 ⊕ 0 = 1
1 ⊕ 1 = 0
取反
取反运算的符号是~
运算规则:对一个数的每个二进制位进行取反操作,0变成1,1变成0
~0 = 1
~1 = 0
移位运算
移位运算按照移位方法分类可以分成左移和右移,按照是否带符号分类可以分成算术移位和逻辑移位
- 原始: 0000 0110 ===> 6
- 右移一次: 0000 0011 ===> 3 相当于除以2
- 左移一次: 0000 1100 ===> 12 相当于乘以2
左移运算的符号是<< ,左移运算时,将全部二进制位向左移动若干位,高位丢弃,低位补0。对于左移运算,算术移位和逻辑移位是相同的。
右移运算的符号是>>。右移运算时,将全部二进制位向右移动若干位,低位丢弃,高位的补位由算术移位或逻辑移位决定:
- 算术右移时,高位补最高位;
- 逻辑右移时,高位补0
- 示例1:29的二进制表示是0001 1101。 29左移2位的结果是116,对应的二进制是01110100;29左移3位的结果是-24,对应的二进制是11101000
- 示例2:-50的二进制表示是11001110(补码)。-50算术右移2位的结果是-13,对应的二进制表示是11110011;-50逻辑右移2位的结果是51,对应的二进制表示是00110011
拓展:计算机内部的右移运算采取的是哪一种?
答:
- 对于 C/C++ 而言,对于有符号类型,右移运算为算术右移;对于无符 号类型,右移运算为逻辑右移。
- 对于 Java 而言,不存在无符号类型,所有的表示整数的类型都是有符号类型,因此需要区分算术右移和逻辑右移。在Java中,算术右移的符号是>>,逻辑右移的符号是 >>>。
位运算常用技巧

位运算代码套路
获取
将 1 左移 i 位,得到形如 00010000 的值,接着堆这个值与num执行”位与“操作,从而将i位之外的所有位清零,最后检查该结果是否为零。不为零说明i位为1,否则i位为0。代码如下:
boolean getBit(int num,int i){return ((num&(1<<i))!=0);
}
设置
setBit先将1左移i位,得到形如00010000的值,接着堆这个值和num执行”位或“操作,这样只会改变i 位的数据。这样除i位外的位均为零,故不会影响num的其余位。代码如下:
int setBit(int num,int i){return num | (1 << i);
}
清零
与setBit相反,将1左移i位获得形如00010000的值,对这个值取反进而得到类似11101111的 值,接着对该值和num执行”位与“,故而不会影响到num的其余位,只会清零i位。
int clearBit(int num,int i){int mask = ~(1 << i);return num &mask;
}
更新
这个方法是将setBit和clearBit合二为一,首先用诸如11101111的值将num的第i位清零。接着将待写入 值v左移i位,得到一个i位为v但其余位都为0的数。最后对之前的结果执行”位或“操作,v为1这num的i 位更新为1,否则为0:
int updateBit(int num,int i,int v){int mask=~(1<<i);return (num&mask)|(v<<i);
}
END
说实话,更文到这里其实有点累了,学计算机也有点累了。网上负面消息一大堆,近几年就业形势不好,自己在学的东西也得不到正向反馈,有时候真的觉得自己挺废物的😔。或许看到这的小伙伴也和我有一样的想法,这里我想分享一段翁凯老师的话:
计算机的所有东西都是人做出来的,别人能想得出来的,你也一定能想得出来。在计算机里头没有任何黑魔法,所有的东西只不过是我现在不知道而已,总有一天我会把所有的细节、所有的内部的东西都搞明白了。
这贼船都上了,咱就好好走下去吧😁
相关文章:

算法通关村第十一关青铜挑战——移位运算详解
大家好,我是怒码少年小码。 计算机到底是怎么处理数字的? 数字在计算机中的表示 机器数 一个数在计算机中的二进制表示形式,叫做这个数的机器数。 机器数是带符号的,在计算机用一个数的最高位存放符号,正数为0&am…...

2023年面试测试工程师一般问什么问题?
面试和项目一起,是自学路上的两大拦路虎。面试测试工程师一般会被问什么问题,总结下来一般是下面这4类: 1.做好自我介绍 2.项目相关问题 3.技术相关问题 4.人事相关问题 接下来,主要从以上四个方向分别展开介绍。为了让大家更有获…...
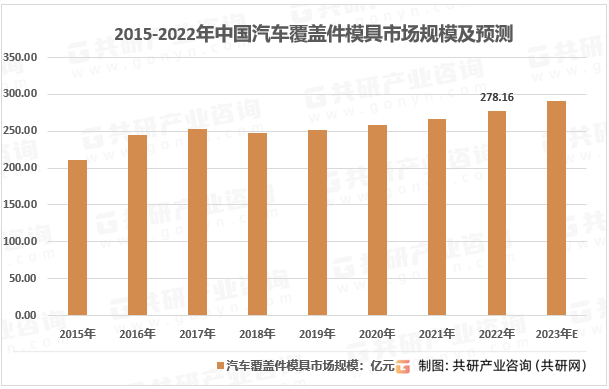
2023年中国汽车覆盖件模具竞争格局、市场规模及行业需求前景[图]
汽车覆盖件模具是汽车车身生产的重要工艺装备,其设计和制造时间约占汽车开发周期的 2/3,是汽车换型的重要制约因素之一。汽车覆盖件模具具有尺寸大、工作型面复杂、技术标准高等特点,属于技术密集型产品。汽车覆盖件模具按以其冲压的汽车覆盖…...
vue3项目运行报错import zhCn from “element-plus/lib/locale/lang/zh-cn“
解决办法 import zhCn from "element-plus/lib/locale/lang/zh-cn";修改为 import zhCn from "element-plus/dist/locale/zh-cn.mjs";...
、条款27(禁止部分隐式生成的函数))
读书笔记:Effective C++ 2.0 版,条款26(歧义)、条款27(禁止部分隐式生成的函数)
条款26: 当心潜在的歧义 即使cpp支持潜在二义性/歧义,也不要使用。 void f(int); void f(char); double d 6.02; f(d); //需要明确转换多继承充满了潜在二义性/歧义的可能。 class Base1 {public: int doIt();}; class Base2 {public: void doIt();}; class Deri…...

MySQL基本操作之数据库设计理论
1、数据的设计准则 1)糟糕的数据库设计表现在以下几个方面: 访问数据效率低下存在大量的数据冗余,浪费存储空间更新和检索数据时会出现许多问题2)良好的数据库设计表现在以下几方面: 访问效率高减少数据冗余,节省存储空间便于进一步扩展可以使应用程序的开发变得更容易…...
)
SpringBoot的日志系统(日志分组、文件输出、滚动归档)
[toc](目录) > SpringBoot3需要jdk17 # 1. 简介 1. Spring5及以后Spring自己实现了commons-logging,来作为内部的日志。日志的jar包是org.springframework:spring-jcl:6.0.10。查看org.apache.commons.logging.LogAdapter Java package org.apache.commons.log…...
一种基于HTTPS实现的Web账号登录Linux桌面系统的实现方案
问题由来 客户需求计划列入支持第三方帐号系统,包括Web账号。需求来源是用户想要用它们的帐号直接登录Linux Deepin操作系统。一个失败的实现方案是用户以较小的成本改造帐号管理系统发布HTTP服务,我们开发一个PAM模块与Web服务器交互,数据格…...

【Linux】psplash制作Linux开机动画
1. 下载psplash软件 下载psplash源码到ubuntu中: 下载地址:https://git.yoctoproject.org/psplash/commit/安装依赖环境 sudo apt-get install libgdk-pixbuf2.0-dev2. 准备图片 开机动画静态图片:psplash-poky.png开机动画进度条图片&…...

WMS透明仓库:实现仓储的全方位可视化与优化
一、WMS透明仓库的定义与特点 1. WMS透明仓库的定义:WMS透明仓库是一种基于信息技术的仓库管理系统,通过实时数据采集、分析和可视化,将仓库内外的物流流程、库存状态、人员活动等信息以透明的方式展示给相关利益方。 2. 实时数据采集&…...

软考系统架构师知识点集锦一:系统工程与信息系统基础
一、考情分析 二、考点精讲 2.1 软件开发方法 (1)结构化开发方法 用户至上,自顶向下,逐步分解(求解),严格区分工作阶段,每阶段有任务与成果,强调系统开发过程的整体性和全局性,系统开发过程工…...

建筑模板常见的问题有哪些?
在建筑模板的使用过程中,常见的问题包括以下几个方面:1. 模板质量问题: - 模板破损或变形:模板可能在运输、安装或使用过程中受到损坏,如裂缝、断裂或变形。这可能导致模板的稳定性和承载能力下降。 - 模板尺寸不准确&…...
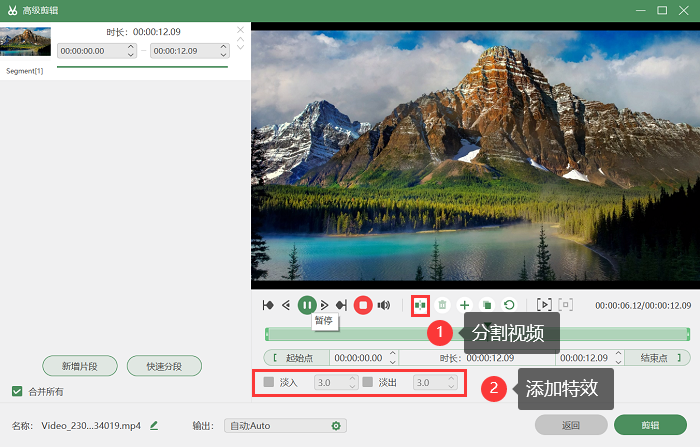
windows11录屏功能详解,记录你的精彩时刻
windows 11是微软最新推出的操作系统版本,拥有很多简单便捷的功能,包括内置的录屏工具,让用户可以轻松地录制屏幕内容。但是很多人不了解windows11录屏功能,本文将详细介绍windows 11录屏的三个方法,以及它们的优势和适…...

重入漏洞Victim
重入漏洞 顾名思义,重入漏洞可以简单理解为“重新进入的漏洞”。举个简单的例子,你往某个合约里存入了1个Ether,然后点击退款,按理来说只能退一个Ether,但是可以利用重入漏洞反复退款,把合约里的Ether掏空…...

wordpress数据库迁移Invalid default value for ‘comment_date‘
问题说明 最近在往新的电脑上迁移一个wordpress网站,在往新电脑上的mysql数据库中导入数据时,报错:1067 - Invalid default value for comment_date。 异常分析 这个错误的字面意思就是字段‘comment_date’的默认值是无效的,于…...
Xray联动RAD实现自动扫描教程
Rad下载地址:https://github.com/chaitin/rad xray下载地址:https://github.com/chaitin/xray Xray启动监听: xray_windows_amd64.exe webscan --listen 127.0.0.1:7777 --html-output xray-xxx.html RAD启动爬虫抓包: rad_win…...

ES6 Proxy
定义: Proxy 可以理解成,在目标对象之前架设一层“拦截”,外界对该对象的访问,都必须先通过这层拦截,因此提供了一种机制,可以对外界的访问进行过滤和改写。Proxy 这个词的原意是代理,用在这里表…...
:重新思考CNN大核注意力设计)
LSKA(大可分离核注意力):重新思考CNN大核注意力设计
文章目录 摘要1、简介2、相关工作3、方法4、实验5、消融研究6、与最先进方法的比较7、ViTs和CNNs的鲁棒性评估基准比较8、结论摘要 https://arxiv.org/pdf/2309.01439.pdf 大型可分离核注意力(LSKA)模块的视觉注意力网络(VAN)已被证明在各种基于视觉的任务上提供了卓越的性…...

muduo源码学习base——Exception(带 stack trace 的异常基类)
Exception(带 stack trace 的异常基类) 前置ExceptionCurrentThread::stackTrace() 前置 ABI: Application Binary Interface,应用程序二进制接口,可以参考:细谈ABI RTTI type_info: RTTI:Run Time Type Identificatio…...

2023-10-24 小总结
起始 不知不觉,作为职业码农,已经过去了4年。第4个1024了。 期间和Java、C#、JavaScript都打过交道。他们都很优秀。自然,好刀要在强者手中才能熠熠生辉。 快30了,回首过去,很感慨。发生了很多事,很多我都…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
