内存分段、分页
大家好,我叫徐锦桐,个人博客地址为www.xujintong.com。平时记录一下学习计算机过程中获取的知识,还有日常折腾的经验,欢迎大家访问。
前言
每个进程都有一套自己的虚拟地址,尽管进程可能有相同的虚拟地址,但经过映射后就是不同的物理地址了,以此来实现进程隔离等功能。
内存分段
介绍
一开始使用分段来进行内存管理的,但是用多了会发现,使用分段管理会产生大量的外部碎片。
说到分段,肯定要讲到GDT(全局描述符表) 和 段选择子 还有段描述符。
简单来说,它们之间的关系就是GDT是一个数组,里面存着段描述符,通过段选择子(索引)找到对应的段描述符。
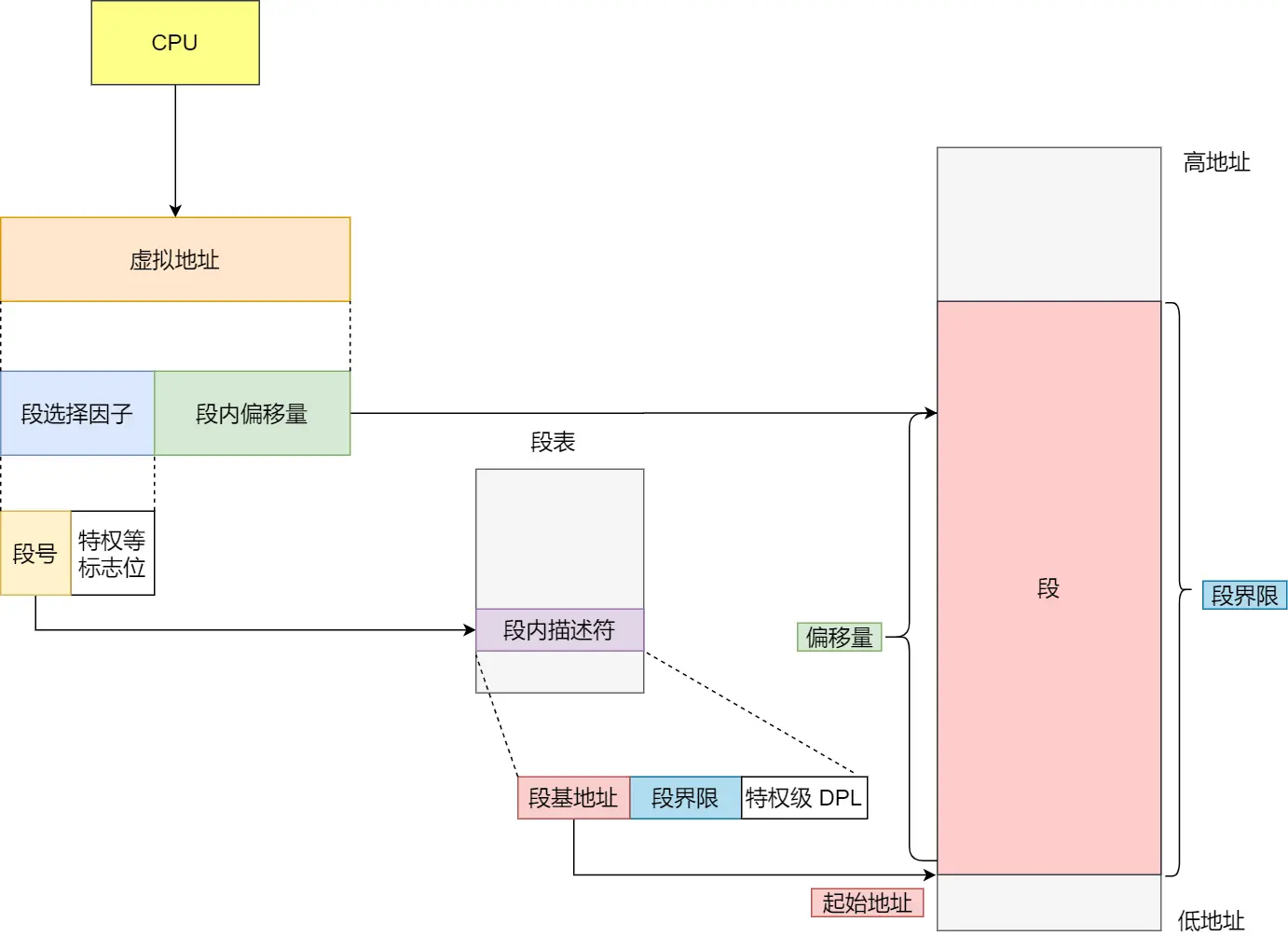
具体的寻址方式就是,虚拟地址=段选择子+段内偏移量。
通过段选择子找到在GDT表中找到对应的段描述符,然后就是判断特权级,特权级允许后找到对应的段基址,然后再加上偏移量就是对应的物理地址了。
段描述符的结构如下图:
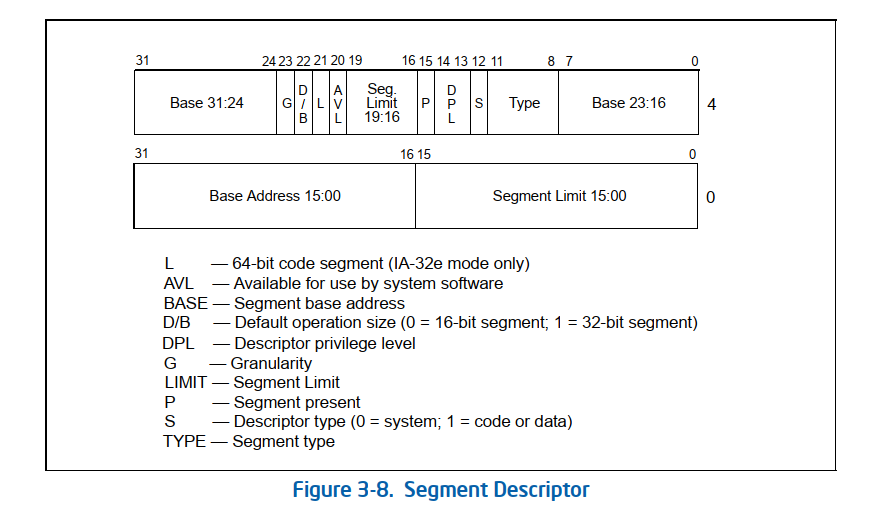
在进程中,我们一般将进程的TSS描述符(一种特殊的段描述符,里面存着进程的数据段、代码段等段的位置和进程运行所需所有的寄存器的值,和进程特权级等) 作为段内描述符,当进行任务切换的时候,系统加载进程对应的TSS结构来恢复进程。
// 这是我做过的一个极简版32位操作系统中的代码
// 项目地址:https://github.com/xjintong/SimilarLinux0.11
typedef struct _tss_t {uint32_t pre_link; uint32_t esp0, ss0, esp1, ss1, esp2, ss2;uint32_t cr3;uint32_t eip, eflags, eax, ecx, edx, ebx, esp, ebp, esi, edi;uint32_t es, cs, ss, ds, fs, gs;uint32_t ldt; uint32_t iomap;
}tss_t;
不足
分段会产生两个问题。
- 外部内存碎片
分段会产生外部内存碎片。就是因为段的长度是不固定的,对于内存的分配有可能不是很合理,就比如说下面,空闲内存大于新进程的内存,但是由于两个空闲内存是分开的,导致新进程不能加载到内存中。
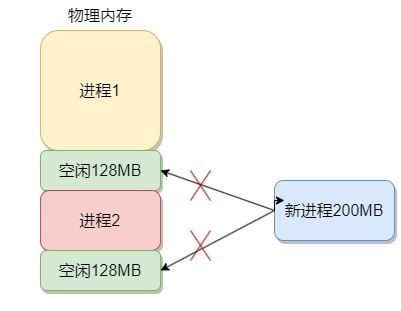
解决这个问题的方法就是内存交换。
也就是先将进程2放到磁盘中去,然后把新进程放到内存中(挨着进程1放),然后再把磁盘中的进程2重新读取到内存,这个在磁盘上和内存进行数据交换的空间就是swap空间。
- 内存交换率低
磁盘读写数据相对内存来说是非常慢的,如果是一个内存占用非常大的进程要从内从交换到磁盘,所消耗的时间是非常大的。
内存分页
一级页表
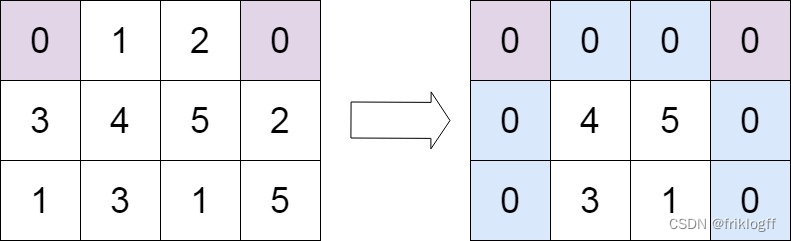
我们可以将所有的物理内存和虚拟均匀分成等份的(一般就是4KB)页,然后创建一个表,里面存储着虚拟页和物理页的映射关系,到时候就直接查表,找到对应的物理页,最后再加上页偏移就是物理地址了。
一级页表的起始位置放在CR3寄存器中。
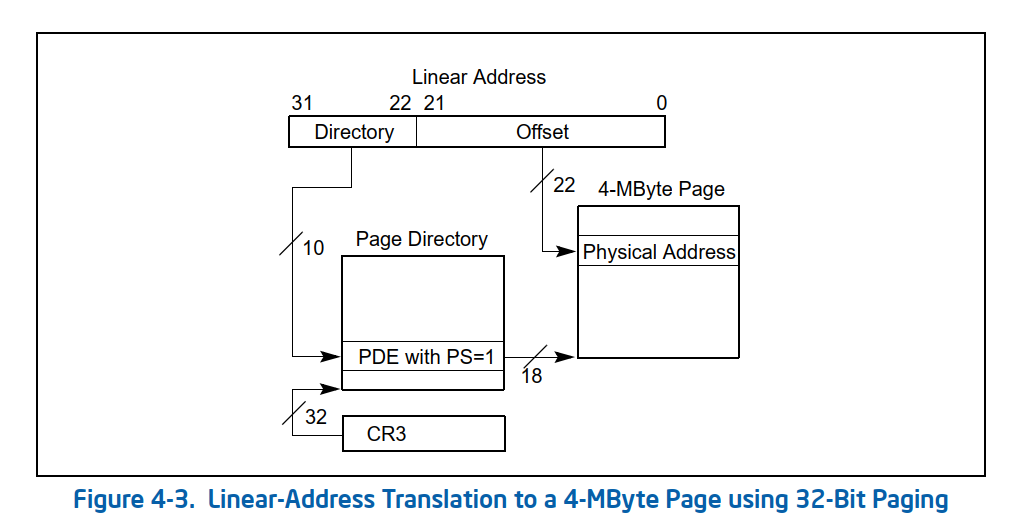
采用分页很好的解决了外部内存碎片化和内存交换率低的问题。但是如果只用一级页表,还是有着很大的问题。
我们以32位操作系统为例,内存总共4GB(2^32) ,一个页4KB(212),那么就需要百万级(220)的映射关系,一个页表项需要4字节存储,然后所有的表项就需要4MB(2^22)内存存储。
看着不是很多吧,但是每个进程都需要一个这样的表,如果进程变多了,这得多消耗多少没必要消耗的空间。
而且我们必须有这个表的全部,因为是靠索引来找到对应的页的,你如果只取一部分那它的索引号就变了。所以我们需要多级页表来解决这个问题。
多级页表
32位操作系统用二级页表就够了,64位操作系统用四级页表,这里只讲32位的。
我们先把内存分成1024(2^10)个大的页目录,一个页目录指向一个页表(一个页表含有1024个页目录),
第一级是页目录(page directory),一共1024(210)个目录项,一个目录项4字节大小,所以页目录占4KB(222)大小内存。
第二级是页表(page table),它也是1024(2^10)个页表项,一个页表也是4KB大小。一个页表的最大寻址空间是4MB(因为1024个页表项,对应1024个页物理地址,一个页物理地址是4KB)。
一个目录项对应着一个页表,所以一个目录项最大寻址4MB,一个目录有1024个目录项,所以一个目录最大寻址4GB。
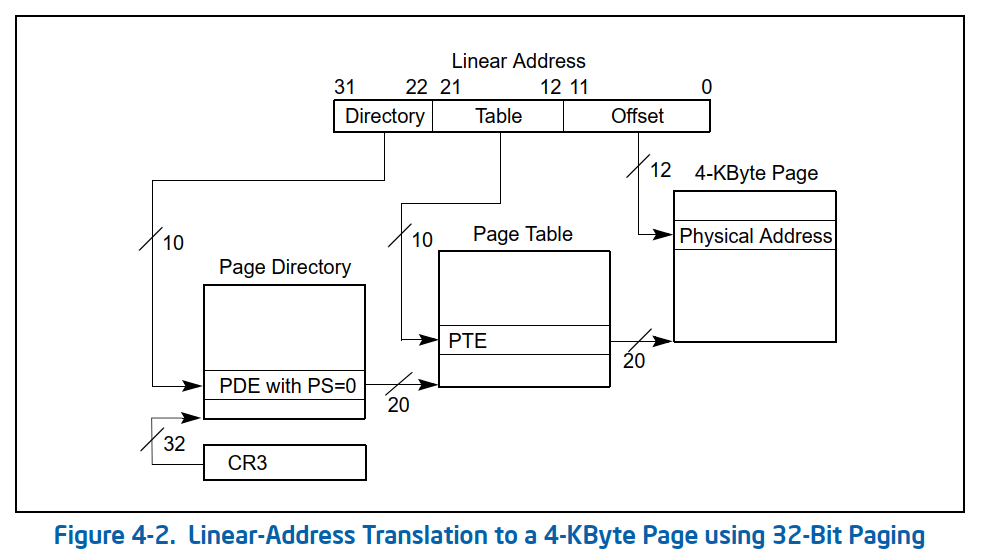
虚拟地址的高10位是页目录索引,中间10位是页表索引,最后12位是偏移量。
页目录的结构和页表的结构是一样的,只不过他俩描述的主体不一样,一个描述的是页目录,一个描述的是页表。
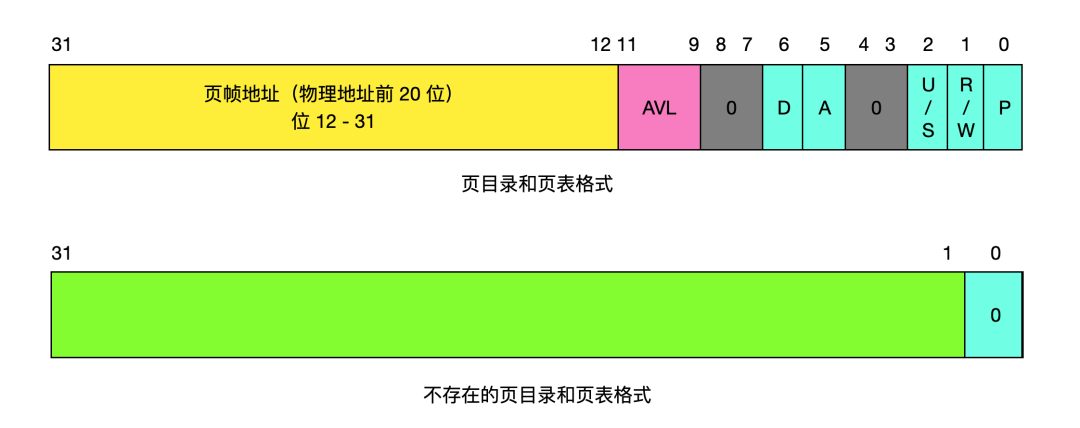
通过页目录和页表可以获取物理地址的前20位,后12位就是加上虚拟地址的后12位。虚拟地址的后12位存储的权限,读写标志等等。
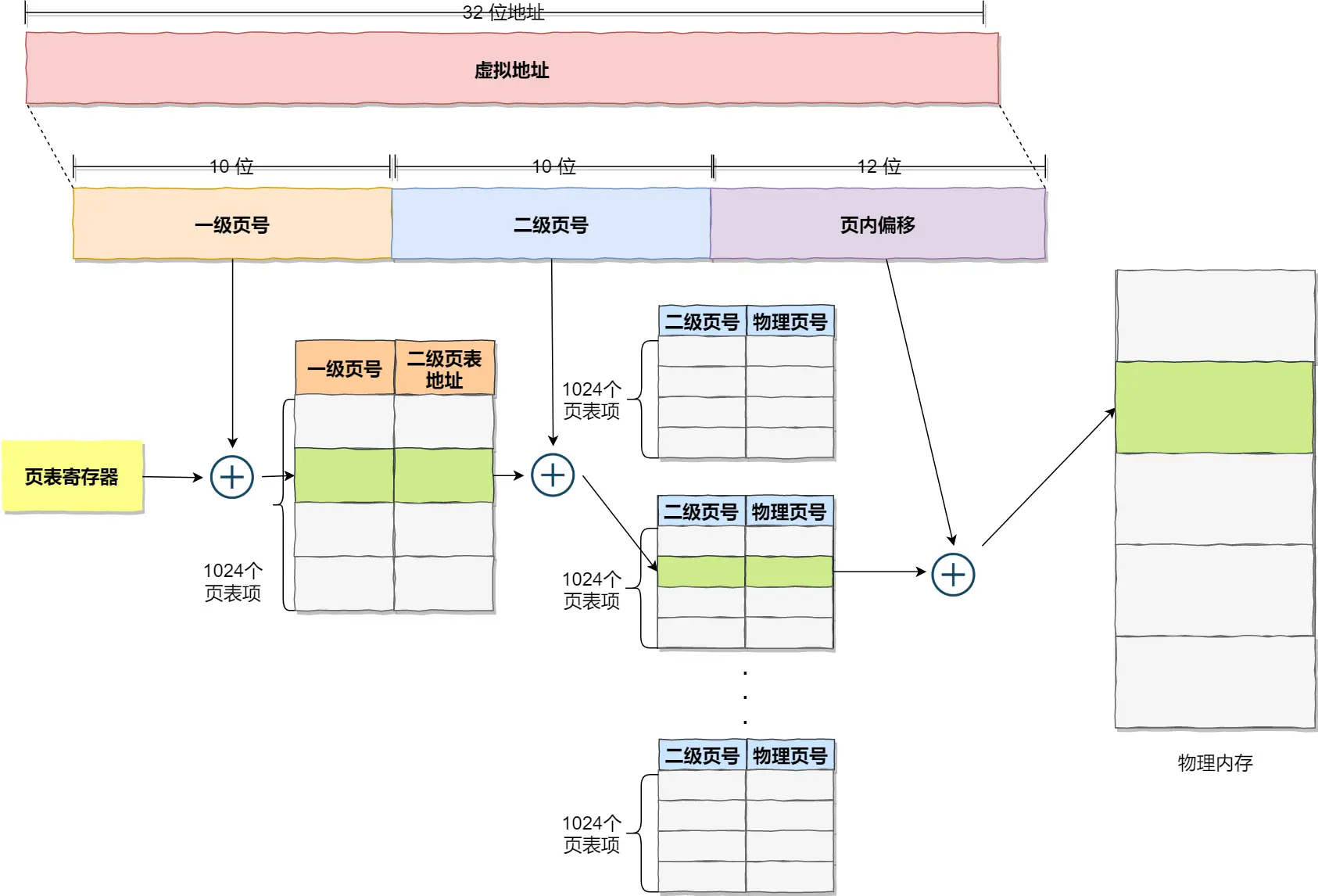
通过二级页表我们不用保存所有的映射关系了。有一个页目录就能扫完4GB内存,然后再找对应的页表,如果没有就再创建。如果某个一级页表的页表项没有被用到,也就不需要创建这个页表项对应的二级页表了,即可以在需要时才创建二级页表
就像下面这样二级表有1024个,每个二级表有1024个表项并且索引都是从0开始的,这样我们单独拿出一个二级表,它的索引也不会变化。由于局部性原理,我们用不到那么多的页表项。
TLB
从虚拟地址到物理地址的转换还需要查两次表,64位的还要查4次,时间也是有消耗的。TLB里面保存了一些之前已经转换好的虚拟地址和物理地址的映射关系。
详细的请看我写的另一篇文章
Linux内存布局
inter处理器早期是用分段管理内存,后来发现不是很好用,后来又整了分页,但是还保留着分段,就是虚拟地址是通过分段获取的,然后再通过分页。
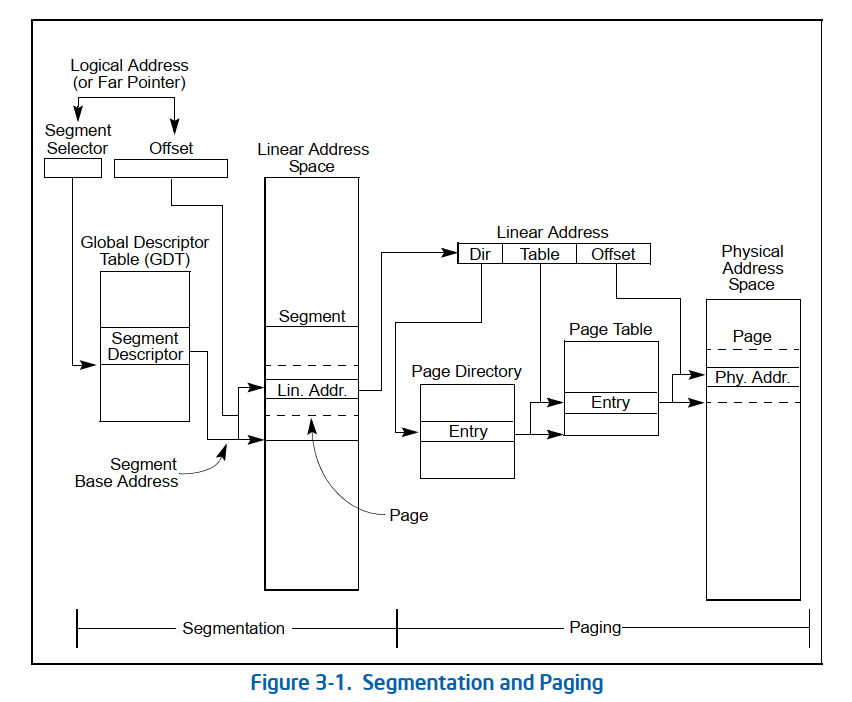
可以看到最左边还有分段的,是通过分段获取的线性地址。
但是分段确实有点弊端,Linux无法改变硬件,只能改变自身了。Linux用了一个技巧使分段相当于失效了。
Linux 系统中的每个段都是从 0 地址开始的整个 4GB 虚拟空间(32 位环境下),也就是所有的段的起始地址都是一样的。这意味着,Linux 系统中的代码,包括操作系统本身的代码和应用程序代码,所面对的地址空间都是线性地址空间(虚拟地址),这种做法相当于屏蔽了处理器中的逻辑地址概念,段只被用于访问控制和内存保护。
Linux的地址空间分为内核空间和用户空间。
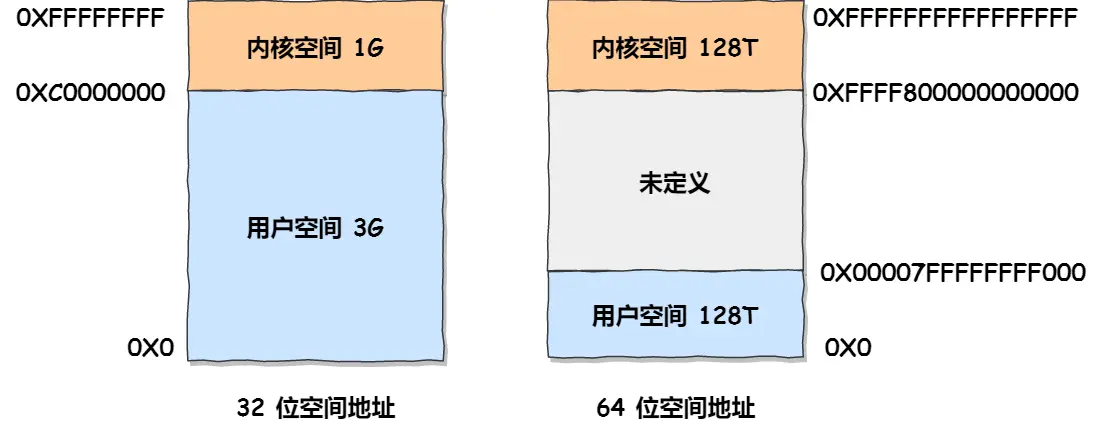
在内核空间是不开启分页机制的,所有进程共享内核内存。有人认为这是为了防止从用户态到内核态的性能消耗。
最后
每个进程都有完全属于自己的地址转换表,所以即便是相同的虚拟地址空间也会映射到不同的物理地址上,以此来达到隔离进程的效果。
在进程看来,自己是独享整个内存,自己可以随便找个地址,但其实是通过页表映射到个各个物理上。
- 参考博客
小林coding–为什么要有虚拟内存
图文详解 Linux 分页机制!
MIT6.S081 4.3 页表(Page Table)
相关文章:

内存分段、分页
大家好,我叫徐锦桐,个人博客地址为www.xujintong.com。平时记录一下学习计算机过程中获取的知识,还有日常折腾的经验,欢迎大家访问。 前言 每个进程都有一套自己的虚拟地址,尽管进程可能有相同的虚拟地址,…...
Python-pptx教程之一从零开始生成PPT文件
简介 python-pptx是一个用于创建、读取和更新PowerPoint(.pptx)文件的python库。 典型的用途是根据动态内容(如数据库查询、分析数据等),将这些内容自动化生成PowerPoint演示文稿,将数据可视化,…...
k8s 使用ingress-nginx访问集群内部应用
k8s搭建和部署应用完成后,可以通过NodePort,Loadbalancer,Ingress方式将应用端口暴露到集群外部,提供外部访问。 缺点: NodePort占用端口,大量暴露端口非常不安全,并且有端口数量限制【不推荐】…...

企业数据泄露怎么办?
随着数字化时代的到来,威胁企业数据安全的因素越来越多。一旦机密数据泄露,不仅会对企业造成巨大的经济损失,还会对企业的声誉和客户信任度造成严重影响。发生数据泄露情况时,企业该怎样应对? 1.确认数据泄露 确认是…...
GoLong的学习之路(一)语法之变量与常量
目录 GoLang变量批量声明变量的初始化类型推导短变量声明匿名变量 常量iota(特殊)(需要重点记忆) GoLang go的诞生为了解决在21世纪多核和网络化环境越来越复杂的变成问题而发明的Go语言。 go语言是从Ken Thomepson发明的B语言和…...
Go-Python-Java-C-LeetCode高分解法-第十一周合集
前言 本题解Go语言部分基于 LeetCode-Go 其他部分基于本人实践学习 个人题解GitHub连接:LeetCode-Go-Python-Java-C 欢迎订阅CSDN专栏,每日一题,和博主一起进步 LeetCode专栏 我搜集到了50道精选题,适合速成概览大部分常用算法 突…...

封装axios的两种方式
作为前端工程师,经常需要对axios进行封装以满足复用的目的。在不同的前端项目中使用相同的axios封装有利于保持一致性,有利于数据之间的传递和处理。本文提供两种对axios进行封装的思路。 1. 将请求方式作为调用参数传递进来 首先导入了axios, AxiosIn…...

【自然语言处理】NLTK库的概念和作用
文章目录 一、NLTK库介绍二、NLTK库的使用2.1 初级使用2.2 中级使用 参考资料 一、NLTK库介绍 Natural Language Toolkit (NLTK)是一个广泛使用的Python自然语言处理工具库,由Steven Bird、Edward Loper和Ewan Klein于2001年发起开发。NLTK的目的是为自然语言处理&…...

Python爬虫如何解决提交参数js加密
注意!!!! 仅做知识储备莫拿去违法乱纪,有问题指出来,纯做笔记记录 由于¥%…………&&%#%** 所以!#¥……&*……* 啥也不说直接上代码 import execjs js_ji…...
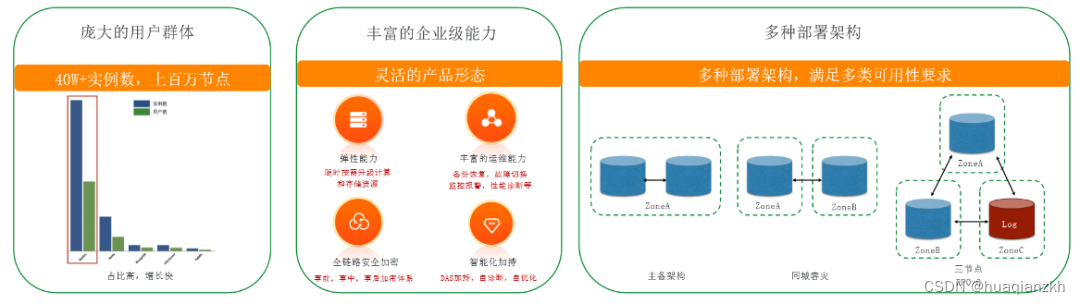
云数据库及RDS数据库介绍
1.云数据库概念 云数据库是指被优化或部署到一个虚拟计算环境中的数据库,具有按需付费、按需扩展、高可用性以及存储整合等能力。 2.云数据库特性 云数据库的特性有:实例创建快速、支持只读实例、读写分离、故障自动切换、数据备份、Binlog备份、SQL审…...

c语言进阶部分详解(详细解析自定义类型——枚举,联合(共用体))
上篇文章介绍了结构体相关的内容,大家可以点击链接进行浏览:c语言进阶部分详解(详细解析自定义类型——结构体,内存对齐,位段)-CSDN博客 各种源码大家可以去我的gitee主页进行查找:唔姆 (Nerow…...

使用 Requests 库和 PHP 的下载
以下是一个使用 Requests 库和 PHP 的下载器程序,用于从 www.people.com.cn 下载音频。此程序使用了 https://www.duoip.cn/get_proxy 这段代码。 import requests from bs4 import BeautifulSoup import pafy import timedef get_proxy():url "https://www.…...
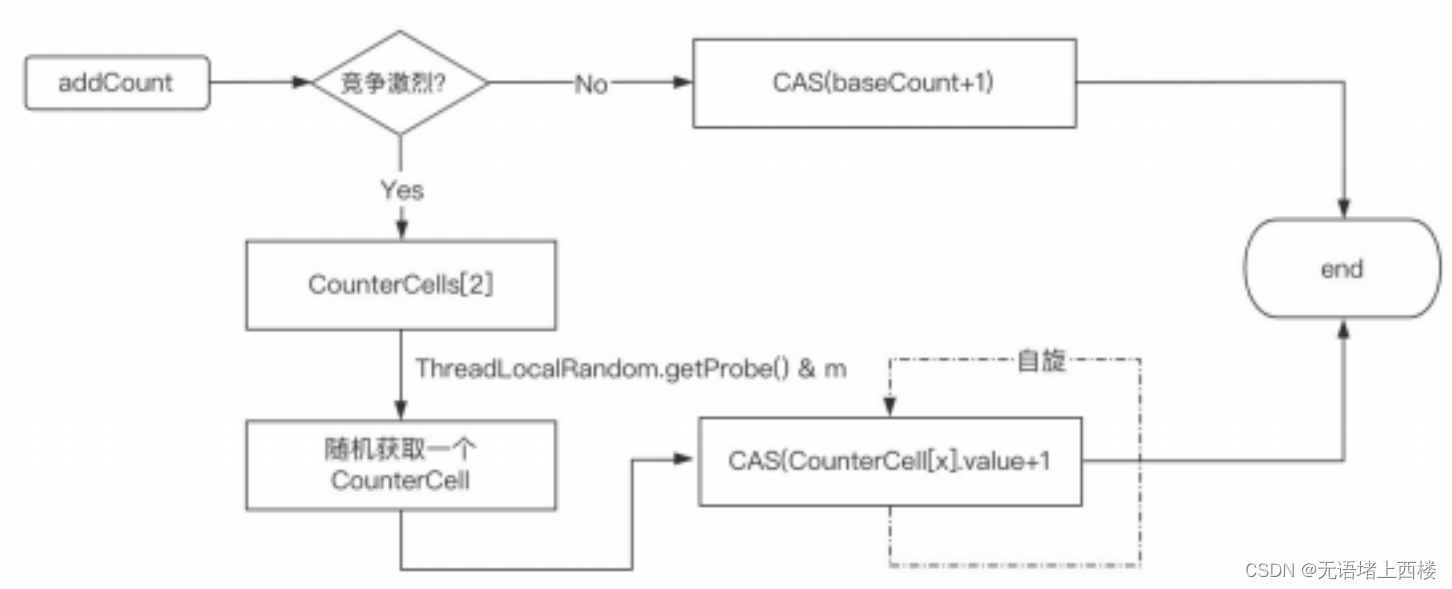
ConcurrentHashMap底层具体实现知道吗?实现原理是什么
从这三个方面来回答: ConcurrentHashMap 的整体架构 ConcurrentHashMap 的基本功能 ConcurrentHashMap 在性能方面的优化 ConcurrentHashMap 的整体架构 这个是 ConcurrentHashMap 在 JDK1.8 中的存储结构,它是由数组、单向链表、红黑树组成. 当我们初始…...

Go语言“Go语言:掌握未来编程的利器“
Go语音的发展史可以追溯到2009年,当时谷歌公司推出了一款名为“Google Assistant”的智能助手,它使用自然语言处理技术来与用户进行交互。随后,Go语音逐渐发展成为一种广泛使用的语音技术,其发展历程如下: 起步阶段&a…...

达梦管理工具报错“结果集不可更新,请确认查询列是否出自同一张表,并且包含值唯一的列。”
在使用达梦数据库管理工具时,我们测试过程中时常需要更新表数据,有时为了便捷,会直接使用管理工具修改表数据的值,但偶尔会遇到“结果集不可更新,请确认查询列是否出自同一张表,并且包含值唯一的列。”的报…...
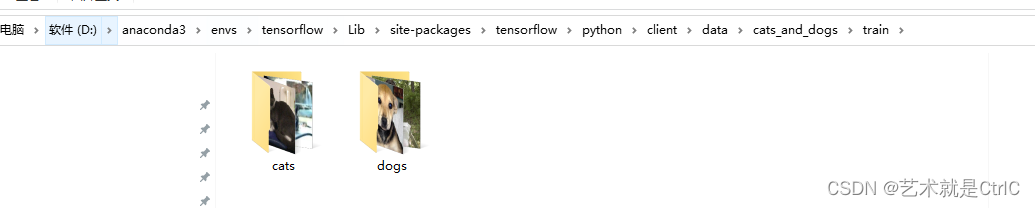
TensorFlow2从磁盘读取图片数据集的示例(tf.keras.utils.image_dataset_from_directory)
import os import warnings warnings.filterwarnings("ignore") import tensorflow as tf from tensorflow.keras.optimizers import Adam from tensorflow.keras.applications.resnet import ResNet50#数据所在文件夹 base_dir ./data/cats_and_dogs train_dir os…...

Unity开发过程中的一些小知识点
1、如何查询挂载了指定脚本的游戏物体 可以直接在Hierarchy面板上,搜索想要找的脚本名 2、如何将Unity生成的多个相同游戏物体获得序号 可以使用Unity的API Transform.GetSiblingIndex() 实现。 Transform.GetSiblingIndex()gameobject.idTransform.GetSiblingI…...
大语言模型(LLM)综述(一):大语言模型介绍
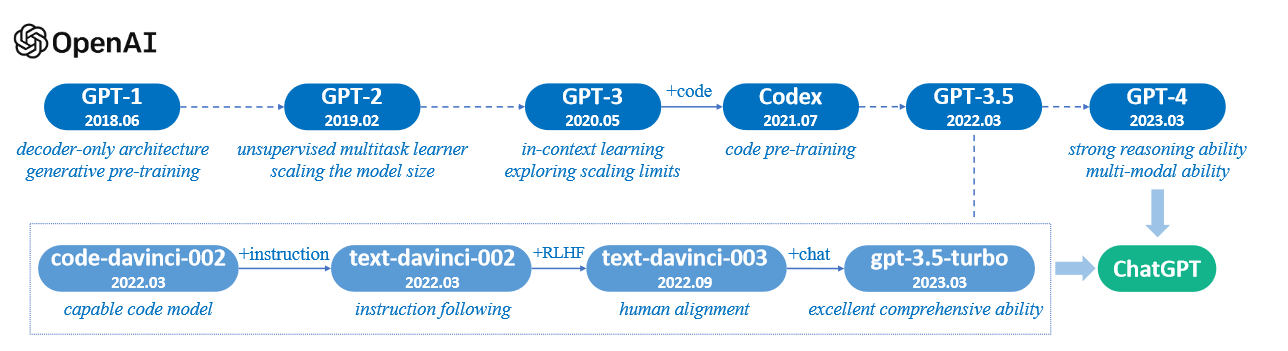
A Survey of Large Language Models 前言1. INTRODUCTION2. OVERVIEW2.1 大语言模型的背景2.2 GPT系列模型的技术演变 前言 随着人工智能和机器学习领域的迅速发展,语言模型已经从简单的词袋模型(Bag-of-Words)和N-gram模型演变为更为复杂和…...

在Ubuntu上安装和挂载NFS
在Ubuntu上安装和挂载NFS可以按照以下步骤进行: 安装NFS客户端工具:在Ubuntu上,可以使用以下命令安装NFS客户端工具: shell复制代码 sudo apt-get install nfs-common 创建挂载点:在本地Ubuntu计算机上,…...
)
Python 实现的简易数据库管理系统 (DBMS)
在这篇文章中,我们将深入探讨如何使用 Python 从头开始实现一个简易的数据库管理系统 (DBMS)。这不是一个生产级的 DBMS,但它为我们提供了一个如何构建数据库系统的基础概念。 1. 数据表的实现 首先,我们定义了一个 Table 类来模拟数据库中…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
