20231023 比赛总结
比赛链接
反思
A
花了很长时间,幸亏没怎么调就对了,以后还是应该先看其他题的
括号匹配题的套路感觉没有掌握透,感觉无非就是单调栈,哈希,折线图
B
感觉比 T 1 T1 T1 简单
C
正解还是很妙的,但 68 p t s 68pts 68pts 的线段树优化建图很好拿(但不太好写)
D
感觉并不是那么难,用 d p dp dp 化简多项式还是第一次见到
题解
A
考虑每个右括号只会匹配一个左括号,于是我们可以进行类似 d p dp dp 的操作,我们记录每段区间的 d p dp dp 值,可以发现每段区间只会有一个位置的 d p dp dp 值 > 1 >1 >1,其他都 = 1 =1 =1,所以直接用单调栈维护即可
有些细节需要仔细想一下,也说不清
时间复杂度 O ( n ) O(n) O(n)
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N=10000100;
int n,x,y,z,m[2];
int c[N],lenth[N],f[N],top;
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
int main(){freopen("brackets.in","r",stdin);freopen("brackets.out","w",stdout);n=read(),x=read(),y=read(),z=read(),m[0]=read(),m[1]=read(),c[0]=read(),c[1]=read();for(int i=2;i<n;i++) c[i]=(1ll*c[i-1]*x+1ll*c[i-2]*y+z)%m[i&1]+1;ull ans=0,tmp=0;for(int i=0;i<n;i++){if(~i&1) top++,lenth[top]=c[i],f[top]=tmp;else{tmp=0;while(top&&lenth[top]<=c[i]){c[i]-=lenth[top];ans+=lenth[top]+f[top];if(!c[i]) tmp=f[top]+1;top--;}if(top&&c[i]) lenth[top]-=c[i],ans+=c[i],tmp=1;}}printf("%llu\n",ans);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}B
用好 a i a_i ai 互不相同的性质,发现只需要记录 f i , S f_{i,S} fi,S 表示到 i i i,前一个与 a i a_i ai 的异或值为 S S S 的方案数
然后转移用前缀和优化可以到 O ( n 2 m ) O(n2^m) O(n2m)
但这样会考虑不到 i i i 前一个不合法的情况,因为集合不相交,所以直接减掉即可
时间复杂度 O ( n 2 m ) O(n2^m) O(n2m)
#include <bits/stdc++.h>
using namespace std;
const int N=4100,MAXS=4100;
const int P=998244353;
int n,m,s,a[N],rev[MAXS],f[N][MAXS],g[N],tot[N],sum[N][MAXS];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
inline void inc(int &x,int y){ x+=y;if(x>=P) x-=P;}
int main(){freopen("school.in","r",stdin);freopen("school.out","w",stdout);n=read(),m=read(),s=read();for(int i=1;i<=n;i++) a[i]=read(),rev[a[i]]=i;for(int i=1;i<=n;i++){tot[i]=tot[i-1];for(int S=0;S<1<<m;S++) sum[i][S]=sum[i-1][S];for(int S=0;S<1<<m;S++){int j=rev[S^a[i]];if(!j||j>=i) continue;f[i][S]=((1ll*tot[j-1]-sum[j-1][s^S]-g[j])%P+P)%P;inc(g[i],sum[j-1][s^S]);inc(tot[i],f[i][S]+j),inc(sum[i][S],f[i][S]+j);}}int ans=(n+n*(n-1)/2+1ll*n*(n-1)*(n-2)/6%P)%P;for(int i=1;i<=n;i++) for(int S=0;S<1<<m;S++) inc(ans,f[i][S]);printf("%d\n",ans);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}C
线段树优化建图的做法是显然的
考虑正解
我们假设我们有一张图,每个点都是指向 1 1 1 个区间(多个也没事),且边权为 1 1 1,我们是否可以不建出图, O ( n ) O(n) O(n) 求最短路
是可以的。我们只要用并查集维护这个点后面第一个未被访问到的点即可,然后在 b f s bfs bfs 的过程中便可以合并并查集,然后做到 O ( n ) O(n) O(n) 的复杂度(并查集不算)
但我们如何建出一个点指向区间的图呢
考虑做一个映射,我们令 j j j 为 i d % n id\%n id%n,把每个点归到类中去,那么类 j j j 可以到 [ j − R , j − L ] [j-R,j-L] [j−R,j−L] 的每一个类,这样就可以用上述方法 O ( n ) O(n) O(n) 计算了
感觉还是很妙的
#include <bits/stdc++.h>
using namespace std;
const int N=1000100,inf=1e9;
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
int dis[N<<1],ans[N];
int que[N],hh,tt;
int stk[N],hd,tl;
int fa[N];
int ne[N],h[N];
int get_father(int x){ return x==fa[x]?x:fa[x]=get_father(fa[x]);}
void insert(int l,int r,int Dist){for(int i=get_father(l);i<=r;i=get_father(i)){for(int u=h[i];~u;u=ne[u]) if(dis[u]==inf) dis[u]=Dist,que[++tt]=u;fa[i]=get_father(i+1);}
}
void work(){int n=read(),d=read(),L=read(),R=read(),q=read();for(int i=0;i<n;i++) h[i]=-1;for(int i=0;i<n;i++){int pos=1ll*i*d%n;ne[i]=h[pos],h[pos]=i;}for(int i=0;i<=n;i++) fa[i]=i;int D=R-L;for(int i=0;i<n;i++) dis[i]=inf;hh=0,tt=-1;dis[0]=0,que[++tt]=0;while(hh<=tt){int u=que[hh++];int t=(u-R+n)%n;if(t+D<n) insert(t,t+D,dis[u]+1);else insert(t,n-1,dis[u]+1),insert(0,D-(n-t),dis[u]+1);}for(int i=0;i<n;i++) dis[i+n]=dis[i];for(int i=0;i<n;i++) ans[i]=inf;hd=0,tl=-1;for(int i=2*n-1;i>=0;i--){if(i+L<2*n){while(hd<=tl&&dis[i+L]<=dis[stk[tl]]) tl--;stk[++tl]=i+L;}while(hd<=tl&&stk[hd]>i+R) hd++;if(hd<=tl&&i<n) ans[i]=dis[stk[hd]];}while(q--){int x=read();if(ans[x]>n+5) puts("-1");else printf("%d\n",ans[x]);}
}
int main(){freopen("calculator.in","r",stdin);freopen("calculator.out","w",stdout);int T=read();while(T--) work(); fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}D
考虑到约数和函数具有积性,因为 ∏ a i = m \prod a_i=m ∏ai=m,所以 ∏ σ ( a i ) = σ ( m ) \prod\sigma(a_i)=\sigma(m) ∏σ(ai)=σ(m)
所以我们可以快速算出部分 1 1 1
对于部分 2 2 2,我们可以把它理解成多项式,然后把它拆开成若干个乘积
于是我们可以 d p dp dp 求解
令 f i , a , b , c f_{i,a,b,c} fi,a,b,c 表示到第 i i i 个质数,前面选了 a a a 个 f 0 f0 f0, b b b 个 f 1 f1 f1, c c c 个 f 2 f2 f2 的方案和
这个是好转移的,有以下三种情况
- 不选这个质数
- 新建一个 f 0 f0 f0 或 f 1 f1 f1 或 f 2 f2 f2
- 放在原先的 f 0 f0 f0 或 f 1 f1 f1 或 f 2 f2 f2 中
这都是可以快速转移的
最后求答案的时候只要把为 1 1 1 的贡献计算进去即可
时间复杂度 O ( k 4 ) O(k^4) O(k4)
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int K=110,P=998244353;
int p[K],f[2][K][K][K];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
inline void inc(int &x,int y){ x=(x+y)%P;}
int qmi(int a,int b){a%=P;int res=1;for(;b;b>>=1){if(b&1) res=res*a%P;a=a*a%P;}return res;
}
signed main(){freopen("product.in","r",stdin);freopen("product.out","w",stdout);int na=read(),nb=read(),f0=read(),f1=read(),f2=read();int k=read();for(int i=1;i<=k;i++) p[i]=read();f[0][0][0][0]=1;for(int i=0;i<k;i++){memset(f[~i&1],0,sizeof(f[~i&1]));int t=min(nb,i);for(int a=0;a<=t;a++) for(int b=0;b<=t-a;b++) for(int c=0;c<=t-a-b;c++){int coef=na%P*(p[i+1]+1)%P,rs=(nb-a-b-c)%P*f[i&1][a][b][c]%P*coef%P;inc(f[~i&1][a][b][c],f[i&1][a][b][c]);//不放入任何的集合inc(f[~i&1][a+1][b][c],rs*f0);//放入ainc(f[~i&1][a][b+1][c],rs*f1%P*p[i+1]);//放入binc(f[~i&1][a][b][c+1],rs*f2%P*p[i+1]%P*p[i+1]);//放入cinc(f[~i&1][a][b][c],(a+1ll*b*p[i+1]+1ll*c*p[i+1]%P*p[i+1])%P*coef%P*f[i&1][a][b][c]);//放入之前的集合} }int t=min(nb,k);int ans=0;for(int a=0;a<=t;a++) for(int b=0;b<=t-a;b++) for(int c=0;c<=t-a-b;c++)inc(ans,f[k&1][a][b][c]*qmi(f0+f1+f2,(nb-a-b-c)%(P-1))); printf("%d\n",ans);fprintf(stderr,"%d ms\n",int64_t(1e3*clock()/CLOCKS_PER_SEC));return 0;
}
/*
f[i][a][b][c]:在前i个质数中,有a个选了f0,b个选了f1,c个选了f2的权值和
*/相关文章:

20231023 比赛总结
比赛链接 反思 A 花了很长时间,幸亏没怎么调就对了,以后还是应该先看其他题的 括号匹配题的套路感觉没有掌握透,感觉无非就是单调栈,哈希,折线图 B 感觉比 T 1 T1 T1 简单 C 正解还是很妙的,但 68…...

Vite创建vue3+ts+pinia+vant项目起步流程
pnpm介绍&安装 本质上他是一个包管理工具,和npm/yarn没有区别,主要优势在于 包安装速度极快磁盘空间利用效率高 安装: npm i pnpm -g使用: npm命令pnpm等效npm installpnpm installnpm i axiospnpm add axiosnpm i webpa…...

JVM 类的加载子系统
文章目录 类的加载过程加载阶段链接阶段初始化 类的加载器测试代码中获取对应的加载器获取加载器加载的路径不同类对应的加载器自定义加载器自定义加载器的方式 获取类的加载器的方式双亲委派机制双亲委派机制的好处 Java 的 SPI 机制1. 接口定义2. 具体实现3. 配置 META-INF/s…...

什么是1024程序员节
一年一度专属于程序员的节日“1024程序员节”要到来了,相信有很多的小伙伴跟我一样,对这个节日非常的熟悉,但也有一下小伙伴对这个节日非常陌生,没事,下面由我来讲解一下1024程序员节。 目录 节日背景 节日由来 社…...

spark获取hadoop服务token
spark 作业一直卡在accepted 问题现象问题排查1.查看yarn app日志2.问题分析与原因 问题现象 通过yarn-cluster模式提交spark作业,客户端日志一直卡在submit app,没有运行 问题排查 1.查看yarn app日志 appid已生成,通过yarn查看app状态为…...
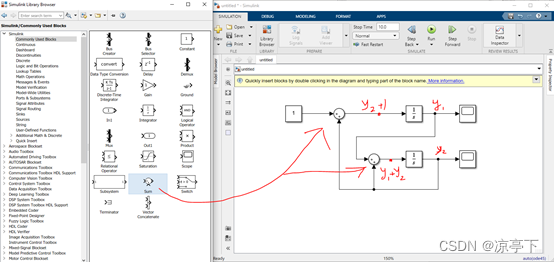
Simulink 最基础教程(一)
1.1基本概念 一个典型的Simulink模型大致如上图这样: 1)模块 block:图中画圈的那些,每个模块可以完成一些特定的任务,类似MATLAB中函数的概念。软件提供了很多模块,当然也可以自定义新的模块 2࿰…...

微信小程序:单行输入和多行输入组件
微信小程序提供了两种输入类型的输入框组件,分别是单行输入框 <input> 和多行输入框 <textarea>。 1. 单行输入组件(input) 单行输入框 <input> <input> 是一个用于收集用户输入的组件,主要用于收集单行…...

1024程序员
听说今天可以拿勋章,嘿嘿...

【Segment Anything Model】八:修改SAM源码做分类任务
🍉 博主微信 cvxiayixiao 🍓 【Segment Anything Model】计算机视觉检测分割任务专栏。 链接 🍑 【公开数据集预处理】特别是医疗公开数据集的接受和预处理,提供代码讲解。链接 🍈 【opencv+图像处理】opencv代码库讲解,结合图像处理知识,不仅仅是调库。链接 文章目…...
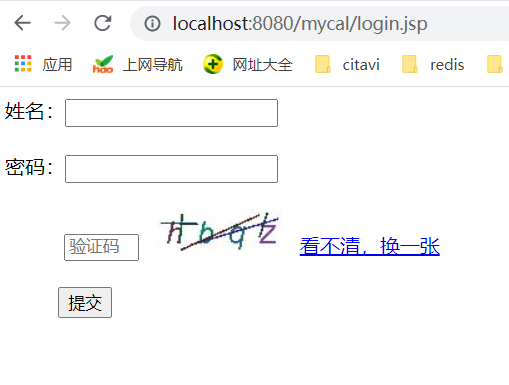
Java后端开发——实现登录验证程序
一、实现一个简单登录验证程序 实现一个简单的用户登录验证程序,如果用户名是 abc ,密码是 123,则显示欢迎用户的信息,否则显示“用户名或密码不正确”。 【分析】 该案例采用 JSP 页面只完成提交信息和验证结果的显示ÿ…...

CSS高频面试题
1.行内元素有哪些?块级元素有哪些?空元素有哪些?CSS的盒模型? 块级元素:div, p, h1-h6,form, ul ,li行内元素:a, b, br, span, i, input, select行内块级元素:img , input空元素:即没有内容的HTML元素,…...
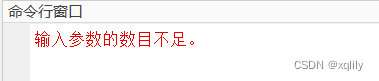
解决matlab报错“输入参数的数目不足”
报错语句:tanh((peakNums-parameter)/2) 报错提示:输入参数的数目不足 运行环境:matlab2021b 分析原因: 当执行peakNums - parameter时,如果peakNums和parameter都是向量,那么这并不一定意味着会得到对应…...

使用python_opencv比较图像差异/使用python_opencv找出两张图像的差异范围
目录 1 创建conda环境 2 安装python库 2.1 报错 ModuleNotFoundError: No module named numpy 3 image_diff.py...

NOIP2023模拟1联测22 爆炸
NOIP2023模拟1联测22 爆炸 题目大意 自己看 思路 当一个炸弹被引爆后,它的方向是固定的。如果被竖着引爆,那么应该选择横着引爆,否则选择竖着引爆,这是显然 的。 考虑对于每个炸弹 ( i , j ) (i , j) (i,j) 将第 i i i 行…...
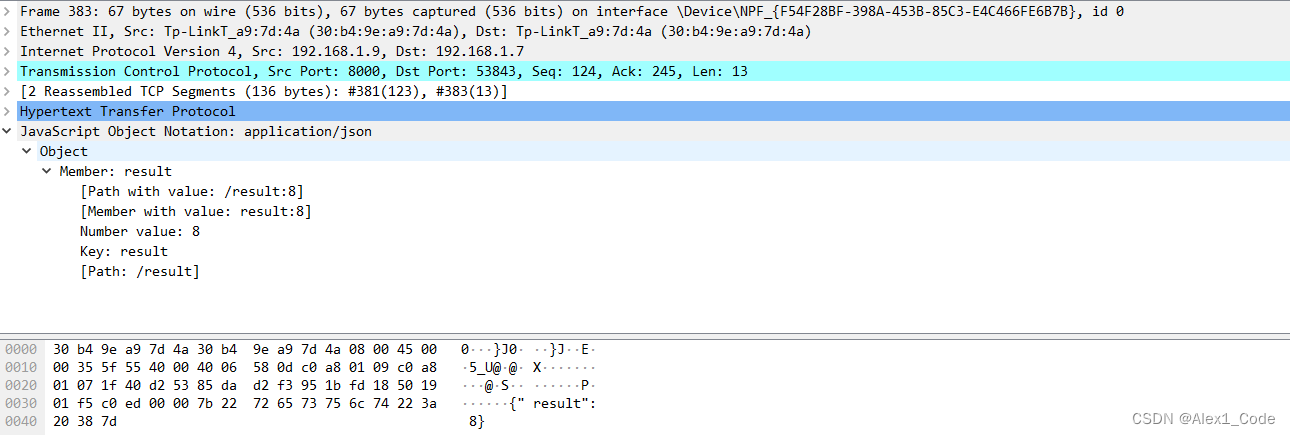
http post协议实现简单的rpc协议,WireShark抓包分析
文章目录 1.http 客户端-RPC客户端1.http 服务端-RPC服务端3.WireShark抓包分析3.1客户端到服务端的HTTP/JSON报文3.2服务端到客户端的HTTP/JSON报文 1.http 客户端-RPC客户端 import json import requests# 定义 RPC 客户端类 class RPCClient:def __init__(self, server_url…...

1024程序员节
一年一年真快啊,...

嵌入式--->怎样选择编译语言,C C++或是Rust?
C 老牌语言,不可替代,速度和资源占用都是嵌入式领域着重考虑的 Rust 作为新生语言,已经成长到可以和C进行竞争的地步,不论是速度还是资源占用看,还是安全性 C 嵌入式开发使用C的思想,可以极大地简化代码&am…...
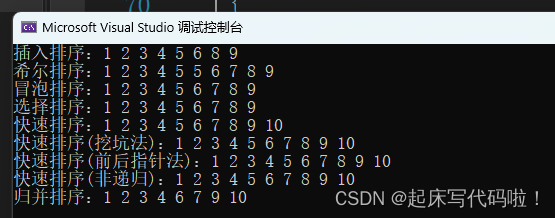
一起学数据结构(12)——归并排序的实现
1. 归并排序原理: 归并排序的大概原理如下图所示: 从图中可以看出,归并排序的整体思路就是把已给数组不断分成左右两个区间,当这个区间中的数据数量到达一定数值时,便返回去进行排序,整体的结构类似二叉树…...

读书笔记之《敏捷测试从零开始》(一)
大家好,我是rainbowzhou。 子曰:学而时习之,不亦说乎?今天我想和大家分享一本测试书籍——《敏捷测试从零开始》。以下为我的读书笔记: 精彩片段摘录: 焦虑往往来自于对比,当你在自己的圈子里面…...

视频亮度太低了,如何调高
充足、均匀、稳定的光亮对于视频制作是至关重要的,在现实生活中,不可预见的天气变化和拍摄地方的阴暗常常给我们留下暗淡无光的视频片段。 如果你的视频太暗想知道如何使它变亮,且又不知道使用哪个工具,那你无需担心,因…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
