IEEE754 标准存储浮点数

1. IEEE754 标准简介

IEEE754 标准是一种用于浮点数表示和运算的标准，由国际电工委员会（IEEE）制定。它定义了浮点数的编码格式、舍入规则以及基本的算术运算规则，旨在提供一种可移植性和一致性的方式来表示和处理浮点数
IEEE754 标准定义了两种常见的浮点数格式：单精度（32位）和双精度（64位）。这些格式使用了符号、阶码（指数）、尾数的二进制表示形式，其中符号表示浮点数的正负，指数表示浮点数的数量级，而尾数表示浮点数的精度。同时，IEEE754 标准还定义了特殊值，如正无穷大、负无穷大和 NaN（非数值）
IEEE754 标准还规定了浮点数的四种基本算术运算：加法、减法、乘法和除法。这些运算遵循一定的舍入规则，以确保结果在浮点数表示范围内具有最佳的精度和准确性
使用 IEEE754 标准可以提供一种统一的浮点数表示和运算方式，使得不同的计算机和编程语言之间可以进行浮点数数据的可靠交换和计算。需要注意的是，IEEE754 标准仍然存在一些舍入误差和精度限制，因此在进行浮点数运算时需要小心处理，并考虑数值精度可能导致的误差问题

2. float 的存储方式

float 占用 32 位的存储空间，32 位被分为了如下的三个部分，各个部分所占的位数如下图所示，右边为低位

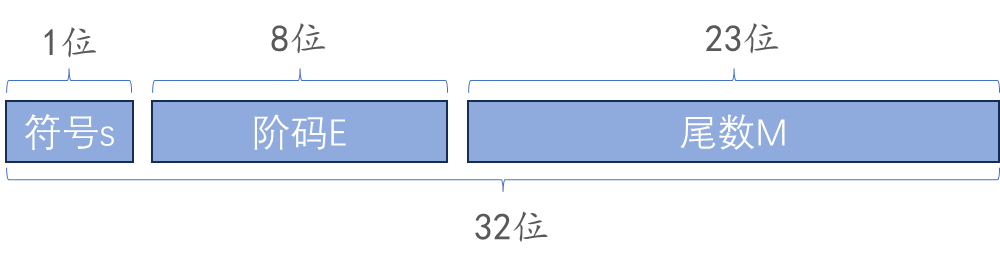
• 符号位：符号位为 0 说明该浮点数为正数，若为 1 则说明浮点数为负数
• 阶码：代表该浮点数被二进制科学表示法规范化后的指数，阶码采用移码表示，后面会有具体的例子进行讲解
• 尾数：被二进制规格化后要求小数点前一位数必须为 1，由于所有的浮点数都采用这样的方式进行处理，所以尾数中实际隐含了最高位 1，例如尾数为 M，则实际在还原时，相当于是 1.M，后面会有具体的例子进行讲解

设一个浮点数的符号存储的二进制为 s，阶码为 E，尾数为 M
则存储的该浮点数为：(-1)^s×1.M×2^E-偏置值，在单精度浮点数中，该偏置值为127
还需要注意的是，在 IEEE754 中，阶码全 0 和全 1 的情况被列为了特殊情况（后面的小节会讲到），所以阶码实际可以使用的范围为 1~254

2.1 浮点数如何转为 IEEE754 标准

例如现在有十进制数：85.125
其中整数部分为：85，对应二进制为 101 0101
小数部分为：0.125，对应二进制为 001
所以 85.125 对应的二进制就为：101 0101.001
规范化后：1.010101001 x 2^6
符号位为：0
阶码：6+127（偏置值）= 133
对应二进制为：133 = 10000101
尾码：010101001（注意这里的尾码实际上没有包含最高位的 1），由于这里没有 23 位，后续会补 0 直到尾码有 23 位
IEEE754 标准下的存储二进制为：

符号（1位）	阶码（8位）	尾数（23位）
0	1000 0101	010 1010 0100 0000 0000 0000

对应的十六进制数为：42 AA 40 00

2.2 IEEE754 标准如何转化为浮点数

现有符合 IEEE754 标准的以十六进制存储的浮点数：C1 51 00 00
转为二进制数然后将每一位与之含义对应：

符号（1位）	阶码（8位）	尾数（23位）
1	1000 0010	101 0001 0000 0000 0000 0000

其中：
s = 1
M = 101 0001 0000 0000 0000 0000 对应十进制为：.6328125（需要注意的是，这里的数值代表的是小数点后面的数值）
E = 1000 0010 对应的十进制为 130
然后我们带入上面给出的公式中 (-1)¹×1.6328125×2^130-127 = -1.6328125×2³ = -1.6328125×8 = -13.0625
所以 C1 51 00 00 所代表的浮点数就是 -13.0625

3. double 的存储方式

double 占用 64 位的存储空间，64 位被分为了如下的三个部分，各个部分所占的位数如下图所示，右边为低位

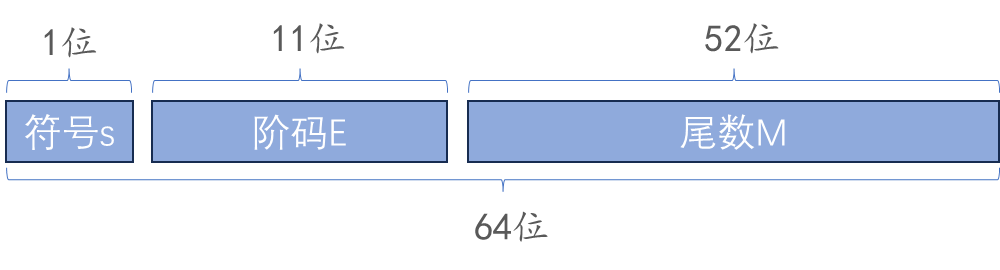
双精度浮点数中，该偏置值为1023，阶码实际可以使用的范围为 1~2046。其余的存储方式与 float 是一样的，这里就不再赘述

4. IEEE754 制定的特殊值

当阶码全为 0：

• 尾数 M 不全为 0 时，表示非规格化小数：±(0.xxx…xx)×2^-126
• 尾数 M 全为 0 时，表示真值 ±0

当阶码全为 1：

• 尾数 M 全为 0：表示无穷大
• 尾数 M 不全为 0：表示数值“NAN”，如0/0、∞-∞等

4.1 浮点数的存储范围

有了前面小节的铺垫，相信很容易可以求出来 float 的存储范围了，首先来寻找 float 可以表示的最大值（无穷除外）：
让符号为 0，阶码为 254，尾数全部为 1，这样我们可以得到下面的二进制

符号（1位）	阶码（8位）	尾数（23位）
0	1111 1110	111 1111 1111 1111 1111 1111

带入公式：(-1)⁰×(2-2^-23)×2^254-127 =(2-2^-23)×2¹²⁷ = 2¹²⁸-2¹⁰⁴
这个就是 float 可以表示的最大的值，只要加上负号就是它可以表示的最小的值
但这还不是我们的目标，根据上面的学习我们知道了 float 在靠近 0 的地方其实会有很多的数字不能表示到，那么他可以表示的最小/大的规范化正/负数是多少呢？
我们来考虑在什么情况下，float 可以取到最小规范化正数的值：
让符号为 0，阶码为 1，尾数全部为 0，这样我们可以得到下面的二进制

符号（1位）	阶码（8位）	尾数（23位）
0	0000 0001	000 0000 0000 0000 0000 0000

带入公式：(-1)⁰×1.0×2^1-127 =2^-126
这个就是 float 可以表示的最小规范化正数的值，只要加上负号就是它可以表示的最大规范化负数的值
double类型可以根据上面的方法如法炮制，这里就不再赘述，具体的范围可以参考下面的表格

格式	最小正值	最大正值
float	2-126	(2-2-23)×2127
double	2-1022	(2-2-52)×21023

格式	最大负值	最小负值
float	(2-23-2)×2127	-2-126
double	(2-52-2)×21023	-2-1022

根据上面的表格可以看到浮点数并不是连续的表示数轴上的数（准确的说浮点数本身就只能间断的表示某一些数，但是我这里所说间断指的是在一大段的范围内，浮点数都是无法表示的，比如 float 类型从 0~2^-126 这一段的数字它就无法进行表示），可以参考下面的图示

当发生下溢时，会被当做机器零处理，发生上溢时，会被当做无穷来处理
IEEE754 还制定了浮点数运算的规则，有兴趣的读者可以自行查阅，本文就不做说明了