【T】03
A 【模板】快速幂
板子,略
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll a,p,k;
int main()
{scanf("%lld%lld%lld",&a,&p,&k);printf("%lld^%lld mod %lld=",a,p,k);ll ans=1,w=a;a%=k;while(p){if(p&1){ans=ans*w%k;}w=w*w%k;p>>=1;}printf("%lld",ans%k);
}B【模板】矩阵快速幂
#include<bits/stdc++.h>
using namespace std;
long long mod=1000000007;
long long n,k;
struct sq{long long num[102][102];sq(){memset(num,0,sizeof(num));}//初始化num数组为空
};
sq operator *(const sq &a,const sq &b)
{sq ans;for(int k=1;k<=n;k++)for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){ans.num[i][j]=(ans.num[i][j]+a.num[i][k]*b.num[k][j]%mod)%mod;}}return ans;
}//一个重载
sq x,y,ans;
long long read()
{char s;long long ans=0;s=getchar();while(s>'9'||s<'0'){s=getchar();}while(s>='0'&&s<='9'){ans=ans*10+s-'0';s=getchar();}return ans;
}//只是个快速读入函数
inline void init()
{n=read();k=read();//用scanf,cin也行for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)x.num[i][j]=read();for(int i=1;i<=n;i++){y.num[i][i]=1;ans.num[i][i]=1;}
}
int main(){init();while(k){if(k&1){ans=ans*x;}x=x*x;k>>=1;}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%lld ",ans.num[i][j]);printf("\n");}return 0;
}
C【模板】有理数取余
除以一个数等于乘以它的逆元,逆元可以用费马小定理求
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll a,b,mod=19260817;
inline ll read()
{ll ans=0;char s=getchar();while(s>'9'||s<'0')s=getchar();while(s>='0'&&s<='9'){ans=((ans<<1)%mod+(ans<<3)%mod+(s&15))%mod;s=getchar();}return ans;
}
ll quick_m(ll i,ll n)
{i%=mod;ll ans=1,ds=i;while(n){if(n&1){ans=ans*ds%mod;}ds=ds*ds%mod;n>>=1;}return ans%mod;
}
signed main(){a=read();b=read();if(b==0){printf("Angry!");return 0;}printf("%lld",a*quick_m(b,mod-2)%mod);return 0;
}
D 质因数分解
#include<bits/stdc++.h>
int a;
int main()
{scanf("%d",&a);for(int i=2;i*i<=a;i++){if(a%i==0){printf("%d",std::max(a/i,i));return 0;//找到一个因数就可以停了,另一个因数就是最大的那个}}
}
E 质数筛
数据不大的话,每个数都直接用质数判断法也能过
#include<bits/stdc++.h>
using namespace std;
int n,a;
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a);bool f=1;for(int j=2;j*j<=a;j++){if(a%j==0){f=0;break;}}if(f==1&&a!=1)printf("%d ",a);//是质数}
}
F 【模板】线性筛素数
这里用的欧拉筛
#include<bits/stdc++.h>
using namespace std;
bool ans[100000002];
int z[6000005],p;
int n,m,a;
int main()
{scanf("%d%d",&n,&m);for(int i=2;i<=n;i++){if(!ans[i])z[++p]=i;//printf("[%d]",z[p]);for(int j=1;j<=p&&z[j]*i<=n;j++){ans[i*z[j]]=1;if(i%z[j]==0)break;}}for(int i=1;i<=m;i++){scanf("%d",&a);printf("%d\n",z[a]);}return 0;
}
G 晨跑
求三个数的最小公倍数
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll gcd(ll x,ll y){return !y?x:gcd(y,x%y);}
ll lcm(ll x,ll y){return x*y/gcd(x,y);}
int main()
{ll a,b,c;scanf("%lld%lld%lld",&a,&b,&c);printf("%lld",lcm(a,lcm(b,c)));
}
H 最大公约数和最小公倍数问题
x ∗ y = g c d ( x , y ) ∗ l c m ( x , y ) x*y=gcd(x,y)*lcm(x,y) x∗y=gcd(x,y)∗lcm(x,y)
枚举x然后判断算出对应y是否满足gcd,lcm就行,可能要特判
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll gcd(ll x,ll y){return !y?x:gcd(y,x%y);}
ll lcm(ll x,ll y){return x*y/gcd(x,y);}
int main()
{ll a,b,ans=0;scanf("%lld%lld",&a,&b);if(a==b)ans--;//这样会存在x,y相同的一组,下面枚举时会多算一组,故删去for(ll i=1;i*i<=a*b;i++)if(a*b%i==0&&gcd(i,a*b/i)==a)ans+=2;printf("%lld",ans);
}
I 【模板】模意义下的乘法逆元
建议看我之前博客线性递推式部分
a − 1 = − ⌊ p / a ⌋ ∗ ( p m o d a ) − 1 ( m o d p ) a^{-1}=-⌊p/a⌋*(p \ mod \ a )^{-1} \ \ \ \ (mod \ p) a−1=−⌊p/a⌋∗(p mod a)−1 (mod p)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,p,inv[3000005];
signed main(){scanf("%d%d",&n,&p);inv[0]=1;inv[1]=1;printf("1\n");for(int i=2;i<=n;i++){inv[i]=(ll)inv[p%i]*(p-p/i)%p;//-p/i不能直接取模,要+p变成正数再%pprintf("%d\n",inv[i]);}return 0;
}
/*下面是欧拉筛版
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=3000005;
ll n,p;
bool vis[N];
ll z[N];
ll inv[N];
ll quick(ll a,ll k,ll mod)
{ll ans=1,as=a;while(k){if(k&1){ans=ans*as%mod;}as=as*as%mod;k>>=1;}return ans;
}
int main()
{scanf("%lld%lld",&n,&p);vis[1]=1,inv[1]=1;for (int i=2;i<=n;i++){//printf("(%d\n",i);if (!vis[i])z[++z[0]]=i,inv[i]=quick(i,p-2,p);for (int j=1;j<=z[0]&&i*z[j]<=n;j++){vis[i*z[j]]=1;inv[i*z[j]]=(inv[i]*inv[z[j]])%p;if (i%z[j]==0) break;}}for (int i=1;i<=n;i++)printf("%lld\n",inv[i]);return 0;
}*/
J 沙拉公主的困惑
求 1 − > N ! 1->N! 1−>N!中与 M ! M! M!互质的个数
推演一下,最后得 N ! M ! ϕ ( M ! ) \frac {N!}{M!} \phi{(M!)} M!N!ϕ(M!)
=> N ! ( 1 − p 1 p 1 ) ( 1 − p 2 p 2 ) . . . ( 1 − p k p k ) N!(\frac {1-p_1}{p_1})(\frac {1-p_2}{p_2})...(\frac {1-p_k}{p_k}) N!(p11−p1)(p21−p2)...(pk1−pk)
一堆预处理,质数+线性求逆+阶乘。。。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline ll read()
{ll ans=0;char s=getchar();while(!isdigit(s))s=getchar();while(isdigit(s)){ans=(ans*10)+(s&15);s=getchar();}return ans;
}
const int N=1e7+10;
int T;
ll n,m,mod;
int z[N],p;
bool vis[N];
void get_prime()
{for(int i=2;i<N;i++){if(!vis[i])z[++p]=i;for(int j=1;j<=p&&i*z[j]<N;j++){vis[i*z[j]]=1;if(i%z[j]==0)break;}}
}
ll inv[N],mul[N],pt[N];
int main()
{scanf("%d%lld",&T,&mod);get_prime();inv[1]=1;inv[0]=1;for(int i=2;i<N;i++)inv[i]=inv[mod%i]*(mod-mod/i)%mod;mul[1]=1;for(int i=2;i<N;i++)mul[i]=mul[i-1]*i%mod;pt[1]=1;for(int i=2;i<N;i++)if(!vis[i])pt[i]=pt[i-1]*(i-1)%mod*inv[i%mod]%mod;else pt[i]=pt[i-1];while(T--){n=read();m=read();printf("%lld\n",mul[n]*pt[m]%mod);}
}//开个o2就过了
K 同余方程
扩欧板子题
#include<bits/stdc++.h>
using namespace std;
void gcd(int a,int b,int &x,int &y)
{if(!b){x=1;y=0;return ;}gcd(b,a%b,x,y);int xx=y,yy=x-a/b*y;x=xx;y=yy;return ;
}
int a,b,x,y;
int main()
{scanf("%d%d",&a,&b);gcd(a,b,x,y);printf("%d",(x+b)%b);
}
相关文章:

【T】03
A 【模板】快速幂 板子,略 #include<bits/stdc.h> #define ll long long using namespace std; ll a,p,k; int main() {scanf("%lld%lld%lld",&a,&p,&k);printf("%lld^%lld mod %lld",a,p,k);ll ans1,wa;a%k;while(p){if(p…...

VBA技术资料MF73:将Logo添加到页眉侧
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...
)
听GPT 讲Rust源代码--library/std(1)
std git:(master) ✗ tree.├── Cargo.toml├── benches│ ├── hash│ │ ├── map.rs│ │ ├── mod.rs│ │ └── set_ops.rs│ └── lib.rs├── build.rs├── src│ ├── alloc.rs│ ├── ascii.rs│ ├── backtrace│ │…...

Vue源码总结
1,根据vue工程package.json配置文件查看scripts命令,找到build命令执行的js文件 2,根据构建执行的js文件继续跟进,找到主入口文件 3,从主入口文件直接分析主干代码,追踪export的Vue对象 4,跟…...

记一次调试微信订阅消息的坑
微信发送订阅消息文档 发送订阅消息 | 微信开放文档 按照文档说明的,一直报data param错误,编码47001,从程序中把请求参数扣出来,放到微信提供的工具里面调试 微信调试工具 然后报data参数要用string,转化为string…...

ASP.NET Core3.1 API 创建(Swagger配置、数据库连接Sql Server)、开发、部署
文章目录 创建项目点击Nuget安装包删除原有controllers编辑新建controll、添加注释Startup 注册Swagger服务使用swagger中间件配置XML注释更改启动端口 launchsettings.json在startup.cs跨域处理运行 数据库设计与连接安装库新建类继承框架根据数据库表设计对应设计类在DataCon…...
)
大数据之LibrA数据库常见术语(八)
SCTP Stream Control Transmission Protocol,流控制传输协议。是IETF于2000年新定义的一个传输层协议。是提供基于不可靠传输业务的协议之上的可靠的数据报传输协议。SCTP的设计用于通过IP网传输SCN窄带信令消息。 Session 数据库系统在接收到应用程序的连接请求时…...
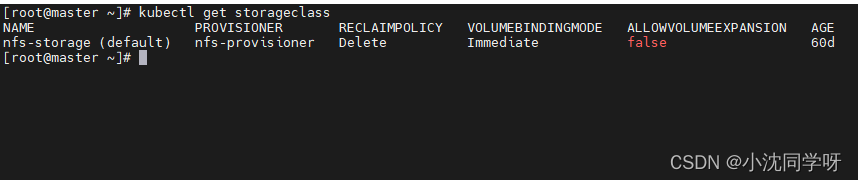
【实战】Kubernetes安装持久化工具NFS-StorageClass
文章目录 前言技术积累存储类(storage class)什么是NFS什么是PV\PVC为什么要用NFS-StorageClass 安装NFS-StorageClass保证K8S集群正常投用安装NFS工具与客户端NFS安装常见错误安装NFS-StorageClass存储器 前言 前面的博文我们介绍了如何用kuberadmin的…...

透明安全地解释Moonbeam基金会分配的GLMR去了哪
在GLMR分配比例中,约有16.7%的GLMR分配给了生态支持。这部分GLMR究竟用在了哪里,Moonbeam生态是否还有足够的GLMR扶持生态项目? Moonbeam基金会每隔半年会发布一份GLMR透明度报告,最近的报告日期为2023年7月31日。其中列出了社区…...

python安装包失败 安装scipy包
最近在配深度学习环境,安装好了conda、CUDA、cuDNN,运行之后报错,没有scipy包。 试了很多方法: 用命令行pip、conda install 在pycharm下载包 在环境中添加包 都失败了 要么直接ERROR,要么超时 问了师兄 需要在conda环…...
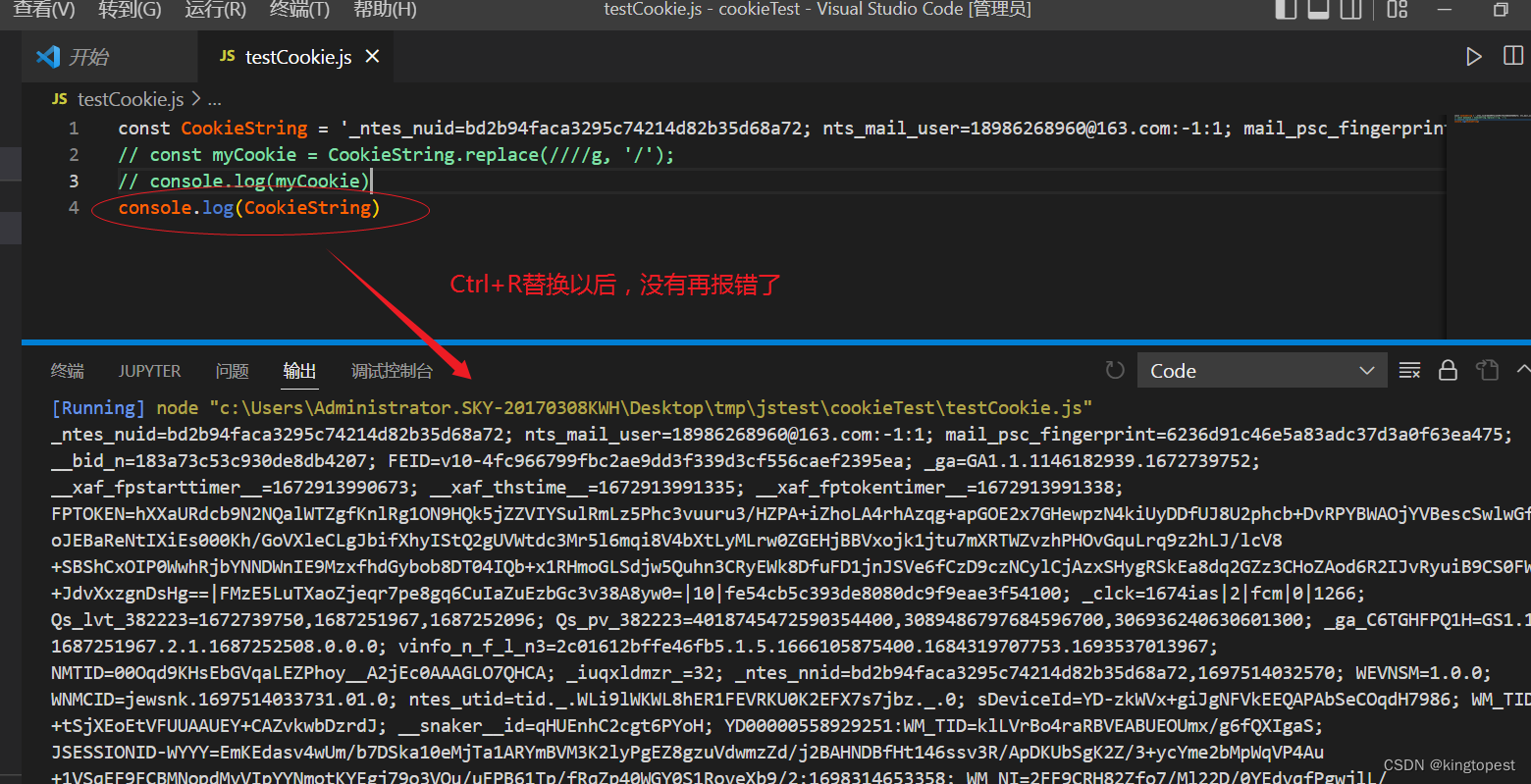
解决javascript报错:SyntaxError: Invalid Unicode escape sequence
在处理cookie时报这个错: 网上搜了一圈都说是反斜杠问题,要把\替换成/ 但是试了网上的replace替换: replace(/\\/g, /) 结果没有用!!! 然后我干脆直接做了一个最简单字符串赋值,再打印出来。…...

【Python第三方包】使用Python的Translate包进行文本翻译
文章目录 前言一、Translator类的初始化参数二、translate函数三、翻译示例代码1.1 示例代码11.2 示例代码2总结前言 在现代互联网时代,跨语言翻译已经成为了不可或缺的工具。不仅对于个人,对于企业和开发者来说,实现文本翻译在国际化、多语言支持以及内容本地化方面都具有…...
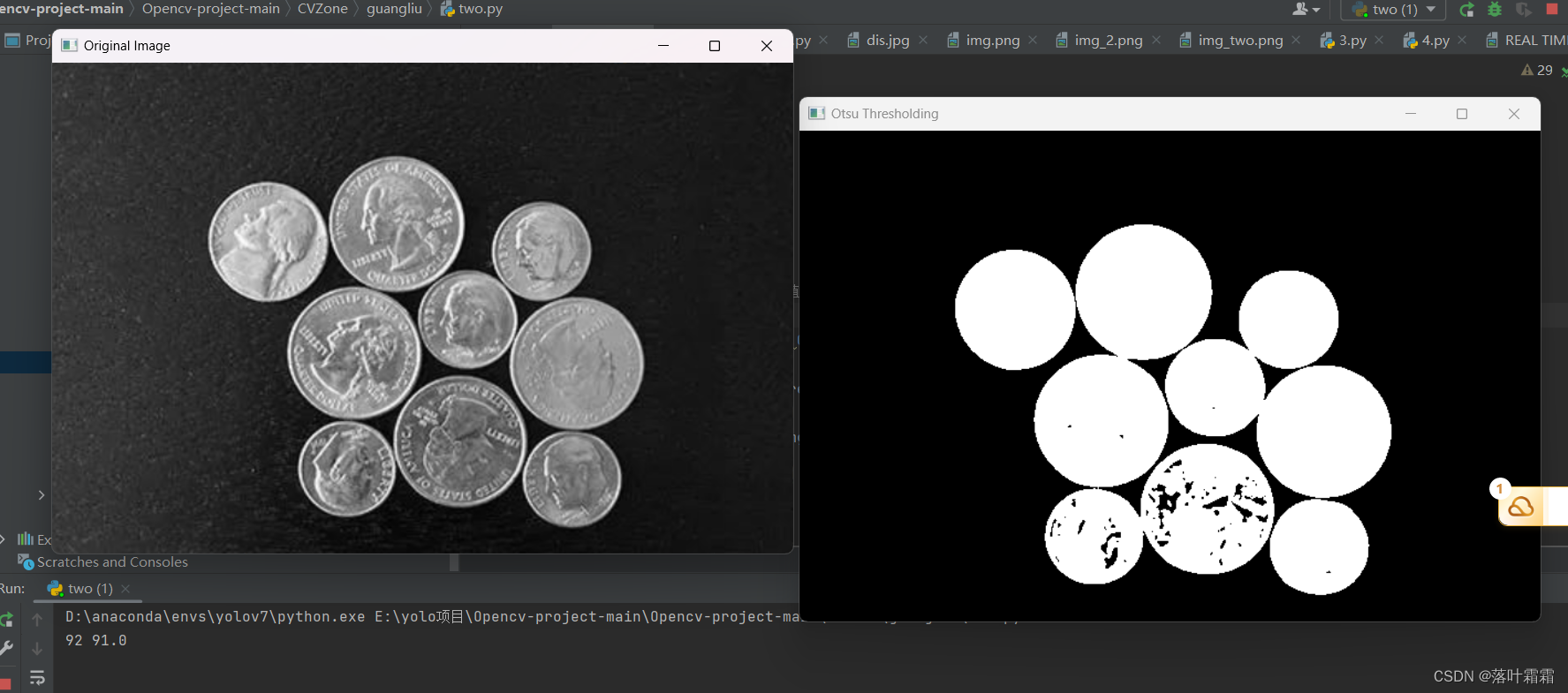
【OpenCV实现图像阈值处理】
文章目录 概要简单阈值调整自适应阈值调整大津(Otsus)阈值法Otsus 二值化是如何工作的 概要 OpenCV库中的图像处理技术,主要分为几何变换、图像阈值调整和平滑处理三个部分。 在几何变换方面,OpenCV提供了cv.warpAffine和cv.warpPerspective函数&#…...

【Python机器学习】零基础掌握StackingRegressor集成学习
如何更准确地预测糖尿病患者的血糖水平? 糖尿病是一种影响全球数百万人的慢性疾病。有效地管理和预测血糖水平是糖尿病患者日常生活的重要一环。单一的预测模型(比如线性回归、支持向量机等)虽然有一定的效果,但在处理复杂的医疗数据时,其准确性可能会受到限制。 为了准…...

JVM(Java Virtual Machine)G1收集器篇
前言 本文参考《深入理解Java虚拟机》,本文主要介绍G1收集器的收集思想和具体过程(填上一篇文章留下的坑) 本系列其他文章链接: JVM(Java Virtual Machine)内存模型篇 JVM(Java Virtual Machi…...
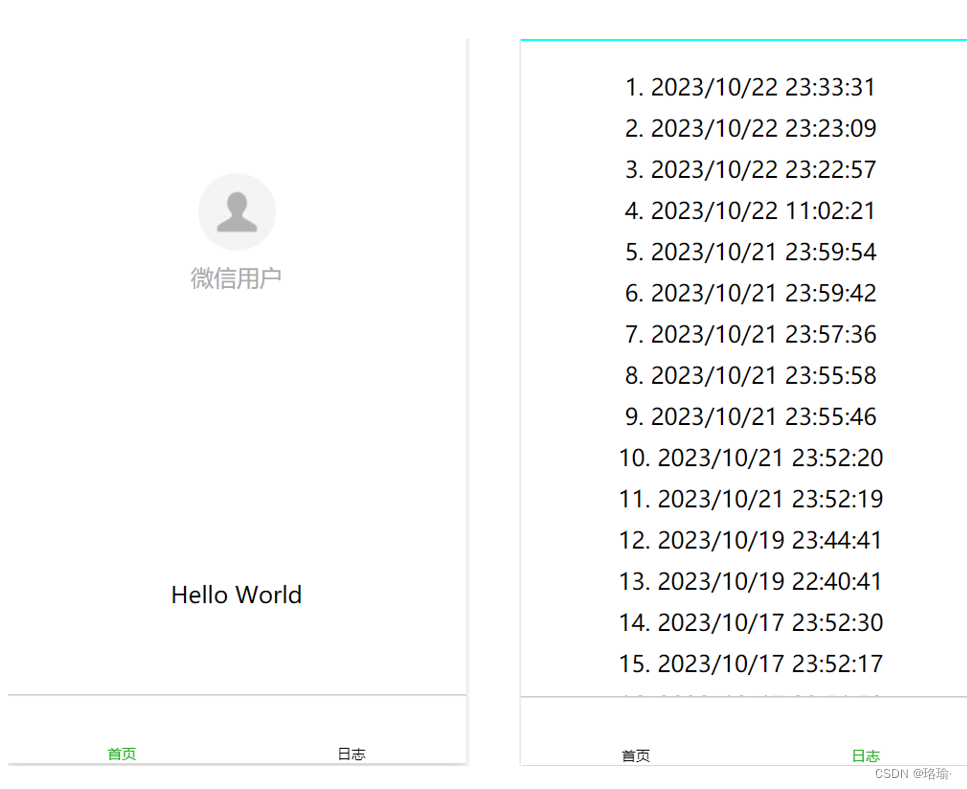
微信小程序设计之主体文件app-json-tabBar
一、新建一个项目 首先,下载微信小程序开发工具,具体下载方式可以参考文章《微信小程序开发者工具下载》。 然后,注册小程序账号,具体注册方法,可以参考文章《微信小程序个人账号申请和配置详细教程》。 在得到了测…...

GZ035 5G组网与运维赛题第2套
2023年全国职业院校技能大赛 GZ035 5G组网与运维赛项(高职组) 赛题第2套 一、竞赛须知 1.竞赛内容分布 竞赛模块1--5G公共网络规划部署与开通(35分) 子任务1:5G公共网络部署与调试(15分) 子任务2:5G室内与室外站点建设(20分) 竞赛模块2--5G公共网络运维与优化(…...

如何训练Embedding Model
BGE的技术亮点: 高效预训练和大规模文本微调;在两个大规模语料集上采用了RetroMAE预训练算法,进一步增强了模型的语义表征能力;通过负采样和难负样例挖掘,增强了语义向量的判别力;借鉴Instruction Tuning的…...

springboot配置redis、Spring cache
1.Jedis库 依赖库 <dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId><version>5.0.2</version> </dependency>使用案例: Testpublic void jedis(){Jedis jedis new Jedis("127…...

悟空crm安装搭建 报错[0] RedisException in Redis.php line 56问题处理办法
相信很多朋友进行安装悟空crm的时候 提示错误: [0] RedisException in Redis.php line 56 Connection refused 不知道怎么样处理是吧~~~ $this->options array_merge($this->options, $options);}# redis 密码$password config(cache.password);if (!empty…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...
