【机器学习】KNN算法-模型选择与调优
KNN算法-模型选择与调优
文章目录
- KNN算法-模型选择与调优
- 1. 交叉验证
- 2. 超参数搜索-网格搜索(Grid Search)
- 3. 模型选择与调优API
- 4. 鸢尾花种类预测-代码和输出结果
- 5. 计算距离
问题背景:KNN算法的K值不好确定
1. 交叉验证
交叉验证:将拿到的训练数据,分为训练集和验证集。以下表为例:将数据分成4份,其中一份作为验证集,然后经过4次(组)的测试,每次都更换不同的验证集。即得到4组模型的结果,取平均值作为最终的结果。这种又称作为4折交叉认证。
| 第一块 | 第二块 | 第三块 | 第四块 | 准确率 |
|---|---|---|---|---|
| 验证集 | 训练集 | 训练集 | 训练集 | 80% |
| 训练集 | 验证集 | 训练集 | 训练集 | 78% |
| 训练集 | 训练集 | 验证集 | 训练集 | 75% |
| 训练集 | 训练集 | 训练集 | 验证集 | 82% |
我们之前知道数据分为训练集和测试集,但是为了从训练得到的模型结果更加准确,做出以下处理
- 训练集=训练集+验证集
- 测试集=测试集
2. 超参数搜索-网格搜索(Grid Search)
通常情况下,有很多参数是要手动去指定的,如KNN算法中的K值,这种叫超参数。但是手动过程繁杂,我们可能会定义一个列表,里面有一堆K的值来遍历选择,相当于“暴力破解”。而网格搜索会采用交叉认证来进行评估,在你给定的一定范围内的K值中选出最优参数组合建立模型。
3. 模型选择与调优API
- sklearn.model_selection.GridSearchCV(estimator,param_grid=None,cv=None)
- 对估计器的指定参数值进行详尽搜索
- estimator估计器对象
- param_grid:估计器参数(dict){“n_neighbors":[1,3,5]}
- cv:指定几折交叉验证
- fit():输入训练数据
- score():准确率
- 结果分析:best_params_最佳参数,best_score_最佳结果,best_estimator_最佳估计器,cv_results_交叉验证结果
4. 鸢尾花种类预测-代码和输出结果
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV# K—近邻算法
def KNN_demo():"""sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')n_neighbors:int可选,默认为5,k_neighbors查询默认使用的邻居数algorithm:{'auto','ball_tree','kd_tree','brute'},可选用于计算最近邻居的算法:‘ball_tree’将会使用BallTree,'kd_tree'将会使用KDTree。'auto'将尝试根据传递给fit方法的值来决定最合适的算法。(不同实现方式影响效率):return:"""# 获取数据iris = load_iris()# 划分数据集x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state= 6)# 特征工程 标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# KNN算法预估器estimator = KNeighborsClassifier(n_neighbors= 3)estimator.fit(x_train, y_train)# 模型评估# 方法一:y_predict = estimator.predict(x_test)print("y_predict:\n", y_predict)print("直接比对真实值和预测值:\n", y_test == y_predict)# 方法二:score = estimator.score(x_test, y_test)print("准确率为:\n", score)return None# KNN添加网格搜索和交叉认证
def KNN_gscv_demo():# 获取数据iris = load_iris()# 划分数据集x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)# 特征工程 标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# KNN算法预估器estimator = KNeighborsClassifier()# 加入网格搜索和交叉认证param_dict = {"n_neighbors": [1, 3, 5, 7, 9, 11]}estimator = GridSearchCV(estimator, param_grid= param_dict, cv =10)estimator.fit(x_train, y_train)# 模型评估# 方法一:y_predict = estimator.predict(x_test)print("y_predict:\n", y_predict)print("直接比对真实值和预测值:\n", y_test == y_predict)# 方法二:score = estimator.score(x_test, y_test)print("准确率为:\n", score)# 最佳print("最佳参数为:\n", estimator.best_params_)print("最佳结果:\n", estimator.best_score_)print("最佳估计器:\n", estimator.best_estimator_)print("交叉验证结果:\n", estimator.cv_results_)# 交叉验证结果为:训练集划分训练集和验证集之后的,不是整体的,和测试集无关return Noneif __name__ == "__main__":# KNN_demo() 没有添加网格搜索和交叉认证KNN_gscv_demo()pass
y_predict:[0 2 0 0 2 1 2 0 2 1 2 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 12]
直接比对真实值和预测值:[ True True True True True True True True True True True TrueTrue True True False True True True True True True True TrueTrue True True True True True True True True True False TrueTrue True]
准确率为:0.9473684210526315
最佳参数为:{'n_neighbors': 11}
最佳结果:0.9734848484848484
最佳估计器:KNeighborsClassifier(n_neighbors=11)
交叉验证结果:{'mean_fit_time': array([0.00010171, 0. , 0.00030091, 0. , 0. ,0.00020049]), 'std_fit_time': array([0.00030513, 0. , 0.00045964, 0. , 0. ,0.00040097]), 'mean_score_time': array([0.00110393, 0.00069332, 0.00051594, 0.00090301, 0.00085185,0.0005013 ]), 'std_score_time': array([0.00070476, 0.00039479, 0.00065858, 0.00030101, 0.00032043,0.0005013 ]), 'param_n_neighbors': masked_array(data=[1, 3, 5, 7, 9, 11],mask=[False, False, False, False, False, False],fill_value='?',dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}, {'n_neighbors': 11}], 'split0_test_score': array([1., 1., 1., 1., 1., 1.]), 'split1_test_score': array([0.91666667, 0.91666667, 1. , 0.91666667, 0.91666667,0.91666667]), 'split2_test_score': array([1., 1., 1., 1., 1., 1.]), 'split3_test_score': array([1. , 1. , 1. , 1. , 0.90909091,1. ]), 'split4_test_score': array([1., 1., 1., 1., 1., 1.]), 'split5_test_score': array([0.90909091, 0.90909091, 1. , 1. , 1. ,1. ]), 'split6_test_score': array([1., 1., 1., 1., 1., 1.]), 'split7_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 1. ,1. ]), 'split8_test_score': array([1., 1., 1., 1., 1., 1.]), 'split9_test_score': array([0.90909091, 0.81818182, 0.81818182, 0.81818182, 0.81818182,0.81818182]), 'mean_test_score': array([0.96439394, 0.95530303, 0.97272727, 0.96439394, 0.96439394,0.97348485]), 'std_test_score': array([0.04365767, 0.0604591 , 0.05821022, 0.05965639, 0.05965639,0.05742104]), 'rank_test_score': array([5, 6, 2, 3, 3, 1])}5. 计算距离
K最近邻(KNN)是一种有监督的机器学习算法,它根据其K个最近邻居的大多数类别来对数据点进行分类。在使用KNN时,需要确定一个距离度量来衡量数据点之间的相似性。常用的KNN距离度量包括欧氏距离、曼哈顿距离和闵可夫斯基距离。
-
欧氏距离:
-
欧氏距离是KNN中最常用的距离度量。
-
它是欧几里得空间中两个点之间的直线距离
-
在二维空间中,计算两个点(x1,y1)和(x2,y2)之间的欧氏距离的公式如下:
( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 \sqrt{(x1 - x2)^2 + (y1 - y2)^2} (x1−x2)2+(y1−y2)2
-
在n维空间中,公式扩展为:
∑ i = 1 n ( x i − y i ) 2 \sqrt{\sum_{i=1}^{n}(x_i - y_i)^2} i=1∑n(xi−yi)2 -
这种距离度量对特征的尺度敏感,因此在使用时重要的是标准化或归一化特征。
-
-
曼哈顿距离:
-
它以每个维度上的坐标绝对差的总和来衡量两个点之间的距离。
-
在二维空间中,计算两个点(x1,y1)和(x2,y2)之间的曼哈顿距离的公式如下:
∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ |x1 - x2| + |y1 - y2| ∣x1−x2∣+∣y1−y2∣ -
在n维空间中,公式扩展为:
∑ i = 1 n ∣ x i − y i ∣ \sum_{i=1}^{n}|x_i - y_i| i=1∑n∣xi−yi∣ -
曼哈顿距离对异常值不太敏感,因此在数据可能不服从正态分布的情况下,它是更好的选择。
-
-
闵可夫斯基距离:
- 闵可夫斯基距离是欧氏距离和曼哈顿距离的通用化。
- 它包括一个参数“p”,可以调整以将公式转换为欧氏或曼哈顿距离。
- 当p=2时,它变为欧氏距离,当p=1时,它变为曼哈顿距离。
- 两点(x,y)之间的闵可夫斯基距离的公式如下:
( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 / p \left(\sum_{i=1}^{n}|x_i - y_i|^p\right)^{1/p} (i=1∑n∣xi−yi∣p)1/p
默认情况下,KNN使用欧氏距离作为距离度量。如果使用不同的距离度量(例如曼哈顿或闵可夫斯基距离),可以在KNeighborsClassifier构造函数中使用“metric”参数进行指定。例如:
estimator = KNeighborsClassifier(metric='manhattan')
相关文章:

【机器学习】KNN算法-模型选择与调优
KNN算法-模型选择与调优 文章目录 KNN算法-模型选择与调优1. 交叉验证2. 超参数搜索-网格搜索(Grid Search)3. 模型选择与调优API4. 鸢尾花种类预测-代码和输出结果5. 计算距离 问题背景:KNN算法的K值不好确定 1. 交叉验证 交叉验证&#x…...

NPM【问题 01】npm i node-sass@4.14.1报错not found: python2及Cannot download问题处理
node-sass安装问题处理 1.问题2.处理2.1 方案一【我的环境失败】2.2 方案二【成功】2.3 方案三【成功】 1.问题 gyp verb which failed Error: not found: python2 # 1.添加Python27的安装路径到环境变量 gyp verb check python checking for Python executable "python…...

redis集群中节点fail,noaddr
文章目录 1. 问题:fail,noaddr2. cluster nodes节点信息解读2.1 每个字段的含义2.2 flags字段各标记含义 3. redis集群fail,noaddr问题解决4. cluster指令5. 相关文章(1) redis集群搭建(2) 华为云两台机器内网互联(3) /etc/rc.d/init.d 详解|程序开机自启(4) Redis5…...
Fourier分析导论——第1章——Fourier分析的起源(E.M. Stein R. Shakarchi)
第 1 章 Fourier分析的起源 (The Genesis of Fourier Analysis) Regarding the researches of dAlembert and Euler could one not add that if they knew this expansion, they made but a very imperfect use of it. They were both persuaded that an arbitrary and d…...
使用Node.js软件包管理器(npm)安装TypeScript
安装node.js node.js的安装很简单,这里不再赘述,如果大家有需要,可以看一下这个:https://blog.csdn.net/David_house/article/details/123218488 检验电脑上node.js是否安装成功,或者是否已经安装node.js,…...
鸿蒙ArkUI-X跨端应用开发,一套代码构建多平台应用
文章目录 一、项目介绍二、技术架构三、Gitee仓库地址四、ArkUI-X开发者文档五、快速开始——环境准备1、下载DevEco Studio,版本V4.0 Beta2以上2、打开DevEco,下载相关环境配置3、配置开发环境3.1、OpenHarmony SDK3.2、安装ArkUI-X SDK3.2、Android SD…...

【鸿蒙软件开发】ArkTS基础组件之Gauge(环形图表)、LoadingProgress(动态加载)
文章目录 前言一、Gauge环形图表1.1 子组件1.2 接口参数介绍 1.2 属性1.3 示例代码二、LoadingProgress2.1 子组件2.2 接口2.3 属性2.4 示例代码 总结 前言 Gauge:数据量规图表组件,用于将数据展示为环形图表。 LoadingProgress:用于显示加载…...
C++模板类用作参数传递
前言 在模板类<>传递参数的一种实现。记不住,以此记录。 // dome.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。 // #define _CRT_SECURE_NO_WARNINGS #include <iostream> //#include "tools.h" #include <fu…...
SQL server 代理服务启动和查看
设置重启 使用管理员权限登录到运行 SQL Server 代理服务的计算机。 打开 Windows 服务管理器。可以通过按下 Windows 键 R,然后键入 "services.msc" 并按 Enter 来打开服务管理器。 在服务列表中,找到 "SQL Server Agent" 服务&…...

单例模式详解【2023年最新】
一、单例模式概念 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点来访问该实例。它的目的是限制一个类只能创建一个对象,以确保在整个应用程序中只有一个共享的实例。 单例模式通常用于以下情况:…...
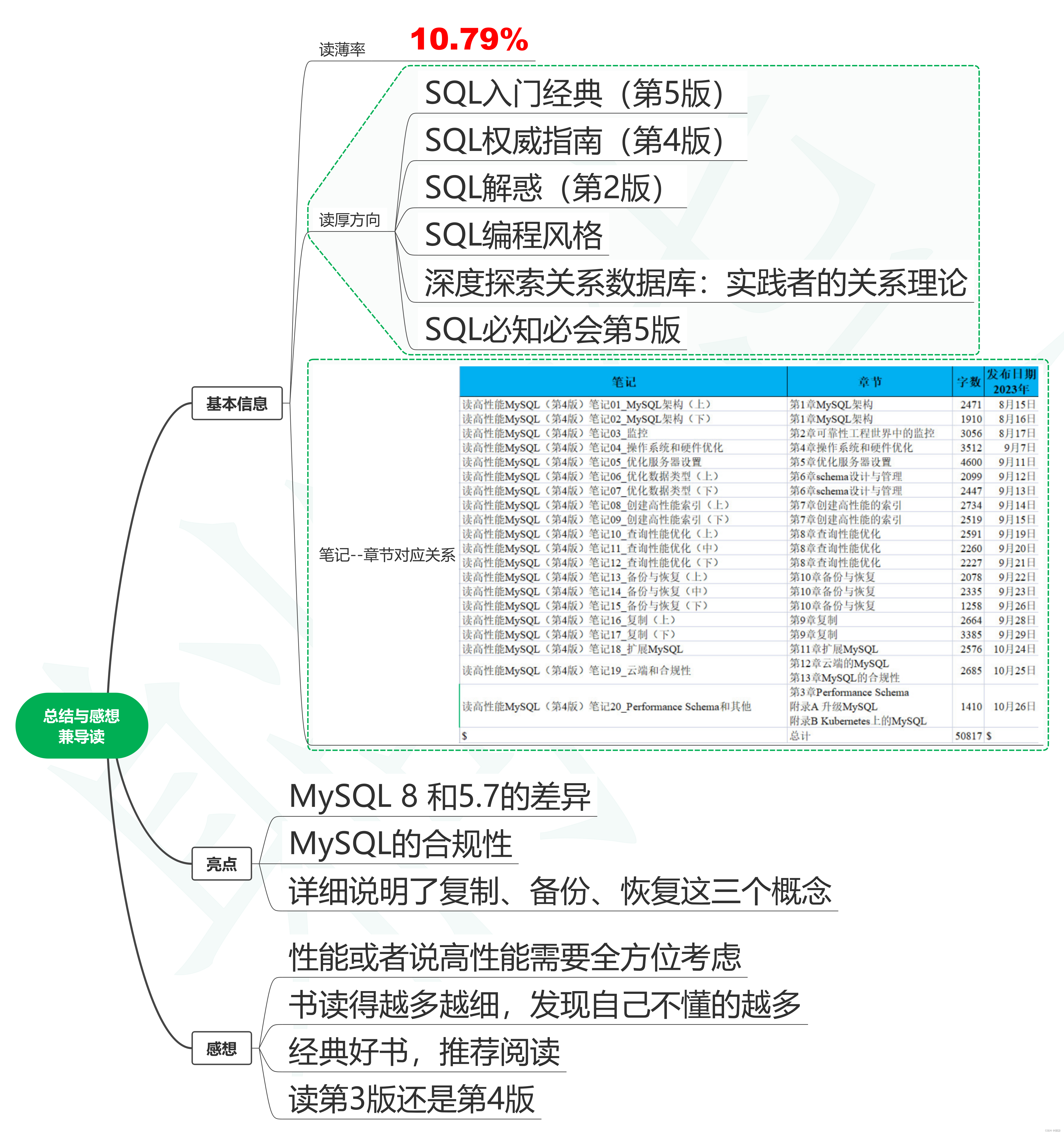
读高性能MySQL(第4版)笔记21_读后总结与感想兼导读
1. 基本信息 高性能MySQL:经过大规模运维验证的策略(第4版) High Performance MySQL, Fourth Edition [美] Silvia Botros(西尔维亚博特罗斯);Jeremy Tinley(杰里米廷利) 电子工业出版社,2022年10月出版 1.1. 读薄率 书籍总字…...

放学辣[简单版]
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 本题和 D 题的唯一区别是 NNN 的范围。 校园里目前有 NNN 名学生,这些学生属于 MMM 个班级。第 iii(i1,2,...,Ni 1,2,...,Ni1,2,...,N)个人属于第…...

面向对象设计——原型模式
原型设计模式是一种创建型设计模式,其主要目标是创建对象的新实例,同时尽量减少与使用者的交互,以降低对象创建的复杂性。这通过复制(或克隆)现有对象的实例来实现,以获得新对象,而不是通过实例化类来创建。 以下是原型设计模式的关键概念: 原型接口(Prototype Inter…...
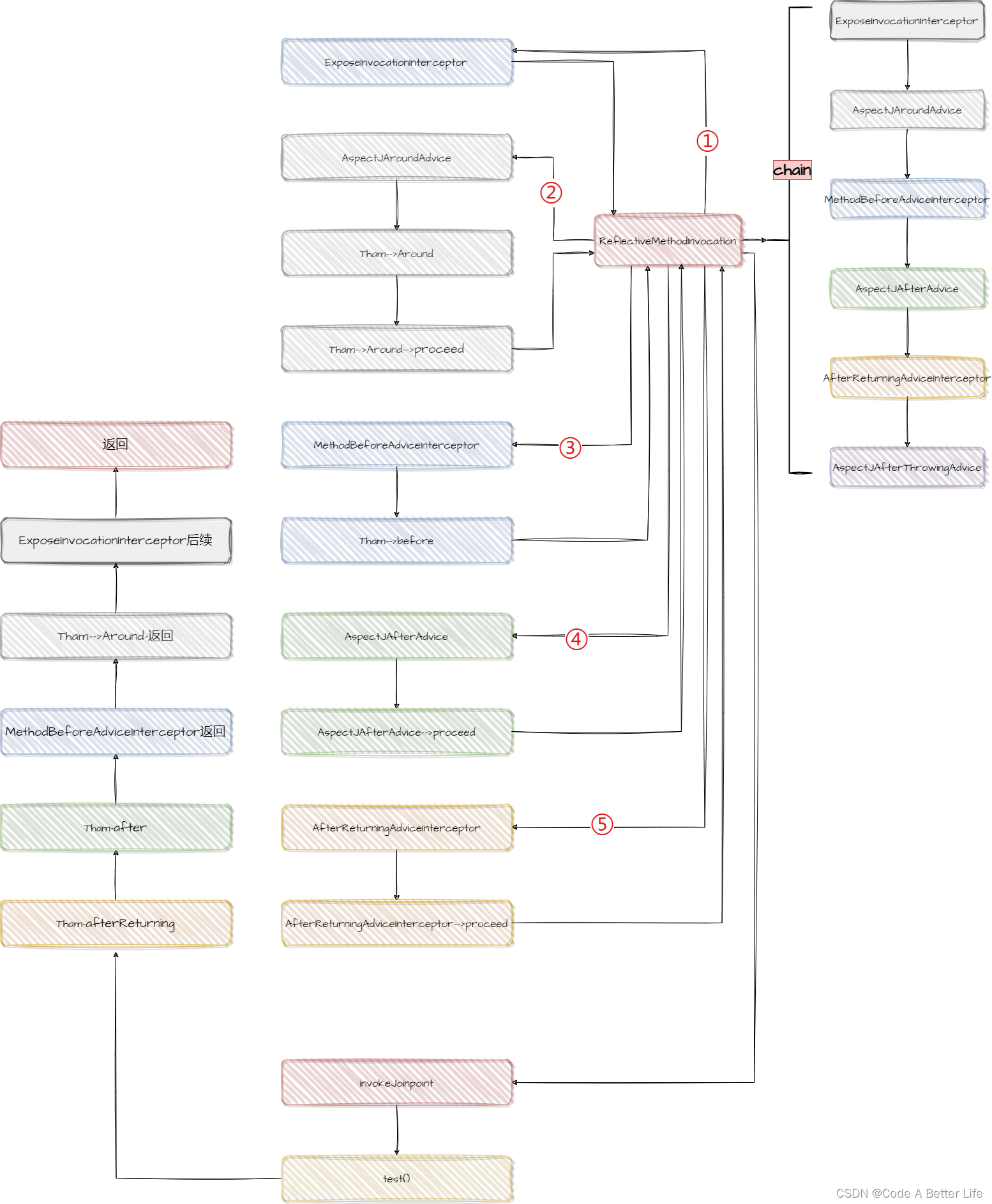
SpringAOP源码解析之advice执行顺序(三)
上一章我们分析了Aspect中advice的排序为Around.class, Before.class, After.class, AfterReturning.class, AfterThrowing.class,然后advice真正的执行顺序是什么?多个Aspect之间的执行顺序又是什么?就是我们本章探讨的问题。 准备工作 既…...

CentOS 安装 tomcat 并设置 开机自启动
CentOS 安装 tomcat 并设置 开机自启动 下载jdk和tomcat curl https://download.oracle.com/java/21/latest/jdk-21_linux-x64_bin.tar.gz curl https://dlcdn.apache.org/tomcat/tomcat-10/v10.1.15/bin/apache-tomcat-10.1.15.tar.gz解压jdk和tomcat并修改目录名称 tar -z…...

论文阅读——ELECTRA
论文下载:https://openreview.net/pdf?idr1xMH1BtvB 另一篇分析文章:ELECTRA 详解 - 知乎 一、概述 对BERT的token mask 做了改进。结合了GAN生成对抗模型的思路,但是和GAN不同。 不是对选择的token直接用mask替代,而是替换为…...
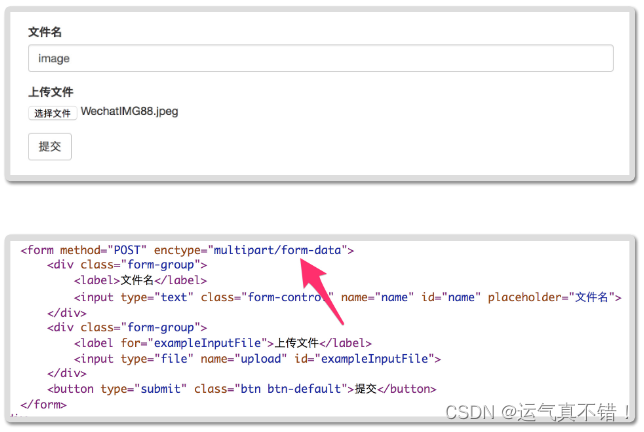
Android开发知识学习——HTTP基础
文章目录 学习资源来自:扔物线HTTPHTTP到底是什么HTTP的工作方式URL ->HTTP报文List itemHTTP的工作方式请求报文格式:Request响应报文格式:ResponseHTTP的请求方法状态码 HeaderHostContent-TypeContent-LengthTransfer: chunked (分块传…...
51单片机的hello world之点灯
文章目录 前言一、基础定义和点灯二、延时函数三、独立按键三、中断的配置和使用外部中断法捕获中断 总结 前言 hello 大家好这里是夏目学长的51单片机课堂,本篇博客是夏目学长观看B站up主学电超人的视频所写的一篇51单片机入门博客之51单片机点灯以及 独立按键 中…...
Django 实战开发(一)项目搭建
1.项目搭建 用pycharm 编辑器可以直接 New 一个 Django 项目 2.新建应用 python manage.py startapp demo项目结构如下: 3.编写第一个Django 视图函数 /demo/views: from django.http import HttpResponse def welcome(request):return HttpResponse("welcome to dja…...

Unity把余弦值转成弧度和角度
Vector3 RoleForwardV MainRole.transform.forward; Vector3 RoleToMonsterV Monster.transform.position - MainRole.transform.position; float DotResult Vector3.Dot(RoleForwardV, RoleToMonsterV.normalized);//点乘两个单位向量 Mathf.Acos(DotResult); //--它计…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
