【Hello Algorithm】滑动窗口内最大值最小值
滑动窗口介绍
滑动窗口是一种我们想象中的数据结构 它是用来解决算法问题的
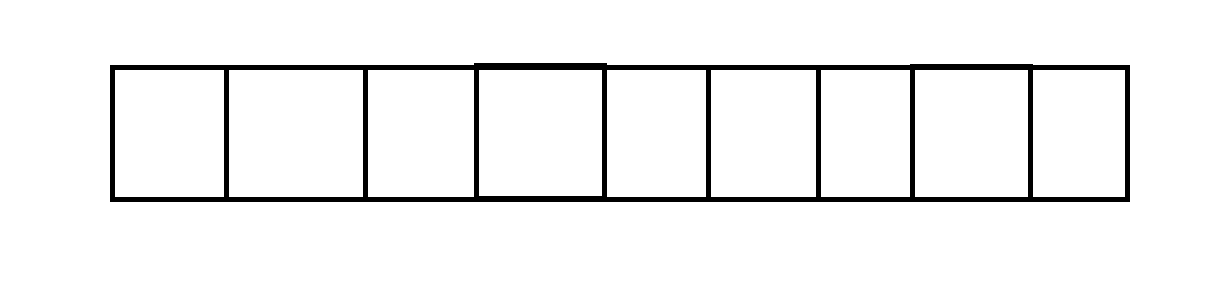
我们可以想象出一个数组 然后再在这个数组的起始位置想象出两个指针 L 和 R
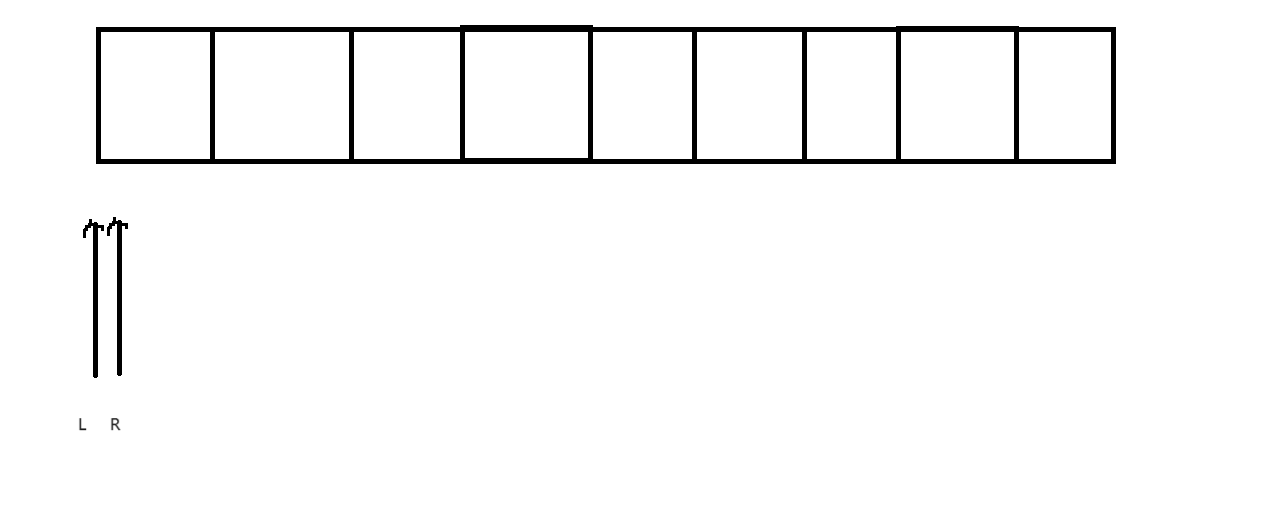
我们对于这两个指针做出以下规定
- L 和 R指针只能往右移动
- L指针不能走到R指针的右边
- 我们只能看到L指针和R指针中间的数字
比如说当前L和R指针重合 我们就什么数字都看不见
如果此时R指针往右走一步 那么我们就能看到L指针和R指针中间的数组的数字
又因为这种移动的方式特别像滑动 所以说我们将这种想象出来的数据结构叫做滑动窗口
如何确定一个滑动窗口内的最大值
如果我们每次都遍历去获取滑动窗口的最大值的话那么每次获取的时间复杂度就是O(N)了 这样子明显很复杂 所以说我们需要想想别的方式去找到最大值
这里直接给出结论:
- 我们使用双端队列去获取一个滑动窗口内的最大值
- 双端队列的意义是 : 此时开始缩小滑动窗口 哪些数字可能成为最大值
为了让双端队列能够实现它的意义 我们做出以下规定
- 让R指针向右滑动的时候 我们从右边插入数字的下标到双端队列中
- 如果说插入的数字要大于原来的数字 我们让原来的数字出队列
- 让L指针向右滑动的时候 我们从左边开始比较双端队列第一个(左边数起)下标和L指针的下标
- 如果说L指针的下标要大于双端队列最左边的下标 则将其弹出
至于C++中的双端队列 大家可以参考这篇博客 双端队列
窗口内最大值
假设一个固定大小为W的窗口 依次划过数组arr
让你依次返回每次窗口移动时窗口中的最大值
假设数组arr为 【4 , 3 , 5 ,4, 3, 3, 6, 7】 W = 3
返回【5 , 5, 5, 4, 6, 7】
这道题目实际上就是一个滑动窗口最大值的简单版本
我们使用一个双端队列就能很轻松的实现
面对这个问题我们可以拆分成两部分来解决
- 首先把滑动窗口的大小扩大到3
- 接着滑动窗口整体开始移动
两部分的代码都不算难 代码表示如下
void process5(vector<int>& arr , vector<int>& ans , int W)
{deque<int> dq(0 , 0);for (int R = 0; R < W; R++){while (!dq.empty() && arr[dq.front()] <= arr[R]){dq.pop_back();} dq.push_back(R); }
int R = W - 1; int L = 0; int N = static_cast<int>(arr.size()); while (R < N) { while (!dq.empty() && arr[dq.back()] <= arr[R]) { dq.pop_back();} dq.push_back(R);while (L > dq.front()) { dq.pop_front();} ans.push_back(arr[dq.front()]);L++; R++;}
}
这道题目给我们的提醒主要有两个
- 当我们R指针右移的时候要使用while来进行判断
- R指针在初始化之后要重置 否则会出现一些错误 为了避免这些错误 我们最好每次使用一个变量之前对其进行初始化
子数组中符合条件的个数
给定一个整形数组arr 和一个整数num
某个arr中的子数组sub 必须要满足
sub中的最大值减去sub中的最小值小于等于num
返回sub中达标的子数组的数量
我们首先分析下问题
如果我们没有学过滑动窗口和双端队列 那么这道题我们会使用暴力的方式来得到答案
三个for循环嵌套 时间复杂度就变成了n的三次方 这显然是不可以的
当我们使用滑动窗口解决这个问题的时候 由于我们的左右两个下标都是单向的往右边移动 所以说此时的时间复杂度就是N
当我们得到两个下标满足上述条件时 比如说0 ~ N上的最大值减去0~N中的最小值小于等于num
此时我们就可以说 左下标为0 右下标为0 ~ N-1上的任意一个子数组都满足条件
因为此时最大值只有可能变小 最小值只有可能变大 所以说它们之间的差值肯定还是会小于等于num
所以我们就能确定 以0为左边界 N为右边界上符合条件的子数组有 N - 0 + 1个
之后我们左边界右移即可
整体思路如下
- 我们使用两个双端队列来记录子数组的最大值和最小值
- 我们让右边界一直右移动 直到子数组不满足条件为止
- 此时通过上面的技巧计算出左边界到右边界-1的满足条件子数组个数 之后左边界++
代码表示如下
int process(vector<int>& arr, int num)
{deque<int> Max_Win(0, 0);deque<int> Min_Win(0, 0);int count = 0;int R = 0;int N = static_cast<int>(arr.size());for (int L = 0; L < N; L++){while (R < N){while (!Max_Win.empty() && arr[Max_Win.back()] <= arr[R]){Max_Win.pop_back();}Max_Win.push_back(R);while (!Min_Win.empty() && arr[Min_Win.back()] >= arr[R]){Min_Win.pop_back();}Min_Win.push_back(R);if (arr[Max_Win.front()] - arr[Min_Win.front()] > num){break;}else{R++;}}count += R - L;if (Max_Win.front() == L){Max_Win.pop_front();}if (Min_Win.front() == L){Min_Win.pop_front();}}return count;
}
这里有一点需要注意的是
count += R - L;
语句必须要放到while循环的外面才行 否则会因为R下标越界的问题而导致不会执行if语句 最终导致count计算不完整
相关文章:

【Hello Algorithm】滑动窗口内最大值最小值
滑动窗口介绍 滑动窗口是一种我们想象中的数据结构 它是用来解决算法问题的 我们可以想象出一个数组 然后再在这个数组的起始位置想象出两个指针 L 和 R 我们对于这两个指针做出以下规定 L 和 R指针只能往右移动L指针不能走到R指针的右边我们只能看到L指针和R指针中间的数字 …...

HTML,CSS实现鼠标划过头像,头像突出变大(附源码)
话不多说,先上代码 先看原图: 再看 鼠标放上去后的图: 是不是明显感觉到 人物头像突出了一些,而且还增加了阴影部分的效果呢? 直接上代码!!! <!--由于我的 img 标签放的是循环后…...

“爱知道”,你知道吗?
拥抱时代浪潮,加速科技变革。数字经济时代,杭州重点贯彻市委市政府数字经济创新提质“一号发展工程”,加快发展数字经济,推动全市数字经济往高攀升、向新进军、以融提效。基于政府对数字经济新活力的赋能、优化数字社会环节、构建…...
基于SpringBoot+Vue的服装销售系统
基于SpringBootVue的服装销售平台的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringBootMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 主页 我的订单 登录界面 管理员界面 摘要 基于SpringBoot和Vue的服装销售系统…...

针对多分类问题,使用深度学习--Keras进行微调提升性能
前面的文章对二分类问题用Keras进行了Fine-tune,使得模型的准确率进一步提升,此处对于多分类问题,尝试使用Fine-tune来提升性能。 1. 准备数据集 为了演示,本次选用了博文keras系列︱图像多分类训练与利用bottleneck features进行微调(三)中提到的数据集,原始的数据集…...

一、【Photoshop如何根据不同类型图像抠图】
文章目录 前言图形结构1、规则图形2、不规则图形 图形颜色1、轮廓清晰2、颜色分明 前言 当我们有抠图需求的时候,不要一开始就想着我怎么去把它抠出来,首先应该分析图形的特点,然后再去选取合适的工具,这样才可以做到事半功倍&am…...

rust - 理解borrow trait
简介 borrow trait 是处理借用(即其它语言中的引用)的 trait,变量的所有权不会转移.泛型定义如下: pub trait Borrow<Borrowed: ?Sized> {/// Immutably borrows from an owned value.fn borrow(&self) -> &Borrowed; }其中包含一个 borrow(&self)的方…...

review-java-basis
Path环境变量用于记住程序路径,方便在命令行窗口的任意目录启动程序 \n代表换行的意思,/t代表一个tab前进一格 强转可能导致数据的丢失(溢出) 浮点型转换为整型,直接丢掉小数部分,保留整数部分返回 数据类…...

Go 语言访问 Redis 笔记
文章目录 Mac 下载 RedisMac Redix 数据库打开服务端客户端 导包连接数据库操作字符串操作 Hash设置过期时间队列操作连接池并发操作管道化操作事务操作 Mac 下载 Redis Mac安装Redis,原来就是这么简单 Mac Redix 数据库打开 brew services start redis 服务端 …...
)
【MySQL数据库重点】第二节:MySQL基础知识(基本操作)
目录 一:数据库的操作 1.显示数据库 2.创建数据库 3.使用数据库 4.删除数据库 二:常用数据类型 1.数值类型:整型和浮点型 2.字符串类型 3.日期类型 三:表的操作 1.查看表结构 2.创建表 3.删除表 一:数据库…...

计算机网络--第一次作业
1、比较电路交换、报文交换和分组报文交换优缺点 电路交换 电路交换是以电路连接为目的的交换方式,通信之前要在通信双方之间建立一条被双方独占的物理通道(由通信双方之间的交换设备和链路逐段连接而成)。 优点: ①由于通信线路为…...

网络协议--TCP的成块数据流
20.1 引言 在第15章我们看到TFTP使用了停止等待协议。数据发送方在发送下一个数据块之前需要等待接收对已发送数据的确认。本章我们将介绍TCP所使用的被称为滑动窗口协议的另一种形式的流量控制方法。该协议允许发送方在停止并等待确认前可以连续发送多个分组。由于发送方不必…...

鼎鑫鸿鄴引入“能源互联网+”理念 打造共赢
近年来,随着全球能源消耗的不断增长和环境问题的日益突出,清洁能源转型成为全球共同关注的话题。中国作为全球最大的能源消费国,也在积极推动能源结构的优化和清洁能源的发展。鼎鑫鸿鄴新能源科技有限公司在推动清洁能源转型方面制定了一系列…...

Qt下实现支持多线程的单例模式
Qt下实现支持多线程的单例模式 Chapter1 Qt下实现支持多线程的单例模式($$$)1. 代码介绍2. 代码之路3. 详细分析3.1 什么是单例3.2 如何让类无法实例化3.3 如何调用这个唯一实例3.4 如何支持多线程3.5 如何解决内存泄漏 4. 结束语 Chapter2 Qt 全局单例类Chapter3 Qt实用技巧&a…...
基于Java的宠物商店管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding) 代码参考数据库参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者&am…...
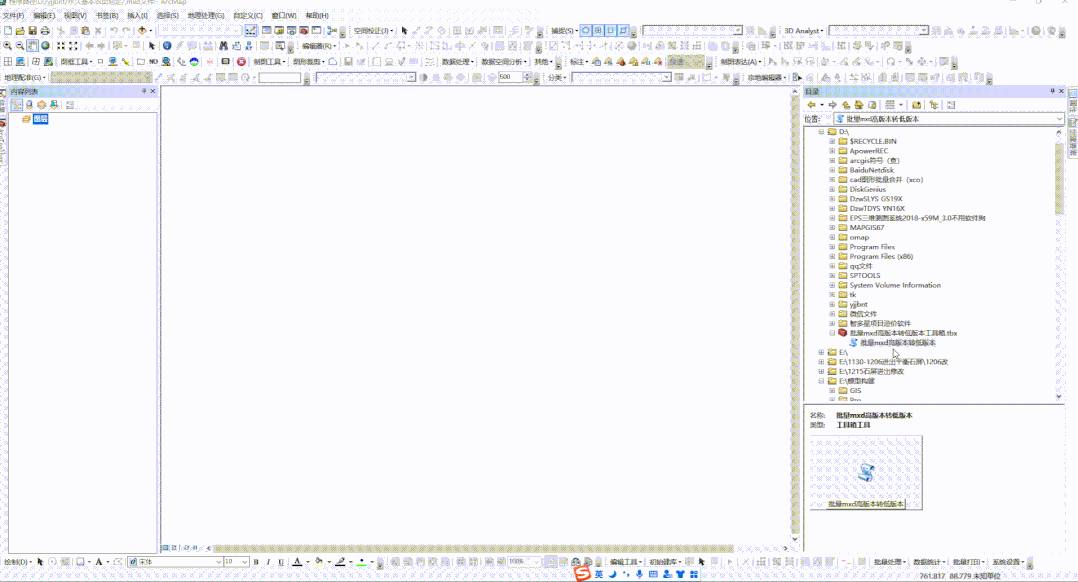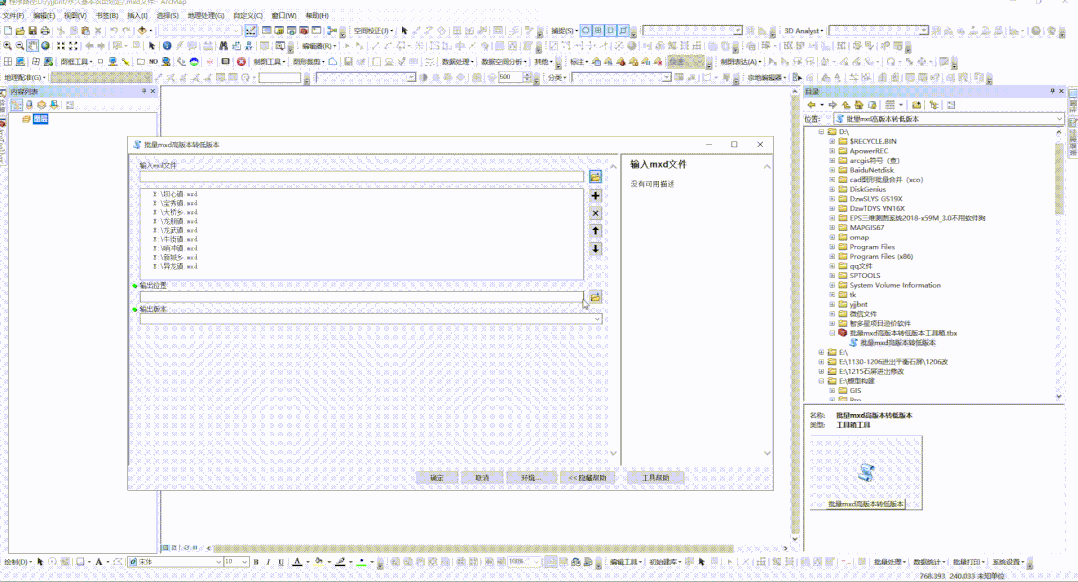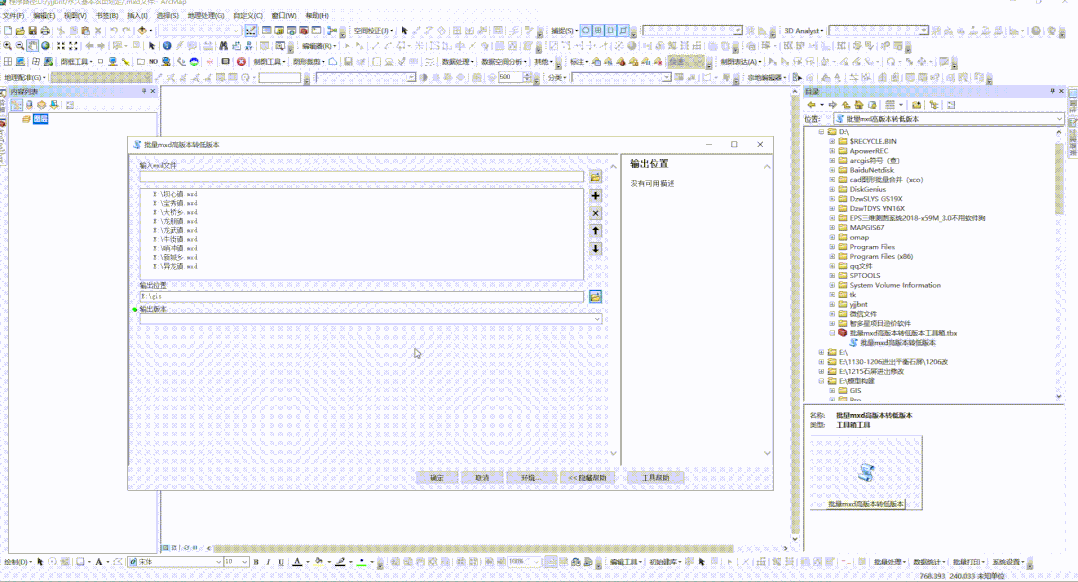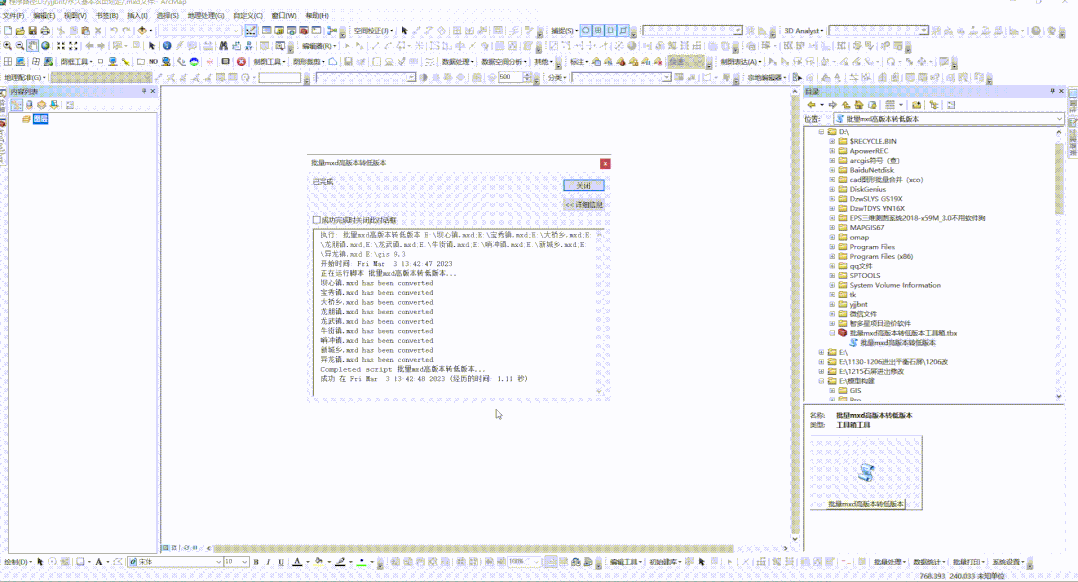
ArcGIS中批量mxd高版本转低版本
我们经常在给别人发ArcGIS的工程文件mxd,结果到别人那发现mxd工程文件打不开,原因是我们的arcgis版本高于别人,此时工程文件又很多,一个个转存成低版本又嫌麻烦,于是我们做了个批量mxd高版本转低版本的小工具ÿ…...

三篇论文:速览GPT在网络安全最新论文中的应用案例
GPT在网络安全领域的应用案例 写在最前面论文1:Chatgpt/CodeX引入会话式 APR 范例利用验证反馈LLM 的长期上下文窗口:更智能的反馈机制、更有效的信息合并策略、更复杂的模型结构、鼓励生成多样性和GPT类似的步骤:Conversational APR 对话式A…...

美术如何创建 skybox 贴图资源?
文章目录 目的PS手绘Panorama To CubemapPS手绘Pano2VRSkybox & Cubemap Tutorial (Maya & Photoshop)Unity 中使用 ReflectionProbe 生成 Cubemap 然后再 PS 调整PS直接手绘 cubemapBlender 导入 Panorama,然后烘焙到 cubemap,再导入unity中使用…...

【Linux 用户,用户组管理】
文章目录 什么是Linux用户和用户组用户(User)用户组(User Group) Linux用户和用户组管理命令1. 创建用户2. 删除用户3. 修改用户信息4. 创建用户组5. 将用户添加到用户组6. 用户和用户组的查询 用户和用户组管理实战 什么是Linux用…...
VS2022 C# 读取 excel 2023年
今天是2023年6月26日,我有一个excel表要读数据,然后放到winform程序来处理,网上的资料太旧,很多用不起来,试了一个可以使用,记录一下: 一、excel文件后缀需要小写。 二、用VS2022建一个winform…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
