学习笔记:Splay
Splay
定义
Splay 树, 或 伸展树,是一种平衡二叉查找树,它通过 Splay/伸展操作 不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,能够在均摊 O ( log n ) O(\log n) O(logn) 时间内完成插入,查找和删除操作,并且保持平衡而不至于退化为链。
Splay 树由 Daniel Sleator 和 Robert Tarjan 于 1985 年发明。
结构
节点维护信息
x tot fa[i] ch[i][0/1] val[i] cnt[i] sz[i]
根节点编号 节点个数 父亲 左右儿子编号 节点权值 权值出现次数 子树大小
struct Splay{
int fa, ch[2], val, cnt, siz;
}tree[MAXN];
操作
基本操作
maintain(x):在改变节点位置后,将节点 x x x 的 size \text{size} size 更新。
get(x):判断节点 x x x 是父亲节点的左儿子还是右儿子。
clear(x):销毁节点 x x x。
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
if(x == tree[tree[x].fa].ch[1])return true;
else return false;
}
void clear(int x){
tree[tree[x].ch[0]].siz = 0;
tree[tree[x].ch[1]].siz = 0;
tree[x].fa = 0;tree[x].val = 0;
tree[x].cnt = 0;tree[x].siz = 0;
}
旋转操作
为了使 Splay 保持平衡而进行旋转操作,旋转的本质是将某个节点上移一个位置。
旋转需要保证:
整棵 Splay 的中序遍历不变(不能破坏二叉查找树的性质)。
受影响的节点维护的信息依然正确有效。
root 必须指向旋转后的根节点。
在 Splay 中旋转分为两种:左旋和右旋。
过程
具体分析旋转步骤(假设需要旋转的节点为 x x x,其父亲为 y y y,以右旋为例)
将 y y y 的左儿子指向 x x x 的右儿子,且 x x x 的右儿子(如果 x x x 有右儿子的话)的父亲指向 y y y;ch[y][0] = ch[x][1];fa[ch[x][1]] = y;
将 x x x 的右儿子指向 y y y,且 y y y 的父亲指向 x x x;ch[x][chk^1] = y;fa[y] = x;
如果原来的 y y y 还有父亲 z z z,那么把 z z z 的某个儿子(原来 y y y 所在的儿子位置)指向 x x x,且 x x x 的父亲指向 z z z。fa[x] = z;if(z)ch[z][y == ch[z][1]] = x;
实现
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
Splay 操作
Splay 操作规定:每访问一个节点 x x x 后都要强制将其旋转到根节点。
Splay 操作即对 x x x 做一系列的 Splay 步骤。每次对 x x x 做一次 splay 步骤, x x x 到根节点的距离都会更近。定义 p p p 为 x x x 的父节点。Splay 步骤有三种,具体分为六种情况:
实现
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
插入操作
过程
插入操作是一个比较复杂的过程,具体步骤如下(假设插入的值为 k k k):
如果树空了,则直接插入根并退出。
如果当前节点的权值等于 k k k 则增加当前节点的大小并更新节点和父亲的信息,将当前节点进行 Splay 操作。
否则按照二叉查找树的性质向下找,找到空节点就插入即可(请不要忘记 Splay 操作)。
实现
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
void insert(int k){
if(!root){
tree[++tot].val = k;tree[tot].cnt++;
root = tot;maintain(root);return;
}
int cur = root, f = 0;
while(true){
if(tree[cur].val == k){
tree[cur].cnt++;
maintain(cur);maintain(f);
splay(cur);break;
}
f = cur;cur = tree[f].ch[tree[f].val < k];
if(!cur){
tree[++tot].val = k;tree[tot].cnt++;tree[tot].fa = f;
tree[f].ch[tree[f].val < k] = tot;
maintain(tot);maintain(f);splay(tot);break;
}
}
}
查询 x 的排名
过程
根据二叉查找树的定义和性质,显然可以按照以下步骤查询 x x x 的排名:
如果 x x x 比当前节点的权值小,向其左子树查找。
如果 x x x 比当前节点的权值大,将答案加上左子树( s i z e size size)和当前节点( c n t cnt cnt)的大小,向其右子树查找。
如果 x x x 与当前节点的权值相同,将答案加 1 1 1 并返回。
注意最后需要进行 Splay 操作。
实现
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
int getrank(int k){
int res = 0, cur = root;
while(true){
if(k < tree[cur].val)cur = tree[cur].ch[0];
else{
res += tree[tree[cur].ch[0]].siz;
if(k == tree[cur].val){splay(cur);return res + 1;}
res += tree[cur].cnt;cur = tree[cur].ch[1];
}
}
}
查询排名 x 的数
过程
设 k k k 为剩余排名,具体步骤如下:
如果左子树非空且剩余排名 k k k 不大于左子树的大小 s i z e size size,那么向左子树查找。
否则将 k k k 减去左子树的和根的大小。如果此时 k k k 的值小于等于 0 0 0,则返回根节点的权值,否则继续向右子树查找。
实现
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
int getval(int k){
int cur = root;
while(true){
if(tree[cur].ch[0] && k <= tree[tree[cur].ch[0]].siz)cur = tree[cur].ch[0];
else{k -= tree[tree[cur].ch[0]].siz + tree[cur].cnt;
if(k <= 0){splay(cur);return tree[cur].val;}
cur = tree[cur].ch[1];
}
}
}
查询前驱
过程
前驱定义为小于 x x x 的最大的数,那么查询前驱可以转化为:将 x x x 插入(此时 x x x 已经在根的位置了),前驱即为 x x x 的左子树中最右边的节点,最后将 x x x 删除即可。
实现
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
int getpre(){
int cur = tree[root].ch[0];
if(!cur)return cur;
while(tree[cur].ch[1])cur = tree[cur].ch[1];
splay(cur);return cur;
}
查询后继
过程
后继定义为大于 x x x 的最小的数,查询方法和前驱类似: x x x 的右子树中最左边的节点。
实现
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
int getnxt(){
int cur = tree[root].ch[1];
if(!cur)return cur;
while(tree[cur].ch[0])cur = tree[cur].ch[0];
splay(cur);return cur;
}
合并两棵树
过程
合并两棵 Splay 树,设两棵树的根节点分别为 x x x 和 y y y,那么我们要求 x x x 树中的最大值小于 y y y 树中的最小值。合并操作如下:
如果 x x x 和 y y y 其中之一或两者都为空树,直接返回不为空的那一棵树的根节点或空树。
否则将 x x x 树中的最大值 Splay \operatorname{Splay} Splay 到根,然后把它的右子树设置为 y y y 并更新节点的信息,然后返回这个节点。
删除操作
过程
删除操作也是一个比较复杂的操作,具体步骤如下:
首先将 x x x 旋转到根的位置。
如果 c n t [ x ] > 1 cnt[x]>1 cnt[x]>1(有不止一个 x x x),那么将 c n t [ x ] cnt[x] cnt[x] 减 1 1 1 并退出。
否则,合并它的左右两棵子树即可。
实现
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void clear(int x){
tree[tree[x].ch[0]].siz = 0;
tree[tree[x].ch[1]].siz = 0;
tree[x].fa = 0;tree[x].val = 0;
tree[x].cnt = 0;tree[x].siz = 0;
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
int getrank(int k){
int res = 0, cur = root;
while(true){
if(k < tree[cur].val)cur = tree[cur].ch[0];
else{
res += tree[tree[cur].ch[0]].siz;
if(k == tree[cur].val){splay(cur);return res + 1;}
res += tree[cur].cnt;cur = tree[cur].ch[1];
}
}
}
int getpre(){
int cur = tree[root].ch[0];
if(!cur)return cur;
while(tree[cur].ch[1])cur = tree[cur].ch[1];
splay(cur);return cur;
}
void remove(int k){
getrank(k);
if(tree[root].cnt > 1){tree[root].cnt–;maintain(root);return;}
if(!tree[root].ch[0] && !tree[root].ch[1]){clear(root);root = 0;return;}
if(!tree[root].ch[0]){
int cur = root;root = tree[root].ch[1];
tree[root].fa = 0;clear(cur);return;
}
if(!tree[root].ch[1]){
int cur = root;root = tree[root].ch[0];
tree[root].fa = 0;clear(cur);return;
}
int cur = root, x = getpre();
tree[tree[cur].ch[1]].fa = root;
tree[root].ch[1] = tree[cur].ch[1];
clear(cur);maintain(root);
}
实现
#include
#define MAXN 100005
using namespace std;
int n, opt, x, root, tot;
struct splay{
int fa, ch[2], val, cnt, siz;
}tree[MAXN];
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == ‘-’)t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
void write(int x){
if(x < 0){putchar(‘-’);x = -x;}
if(x >= 10)write(x/ 10);
putchar(x % 10 ^ 48);
}
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void clear(int x){
tree[tree[x].ch[0]].siz = 0;
tree[tree[x].ch[1]].siz = 0;
tree[x].fa = 0;tree[x].val = 0;
tree[x].cnt = 0;tree[x].siz = 0;
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
void insert(int k){
if(!root){
tree[++tot].val = k;tree[tot].cnt++;
root = tot;maintain(root);return;
}
int cur = root, f = 0;
while(true){
if(tree[cur].val == k){
tree[cur].cnt++;
maintain(cur);maintain(f);
splay(cur);break;
}
f = cur;cur = tree[f].ch[tree[f].val < k];
if(!cur){
tree[++tot].val = k;tree[tot].cnt++;tree[tot].fa = f;
tree[f].ch[tree[f].val < k] = tot;
maintain(tot);maintain(f);splay(tot);break;
}
}
}
int getrank(int k){
int res = 0, cur = root;
while(true){
if(k < tree[cur].val)cur = tree[cur].ch[0];
else{
res += tree[tree[cur].ch[0]].siz;
if(k == tree[cur].val){splay(cur);return res + 1;}
res += tree[cur].cnt;cur = tree[cur].ch[1];
}
}
}
int getval(int k){
int cur = root;
while(true){
if(tree[cur].ch[0] && k <= tree[tree[cur].ch[0]].siz)cur = tree[cur].ch[0];
else{k -= tree[tree[cur].ch[0]].siz + tree[cur].cnt;
if(k <= 0){splay(cur);return tree[cur].val;}
cur = tree[cur].ch[1];
}
}
}
int getpre(){
int cur = tree[root].ch[0];
if(!cur)return cur;
while(tree[cur].ch[1])cur = tree[cur].ch[1];
splay(cur);return cur;
}
int getnxt(){
int cur = tree[root].ch[1];
if(!cur)return cur;
while(tree[cur].ch[0])cur = tree[cur].ch[0];
splay(cur);return cur;
}
void remove(int k){
getrank(k);
if(tree[root].cnt > 1){tree[root].cnt–;maintain(root);return;}
if(!tree[root].ch[0] && !tree[root].ch[1]){clear(root);root = 0;return;}
if(!tree[root].ch[0]){
int cur = root;root = tree[root].ch[1];
tree[root].fa = 0;clear(cur);return;
}
if(!tree[root].ch[1]){
int cur = root;root = tree[root].ch[0];
tree[root].fa = 0;clear(cur);return;
}
int cur = root, x = getpre();
tree[tree[cur].ch[1]].fa = root;
tree[root].ch[1] = tree[cur].ch[1];
clear(cur);maintain(root);
}
int main(){
n = read();
for(int i = 1 ; i <= n ; i ++){
opt = read();x = read();
switch(opt){
case 1:insert(x);break;
case 2:remove(x);break;
case 3:write(getrank(x));putchar(‘\n’);break;
case 4:write(getval(x));putchar(‘\n’);break;
case 5:insert(x);write(tree[getpre()].val);putchar(‘\n’);remove(x);break;
case 6:insert(x);write(tree[getnxt()].val);putchar(‘\n’);remove(x);break;
default:break;
}
}
return 0;
}
Splay 操作的时间复杂度
因为 zig 和 zag 是 对称 操作,我们只需要对 zig,zig−zig,zig−zag 操作分析复杂度。采用势能分析,定义一个 n n n 个节点的 Splay 树进行了 m m m 次 Splay 步骤。可记 w ( x ) = [ log ( size ( x ) ) ] w(x)=[\log(\operatorname{size}(x))] w(x)=[log(size(x))], 定义势能函数为 φ = ∑ w ( x ) \varphi =\sum w(x) φ=∑w(x), φ ( 0 ) ≤ n log n \varphi (0) \leq n \log n φ(0)≤nlogn,在第 i i i 次操作后势能为 φ ( i ) \varphi (i) φ(i), 则我们只需要求出初始势能和每次的势能变化量的和即可。
由此可见,三种 Splay 步骤的势能全部可以缩放为 ≤ 3 ( w ′ ( x ) − w ( x ) ) \leq 3(w'(x)−w(x)) ≤3(w′(x)−w(x)). 令 w ( n ) ( x ) = w ′ ( n − 1 ) ( x ) w^{(n)}(x)=w'^{(n-1)}(x) w(n)(x)=w′(n−1)(x), w ( 0 ) ( x ) = w ( x ) w^{(0)}(x)=w(x) w(0)(x)=w(x), 假设 Splay 操作一次依次访问了 x 1 , x 2 , ⋯ , x n x_{1}, x_{2}, \cdots, x_{n} x1,x2,⋯,xn, 最终 x 1 x_{1} x1 成为根节点,我们可以得到:
3 ( ∑ i = 0 n − 2 ( w ( i + 1 ) ( x 1 ) − w ( i ) ( x 1 ) ) + w ( n ) − w ( n − 1 ) ( x 1 ) ) + 1 = 3 ( w ( n ) − w ( x 1 ) ) + 1 ≤ log n \begin{aligned} 3\left(\sum_{i=0}^{n-2}\left(w^{(i+1)}(x_{1})-w^{(i)}(x_{1})\right)+w(n)−w^{(n-1)}(x_{1})\right)+1 & = 3(w(n)−w(x_{1}))+1 \\ & \leq \log n \end{aligned} 3(i=0∑n−2(w(i+1)(x1)−w(i)(x1))+w(n)−w(n−1)(x1))+1=3(w(n)−w(x1))+1≤logn
继而可得:
∑ i = 1 m ( φ ( m − i + 1 ) − φ ( m − i ) ) + φ ( 0 ) = n log n + m log n \sum_{i=1}^m (\varphi (m-i+1)−\varphi (m−i)) +\varphi (0) = n \log n+m \log n i=1∑m(φ(m−i+1)−φ(m−i))+φ(0)=nlogn+mlogn
因此,对于 n n n 个节点的 Splay 树,做一次 Splay 操作的均摊复杂度为 O ( log n ) O(\log n) O(logn)。因此基于 Splay 的插入,查询,删除等操作的时间复杂度也为均摊 O ( log n ) O(\log n) O(logn)。
相关文章:

学习笔记:Splay
Splay 定义 Splay 树, 或 伸展树,是一种平衡二叉查找树,它通过 Splay/伸展操作 不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,能够在均摊 O ( log n ) O(\log n) O(logn) 时间内完成插入,查…...
JAVA中的垃圾回收器(1)
一)垃圾回收器概述: 1.1)按照线程数来区分: 串行回收指的是在同一时间端内只允许有一个CPU用于执行垃圾回收操作,此时工作线程被暂停,直至垃圾回收工作结束,在诸如单CPU处理器或者较小的应用内存等硬件平台不是特别优越的场合,出行…...
Windows 10/11如何恢复永久删除的文件?
数据丢失在我们的工作生活中经常发生。当你决定清理硬盘或U盘时,你会删除一些文件夹或文件。如果你通过右键单击删除文件,则可以很容易从回收站恢复已删除的文件。但是,如果你按Shift Delete键、清空回收站或删除大于8998MB的大文件夹&#…...
)
【Shell 系列教程】shell介绍(一)
文章目录 前言Shell 脚本Shell 环境第一个shell脚本运行 Shell 脚本有两种方法:1、作为可执行程序2、作为解释器参数 前言 Shell 是一个用 C 语言编写的程序,它是用户使用 Linux 的桥梁。Shell 既是一种命令语言,又是一种程序设计语言。 Sh…...

考研数学中放缩法和无穷项求和
考研数学放缩法和无穷项求和 放缩法专题例子1例子2例子3例子4例子5 放缩法专题 本文以例子为切入,对一些常用的放缩方法进行总结归纳,以期让读者对相关问题有一定的应对手段。 例子1 问题:2020年高数甲,选择题第1题。 lim …...

计算机网络常识
文章目录 1、HTTP2、HTTP状态码1xx(信息性状态码):2xx(成功状态码):3xx(重定向状态码):4xx(客户端错误状态码):5xx(服务器…...
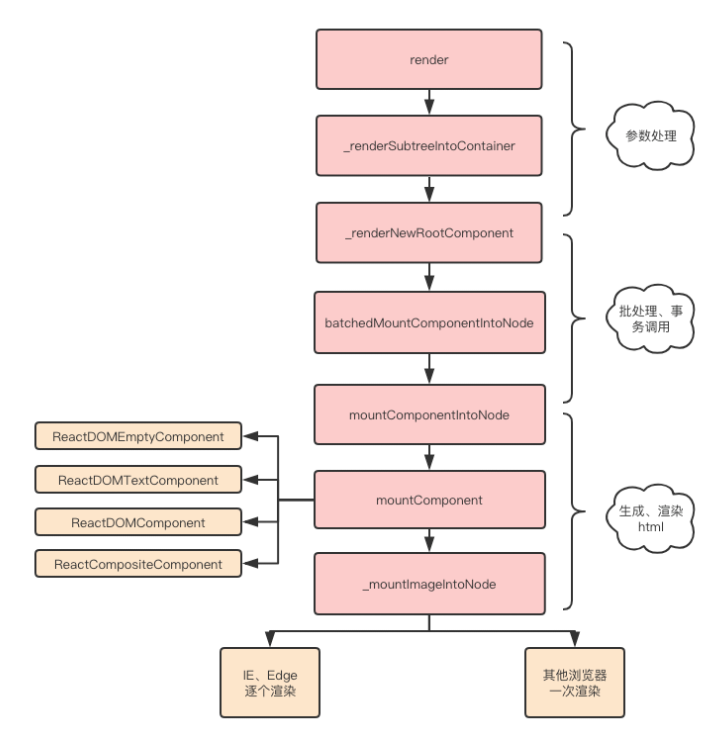
React之Jsx如何转换成真实DOM
一、是什么 react通过将组件编写的JSX映射到屏幕,以及组件中的状态发生了变化之后 React会将这些「变化」更新到屏幕上 在前面文章了解中,JSX通过babel最终转化成React.createElement这种形式,例如: <div>< img src&q…...

OpenCV学习(六)——图像算术运算(加法、融合与按位运算)
图像算术运算 6. 图像算术运算6.1 图像加法6.2 图像融合6.3 按位运算 6. 图像算术运算 6.1 图像加法 OpenCV加法是饱和运算Numpy加法是模运算 import cv2 import numpy as npx np.uint8([250]) y np.uint8([10])# OpenCV加法 print(cv2.add(x, y)) # 25010 260 > 255…...

如何做好一次代码审查,什么样是一次优秀的代码审查,静态代码分析工具有哪些
代码审查是确保代码质量、提升团队协作效率、分享知识和技能的重要过程。以下是进行优秀代码审查的一些指南: 如何做好代码审查: 理解代码的背景和目的: 在开始审查前,确保你了解这次提交的背景和目的,这有助于更准确…...

【Android】一个contentResolver引起的内存泄漏问题分析
长时间的压力测试后,系统发生了重启,报错log如下 JNI ERROR (app bug): global reference table overflow (max51200) global reference table overflow的log 08-08 04:11:53.052912 973 3243 F zygote64: indirect_reference_table.cc:256] JNI ER…...
2023年正版win10/win11系统安装教学(纯净版)
第一步:准备一个8G容量以上的U盘。 注意,在制作系统盘时会格式化U盘,所以最好准备个空U盘,防止资料丢失。 第二步:制作系统盘。 安装win10 进入windows官网 官网win10下载地址:https://www.microsoft.c…...

系统架构设计师-第11章-未来信息综合技术-软考学习笔记
未来信息综合技术是指近年来新技术发展而提出的一些新概念、新知识、新产品 信息物理系统(CPS ) ,人工智能( A l) ,机器人、边缘计算、数字孪生、云计算和大数据等技术 信息物理系统技术概述 信息物理系统的概念 信息物理系统是控制系统、嵌入式系统…...
方法详解)
Python __new__()方法详解
__new__() 是一种负责创建类实例的静态方法,它无需使用 staticmethod 装饰器修饰,且该方法会优先 __init__() 初始化方法被调用。 一般情况下,覆写 __new__() 的实现将会使用合适的参数调用其超类的 super().__new__(),并在返回之…...

虹科 | 解决方案 | 汽车示波器 索赔管理方案
索赔管理 Pico汽车示波器应用于主机厂/供应商与服务店/4S店的协作,实现产品索赔工作的高效管理;同时收集的故障波形数据,便于日后的产品优化和改进 故障记录 在索赔申请过程中,Pico汽车示波器的数据记录功能可以用于捕捉故障时的…...

详解Jmeter中的BeanShell脚本
BeanShell是一种完全符合Java语法规范的脚本语言,并且又拥有自己的一些语法和方法,所以它和java是可以无缝衔接的,学了Java的一些基本语法后,就可以来在Jmeter中写写BeanShell脚本了 在利用jmeter进行接口测试或者性能测试的时候,…...

前端和后端 优化
1.前端资源优化 1.1 html结构优化 保证简洁、清晰的html结构,减少或避免多余的html标签 使用HTML5的web语义化标签,结构清晰且利于seo css文件在head中引入,js文件放在body底部引入,这样做可以防止阻塞。另外如果有需要提前加载的…...

C++编译与运行:其二、编译期和运行期的区别
C的编译分为四步,最终生成一个可执行文件。 C的运行,就是将可执行文件交给操作系统,按照机器码逐步执行,运行功能。 先看一个非常非常有趣的例子: class Father{ public:virtual void f(){cout<<"I am fat…...
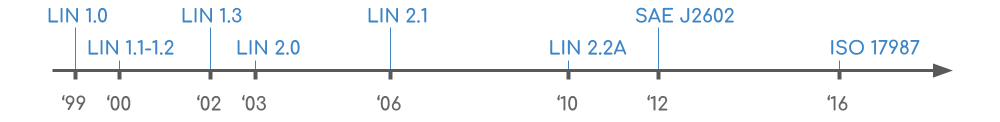
汽车电子专有名词与相应技术
1.EEA (Electronic & Electrical Architecture 电子电气架构) EEA在宏观上概括为物理架构与逻辑架构的结合,微观上通过众多电子元器件的协同配合,或集成式或分布式的系统级电子电气架构,具体详见专栏 新能源汽车电…...

idea 没加载 provided的包
目录 前言解决方案 前言 我的版本是IntelliJ IDEA 2022.1.4 (Community Edition),本地调试不知道为什么不加载provided的包。后来找到这篇文章https://youtrack.jetbrains.com/issue/IDEA-107048才知道这是个bug。不知道其他版本会不会出现这种问题。 解决方案 我…...

Hover:借贷新势力崛起,在经验与创新中找寻平衡
复苏中的Cosmos 如果让我选择一个最我感到可惜的区块链项目,我会选择Cosmos。 Cosmos最早提出并推动万链互联的概念,希望打通不同链之间的孤岛,彼时和另一个天王项目Polkadot号称跨链双雄。其跨链技术允许不同的区块链网络互相通信…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
