动态规划之01背包问题
01背包问题
- 1. 【模板】01背包
- 2. 分割等和子集
- 3. 目标和
- 4. 最后一块石头的重量 II
01背包问题是一种动态规划问题,用于求解在有限容量的背包中装入最大价值的物品组合。具体步骤如下:
- 定义一个二维数组dp[i][j],表示从前i个物品中选择若干个,放入容量为j的背包,能得到的最大价值。
- 初始化dp[0][j]和dp[i][0]为0,表示没有物品或者没有背包容量时,价值为0。遍历每个物品和每个背包容量,根据物品的重量和价值,更新dp[i][j]。有两种情况:1.如果物品i的重量大于背包容量j,那么不能放入,
dp[i][j] = dp[i-1][j],即等于前i-1个物品的最大价值。 2.如果物品i的重量小于等于背包容量j,那么可以选择放入或者不放入,dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i]),即取放入和不放入中的较大值。 - 最后返回dp[n][V],即前n个物品放入容量为V的背包的最大价值。
二维表和DP数组在背包问题中都扮演着重要的角色,但它们各自的作用是不同的。
二维表:在背包问题中,我们通常使用二维表来记录子问题的解。二维表的大小通常为(m+1) × (W+1),其中m是物品的数量,W是背包的容量。每个单元格表示对于给定的容量和物品集合,可以得到的最大价值。通过填充这个二维表,我们可以得到背包问题的最优解。
DP数组:DP数组是背包问题中最核心的部分,它用于存储每个状态的最优解。DP[i][j]代表当只有前i个物品,且背包容量为j时,可以得到的最大价值。通过填充DP数组,我们可以得到背包问题的最优解。
总的来说,二维表可以看作是DP数组的“地图”,它告诉我们应该如何填充DP数组以得到最优解。而DP数组则是实际计算最优解的地方。
1. 【模板】01背包
1.题目链接:【模板】01背包
2.题目描述:
你有一个背包,最多能容纳的体积是V。现在有n个物品,第i个物品的体积为vi ,价值为wi。
(1)求这个背包至多能装多大价值的物品?
(2)若背包恰好装满,求至多能装多大价值的物品?
输入描述:
第一行两个整数n和V,表示物品个数和背包体积。
接下来n行,每行两个数vi和wi,表示第i个物品的体积和价值。
1≤n,V,vi,wi ≤1000。
输出描述:
输出有两行,第一行输出第一问的答案,第二行输出第二问的答案,如果无解请输出0。
示例1
输入:
3 5
2 10
4 5
1 4
输出:14 9
说明:装第一个和第三个物品时总价值最大,但是装第二个和第三个物品可以使得背包恰好装满且总价值最大。
示例2
输入:
3 8
12 6
11 8
6 8
输出: 8 0
说明: 装第三个物品时总价值最大但是不满,装满背包无解。
3.问题分析:上题大概意思是对于每一个物品都有一个体积Vi和价值Wi,现在有一个背包体积为V,所以需要用两个一维数组将物品的体积和价值管理起来,然后求(1)求这个背包至多能装多大价值的物品?(2)若背包恰好装满,求至多能装多大价值的物品? 然后就按上述解法进行状态表示,该dp[i][j]表示从前i个物品中选择若干个,放入容量为j的背包,能得到的最大价值。即脑海中想象出一个二维表,该表的横坐标表示的是背包的容量V,纵坐标表示的是背包中物品的总价值W。
- 状态表示:dp[i][j]表示从前i个物品中选择若干个,放入容量为j的背包,能得到的最大价值。
- 状态转移方程:(1)求这个背包至多能装多大价值的物品?对于每一个物品来说,它只有被选择和不被选择两种结果,而选择需要先判断背包的容量够不够,所以可以先处理不选择该物品,如果不选,那么
dp[i][j] = dp[i-1][j];如果选择,则说明背包的容量可以大于该物品的体积,即j - v[i] >= 0,将该物品选择后,并且在(i-1)选择物品的前几个物品选择最大的价值,(这块如果想更好的理解,那么建议画一画dp数组)即dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])。(2)若背包恰好装满,求至多能装多大价值的物品?若背包恰好装满又该如何,那么就在加条件即可,对于第一问的dp表,可以将背包不满的位置设为-1,如果dp表某位置为-1,那么不选即可。 - 初始化:因为对于求 i,j 位置的值需要知道 i - 1,j - w[i]位置的值,根据以往的经验,可以多设置一行和一列,防止越界访问。对第一问来说,装不了的物品就dp位置设置为0,所以全部初始化为0即可。而对于第二问来说,没装满的位置设置为-1,所以需要细分一下:dp表的第一行表示的是背包的个数为0–n个,而物品的体积为0,所以除了0,0位置刚好装满其余没装满,即除了0,0位置为0,其余位置初始化为-1;dp表的第一列表示的是物品的体积为0,而背包的个数为0–n个,所以全初始化为0。
- 填表顺序:从左往右,从上到下依次填写。
- 返回值:返回dp[n][v]位置的值,第二问dp[n][v]可能是-1,所以在这判断一下,如果为-1,返回0。
4.代码如下:
#include <stdio.h>
#include <iostream>
#include <string.h>
using namespace std;const int N = 1010;
int n, V, v[N], w[N];
int dp[N][N];int main()
{cin >> n >> V;for (int i = 1; i <= n; ++i)cin >> v[i] >> w[i];for (int i = 1; i <= n; ++i){for (int j = 1; j <= V; ++j){dp[i][j] = dp[i - 1][j];if (j >= v[i])dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}cout << dp[n][V] << endl;memset(dp, 0, sizeof dp); // 将dp表进行清零for (int j = 1; j <= V; ++j)dp[0][j] = -1;for (int i = 1; i <= n; ++i){for (int j = 1; j <= V; ++j){dp[i][j] = dp[i - 1][j];if (j >= v[i] && dp[i - 1][j - v[i]] != -1)dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;return 0;
}
2. 分割等和子集
1.题目链接:分割等和子集
2.题目描述:
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
3.题目分析:这道题是将一个数组分割成两个子集,使得两个子集的元素和相等。可以这样转换一下,将这个数组求和,然后除以2求出数组的分割成两个子集的和,接下来就是在nums数组中选择一些数,使得这些被选数的和刚好等于数组总和的一半。这样这道题就是一个01背包问题。
- 状态表示:dp[i][j]表示选择前i个数中的某些值,这些数的和刚好为j。
- 状态转移方程:对于dp表的i,j位置的数来说,可能有选和不选两种结果,如果不选,那么
dp[i][j] = dp[i - 1][j];如果选的话,那么需要判断背包所剩的空间够不够选这个数,这个数在第i个位置,有j个空间,体积为nums[i],即 j > nums[i],那么dp[i][j] = max(dp[i][j], dp[i - 1][j - nums[i]]); - 初始化:和上述第二问一样,就不在解释了。
- 填表顺序:从左往右,从上到下依次填写。
- 返回值:如果dp[n][v]=-1,返回false,否则返回true。
4.代码如下:
class Solution
{
public:bool canPartition(vector<int>& nums) {int n = nums.size();int sum = 0;for (auto& x : nums)sum += x;if (sum % 2 == 1)return false;int v = sum / 2;vector<vector<int>> dp(n + 1, vector<int>(v + 1));for (int j = 1; j <= v; ++j) // 初始化dp[0][j] = -1;for (int i = 1; i <= n; ++i){for (int j = 1; j <= v; ++j){dp[i][j] = dp[i - 1][j];if (j >= nums[i - 1] && dp[i - 1][j - nums[i - 1]] != -1) // nums[i - 1]是因为增加了一行和一列,nums要对应dp的关系,所以i-1dp[i][j] = max(dp[i][j], dp[i - 1][j - nums[i - 1]]);}}if (dp[n][v] != -1)return true;elsereturn false;}
};
3. 目标和
1.题目链接:目标和
2.题目描述:
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1”。
返回可以通过上述方法构造的、运算结果等于 target 的不同。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
3.问题分析:我们需要给数组中的数添加正负号,使得它们的和等于所给的target,对于每一个数来说有正有负,那么每多一个数,就会多2^n中可能,所以不好暴力求解。但我们将nums中的正数、负数分别看作一部分,设为a,b,那么a + b = sum;a - b = target,可以算出a = (sum + target) / 2,那么是不是就可以看作是在nums数组中找一些数,使得这些数的和为a(即带正号的数),这样这道题就和上道题基本一致了。
- 状态表⽰:dp[i][j] 表⽰:在前 i 个数中选,总和正好等于 j ,⼀共有多少种选法。
- 状态转移⽅程:根据最后⼀个位置的元素,有选择最后⼀个元素或者不选择最后⼀个元素两种策略:1. 不选 nums[i] : dp[i][j] = dp[i - 1][j] ;2. 选择 nums[i] :这种情况下是有前提条件的,此时的 nums[i] 应该是⼩于等于j 。因为如果这个元素都⽐要凑成的总和⼤,选择它就没有意义呀。那么我们能够凑成总和为j 的⽅案数,就要看在前 i - 1 个元素中选,能否凑成总和为 j - nums[i] 。根据状态表⽰,此时dp[i][j] = dp[i - 1][j - nums[i]]。
- 初始化:由于需要⽤到上⼀⾏的数据,因此可以先把第⼀⾏初始化。第⼀⾏表⽰不选择任何元素,要凑成⽬标和 j 。只有0,0符合要求,所以第⼀⾏仅需初始化第⼀个元素 dp[0][0] = 1 。
- 填表顺序:
根据「状态转移⽅程」,我们需要「从上往下」填写每⼀⾏,每⼀⾏的顺序是「⽆所谓的」。 - 返回值:返回 dp[n][a] 的值。其中n 表⽰数组的⼤⼩, a表⽰要凑的⽬标和。
4.代码如下:
class Solution
{
public:int findTargetSumWays(vector<int>& nums, int target) {int n = nums.size();int sum = 0;for (auto& x : nums)sum += x;int v = (sum + target) / 2;if (v < 0 || (sum + target) % 2)return 0;vector<vector<int>> dp(n + 1, vector<int>(v + 1));dp[0][0] = 1;for(int i = 1; i <= n; i++) // 填表for(int j = 0; j <= v; j++){dp[i][j] = dp[i - 1][j];if(j >= nums[i - 1]) dp[i][j] += dp[i - 1][j - nums[i - 1]];}// 返回结果return dp[n][v];}
};
4. 最后一块石头的重量 II
1.题目链接:最后一块石头的重量 II
2.题目描述:
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释: 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],组合 7 和 8,得到 1,所以数组转为 [2,1,1,1], 组合 2 和 1,得到 1,所以数组转化为 [1,1,1], 组合 1 和1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40]
输出:5
提示:
1 <= stones.length <= 30
1 <= stones[i] <= 100
3.问题分析:将石头两两进行粉碎,两两粉碎也就是找两个数进行相减,将相减的数看作两部分,sum记为所有数的和,要使得这两部分的数尽可能的相等,那么是不是就是在所有数中,尽可能找一些数使得它们的和接近于sum的一半,这样就可以看作有一个背包,容量为sum / 2,尽可能将sum装满即可。
4.代码如下:
class Solution
{
public:int lastStoneWeightII(vector<int>& stones) {int n = stones.size();int sum = 0;for (auto& x : stones)sum += x;int v = sum / 2;vector<vector<int>> dp(n + 1, vector<int>(v + 1));for (int i = 1; i <= n; ++i){for (int j = 0; j <= v; ++j){dp[i][j] = dp[i - 1][j];if (j >= stones[i - 1])dp[i][j] = max(dp[i][j], dp[i - 1][j - stones[i - 1]] + stones[i - 1]);}}return sum - 2 * dp[n][v];}
};
相关文章:

动态规划之01背包问题
01背包问题 1. 【模板】01背包2. 分割等和子集3. 目标和4. 最后一块石头的重量 II 01背包问题是一种动态规划问题,用于求解在有限容量的背包中装入最大价值的物品组合。具体步骤如下: 定义一个二维数组dp[i][j],表示从前i个物品中选择若干个…...
安防监控项目---boa服务器的移植
文章目录 前言一、boa服务器简介二、移植步骤三、测试结果四、A9平台移植BOA总结 前言 书接上期,在配置完成环境后,那么接下来呢还得移植两个非常关键的东西,一个呢时boa服务器,另一个呢时cgi接口,boa服务器能够使得我…...

Gson 字符串常用转换方式(集合转换为Json数组
数组转换为 Json 字符串: GsonUtils.toJson(itemListBean.getImgs())json 字符串转换为数组 Gson().fromJson(goodsDbBean.getImgs(), String[].class)Json 转换为已知实体类 GsonUtils.parseJSON(result, AFileInfoBean.class);Json 转换为已知实体类集合 List<…...
)
MyBatis的使用(XML映射文件)
MyBatis的使用(XML映射文件) MyBatis基于注解开发简单便捷,但是弊端是失去SQL语句的灵活性,不能根据实际情况产生不同的SQL语句 MyBatis除了支持注解开发以外,还支持一种开发方式:XML映射文件,…...
localhost知识
文章目录 一、localhost是什么?二、localhost 在平时用到的地方三、 localhost 与 127.0.01 一、localhost是什么? localhost 是一个特殊的主机名,通常指代本机。它被用来进行本地开发和测试,也常被用作网络配置中的占位符&#…...
:神经网络-卷积层)
PyTorch入门学习(八):神经网络-卷积层
目录 一、数据准备 二、创建卷积神经网络模型 三、可视化卷积前后的图像 一、数据准备 首先,需要准备一个数据集来演示卷积层的应用。在这个示例中,使用了CIFAR-10数据集,该数据集包含了10个不同类别的图像数据,用于分类任务。…...

【EI会议征稿】 2024年遥感、测绘与图像处理国际学术会议(RSMIP2024)
2024年遥感、测绘与图像处理国际学术会议(RSMIP2024) 2024 International Conference on Remote Sensing, Mapping and Image Processing 2024年遥感、测绘与图像处理国际学术会议(RSMIP2024)将于2024年1月19日-21日在中国厦门举行。会议主要围绕遥感、测绘与图像处理等研究领…...

MySQL 8 - 处理 NULL 值 - is null、=null、is not null、<> null 、!= null
处理 NULL 值: IS NULL:IS NULL 用于检查一个列是否为 NULL。例如,如果查找一个表中某一列的值为 NULL 的行,可以使用以下语法: SELECT * FROM table_name WHERE column_name IS NULL;IS NOT NULL:IS NOT N…...
)
高教社杯数模竞赛特辑论文篇-2018年C题:大型百货商场会员画像描述(附获奖论文及MATLAB代码实现)
目录 摘 要 一、问题重述 1.1 问题背景 1.2 问题提出 二、问题分析 2.1 问题一的分析...

#力扣:2315. 统计星号@FDDLC
2315. 统计星号 - 力扣(LeetCode) 一、Java class Solution {public int countAsterisks(String s) {int cnt 0;boolean flag true;for(char c: s.toCharArray()) {if(c |) flag !flag;else if(c * && flag) cnt;}return cnt;} }...

设计模式——单例模式详解
目录 设计模式类型单例模式单例模式方式饿汉式静态常量方式静态代码块形式 懒汉式线程不安全(不推荐)懒汉式优化(不推荐) 双重检查(推荐方式)静态内部类(推荐方式)枚举方式ÿ…...

一、W5100S/W5500+RP2040树莓派Pico<静态配置网络信息>
文章目录 1. 前言2. 相关网络信息2.1 简介2.2 优点2.3 应用 3. WIZnet以太网芯片4. 静态IP网络设置示例讲解以及使用4.1 程序流程图4.2 测试准备4.3 连接方式4.4 相关代码4.5 编译烧录 5. 注意事项6. 相关链接 1. 前言 从本章开始我们将用WIZnet的W5100S/W5500以太网芯片结合RP…...
【C++的OpenCV】第十四课-OpenCV基础强化(二):访问单通道Mat中的值
🎉🎉🎉 欢迎各位来到小白 p i a o 的学习空间! \color{red}{欢迎各位来到小白piao的学习空间!} 欢迎各位来到小白piao的学习空间!🎉🎉🎉 💖💖&…...
elementUI el-collapse 自定义折叠面板icon 和 样式 或文字展开收起
: :v-deep{.el-collapse-item__arrow {width: 40px;}.el-icon-arrow-right:before {content: "展开";font-size: 15px;font-family: heiti;color: #2295ff;font-weight: bold;}.el-collapse-item__arrow.is-active {transform: none;}.el-collapse-item__arrow.is-a…...

如何用个人数据Milvus Cloud知识库构建 RAG 聊天机器人?(上)
生成式人工智能时代,开发者可以借助大语言模型(LLM)开发更智能的应用程序。然而,由于有限的知识,LLM 非常容易出现幻觉。检索增强生成(RAG)https://zilliz.com/use-cases/llm-retrieval-augmented-generation 通过为 LLM 补充外部知识,有效地解决了这一问题。 在 Chat …...

2023年江西省“振兴杯”工业互联网安全技术技能大赛暨全国大赛江西选拔赛 Write UP
文章目录 一、协议分析 - modbus二、协议分析 - 异常的流量三、协议分析 - S7Error四、协议分析 - OmronAttack五、组态编程 - 工程的秘密六、组态编程 - 工程的秘密七、组态编程 - 简单的计算八、组态编程 - 交通灯九、组态编程 - 有趣的转盘十、应急处置 - 登录日志分析十一、…...
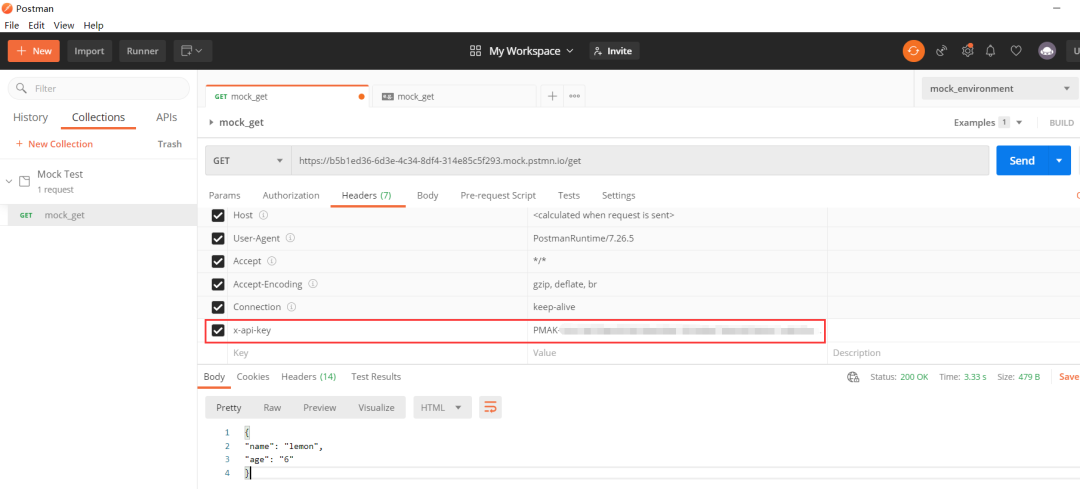
PostMan 之 Mock 接口测试
在测试的时候经常会碰到后端开发工程师的接口还没有开发完成,但是测试任务已经分配过来。没有接口怎么测试呢? 测试人员可以通过 mock server 自己去造一个接口来访问。mock server 可用于模拟真实的接口。收到请求时,它会根据配置返回对应的…...
--libgnss - NMEA数据处理)
LuatOS-SOC接口文档(air780E)--libgnss - NMEA数据处理
示例 -- 提醒: 本库输出的坐标,均为 WGS84 坐标系 -- 如需要在国内地图使用, 要转换成对应地图的坐标系, 例如 GCJ02 BD09 -- 相关链接: https://lbsyun.baidu.com/index.php?titlecoordinate -- 相关链接: https://www.openluat.com/GPS-Offset.html-- 方案1, 经lua层进行数…...

基于华为云 IoT 物联网平台实现家居环境实时监控
01 智能家居环境监测 智能家居环境监测采用 Ruff 开发板作为主控,串口线连接温湿度传感器 DHT11 和空气质量传感器 SDS011,每5分钟采集一次数据,通过 MQTT 协议发送到华为云 IoT 物联网平台,并基于数据分析服务实时计算出整个家庭…...
【开源框架】Glide的图片加载流程
本篇文章从Glide 4.11源码入手,简单的分析整个图片请求的流程,本着 ”只见树林,不见树木“ 的原则,宏观请求流程,不细究实现细节(细节留坑埋点,之后慢慢写) 引入依赖 以下的所有分…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
