服务器部署—部署springboot之Linux服务器安装jdk和tomcat【建议收藏】
我是用的xshell连接的云服务器,今天想在服务器上面部署一个前后端分离【springboot+vue】项目,打开我的云服务器才发现,过期了,然后又买了一个,里面环境啥都没有,正好出一期教程,方便大家也方便自己以后查看和回顾;这篇博客分享如何安装jdk8和tomcat8,让我们往下看;
目录
一、让我们的服务器先安装好宝塔页面
二、通过宝塔面板安装jdk
为了让更多的铁子能够接受,这里我们采取用可视化页面进行操作,也就是宝塔这个软件【不是打广告哈,确实好用😭】;
一、让我们的服务器先安装好宝塔页面
1、搜索网址来到宝塔官网宝塔面板 - 简单好用的Linux/Windows服务器运维管理面板,点击产品里面的Linux面板
2、然后点击立即免费安装

3、点击在线安装

4、会跳转到一个表单页面,输入自己ip的信息
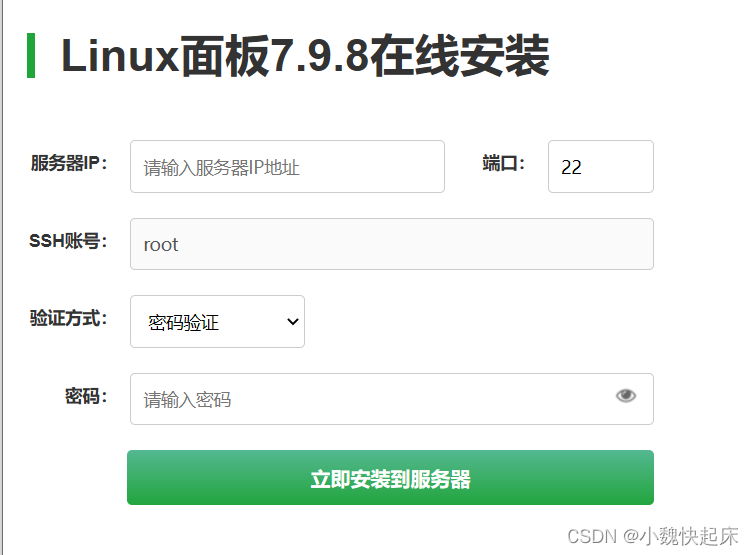
5、填写完成后,就有一个推荐套件【就是推荐你安装这些软件,比如mysql、Nginx这些后面都会用到,其他的可以不用安装,这两个留着,然后立即安装就行】
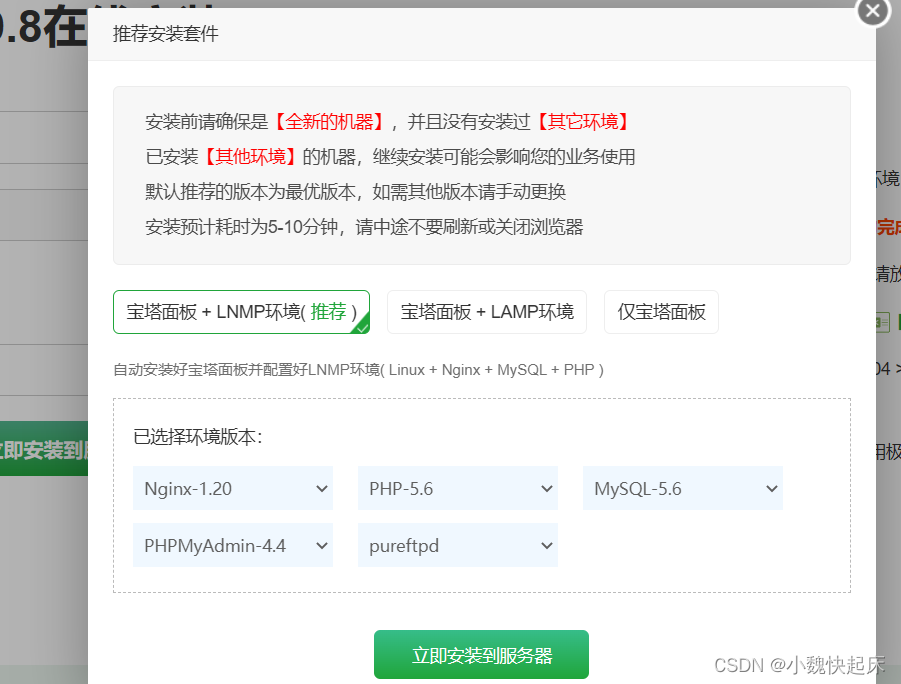
6、等待安装完成【整个过程还是要几分钟】
7、安装完成,会出现如图,这信息是登录宝塔面板用的,一定要保存好,到这里宝塔面板就安装好了;
二、通过宝塔面板安装jdk
1、登录刚刚的面板网址:例如我的是:http://112.1.1.2:8888/2a064073;
2、登录成功后,如果需要绑定手机号,直接用自己的绑定就行了,就到了我们的宝塔面板;
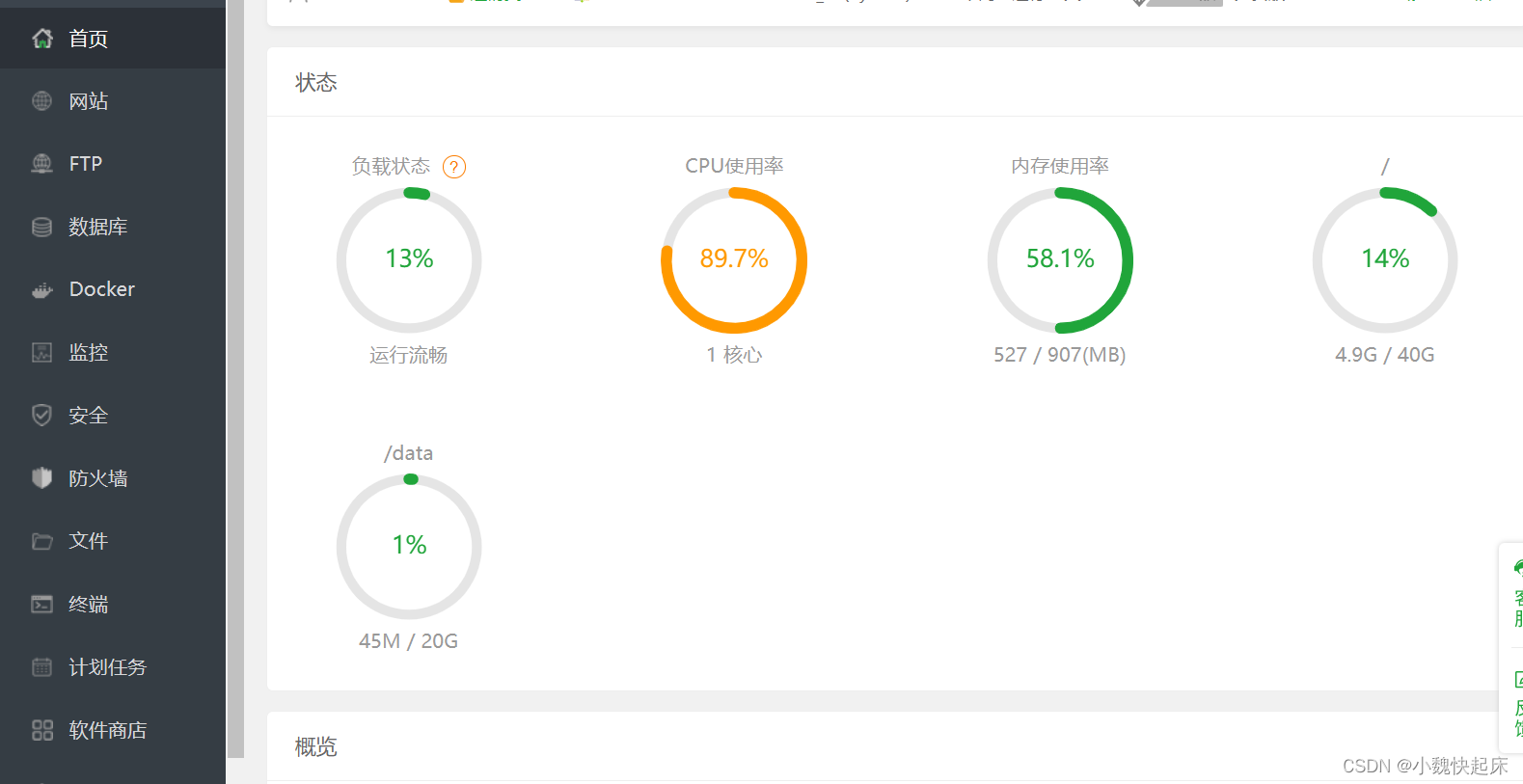
3、如下,让宝塔来安装jdk和tomcat,我们需要先安装一个工具,他来替我们安装
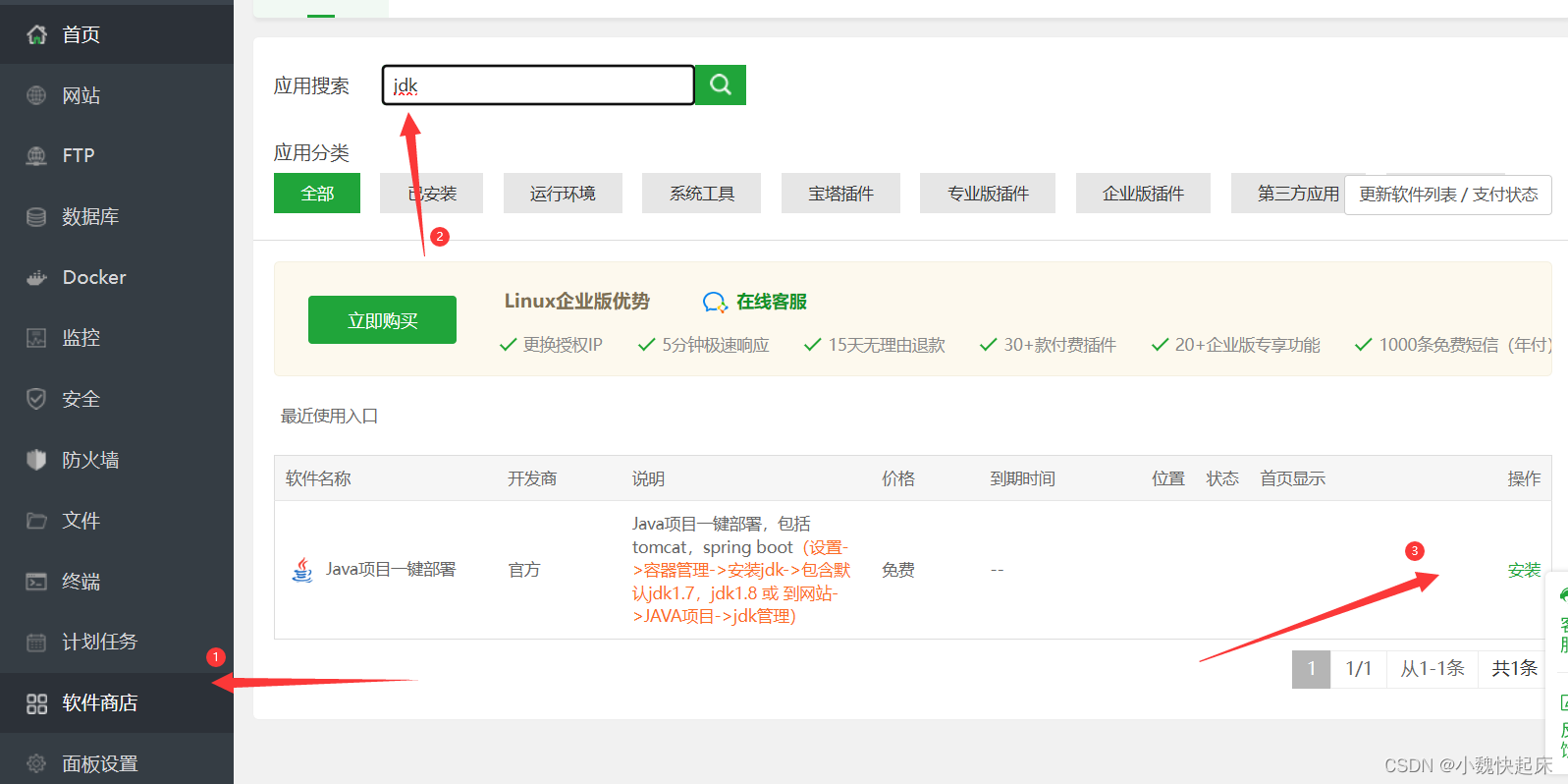

4、然后在容器管理中,我这儿选择tomcat8进行安装,然后等待完成即可
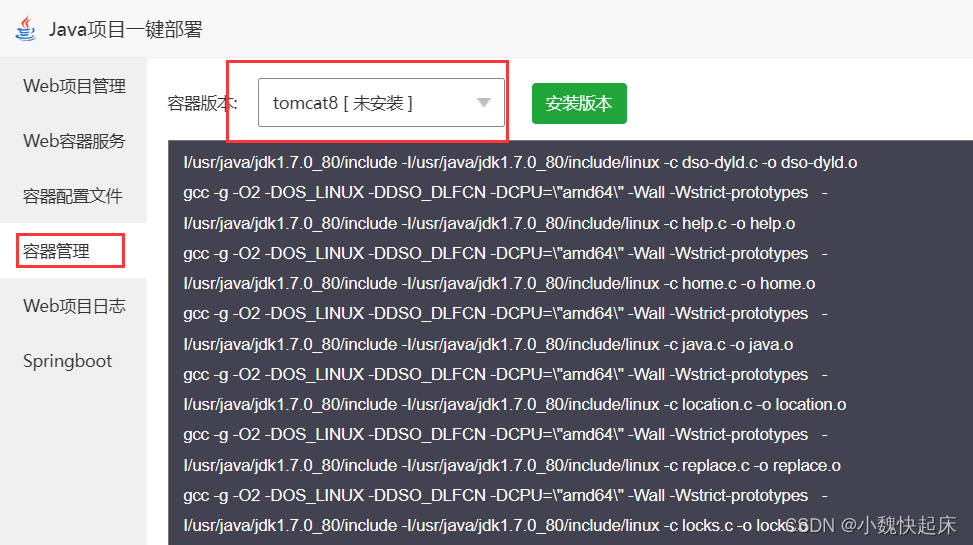
5、完成之后在ssh工具,命令行里面输入java -version即可

打完收工,看都看到这里了,更新不易,希望大家多多支持;
相关文章:

服务器部署—部署springboot之Linux服务器安装jdk和tomcat【建议收藏】
我是用的xshell连接的云服务器,今天想在服务器上面部署一个前后端分离【springbootvue】项目,打开我的云服务器才发现,过期了,然后又买了一个,里面环境啥都没有,正好出一期教程,方便大家也方便自…...

golang项目----家庭收支记账软件
家庭收支记账软件实现基本功能(先使用面向过程,后面改成面向对象)项目代码实现改进面向过程源码面向对象源码utils包中main包中实现基本功能(先使用面向过程,后面改成面向对象) 编写文件TestMyAccount.go完成基本功能 功能一:先完成可以显示…...

中国LNG市场投资机会研究
中国LNG市场投资机会研究中国LNG市场是一个具有巨大潜力和发展机遇的市场,尤其是在政府大力推动清洁能源发展的背景下,LNG市场投资机会正在不断扩大。首先,政府大力支持LNG市场的发展。政府实施的“十三五”规划将LNG作为清洁能源的重要来源&…...
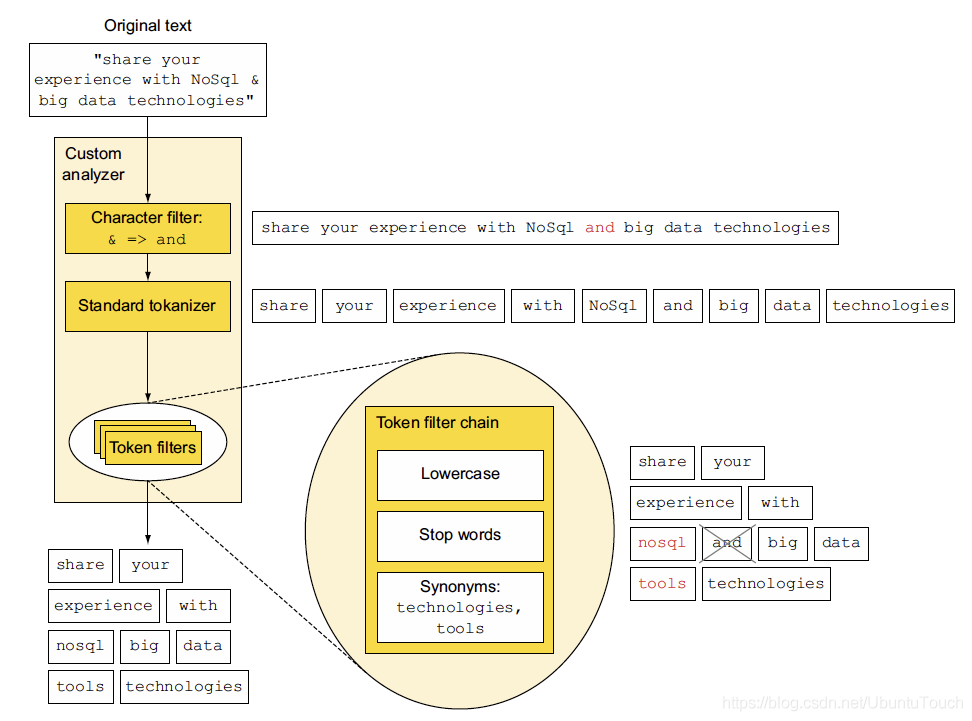
Elasticsearch:索引数据是如何完成的
在我在之前的文章 “Elasticsearch:彻底理解 Elasticsearch 数据操作” 文章中,我详细地描述了如何索引数据到 Elasticsearch 中。在今天的文章中,我想更进一步来描述这个流程。 Elasticsearch 是一个非常强大和灵活的分布式数据系统&#x…...

处理器管理
处理器状态处理器管理是操作系统中重要组成部分,负责管理、调度和分配计算机系统的重要资源——处理器,并控制程序执行由于处理器管理是操作系统最核心的部分,无论是应用程序还是系统程序,最终都要在处理器上执行以实现其功能&…...
第五)
跟着我从零开始入门FPGA(一周入门系列)第五
5、同步和异步设计 前面已有铺垫,同步就是与时钟同步。 同步就是走正步,一二一,该迈哪个脚就迈那个脚,跑的快的要等着跑的慢的。 异步就是搞赛跑,各显神通,尽最大力量去跑,谁跑得快,…...

【第42天】Arrays.sort 与 Collections.sort 应用 | 整形数组与集合的排序
本文已收录于专栏🌸《Java入门一百练》🌸学习指引序、专栏前言一.sort函数二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析三、推荐专栏序、专栏前言 本专栏开启,目的…...

LeetCode第334场周赛
2023.2.26LeetCode第334场周赛 A. 左右元素和的差值 思路 前缀和后缀和 代码 class Solution { public:vector<int> leftRigthDifference(vector<int>& nums) {int n nums.size();vector<int> l(n), r(n), ans(n);for (int i 1; i < n; i )l[…...
:PatchMatchNet配置及代码主要运行流程)
基于深度学习的三维重建网络PatchMatchNet(三):PatchMatchNet配置及代码主要运行流程
目录 1.PatchMatchNet环境配置 2. PatchMatchNet的大致执行流程(eval.py) 2.1 深度图的保存...

【一天一门编程语言】设计一门编程语言,给出基础语法代码示例,SDK设计。
文章目录设计一门编程语言,给出基础语法代码示例,SDK设计。一、编程语言设计1.1 语言名称1.2 数据类型1.3 基本运算符1.4 控制语句二、SDK设计2.1 基础库2.2 第三方库三、例子用 Mango 这门语言实现斐波那契数列。基础语法代码示例SDK 设计使用 Mango 语…...

ubuntu 下 python 安装 venv
ubuntu 下 python 安装 venv1.首先,确保您的系统已安装 Python3 和 pip3,如果没有安装,可以使用以下命令安装:2. 接着,安装 virtualenv 包,使用以下命令:3.创建 Python 虚拟环境,使用…...

HTML#1快速入门
一. 简介HTML是一门语言, 所有的网页都是用HTML编写的HTML(Hyper Text Markup Language): 超文本(超越了文本限制,除了文字信息还可以定义图片,音频,视频等)标记语言(有标签构成的语言)W3C标准: 网页主要由三部分组成(1) 结构: HTML(2) 表现: CSS(3) 行为: JavaScript二. 快速入…...
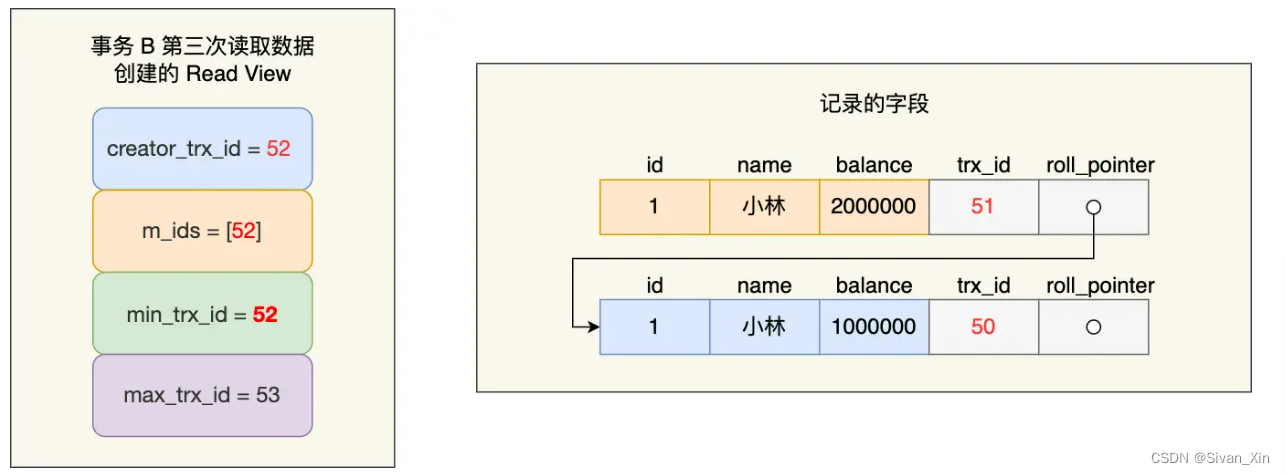
【MySQL】事务隔离级别是怎么实现的?
事务隔离级别是怎么实现的? 四种隔离级别具体的实现方式 对于「读未提交」:直接读取最新的数据就好。对于「串行化」:通过加读写锁的方式来避免并行访问。对于「读提交」和「可重复读」:通过 Read View 来实现,主要区…...
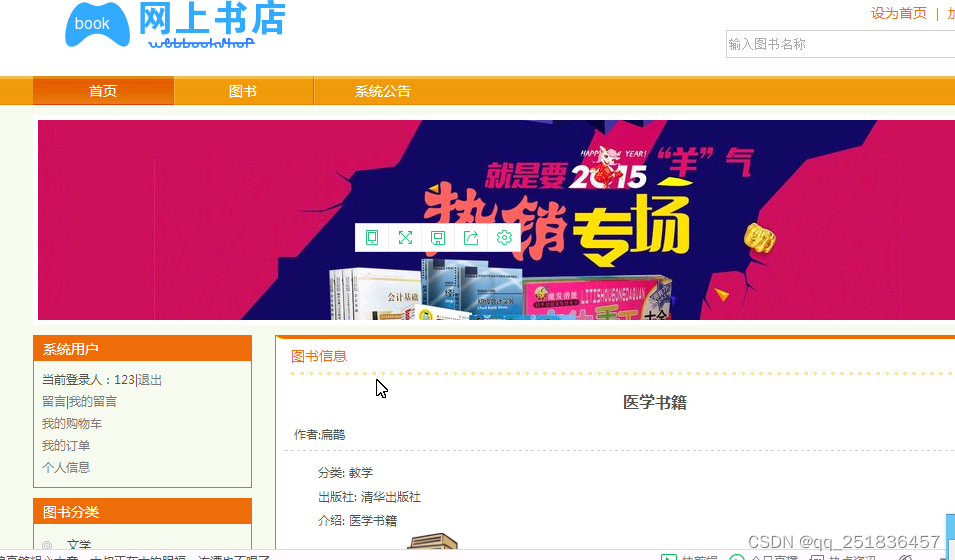
JSP网上书店系统用myeclipse定制开发mysql数据库B/S模式java编程计算机网页
一、源码特点 JSP 网上书店系统 是一套完善的系统源码,对理解JSP java 编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。研究的基本内容是基于网上书店系 统,使用JSP作为页面开发工具。Web服务的运…...

配置 Haproxy 负载均衡群集
配置 haproxy 负载均衡群集 🏆荣誉认证:51CTO博客专家博主、TOP红人、明日之星;阿里云开发者社区专家博主、技术博主、星级博主。 💻微信公众号:微笑的段嘉许 📌本文由微笑的段嘉许原创! &#…...
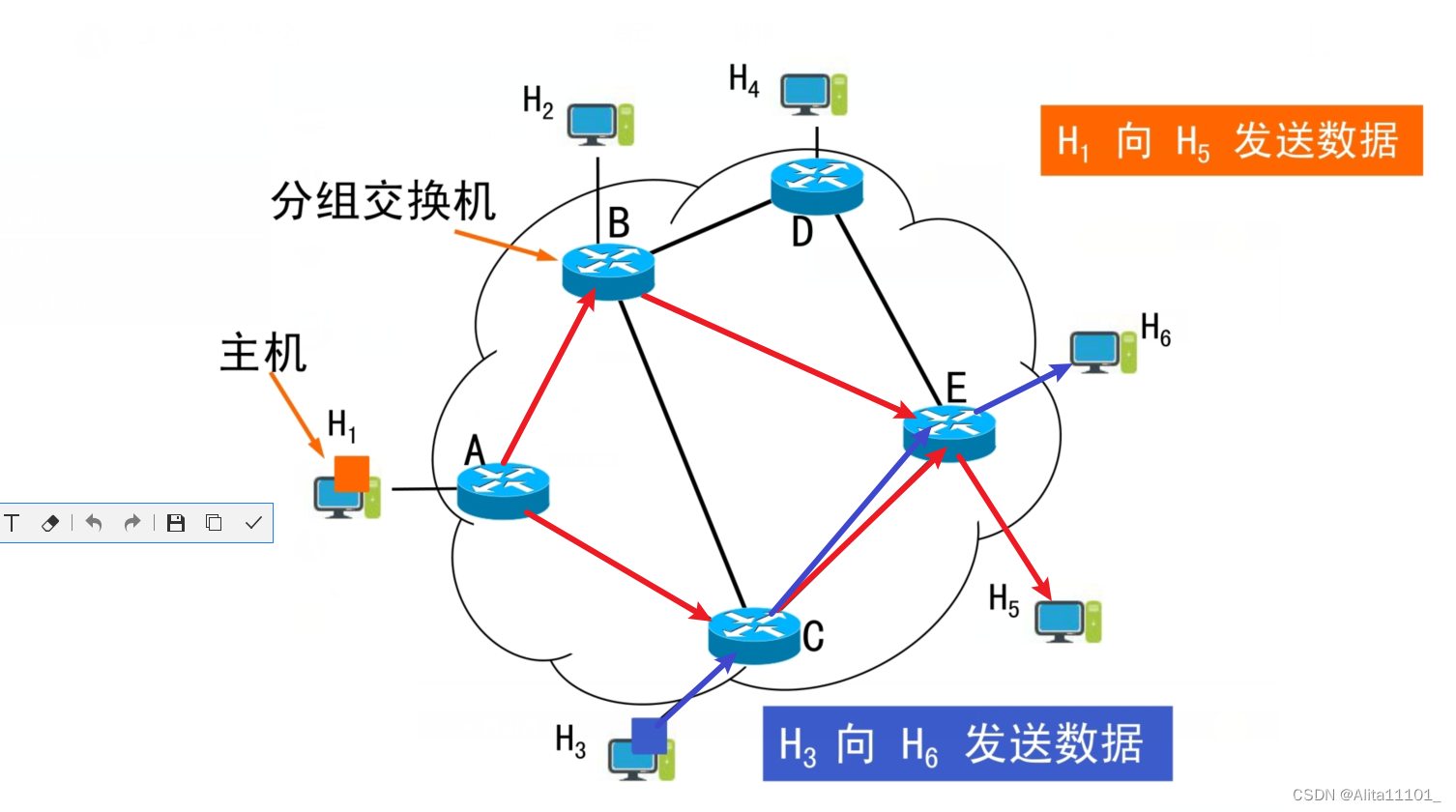
计算机网络笔记 | 第一章:计算机网络概述(1.1-1.4小节知识点整理)
从专栏将讲述有关于计算机网络相关知识点,如果有想学习Java的小伙伴可以点击下方连接查看专栏,还有JavaEE部分 本专栏地址(持续更新中):🔥计算机网络 MyBatis:✍️MyBatis Java入门篇࿱…...

Flutter3引用原生播放器-Android篇
接上篇:Flutter3引用原生播放器-IOS(Swift)篇 安卓端原生播放器的接入思路与ios基本一致,所以本篇就不废话了,直接上代码: 创建插件VideoViewPlugin实现FlutterPlugin: package io.flutter.plugins.videoplayer;imp…...
SerenityOS 操作系统类 Unix 操作系统
创建于2018年的SerenityOS是一个类似Unix的操作系统,但是带有图形化界面,适合X86台式计算机,,其界面类似90 年代的Win98/NT。几乎由一个人完成额操作系统。这几天其Web浏览器通过了 Acid3 浏览器。 Kernel features 具有抢占式多…...
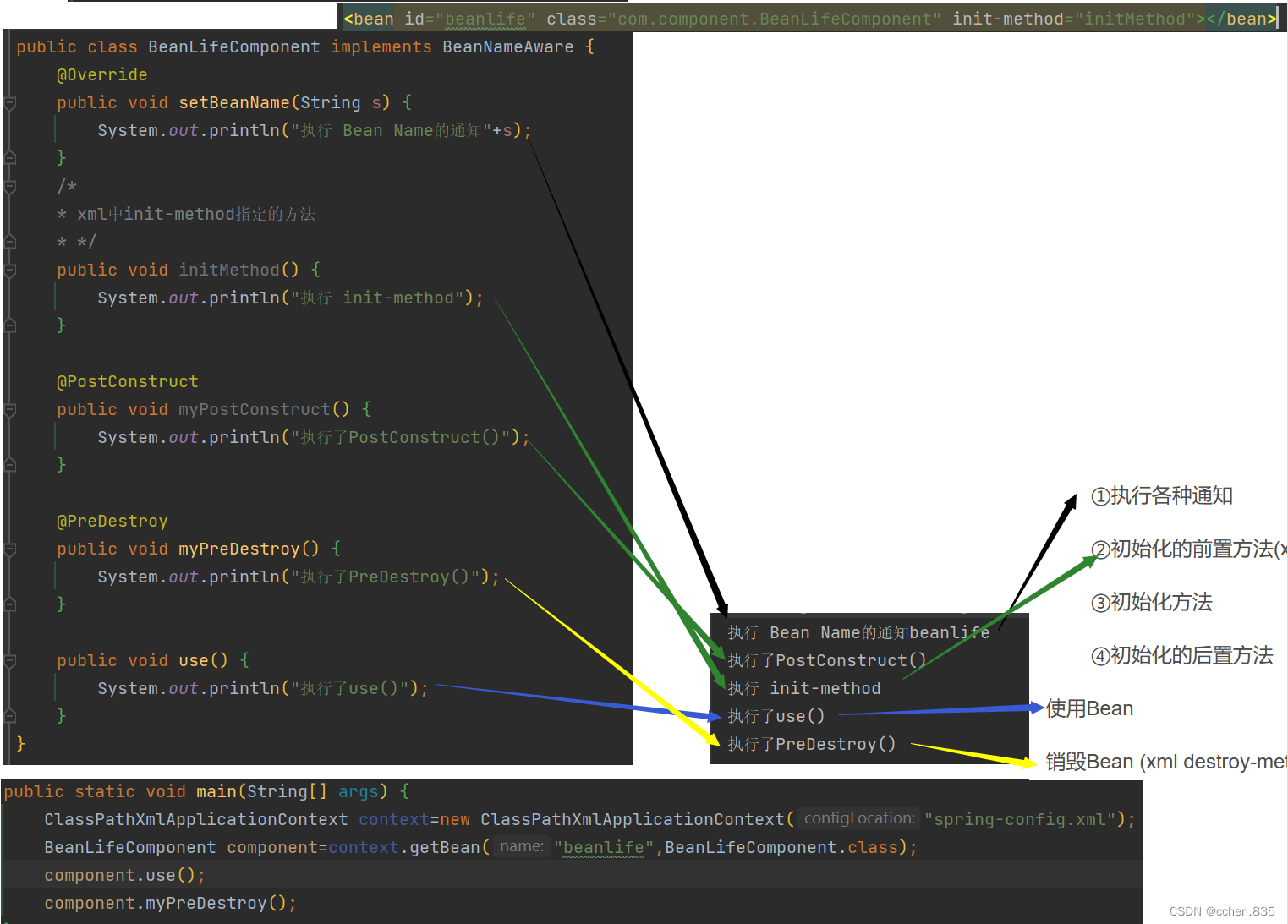
Bean作用域和生命周期
目录 Bean作用域的例子 作用域定义 Bean的六种作用域 设置作用域 Spring的执行过程和Bean的生命周期 Spring的主要执行流程 Bean的生命周期 在上篇博客中我们使用Spring存储和获取Bean,因此Bean是Spring中最重要的资源,今天这篇博客就深入了解Bean对象 Bean作用域的例子 …...
STM32笔记
目录 1.1. 预备阶段 1.2. 单片机介绍 2. 初识STM32 2.1. STM32 1.1. 预备阶段 1.2. 单片机介绍 1.2.1. 单片机是什么 单片微型计算机(Single Chip Microcomputer)简称为单片机(Microcontrollers),也称为微控制单元(Microcontroller Uni…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
