当前位置： 首页 > news >正文

Java中的QName

news 2026/2/9 14:45:22

javax.xml.namespace.QName代表XML规范中一个限定性名称（qualified name），它包含一个命名空间地址（Namespace URI）、一个本地部分、和一个前缀。QName可以用在xml的元素和属性中。
前缀提供了命名空间地址的前缀，必须和一个命名空间引用关联。它其实就是命名空间的一个占位符。
在QName.equals(Object)和QName.hashCode()函数中，只使用命名空间地址和本地部分，不会使用前缀。

例如，下面的代码片段中的QName，命名空间地址是http://ecommerce.example.org/schema，前缀是edi，本地部分是price：

  <edi:price xmlns:edi='http://ecommerce.example.org/schema' units='Euro'>32.18</edi:price>

相关文章：

Java中的QName

javax.xml.namespace.QName代表XML规范中一个限定性名称&#xff08;qualified name&#xff09;&#xff0c;它包含一个命名空间地址&#xff08;Namespace URI&#xff09;、一个本地部分、和一个前缀。QName可以用在xml的元素和属性中。 前缀提供了命名空间地址的前缀&#…...

编程日记 2023/10/29 20:29:57

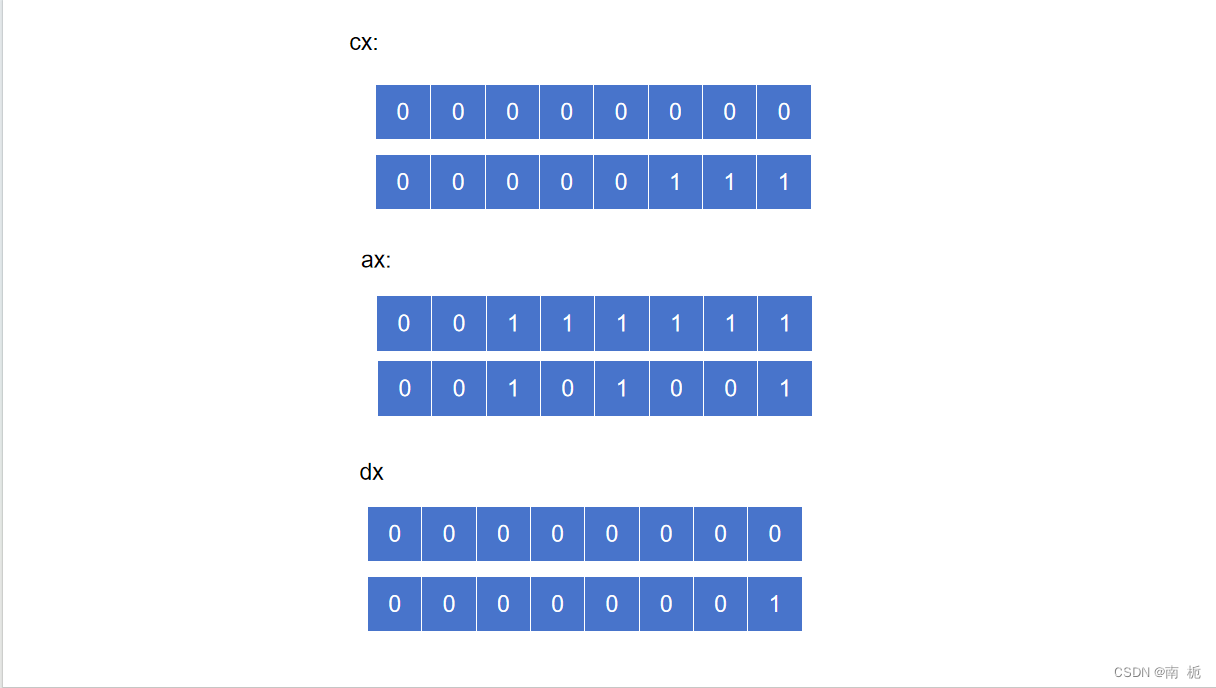
汇编语言-div指令溢出问题

汇编语言-div指令溢出问题 8086CPU中被除数保存在ax(16位)或ax和dx&#xff08;32位&#xff09;中&#xff0c;如果被除数为16位&#xff0c;进行除法运算时al保存商&#xff0c;ah保存余数。如果被除数为32位时&#xff0c;进行除法运算时&#xff0c;ax保存商&#xff0c;d…...

编程日记 2023/10/29 20:28:56

koa搭建服务器（一）

最近有个需求需要使用到koa搭建服务器并编写接口对数据库进行增删改查&#xff0c;因此写一篇博客记录这段时间的收获。 一、新建koa项目 &#xff08;一&#xff09;安装koa及其相关依赖 npm i koa npm i koa-router// 中间件&#xff0c;用于匹配路由 npm i koa-bodyparse…...

编程日记 2023/10/29 20:27:55

qt-C++笔记之在两个标签页中按行读取两个不同的文件并且滚动条自适应滚动范围高度

qt-C笔记之在两个标签页中按行读取两个不同的文件并且滚动条自适应滚动范围高度 code review! 文章目录 qt-C笔记之在两个标签页中按行读取两个不同的文件并且滚动条自适应滚动范围高度1.运行2.文件结构3.main.cc4.main.pro5.a.txt6.b.txt7.上述代码中QVBoxLayout&#xff0c…...

编程日记 2023/10/29 20:26:53

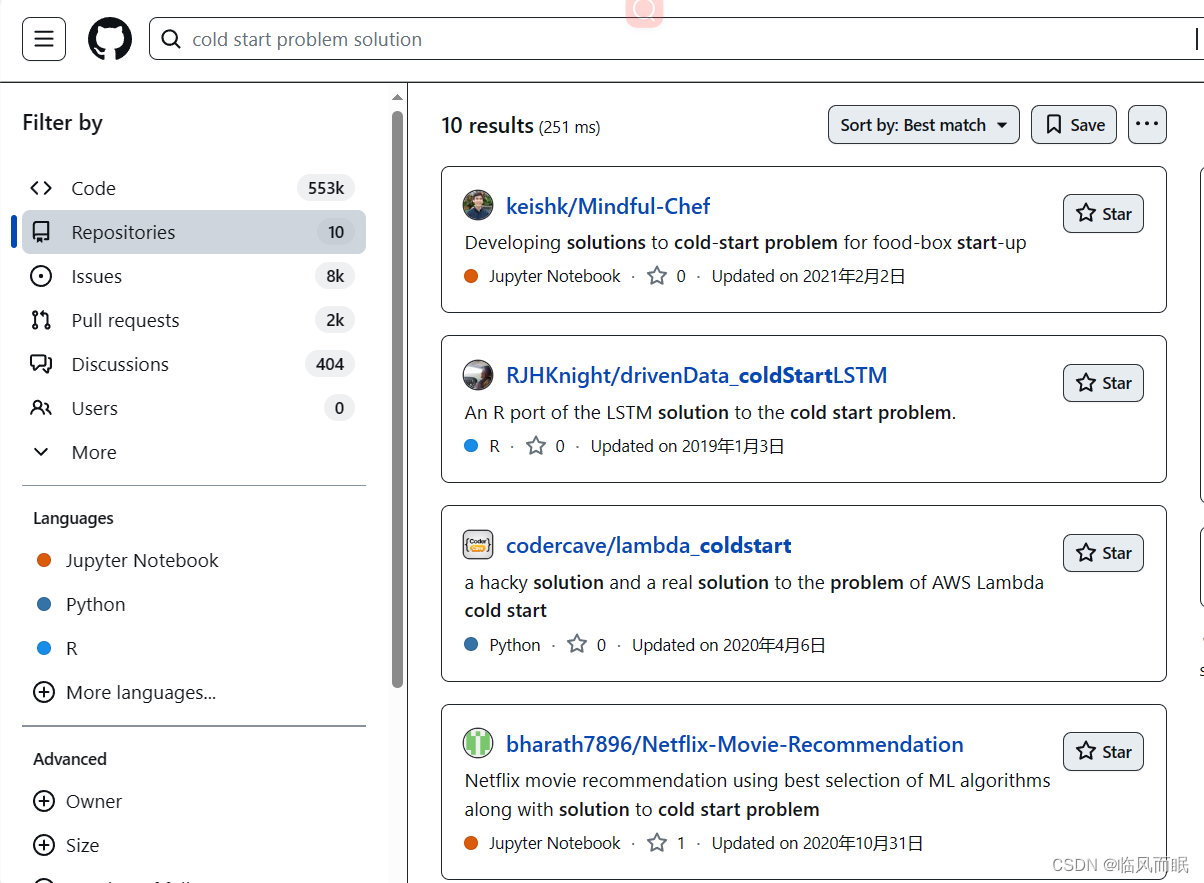
github搜索技巧探索

毕设涉及到推荐系统&#xff0c;那么就用搜索推荐系统相关资料来探索一下GitHub的搜搜技巧 文章目录 1. 基础搜索2. 限定在特定仓库搜索3. 按照语言搜索4. 按照star数量搜索5. 搜索特定用户/组织的仓库6. 查找特定文件或路径7. 按时间搜索8. 搜索不包含某个词的仓库9. 搜索特定…...

编程日记 2023/10/29 20:25:52

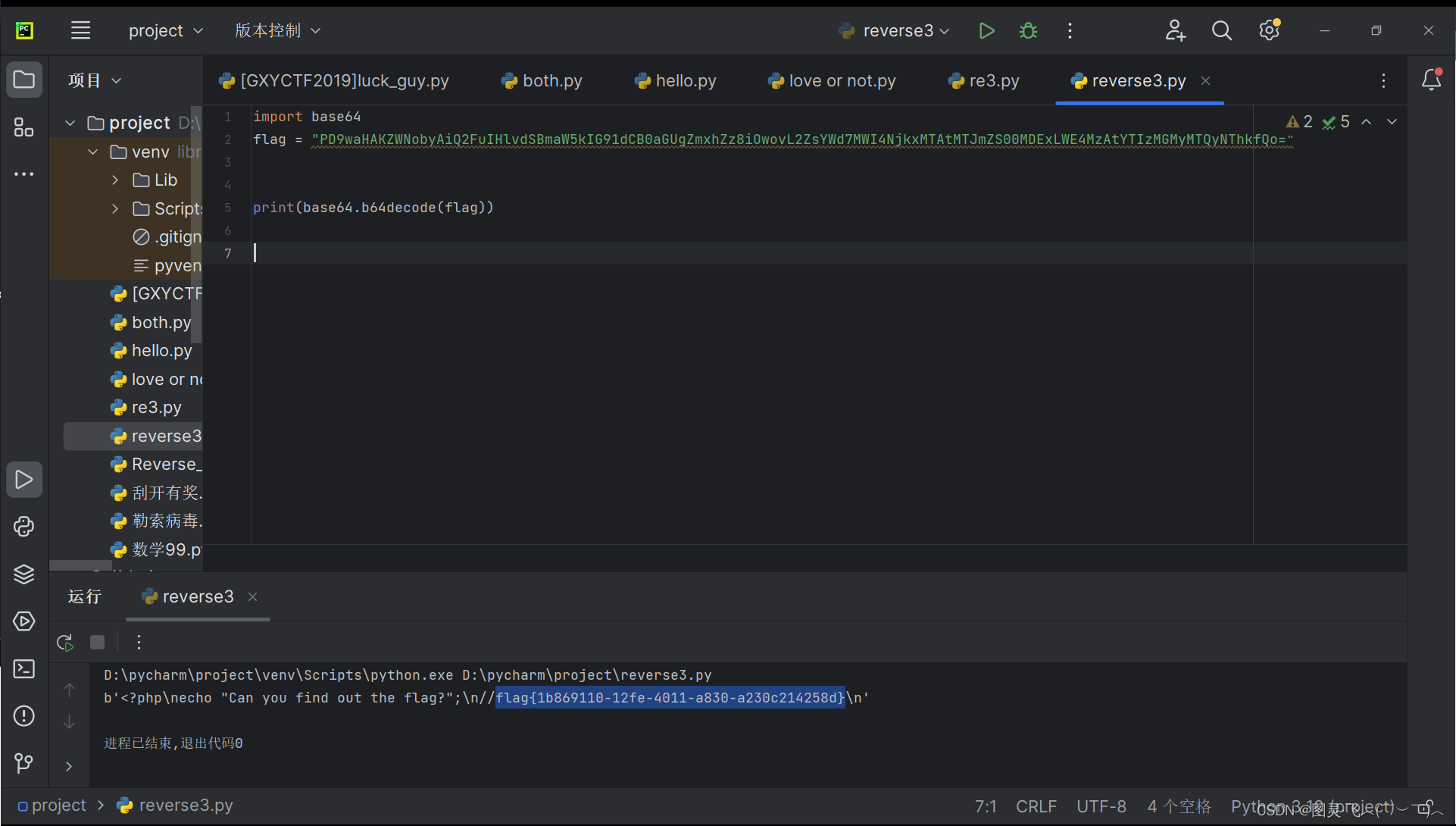
[ACTF2020 新生赛]Include

【解题思路】 1.打开链接 发现好东西&#xff0c;进一步分析。 2.分析页面 发现网页得到一个GET请求-->?fileflag.php 可以推断&#xff0c;要解答该题目需要获取 flag.php 的源代码. 将flag.php文件进行base64编码&#xff08;将网页源代码转换为Base64编码&#xff…...

编程日记 2023/10/29 20:24:51

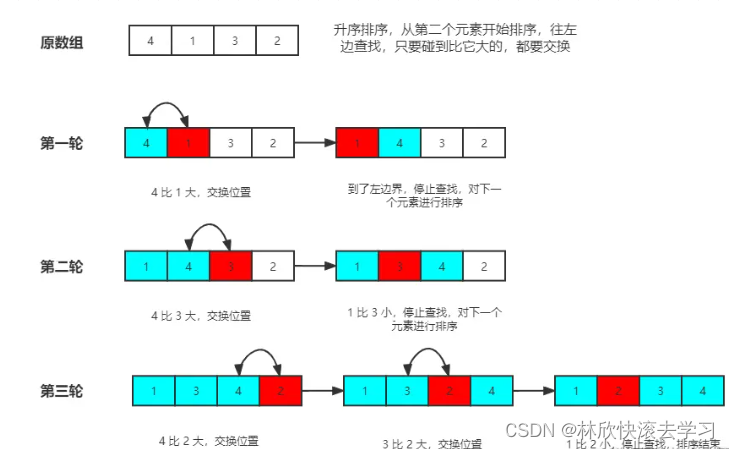
Go 实现插入排序算法及优化

插入排序 插入排序是一种简单的排序算法&#xff0c;以数组为例&#xff0c;我们可以把数组看成是多个数组组成。插入排序的基本思想是往前面已排好序的数组中插入一个元素&#xff0c;组成一个新的数组&#xff0c;此数组依然有序。光看文字可能不理解&#xff0c;让我们看看…...

编程日记 2023/10/29 20:23:50

LuatOS-SOC接口文档(air780E)--max30102 - 心率模块

max30102.init(i2c_id,int)# 初始化MAX30102传感器 参数 传入值类型 解释 int 传感器所在的i2c总线id,默认为0 int int引脚 返回值 返回值类型 解释 bool 成功返回true, 否则返回nil或者false 例子 if max30102.init(0,pin.PC05) thenlog.info("max30102&q…...

编程日记 2023/10/29 20:22:49

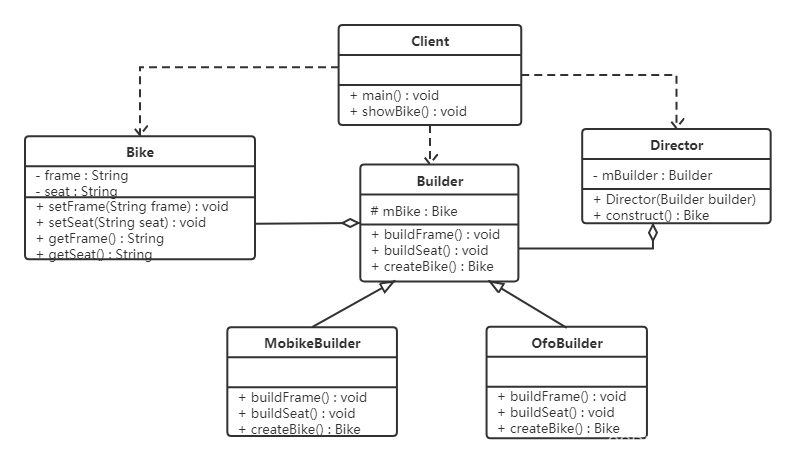
设计模式(2)-创建型模式

1&#xff0c;创建型模式 4.1 单例设计模式 单例模式&#xff08;Singleton Pattern&#xff09;是 Java 中最简单的设计模式之一。这种类型的设计模式属于创建型模式&#xff0c;它提供了一种创建对象的最佳方式。 这种模式涉及到一个单一的类&#xff0c;该类负责创建自己…...

编程日记 2023/10/29 20:21:47

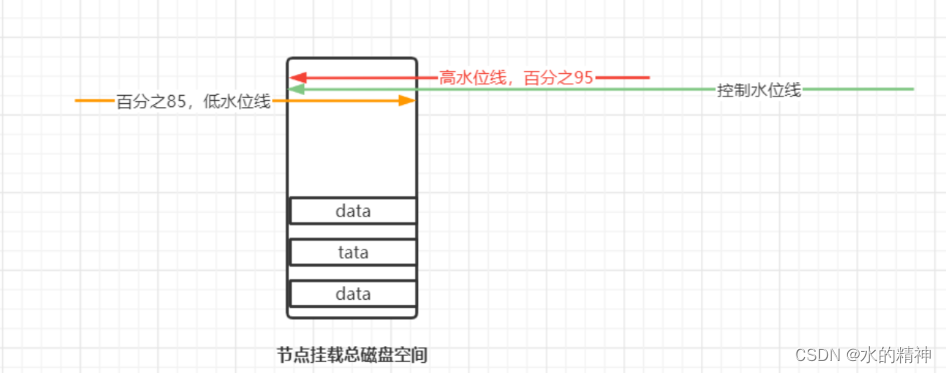
elasticsearch一些重要的配置参数

先看一下官网给我们提供的全部的参数配置项 官网地址 官方文档链接&#xff1a;注意版本是8.1Configuring Elasticsearch | Elasticsearch Guide [8.1] | Elastic​编辑https://www.elastic.co/guide/en/elasticsearch/reference/current/settings.html 重要&#xff08;基本…...

编程日记 2023/10/29 20:20:46

raft和zab算法的区别

首先&#xff0c;二者都是通过选举一个 Leader 来简化复杂度&#xff0c;后续的工作都是由 Leader 来做。 投票的时候&#xff0c;二者都需要定义一个轮次 Raft 定义了 term 来表示选举轮次 ZooKeeper 定义了 electionEpoch 来表示 同步数据的时候&#xff0c;都希望选举出来…...

编程日记 2023/10/29 20:19:44

Arthas生成火焰图命令报错汇总

操作步骤 1、在容器中集成了arthas诊断和调试工具&#xff0c;想生产火焰图&#xff0c;执行profiler start&#xff0c;报错 如下&#xff1a; [arthas1]$ profiler start AsyncProfiler error: Can not find libasyncProfiler so, please check the arthas directory. 2、…...

编程日记 2023/10/29 20:18:42

【PyQt学习篇 · ⑤】：QWidget - 鼠标操作

文章目录 鼠标形状设置常用鼠标形状设置自定义鼠标形状 重置形状获取鼠标鼠标跟踪鼠标跟踪案例 鼠标形状设置 常用鼠标形状设置 在PyQt中&#xff0c;QWidget类提供了设置鼠标形状的功能。可以使用setCursor()方法来更改QWidget及其子类的鼠标形状。该方法接受一个Qt.CursorS…...

编程日记 2023/10/29 20:17:41

2-多媒体数据压缩国际标准-Part3

文章目录 视频压缩的国际标准MPEG-1&MPEG-2/H.262视频标准MPEG-4 AVC/H.264视频标准H.264编码框架概述H.264视频编码的技术创新点 H.265/HEVC视频标准HEVC性能与编解码框架概述Quadtree-based coding structureDeblocking & SAO FilterHEVC各模块运算量 视频压缩的国际…...

编程日记 2023/10/29 20:16:40

使用Go模块进行依赖管理

摘要&#xff1a;本文将介绍Go语言中的模块&#xff08;module&#xff09;概念&#xff0c;以及如何使用Go模块进行依赖管理。我们会探讨模块的基本概念、使用方法、配置和依赖关系管理等方面的内容。 一、引言 Go语言自2007年发布以来&#xff0c;一直以其简洁、高效和强大…...

编程日记 2023/10/29 20:15:39

人工智能与航天技术的融合：未来发展的新趋势

人工智能与航天技术的融合&#xff1a;未来发展的新趋势 随着科技的飞速发展&#xff0c;人工智能和航天技术已经成为人类探索未知世界的重要工具。本文将探讨这两个领域的结合点&#xff0c;以及未来的发展趋势和应用前景。通过了解这些技术&#xff0c;读者将更好地理解人工…...

编程日记 2023/10/29 20:14:36

私有云：【11】win10安装Agent客户端组件

私有云&#xff1a;【11】win10安装Agent客户端组件 1、配置IP及加入域2、安装Agent客户端组件3、生成win10快照 1、配置IP及加入域 配置ip及dns 修改计算机名且加入域 进行验证 加入成功 将cloudadmin用户加入管理员组 输入cloudadmin户名密码验证 2、安装Agent客户端组件 …...

编程日记 2023/10/29 20:13:34

什么是程序化交易

大到量化、程序化、高频交易、套利交易、主观投资这些基本的概念&#xff0c;小到网格交易、条件单、T0、ETF套利、期现套利、算法拆单交易、打板策略等具体的投资方式。如果没有接触过这些&#xff0c;很容易混淆。 程序化交易&#xff1a; 指通过既定程序或特定软件&#xf…...

编程日记 2023/10/29 20:12:33

企业如何安全跨国传输30T文件数据

对于一些对数据敏感性比较高的企业&#xff0c;如IT企业和国企等&#xff0c;跨国数据传输是当今企业面临的一个重要挑战&#xff0c;尤其是当数据量达到30T这样的规模时&#xff0c;如何保证数据的速度、安全和合规性&#xff0c;就成为了企业必须考虑的问题。本文将从以下几个…...

编程日记 2023/10/29 20:11:32

【Linux】centos安装配置及远程连接工具的使用

&#x1f389;&#x1f389;欢迎来到我的CSDN主页&#xff01;&#x1f389;&#x1f389; &#x1f3c5;我是Java方文山&#xff0c;一个在CSDN分享笔记的博主。&#x1f4da;&#x1f4da; &#x1f31f;推荐给大家我的专栏《微信小程序开发实战》。&#x1f3af;&#x1f3a…...

编程日记 2023/10/29 20:10:31

springboot 百货中心供应链管理系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;百货中心供应链管理系统被用户普遍使用&#xff0c;为方…...

编程新知 2026/2/8 20:41:49

MFC内存泄露

1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

编程新知 2026/1/22 15:14:25

Objective-C常用命名规范总结

【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名&#xff08;Class Name)2.协议名&#xff08;Protocol Name)3.方法名&#xff08;Method Name)4.属性名&#xff08;Property Name&#xff09;5.局部变量/实例变量&#xff08;Local / Instance Variables&…...

编程新知 2025/12/14 22:33:06

2021-03-15 iview一些问题

1.iview 在使用tree组件时&#xff0c;发现没有set类的方法&#xff0c;只有get&#xff0c;那么要改变tree值&#xff0c;只能遍历treeData&#xff0c;递归修改treeData的checked&#xff0c;发现无法更改&#xff0c;原因在于check模式下&#xff0c;子元素的勾选状态跟父节…...

编程新知 2026/2/5 3:29:13

关于 WASM：1. WASM 基础原理

一、WASM 简介 1.1 WebAssembly 是什么&#xff1f; WebAssembly&#xff08;WASM&#xff09; 是一种能在现代浏览器中高效运行的二进制指令格式&#xff0c;它不是传统的编程语言&#xff0c;而是一种 低级字节码格式&#xff0c;可由高级语言&#xff08;如 C、C、Rust&am…...

编程新知 2025/11/19 10:53:07

用机器学习破解新能源领域的“弃风”难题

音乐发烧友深有体会&#xff0c;玩音乐的本质就是玩电网。火电声音偏暖&#xff0c;水电偏冷&#xff0c;风电偏空旷。至于太阳能发的电&#xff0c;则略显朦胧和单薄。 不知你是否有感觉&#xff0c;近两年家里的音响声音越来越冷&#xff0c;听起来越来越单薄&#xff1f; —…...

编程新知 2026/2/7 22:13:48

关于easyexcel动态下拉选问题处理

前些日子突然碰到一个问题&#xff0c;说是客户的导入文件模版想支持部分导入内容的下拉选&#xff0c;于是我就找了easyexcel官网寻找解决方案&#xff0c;并没有找到合适的方案&#xff0c;没办法只能自己动手并分享出来&#xff0c;针对Java生成Excel下拉菜单时因选项过多导…...

编程新知 2026/2/6 11:08:25

【若依】框架项目部署笔记

参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作&#xff1a; 压缩包下载&#xff1a;http://download.redis.io/releases 1. 上传压缩包&#xff0c;并进入压缩包所在目录&#xff0c;解压到目标…...

编程新知 2026/2/4 19:11:52

ArcPy扩展模块的使用(3)

管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如&#xff0c;可以更新、修复或替换图层数据源&#xff0c;修改图层的符号系统&#xff0c;甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

编程新知 2025/10/2 7:24:40

【Qt】控件 QWidget

控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态&#xff1a;enabled几何&#xff1a;geometrywindows frame 窗口框架的影响 窗口标题&#xff1a;windowTitle窗口图标&#xff1a;windowIconqrc 机制 窗口不透明度&#xff1a;windowOpacity光标&#xff1a;cursor…...

编程新知 2026/2/4 22:53:39