【C++代码】爬楼梯,不同路径,整数拆分,不同搜索树,动态规划--代码随想录
-
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的,例如:有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。动态规划中dp[j]是由dp[j-weight[i]]推导出来的,然后取max(dp[j], dp[j - weight[i]] + value[i])。但如果是贪心呢,每次拿物品选一个最大的或者最小的就完事了,和上一个状态没有关系。
-
状态转移公式(递推公式)是很重要,但动规不仅仅只有递推公式。对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定 dp 数组(dp table)以及下标的含义
- 确定递推公式
- dp 数组如何初始化
- 确定遍历顺序
- 举例推导 dp 数组
-
**因为一些情况是递推公式决定了dp数组要如何初始化!**写动规题目,代码出问题很正常!找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!一些同学对于dp的学习是黑盒的状态,就是不清楚dp数组的含义,不懂为什么这么初始化,递推公式背下来了,遍历顺序靠习惯就是这么写的,然后一鼓作气写出代码,如果代码能通过万事大吉,通过不了的话就凭感觉改一改。
题目:斐波那契数
-
斐波那契数 (通常用
F(n)表示)形成的序列称为 斐波那契数列 。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0) = 0,F(1) = 1; F(n) = F(n - 1) + F(n - 2),其中 n > 1 -
class Solution { public:int fib(int n) {if(n<2){return n;}int res=fib(n-1)+fib(n-2);return res;} }; -
时间复杂度:O(2^n);空间复杂度:O(n),算上了编程语言中实现递归的系统栈所占空间
-
动态规划:这里我们要用一个一维 dp 数组来保存递归的结果;确定dp数组以及下标的含义,dp[i]的定义为:第i个数的斐波那契数值是dp[i]
- 确定递推公式:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
- dp数组如何初始化:dp[0] = 0; dp[1] = 1;
- 确定遍历顺序:从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
- 举例推导dp数组
-
class Solution { public:int fib(int n) {if(n<2){return n;}vector<int> dp(n+1,0);dp[1]=1;for(int i=2;i<dp.size();i++){dp[i]=dp[i-1]+dp[i-2];}return dp[dp.size()-1];} }; -
时间复杂度:O(n); 空间复杂度:O(n)
-
if(n<2){return n;}int dp[2]={0,1};for(int i=2;i<n+1;i++){dp[i%2]=dp[0]+dp[1];}return dp[(n)%2]; -
时间复杂度:O(n);空间复杂度:O(1)
题目:爬楼梯
-
假设你正在爬楼梯。需要
n阶你才能到达楼顶。每次你可以爬1或2个台阶。你有多少种不同的方法可以爬到楼顶呢? -
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。此时大家应该发现了,这不就是斐波那契数列么!
-
class Solution { public:int climbStairs(int n) {if(n<3){return n;}int dp[2]={1,2};for(int i=2;i<n;i++){dp[i%2]=dp[0]+dp[1];}return dp[(n-1)%2];} }; -
后面将讲解的很多动规的题目其实都是当前状态依赖前两个,或者前三个状态,都可以做空间上的优化,但我个人认为面试中能写出版本一就够了哈,清晰明了,如果面试官要求进一步优化空间的话,我们再去优化。
题目:使用最小花费爬楼梯
-
给你一个整数数组
cost,其中cost[i]是从楼梯第i个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。你可以选择从下标为0或下标为1的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。- 确定dp数组以及下标的含义:本题只需要一个一维数组dp[i]就可以了。dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
- 确定递推公式:可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
- dp数组如何初始化:看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。所以初始化 dp[0] = 0,dp[1] = 0;
-
class Solution { public:int minCostClimbingStairs(vector<int>& cost) {if(cost.size()<3){return min(cost[0],cost[1]);}vector<int> dp(cost.size()+1,0);for(int i=2;i<dp.size();i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.size()];} };
题目:不同路径
-
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径? -
这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
-
class Solution { public:int track(int i,int j,int m,int n){if(i>m||j>n){return 0;}if(i==m && j==n){return 1;}return track(i+1,j,m,n)+track(i,j+1,m,n);}int uniquePaths(int m, int n) {return track(0,0,m-1,n-1);} };//超时 -
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已);深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
-
动态规划:机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
- 确定dp数组(dp table)以及下标的含义:dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式:想要求dp[i ][ j],只能有两个方向来推导出来,即dp[i - 1] [j] 和 dp[i] [j - 1]。那么很自然,dp[i][j] = dp[i - 1] [j] + dp[i] [j - 1],因为dp[i][j]只有这两个方向过来。
- dp数组的初始化:首先dp[i] [0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0] [j]也同理。
- 确定遍历顺序:dp[i] [j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
-
class Solution { public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m,vector<int>(n,1));for(int i=1;i<m;i++){for(int j=1;j<n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m-1][n-1];} }; -
时间复杂度:O(m × n);空间复杂度:O(m × n)
-
一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。那么这就是一个组合问题了。求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子,分母都算出来再做除法。需要在计算分子的时候,不断除以分母,代码如下:
-
class Solution { public:int uniquePaths(int m, int n) {long long son=1;int mom=m-1;int count=m-1;int t=m+n-2;while(count--){son *= t--;while(mom!=0 && son%mom==0){son /= mom; mom--;}}return son;} };
-
题目:不同路径 II
-
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?网格中的障碍物和空位置分别用1和0来表示。 -
数论解决,完全不行,不止一块障碍物
-
class Solution { public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int flag =0;int temp_m=0,temp_n=0;for(int i=0;i<obstacleGrid.size();i++){for(int j=0;j<obstacleGrid[0].size();j++){if(obstacleGrid[i][j]){temp_m=i;temp_n=j;flag=1;break;}}}int count_sum=obstacleGrid.size()-1;long long son_sum=1;int mom_sum=obstacleGrid.size()-1;int mn=obstacleGrid.size()+obstacleGrid[0].size()-2;while(count_sum--){son_sum *= mn--;while(mom_sum!=0 && son_sum%mom_sum==0){son_sum /= mom_sum;mom_sum--;}}if(flag==0){return son_sum;}long long son1=1;int mom1 = temp_m;int count =temp_m;int mn1 = temp_m+temp_n;while(count--){son1 *= mn1--;while(mom1!=0 && son1%mom1==0){son1 /= mom1;mom1--;}}long long son2=1;int mom2 = obstacleGrid.size()-temp_m-1;int count2 = obstacleGrid.size()-temp_m-1;int mn2 = obstacleGrid.size()-temp_m+obstacleGrid[0].size()-temp_n-2;while(count2--){son2 *= mn2--;while(mom2!=0 && son2%mom2==0){son2 /= mom2;mom2--;}}return son_sum-son1*son2;} };//
-
-
动态规划:确定dp数组(dp table)以及下标的含义,dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
-
确定递推公式:dp[i][j] = dp[i - 1] [j] + dp[i] [j - 1]。因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
-
dp数组如何初始化:从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i] [0]一定为1,dp[0] [j]也同理。但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i] [ 0]应该还是初始值0。
-
class Solution { public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m=obstacleGrid.size();int n=obstacleGrid[0].size();if(obstacleGrid[m-1][n-1]==1 || obstacleGrid[0][0]==1){return 0;}vector<vector<int>> dp(m,vector<int>(n,0));for(int i=0;i<m&&obstacleGrid[i][0]==0;i++){dp[i][0]=1;}for(int i=0;i<n&&obstacleGrid[0][i]==0;i++){dp[0][i]=1;}for(int i=1;i<m;i++){for(int j=1;j<n;j++){if(obstacleGrid[i][j]==1){continue;}dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m-1][n-1];} }; -
时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度;空间复杂度:O(n × m)
题目:整数拆分
-
给定一个正整数
n,将其拆分为k个 正整数 的和(k >= 2),并使这些整数的乘积最大化。返回 你可以获得的最大乘积 。 -
确定dp数组(dp table)以及下标的含义:dp[i]:分拆数字 i,可以得到的最大乘积为dp[i]。dp[i]的定义将贯彻整个解题过程,下面哪一步想不懂了,就想想dp[i]究竟表示的是啥!
-
确定递推公式:其实可以从1遍历j,然后有两种渠道得到dp[i].一个是j * (i - j) 直接相乘。一个是j * dp[i - j],相当于是拆分(i - j),对这个拆分不理解的话,可以回想dp数组的定义。j是从1开始遍历,拆分j的情况,在遍历j的过程中其实都计算过了。那么从1遍历j,比较(i - j) * j和dp[i - j] * j 取最大的。递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));也可以这么理解,j * (i - j) 是单纯的把整数拆分为两个数相乘,而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。所以递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
-
dp的初始化:这里我只初始化dp[2] = 1,从dp[i]的定义来说,拆分数字2,得到的最大乘积是1
-
class Solution { public:int integerBreak(int n) {vector<int> dp(n+1);dp[2]=1;for(int i=3;i<=n;i++){for(int j=1;j<=i/2;j++){dp[i]=max(dp[i],max((i-j)*j,dp[i-j]*j));}}return dp[n];} }; -
时间复杂度:O(n^2); 空间复杂度:O(n)
题目:不同的二叉搜索树
-
给你一个整数
n,求恰由n个节点组成且节点值从1到n互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 -
n为1的时候有一棵树,n为2有两棵树,来看看n为3的时候
-

- 元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
- 元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
- 元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
-
确定dp数组(dp table)以及下标的含义:dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。也可以理解是i个不同元素节点组成的二叉搜索树的个数为dp[i] ,都是一样的。
-
确定递推公式:dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量];j相当于是头结点的元素,从1遍历到i为止。所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
-
dp数组如何初始化:从定义上来讲,空节点也是一棵二叉树,也是一棵二叉搜索树,这是可以说得通的。从递归公式上来讲,dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0,也需要dp[以j为头结点左子树节点数量] = 1, 否则乘法的结果就都变成0了。
-
class Solution { public:int numTrees(int n) {vector<int> dp(n+1);dp[0]=1;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){dp[i] += dp[j-1]*dp[i-j];}}return dp[n];} }; -
时间复杂度: O ( n 2 ) O(n^2) O(n2);空间复杂度: O ( n ) O(n) O(n)
相关文章:

【C++代码】爬楼梯,不同路径,整数拆分,不同搜索树,动态规划--代码随想录
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推…...
设计模式(单例模式、工厂模式及适配器模式、装饰器模式)
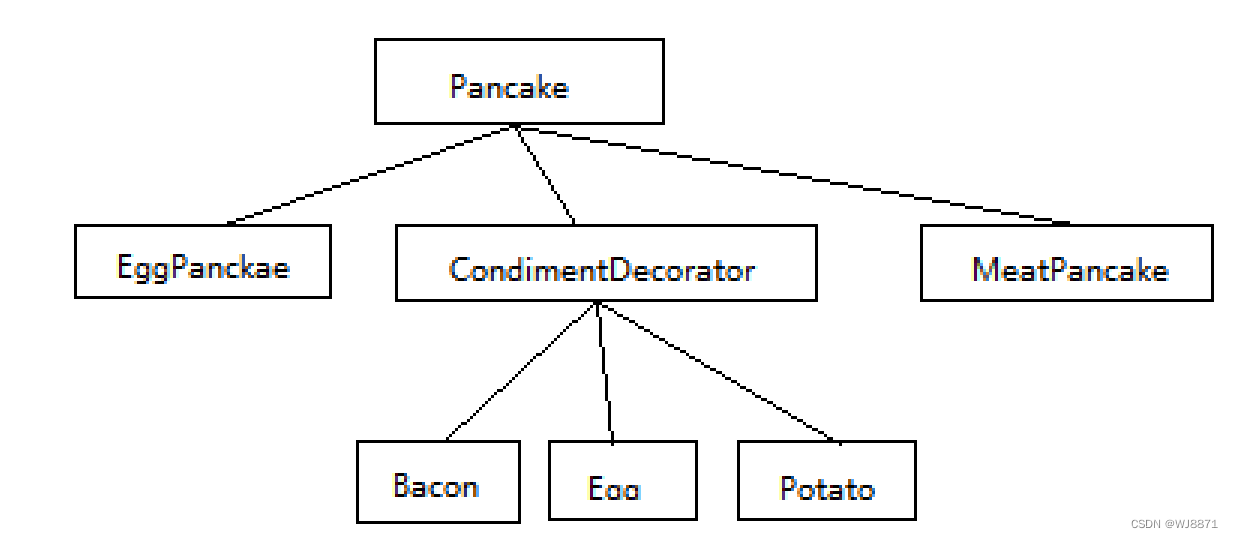
目录 0 、设计模式简介 一、单例模式 二、工厂模式 三、适配器模式 四、装饰器模式 0 、设计模式简介 设计模式可以分为以下三种: 创建型模式:用来描述 “如何创建对象”,它的主要特点是 “将对象的创建和使用分离”。包括单例、原型、工厂方法、…...

为wget命令设置代理
使用-e参数 wget本身没有专门设置代理的命令行参数,但是有一个"-e"参数,可以在命令行上指定一个原本出现在".wgetrc"中的设置。于是可以变相在命令行上指定代理: -e, --executeCOMMAND 执行.wgetrc格式的命令 例如&…...
【C++深入浅出】模版初识
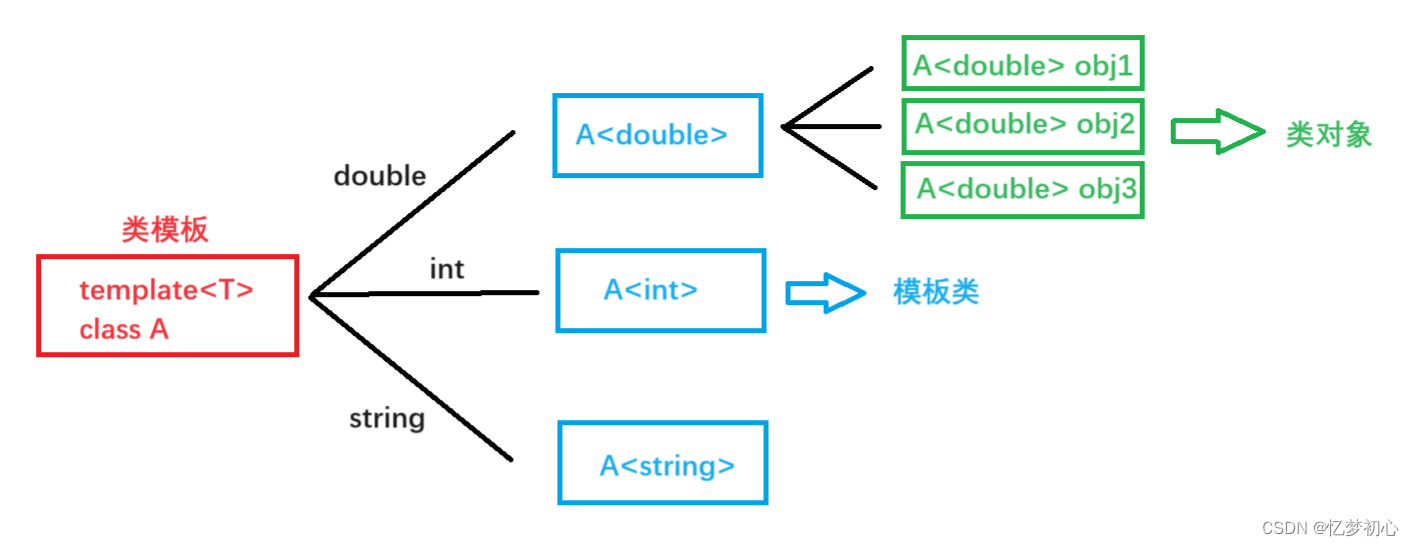
目录 一. 前言 二. 泛型编程 三. 函数模版 3.1 函数模版的概念 3.2 函数模版的格式 3.3 函数模版的原理 3.4 函数模板的实例化 3.5 模板参数的匹配原则 四. 类模版 4.1 类模版的定义 4.2 类模版的实例化 一. 前言 本期我们要介绍的是C的又一大重要功能----模版。通…...

系统架构设计师-第18章-安全架构设计理论与实践-软考学习笔记
安全架构概述 信息的可用性、元略性、机密性、可控性和不可抵赖性等安全保障显得尤为重要,而满足这些诉求,离不开好的架构设计. 信息安全面临的威胁 常见的安全威胁有以下几种. (1)信息泄露 (2) 破坏信息的元整性: 数据被非授极地进行增删、修改成破坏…...

2023年吉安市“振兴杯”职业技能大赛网络安全项目样题
2023年吉安市“振兴杯”职业技能大赛 网络安全项目样题 需要竞赛环境可私信博主 赛题说明 一、竞赛项目简介 竞赛共分为:A.基础设施设置与安全加固;B.网络安全事件响应、数字取证调查和应用安全;C.CTF夺旗-攻击;D.CTF夺旗-防御等四…...

python爬虫selenium和ddddocr使用
python爬虫selenium和ddddocr使用 selenium使用 selenium实际上是web自动化测试工具,能够通过代码完全模拟人使用浏览器自动访问目标站点并操作来进行web测试。 通过pythonselenium结合来实现爬虫十分巧妙。 由于是模拟人的点击来操作,所以实际上被反…...

【vim 学习系列文章 12 -- vimrc 那点事】
文章目录 系统级及本地 vimrc 文件设置 vimrc 的路径 系统级及本地 vimrc 文件 当 Vim 启动时,编辑器会去搜索一个系统级的 vimrc 文件来进行系统范围内的默认初始化工作。 这个文件通常在你系统里 $VIM/vimrc 的路径下,如果没在那里,那你可…...

spring.factories介绍
spring.factories 是 Spring Framework 中的一个配置文件,它用于自动装配和加载 Spring 应用程序中的各种组件。该文件位于 META-INF/spring.factories,通常位于 JAR 文件的资源路径下。 spring.factories 文件采用键值对的形式,每个键代表一…...
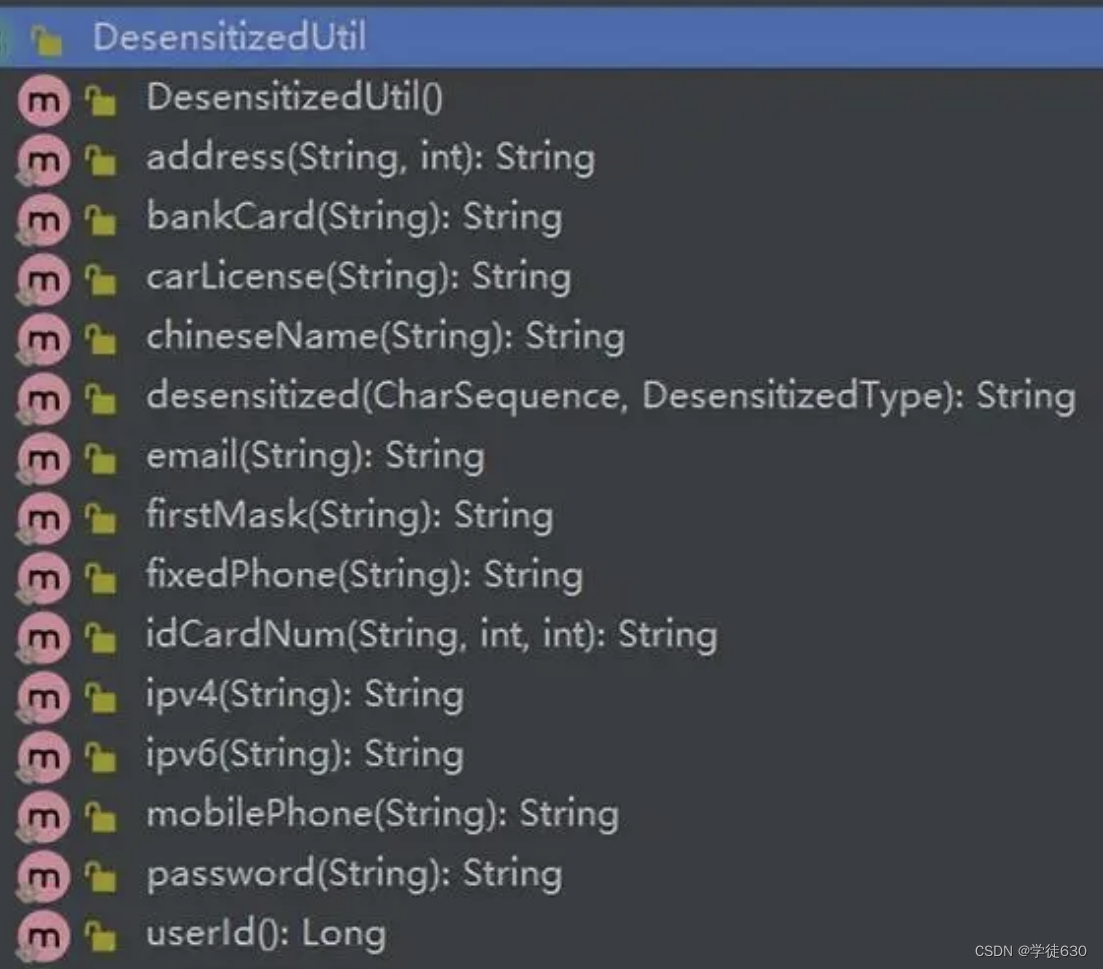
业务设计——用户敏感信息展示脱敏及其反脱敏
业务需求 将用户敏感信息脱敏展示到前端是出于保护用户隐私和信息安全的考虑。 敏感信息包括但不限于手机号码、身份证号、银行卡号等,这些信息泄露可能导致用户个人信息的滥用、身份盗用等严重问题。脱敏是一种常用的保护用户隐私的方式,它的目的是减少…...

Hadoop分布式安装
首先准备好三台服务器或者虚拟机,我本机安装了三个虚拟机,安装虚拟机的步骤参考我之前的一篇 virtualBox虚拟机安装多个主机访问虚拟机虚拟机访问外网配置-CSDN博客 jdk安装 参考文档:Linux 环境下安装JDK1.8并配置环境变量_linux安装jdk1.8并…...

Python——PyQt5以及Pycharm相关配置
PyQt5目录 常见的GUI框架一、安装pyqt5pip install pyqt5pip install pyqt5-tools二、Qt Designer三、在PyCharm中配置相关toolQtDisigner配置PyUIC配置PyRCC配置常见的GUI框架 Tkinter:Python内置的GUI框架,使用TCL实现,Python中内嵌了TCL解释器,使用它的时候不用安装额外…...

java集成海康预览抓图出现内存一直上涨问题
求助:在java 中集成海康sdk后批量抓图出现内存上涨问题,不论是预览后不关闭继续预览,还是预览后关闭预览,然后重新预览都没有解决这个问题(抓图正常),尝试使用第三方解码器ffmpeg来进行解码&…...
Spring Boot 使用 Disruptor 做内部高性能消息队列
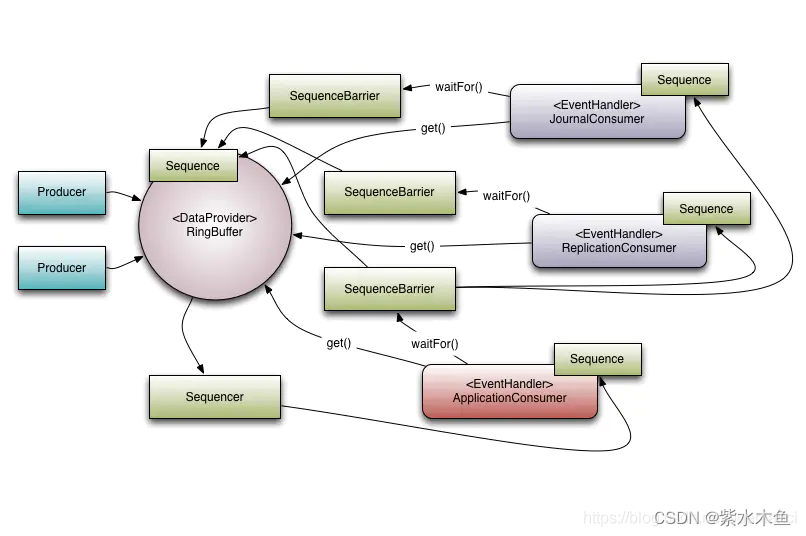
这里写自定义目录标题 一 、背景二 、Disruptor介绍三 、Disruptor 的核心概念3.1 Ring Buffer3.2 Sequence Disruptor3.3 Sequencer3.4 Sequence Barrier3.5 Wait Strategy3.6 Event3.7 EventProcessor3.8 EventHandler3.9 Producer 四、案例-demo五、总结 一 、背景 工作中遇…...
一、灵动mm32单片机_开发环境的搭建(Keil)
1、安装Keil MDK。 略。 2、安装芯片对应的Pack包。 (1)这里以MM32F0130单片机为例。 (2)进入灵动微电子官网。上海灵动微电子股份有限公司 (3)点击“支持”→“KEILPacl”。 (3)点击下载Pack包。 (4)下载后,解压下载的压缩包,找到对应的Pack包&…...

【5G PHY】5G SS/PBCH块介绍(二)
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

简单而高效:使用PHP爬虫从网易音乐获取音频的方法
概述 网易音乐是一个流行的在线音乐平台,提供了海量的音乐资源和服务。如果你想从网易音乐下载音频文件,你可能会遇到一些困难,因为网易音乐对其音频资源进行了加密和防盗链的处理。本文将介绍一种使用PHP爬虫从网易音乐获取音频的方法&…...

渗透测试工具-sqlmap使用
sqlmap是一个开源渗透测试的自动化工具,可以自动检测和利用SQL注入漏洞并接管数据库服务器。它配备了一个强大的检测引擎,许多用于终极渗透测试的利基功能,以及广泛的开关,包括数据库指纹识别、从数据库中获取数据、访问底层文件系…...

C# WPF: Imag图片填充方式有哪些?
C#和WPF中的图像填充方式 在WPF中,你可以使用Image控件来显示图像,并使用不同的填充方式来控制图像在控件中的显示方式。以下是一些常见的图像填充方式: Stretch(拉伸):这是默认的填充方式,它…...

uniapp开发小程序—根据生日日期计算年龄 周岁
0、需求 在UniApp开发小程序中,将接口返回的出生日期转化为年龄;判断接口返回的年龄是否是周岁 可以使用JavaScript的日期处理方法来实现。 一、第一种方式(示例代码): //javascript // 假设接口返回的年龄为生日的…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
