代码随想录算法训练营第三十八天丨 动态规划part01
动态规划理论基础
动态规划刷题大纲
什么是动态规划
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的,
在关于贪心算法,你该了解这些! (opens new window)中卡哥举了一个背包问题的例子。
例如:有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
动态规划中 dp[j] 是由 dp[j-weight[i]] 推导出来的,然后取max(dp[j], dp[j - weight[i]] + value[i])。
但如果是贪心呢,每次拿物品选一个最大的或者最小的就完事了,和上一个状态没有关系。
所以贪心解决不了动态规划的问题。
不用死扣动规和贪心的理论区别,慢慢的就知道了
动规是由前一个状态推导出来的,而贪心是局部直接选最优的
动态规划的解题步骤
状态转移公式(递推公式)是很重要,但动规不仅仅只有递推公式。
对于动态规划问题,卡哥将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
为什么要先确定递推公式,然后在考虑初始化呢?
因为一些情况是递推公式决定了dp数组要如何初始化!
动态规划应该如何debug
找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!
做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果。
然后再写代码,如果代码没通过就打印dp数组,看看是不是和自己预先推导的哪里不一样。
如果打印出来和自己预先模拟推导是一样的,那么就是自己的递归公式、初始化或者遍历顺序有问题了。
如果和自己预先模拟推导的不一样,那么就是代码实现细节有问题。
这样才是一个完整的思考过程,而不是一旦代码出问题,就毫无头绪的东改改西改改,最后过不了,或者说是稀里糊涂的过了。
这也是卡哥为什么在动规五步曲里强调推导dp数组的重要性。
举个例子哈:在「代码随想录」刷题小分队微信群里,一些录友可能代码通过不了,会把代码抛到讨论群里问:我这里代码都已经和题解一模一样了,为什么通过不了呢?
发出这样的问题之前,其实可以自己先思考这三个问题:
- 这道题目我举例推导状态转移公式了么?
- 我打印dp数组的日志了么?
- 打印出来了dp数组和我想的一样么?
如果这灵魂三问自己都做到了,基本上这道题目也就解决了,或者更清晰的知道自己究竟是哪一点不明白,是状态转移不明白,还是实现代码不知道该怎么写,还是不理解遍历dp数组的顺序。
然后在问问题,目的性就很强了,群里的小伙伴也可以快速知道提问者的疑惑了。
注意这里不是说不让大家问问题哈, 而是说问问题之前要有自己的思考,问题要问到点子上!
我们工作之后就会发现,特别是大厂,问问题是一个专业活,是的,问问题也要体现出专业!
如果问同事很不专业的问题,同事们会懒的回答,领导也会认为你缺乏思考能力,这对职场发展是很不利的。
所以大家在刷题的时候,就锻炼自己养成专业提问的好习惯。
今天开始新的征程了,加油!!!
509. 斐波那契数
思路
动态规划
动规五部曲:
这里我们要用一个一维dp数组来保存递归的结果
- 1、确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
- 2、确定递推公式
为什么这是一道非常简单的入门题目呢?
因为题目已经把递推公式直接给我们了:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
- 3、dp数组如何初始化
题目中把如何初始化也直接给我们了,如下:
dp[0] = 0;
dp[1] = 1;
- 4、确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
- 5、举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。
代码如下:
class Solution {public int fib(int n) {if(n == 0 || n ==1){return n;}//1.确定dp数组下标含义//2.确定递推公式 dp[i] = dp[i-1] + dp[i-2];//3.dp数组初始化int[] dp = new int[n+1];dp[0] = 0;dp[1] = 1;//4.确定遍历顺序:从前往后for(int i = 2;i <= n;i++){dp[i]=dp[i-1]+dp[i-2];}//5.举例推导dp数组return dp[n];}
}70. 爬楼梯
思路
举几个例子,就可以发现其规律。
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
我们来分析一下,动规五部曲:
定义一个一维数组来记录不同楼层的状态
- 1/确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法
- 2/确定递推公式
如何可以推出dp[i]呢?
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。
在推导dp[i]的时候,一定要时刻想着dp[i]的定义,否则容易跑偏。
这体现出确定dp数组以及下标的含义的重要性!
- 3、dp数组如何初始化
再回顾一下dp[i]的定义:爬到第i层楼梯,有dp[i]种方法。
那么i为0,dp[i]应该是多少呢,这个可以有很多解释,但基本都是直接奔着答案去解释的。
例如强行安慰自己爬到第0层,也有一种方法,什么都不做也就是一种方法即:dp[0] = 1,相当于直接站在楼顶。
但总有点牵强的成分。
那还这么理解呢:卡哥就认为跑到第0层,方法就是0啊,一步只能走一个台阶或者两个台阶,然而楼层是0,直接站楼顶上了,就是不用方法,dp[0]就应该是0.
其实这么争论下去没有意义,大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过,然后就往结果上靠去解释dp[0] = 1。
从dp数组定义的角度上来说,dp[0] = 0 也能说得通。
需要注意的是:题目中说了n是一个正整数,题目根本就没说n有为0的情况。
所以本题其实就不应该讨论dp[0]的初始化!
我相信dp[1] = 1,dp[2] = 2,这个初始化大家应该都没有争议的。
所以卡哥的原则是:不考虑dp[0]如何初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推,这样才符合dp[i]的定义。
- 4、确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的
- 5、举例推导dp数组
举例当n为5的时候,dp table(dp数组)应该是这样的
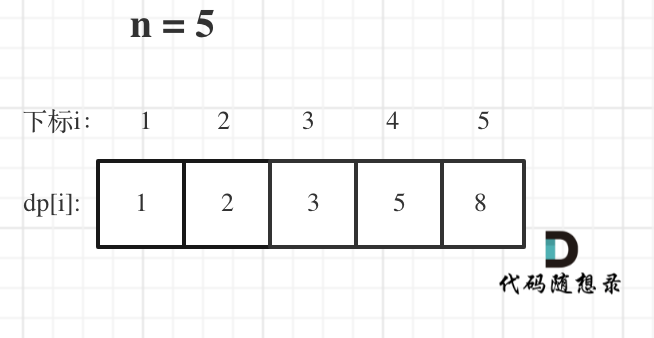
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
此时发现了,这不就是斐波那契数列么!
唯一的区别是,没有讨论dp[0]应该是什么,因为dp[0]在本题没有意义!
代码如下:
class Solution {public int climbStairs(int n) {if(n == 1 || n==2){return n;}int[] dp = new int[n+1];dp[1]=1;dp[2]=2;for(int i =3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];}return dp[n];}
}746. 使用最小花费爬楼梯
思路
修改之后的题意就比较明确了,题目中说 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯” 也就是相当于 跳到 下标 0 或者 下标 1 是不花费体力的, 从 下标 0 下标1 开始跳就要花费体力了。
- 1、确定dp数组以及下标的含义
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
对于dp数组的定义,一定要清晰!
- 2、确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
- 3、dp数组如何初始化
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
那么 dp[0] 应该是多少呢? 根据dp数组的定义,到达第0台阶所花费的最小体力为dp[0],那么有同学可能想,那dp[0] 应该是 cost[0],例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话,dp[0] 就是 cost[0] 应该是1。
这里就要说明本题力扣为什么改题意,而且修改题意之后 就清晰很多的原因了。
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
- 4、确定遍历顺序
最后一步,递归公式有了,初始化有了,如何遍历呢?
本题的遍历顺序其实比较简单,简单到很多同学都忽略了思考这一步直接就把代码写出来了。
因为是模拟台阶,而且 dp[i]由dp[i-1]dp[i-2] 推出,所以是从前到后遍历cost数组就可以了。
但是稍稍有点难度的动态规划,其遍历顺序并不容易确定下来。 例如:01背包,都知道两个for循环,一个for遍历物品嵌套一个for遍历背包容量,那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢? 以及在使用一维dp数组的时候遍历背包容量为什么要倒序呢?
这些都与遍历顺序息息相关。当然背包问题后续「代码随想录」都会重点讲解的!
- 5、举例推导dp数组
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
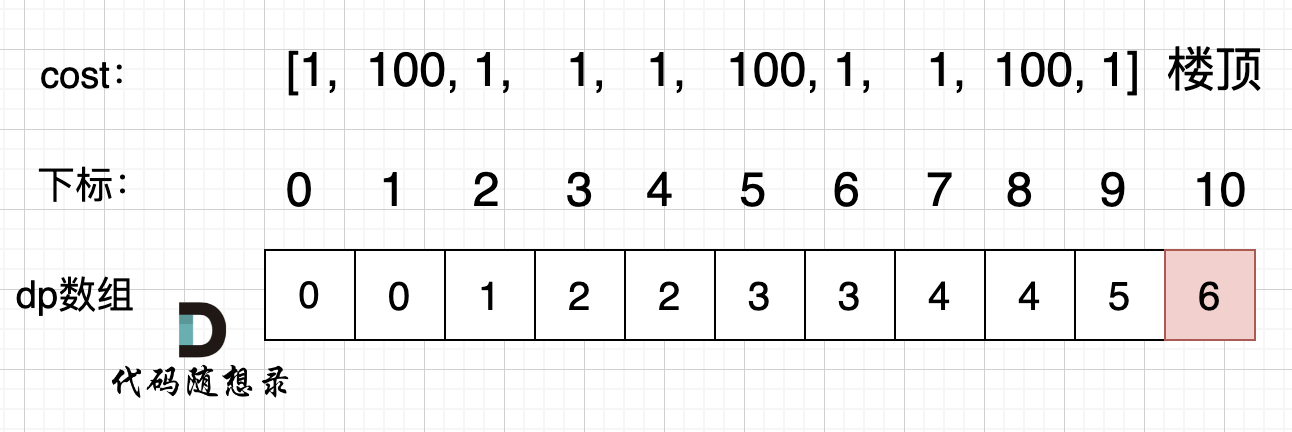
如果代码写出来有问题,就把dp数组打印出来,看看和如上推导的是不是一样的。
代码如下:
class Solution {public int minCostClimbingStairs(int[] cost) {int[] dp = new int[cost.length+1];dp[0] = 0;dp[1] = 0;for (int i = 2; i <= cost.length; i++) {dp[i] = Math.min(dp[i-1] +cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.length];}
}第一次接触动态规划,对于一些概念和逻辑不清晰,但经过第一天的引导之后整体对dp有了一个整体的认识。
相关文章:

代码随想录算法训练营第三十八天丨 动态规划part01
动态规划理论基础 动态规划刷题大纲 什么是动态规划 动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。 所以动态规划中每一个状态一定是由上一个状态推导出来的&a…...
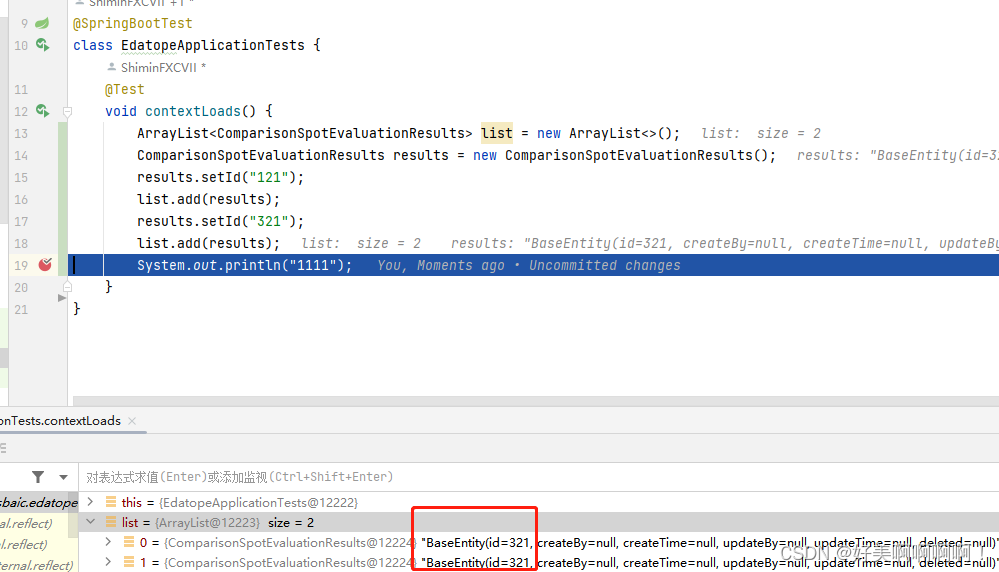
关于集合遇到的坑
public void invoke(ComparisonSpotEvaluationResultsExcel comparisonSpotEvaluationResultsExcel, AnalysisContext analysisContext) {/*** 记录行号码*/ReadRowHolder readRowHolder analysisContext.readRowHolder();Integer rowIndex readRowHolder.getRowIndex();Stri…...

需要下微信视频号视频的小伙伴们看过来~
随着视频号的热度越来越大,下载视频号视频的需求也开始增加啦,今天给大家给分享几个简单实用的下载方法,总有一个你能用上的! 一、犀牛视频下载 犀牛视频下载器可以直接解析并下载视频号短视频。您只需转发视频到机器人即可下载。…...

测试工具:hurl
文章目录 Hurlinstallstartdemo 功能使用变量Capturing values 捕获值Asserts 断言生成报告 Hurl 官网:https://hurl.dev/ Hurl 是一个命令行工具,它运行以简单的纯文本格式定义的 HTTP 请求。 它可以发送请求、捕获值并评估对标头和正文响应的查询 i…...

RateLimiter限流
使用场景 限流是高并发的处理方法之一。 高并发处理方案: 缓存:缓存的目的是提升系统访问速度和增大系统处理容量。 降级:降级是当服务出现问题或者影响到核心流程时,需要暂时屏蔽掉,待高峰或者问题解决后再打开。…...
PMP适合哪些人去考?
许多人都在考虑是否适合考取PMP证书,我来解答你的疑惑:无论是IT、建筑、制药、制造业、电信、金融还是通信领域,PMP证书都得到广泛认可。虽然IT行业目前占比最大,但近几年T业比重下降,制造业、金融、能源和建筑工程等的…...

钡铼技术 工控机中的X86和ARM处理器:哪个更具可扩展性?
X86和ARM是两种不同的处理器架构,它们在工控机中的应用也有所不同。 X86架构的处理器是英特尔公司和AMD公司生产的,它们主要应用于个人电脑和服务器等领域。X86架构的处理器具有良好的通用性和兼容性,可以运行各种操作系统和应用软件。X86架…...
)
软考 系统架构设计师系列知识点之软件构件(3)
接前一篇文章:软考 系统架构设计师系列知识点之软件构件(2) 所属章节: 第2章. 计算机系统基础知识 第3节. 计算机软件 2.3.7 软件构件 (2)J2EE(补充知识) J2EE核心组成:…...

中科驭数亮相2023中国移动全球合作伙伴大会
10月11-13日,2023中国移动全球合作伙伴大会开幕。中科驭数作为移动云COCA生态合作伙伴,受邀出席“算网融百业数智赢未来”政企分论坛,高级副总裁张宇上台参与移动云OpenCOCA开源项目和《OpenCOCA白皮书》的重磅发布仪式,助力构建未…...
研发流程一:数据库的调研与介绍)
WebGIS国产化(信创)研发流程一:数据库的调研与介绍
眼下互联网产业国产化已经成为不可阻挡的趋势,WebGIS的开发工作也不例外,越来越依靠纯国产的软件和产品,甚至是框架。企业中使用国产软件和产品的项目占比也在不断升高,我将分享一系列的文章给大家,来共同研究GIS的国产…...

[Shell] ${} 的多种用法
文章目录 解释代码 解释 在Shell脚本中,${} 是一种变量替换语法。它用于获取和操作变量的值。 具体来说,${} 可以用来执行以下操作: 变量引用:${variable} 表示引用变量 variable 的值。 变量默认值:${variable:-de…...
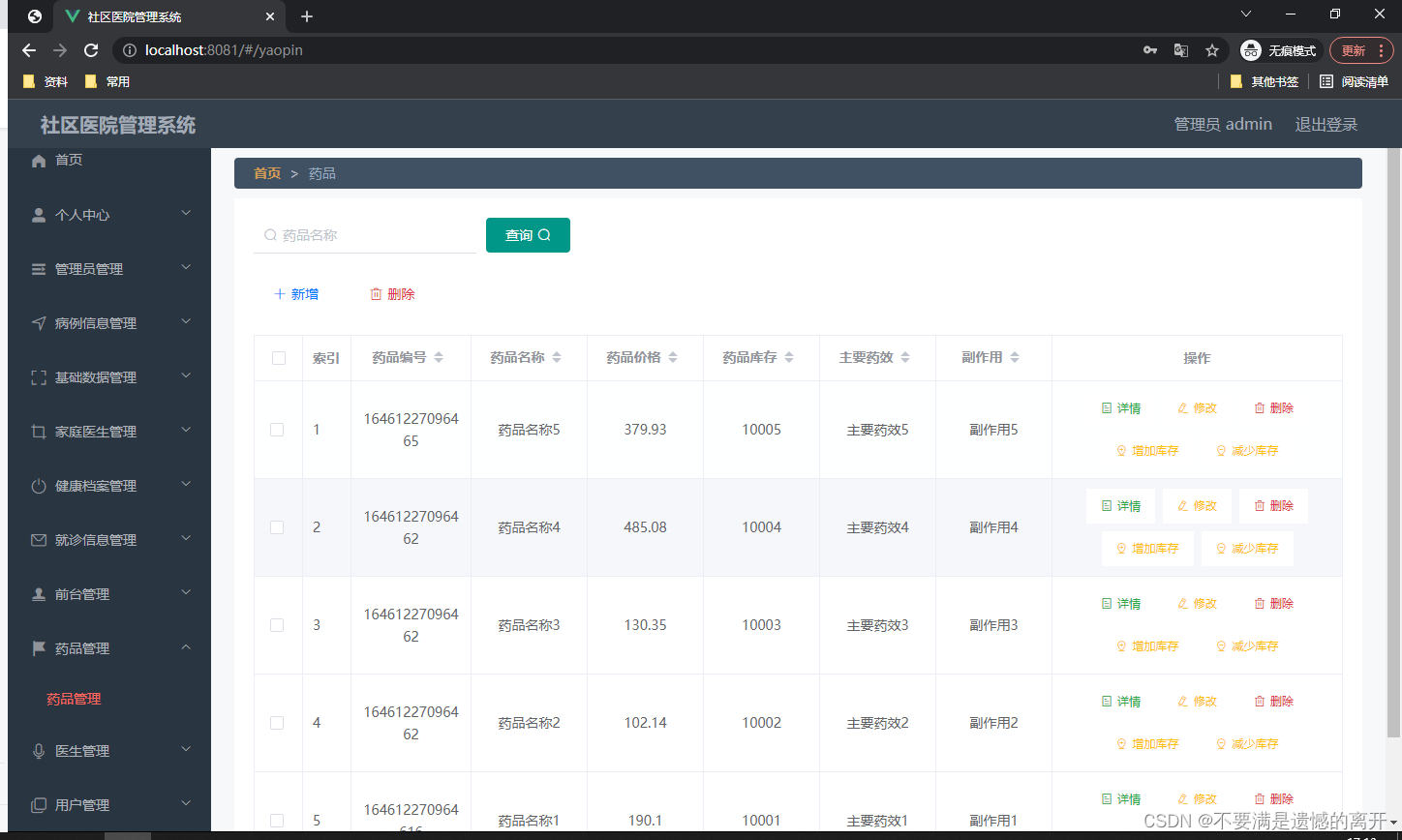
基于SpringBoot的社区医院管理系统设计与实现
目录 前言 一、技术栈 二、系统功能介绍 管理员功能实现 用户信息管理 病例信息管理 家庭医生管理 药品信息管理 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 信息数据从传统到当代,是一直在变革当中,突如其来的互联网让传统的…...
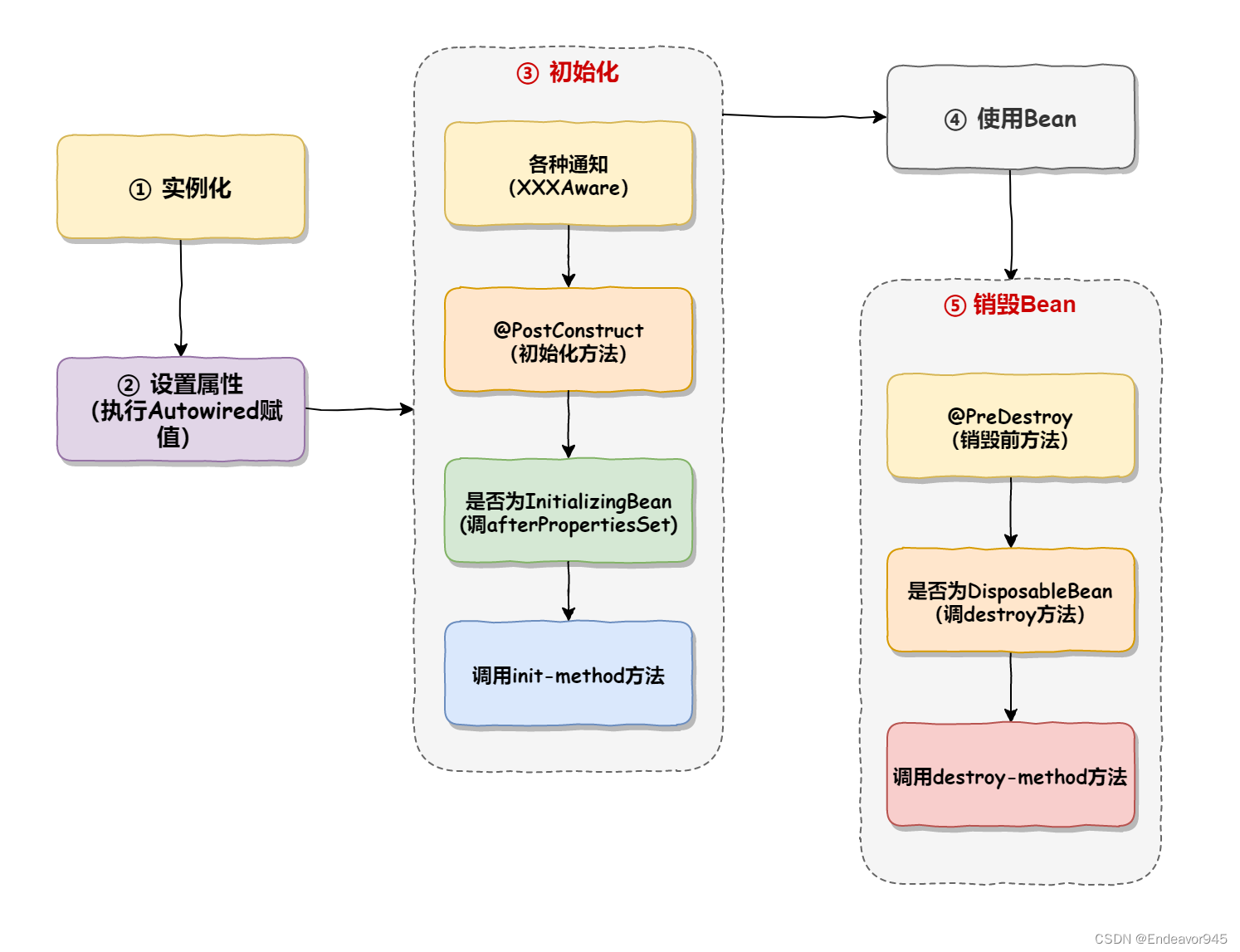
Spring的执行流程与Bean的生命周期
目录 一、Spring的执行流程(生命周期) 二、Bean的生命周期 一、Spring的执行流程(生命周期) 首先在Spring的执行过程中会先启动容器,这里是将配置文件进行加载。根据配置文件完成Bean的实例化,比如是配置的…...
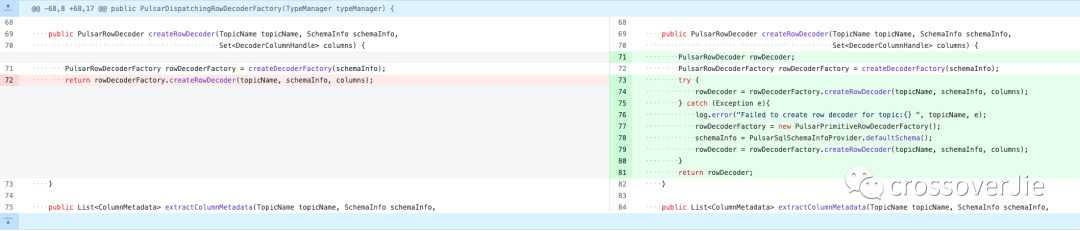
使用 SQL 的方式查询消息队列数据以及踩坑指南
背景 为了让业务团队可以更好的跟踪自己消息的生产和消费状态,需要一个类似于表格视图的消息列表,用户可以直观的看到发送的消息;同时点击详情后也能查到消息的整个轨迹。 消息列表 点击详情后查看轨迹 原理介绍 由于 Pulsar 并没有关系型数…...

拿下国家级信创认证 中科驭数KPU SWIFT-2200N成为国内首款满足金融业严苛要求的DPU产品
近日,中科驭数KPU SWIFT-2200N低时延DPU卡,在中国人民银行旗下金融信创生态实验室完成测试并取得测试报告,这意味着中科驭数低时延网络代表性产品的应用领域从证券进一步拓展到了银行业,成为国内首款满足金融行业严苛要求的DPU产品…...

centos怎么禁用和关闭selinux
要禁用和关闭SELinux(Security-Enhanced Linux)在CentOS上,请按照以下步骤进行: 请注意:禁用SELinux会减少系统的安全性,因此只有在确切知道自己在做什么并且出于特定目的时才应该这样做。 1.打开终端并以超级用户(root)身份登录&…...

【LeetCode刷题日志】88.合并两个有序数组
🎈个人主页:库库的里昂 🎐C/C领域新星创作者 🎉欢迎 👍点赞✍评论⭐收藏✨收录专栏:LeetCode 刷题日志🤝希望作者的文章能对你有所帮助,有不足的地方请在评论区留言指正,…...

计算机考研 | 2013年 | 计算机组成原理真题
文章目录 【计算机组成原理2013年真题43题-9分】【第一步:信息提取】【第二步:具体解答】 【计算机组成原理2013年真题44题-14分】【第一步:信息提取】【第二步:具体解答】 【计算机组成原理2013年真题43题-9分】 某32位计算机&a…...
[Unity][VR]透视开发系列4-解决只看得到Passthrough但看不到Unity对象的问题
【视频资源】 视频讲解地址请关注我的B站。 专栏后期会有一些不公开的高阶实战内容或是更细节的指导内容。 B站地址: https://www.bilibili.com/video/BV1Zg4y1w7fZ/ 我还有一些免费和收费课程在网易云课堂(大徐VR课堂): https://study.163.com/provider/480000002282025/…...

电气工程 自动化 机械工科学生来看看
PLC 类 基于PLC的机械手控制系统设计 基于PLC的机械手控制系统设计 PLC与变频器在综采设备上的应用 PLC与步进电机的运动控制编程9000 PLC应用数字电子钟设计 三菱FX系列PLC与三菱变频器通讯应用实例 基于plc拉杆箱振动与噪音检测平台设计 基于PLC的船舶空压机控制系统设计 基…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
