隐私计算python实现Paillier同态加密
1.基本概念
Paillier同态加密是一种公钥加密方案,具有同态加密的特性。它由Pascal Paillier于1999年提出。
Paillier同态加密基于数论问题,其安全性基于大整数分解问题和离散对数问题的困难性。该方案可以用于保护隐私数据,同时支持在加密状态下对加密的数据进行运算。
Paillier同态加密方案包含两个主要算法:加密算法和解密算法。其中,加密算法用于将明文加密为密文,解密算法用于将密文解密为明文。此外,该方案还包括一个密钥生成算法,用于生成加密和解密所需的公钥和私钥。
2.加解密过程
2.1密钥生成
1.随机选择两个长度相等的大素数p,q,并满足gcd(pq,(p-1)(q-1))=1,这里gcd表示最大公约数。
2.计算n=pq以及λ=lcm(p-1,q-1),这里lcm表示最小公倍数
3.随机选择整数g(也可以令g=n+1)
4.定义L函数:L(x)=(x-1)/n,计算
公钥pk=(n,g),私钥sk=(λ,μ)
2.2加密
1.输入明文信息m
2.选择随机整数r,且gcd(r,n)=1
3.计算密文
2.3解密
1.输入密文c
2.计算明文
2.4同态加证明
3.加解密示例
3.1密钥生成
1.这里我们p、q选取简单的素数,即p=17,q=23
2.计算n=pq=391,λ=lcm(16,22)=176
3.取整数g=n+1=392
4.计算
公钥pk=(n,g)=(391,392),私钥sk=(176,20)
3.2加密
1.明文m=8
2.选择随机数r=5,gcd(5,391)=1
3.计算密文
3.3解密
1.输入密文15310
2.计算明文
4.代码实现
"""
@Time : 2023/10/8 0008 16:17
@Auth : yeqc
"""
# 部分同态加密: paillier同态加密from phe import paillier# 创建Paillier 密钥对
public_key, private_key = paillier.generate_paillier_keypair()# # 明文
# M = 42
# # 加密明文
# encrypted_M = public_key.encrypt(M)
#
# # 解密密文
# decrypted_M = private_key.decrypt(encrypted_M)
#
# print(f'明文{M}')
# print(f'加密密文:{encrypted_M.ciphertext()}')#.ciphertext()实现纯文本输出
# print(f'解密密文:{decrypted_M}')# ------------------以下是密文加 实现明文加-------------------
# 明文
M1, M2 = 25, 70
# 加密密文
encrypted_M1, encrypted_M2 = public_key.encrypt(M1), public_key.encrypt(M2)# 密文相加
en_M_sum = encrypted_M1 + encrypted_M2
# 解密密文
de_M_sum = private_key.decrypt(en_M_sum)
print(f'M1 = {M1},M2 = {M2}')
print(f'M1加密密文 en_M1 = {encrypted_M1}, M2加密密文 en_M2 = {encrypted_M2}')
print(f'密文相加 en_M_sum = {en_M_sum}')
print(f'解密密文 de_M_sum = {de_M_sum}')相关文章:
隐私计算python实现Paillier同态加密
1.基本概念 Paillier同态加密是一种公钥加密方案,具有同态加密的特性。它由Pascal Paillier于1999年提出。 Paillier同态加密基于数论问题,其安全性基于大整数分解问题和离散对数问题的困难性。该方案可以用于保护隐私数据,同时支持在加密状态…...

代码随想录打卡第五十五天|● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
300.最长递增子序列 **题目:**给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0…...

C# 创建Oceanbase ODBC数据源 DSN
需要管理员权限打开VS,因为只有管理员权限可以修改注册表 using Microsoft.Win32; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Data.Odbc; using System.Diagnostics; using System.Drawing;…...
)
C++ 常用函数汇总#include<algorithm>(3万字总结)
文章目录 1. 排序(Sorting)1.1 sort(first, last):对指定范围内的元素进行升序排序1.2 stable_sort(first, last):在保持相等元素的相对顺序的情况下对指定范围内的元素进行排序1.3 partial_sort(first, middle, last):对范围内的元素进行部分排序,使得前部分是最小的,但…...

Google Archive Patch 基础应用代码记录
项目地址 Google Archive Patch 前置 <!-- 差量应用模块 --> <dependency><groupId>com.google.archivepatcher</groupId><artifactId>archive-patch-applier</artifactId><version>1.0.4</version><scope>test</…...
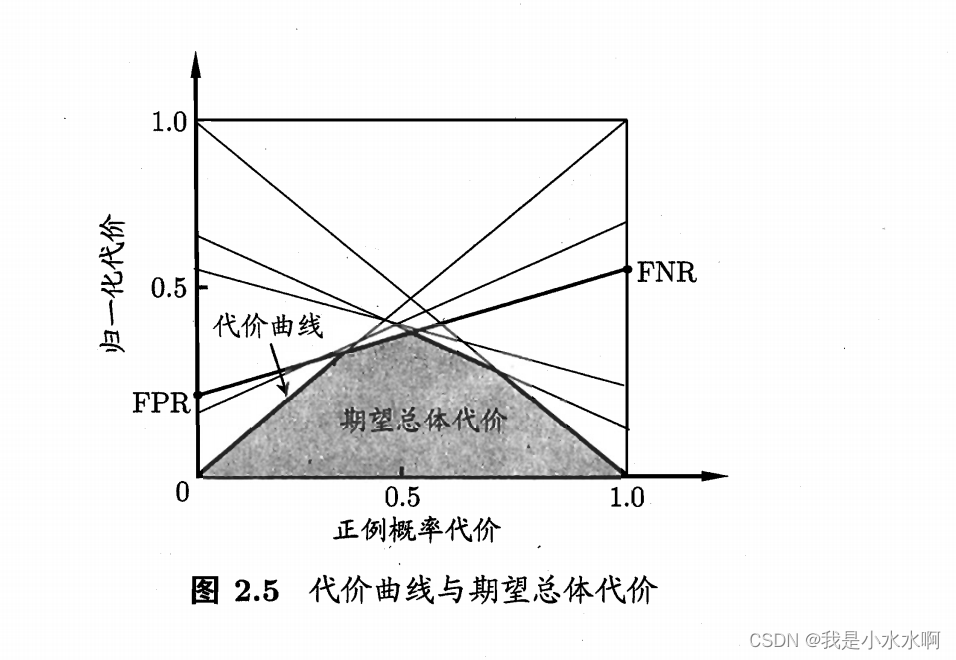
机器学习——代价敏感错误率与代价曲线
文章目录 代价敏感错误率实现代价曲线例子 代价敏感错误率 指在分类问题中,不同类别的错误分类所造成的代价不同。在某些应用场景下,不同类别的错误分类可能会产生不同的代价。例如,在医学诊断中,将疾病患者错误地分类为健康人可…...

如何利用 ChatGPT 提升编程技能
目录 前言代码命名与 ChatGPT设计模式与 ChatGPT代码重构与 ChatGPT代码优化与 ChatGPTChatGPT 的潜在挑战与限制成功案例分析最佳实践与注意事项结语 前言 编程是一项充满创造性和挑战的任务,但也是一个需要花费大量时间和精力的领域。在日益复杂的软件开发环境中…...
是什么意思)
ChatGPT:@EqualsAndHashCode(callSuper = false)是什么意思
ChatGPT:EqualsAndHashCode(callSuper false)是什么意思 EqualsAndHashCode(callSuper false)是什么意思? ChatGPT: EqualsAndHashCode(callSuper false) 是 Java 中的 Lombok 注解,用于自动生成 equals() 和 hashCode() 方法…...

docker部署的mariadb忘记密码
docker 里的 mariadb 数据库密码忘了,如果以前我会选择直接干掉重装,但是数据怎么办? 1 数据量小 就跳过密码登录进去备份出来 2 想办法改掉密码 我直接选择后者,跳过密码,mariadb10.4以后不能直接改密码了ÿ…...
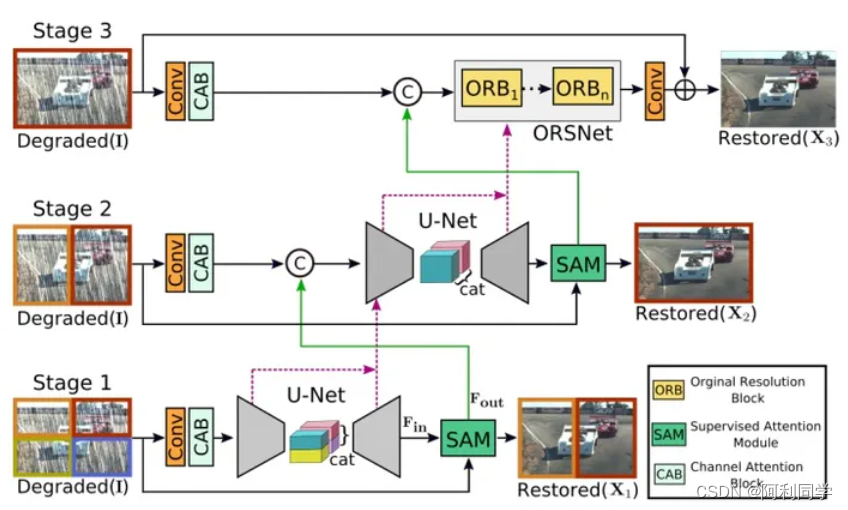
一体化模型图像去雨+图像去噪+图像去模糊(图像处理-图像复原-代码+部署运行教程)
本文主要讲述了一体化模型进行去噪、去雨、去模糊,也就是说,一个模型就可以完成上述三个任务。实现了良好的图像复原功能! 先来看一下美女复原.jpg 具体的: 在图像恢复任务中,需要在恢复图像的过程中保持空间细节…...
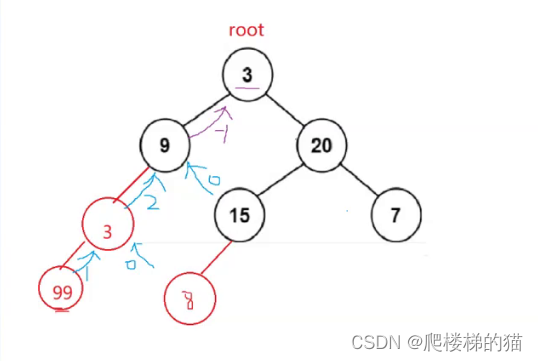
[java/力扣110]平衡二叉树——优化前后的两种方法
分析 根据平衡二叉树的定义,只需要满足:1、根节点两个子树的高度差不超过1;2、左右子树都为平衡二叉树 代码 public class BalancedBinaryTree {public class TreeNode{int val;TreeNode left;TreeNode right;TreeNode(){}TreeNode(int va…...
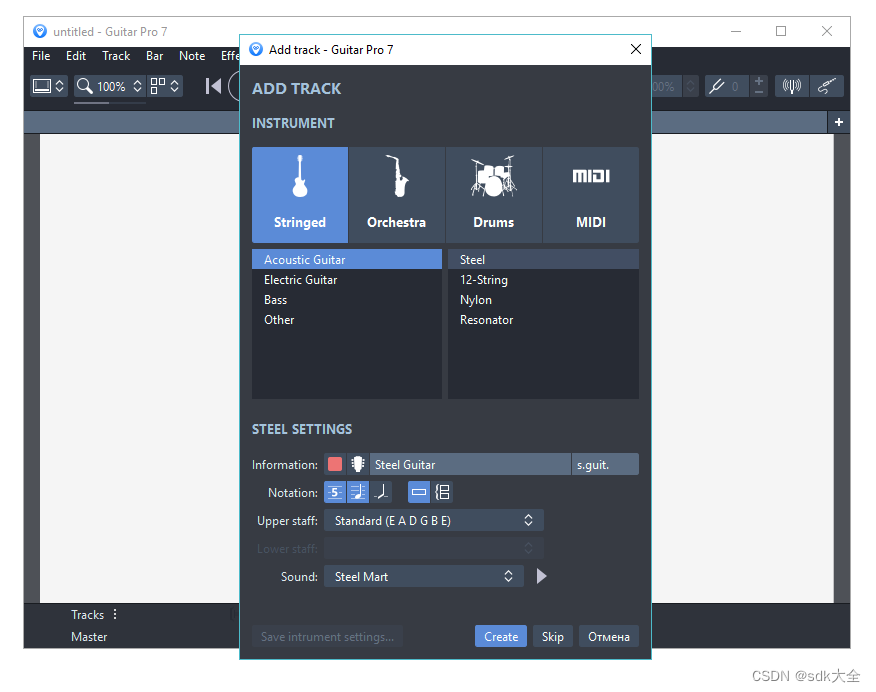
吉他、班卓琴和贝斯吉他降分器:Arobas Music Guitar 8.1.1
Arobas Music Guitar 是一款专业的吉他、班卓琴和贝斯吉他降分器。在熟练的手中,它不仅可以让您创作,还可以编辑、聆听和录制,以及导入和导出乐谱。如果有人感兴趣的话,录音是在八个轨道上进行的,你可以为每个轨道单独…...
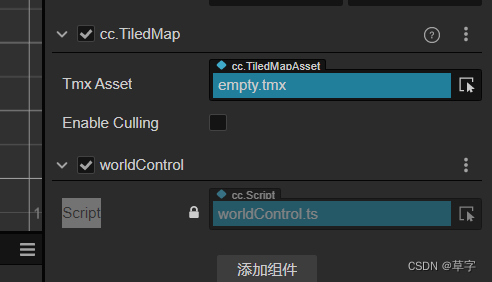
cocos tilemap的setTileGIDAt方法不实时更新
需要取消勾选 Enable Culling。同时代码添加:markForUpdateRenderData函数。 floor.setTileGIDAt(102427,newP.x,newP.y,0); //中心 floor.markForUpdateRenderData(); 具体问题参考官网说明: Cocos Creator 3.2 手册 - 项目设置...

机器学习---使用 TensorFlow 构建神经网络模型预测波士顿房价和鸢尾花数据集分类
1. 预测波士顿房价 1.1 导包 from __future__ import absolute_import from __future__ import division from __future__ import print_functionimport itertoolsimport pandas as pd import tensorflow as tftf.logging.set_verbosity(tf.logging.INFO) 最后一行设置了Ten…...

铁合金电炉功率因数补偿装置设计
摘要 由于国内人民生活水平的提高,科技不断地进步,控制不断地完善,从而促使功率因数补偿装置在电力等系统领域占据主导权,也使得功率因数补偿控制系统被广泛应用。在铁合金电炉系统设计领域中,功率因数补偿控制成为目前…...

表格识别软件:科技革新引领行业先锋,颠覆性发展前景广阔
表格识别软件的兴起背景可以追溯到数字化和自动化处理的需求不断增加的时期。传统上,手动处理纸质表格是一项费时费力的工作,容易出现错误,效率低下。因此,开发出能够自动识别和提取表格数据的软件工具变得非常重要。 随着计算机…...
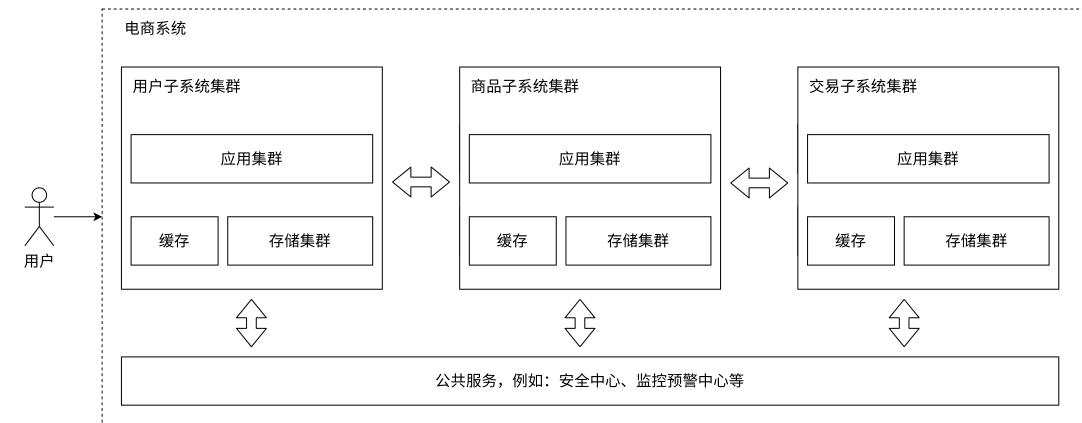
【Redis】高并发分布式结构服务器
文章目录 服务端高并发分布式结构名词基本概念评价指标1.单机架构缺点 2.应用数据分离架构应用服务集群架构读写分离/主从分离架构引入缓存-冷热分离架构分库分表(垂直分库)业务拆分⸺微服务 总结 服务端高并发分布式结构 名词基本概念 应⽤࿰…...

微信小程序拍照页面自定义demo
api文档 <template><div><imagemode"widthFix"style"width: 100%; height: 300px":src"imageSrc"v-if"imageSrc"></image><camerav-else:device-position"devicePosition":flash"flash&qu…...
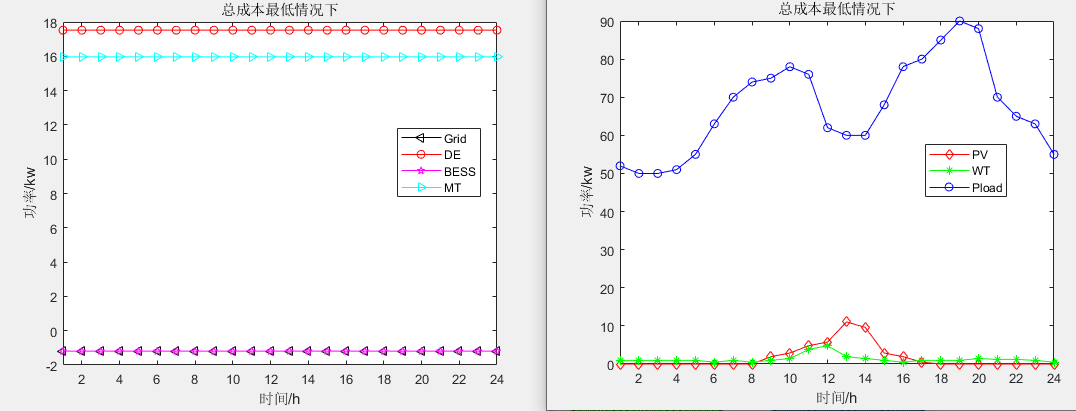
单目标应用:进化场优化算法(Evolutionary Field Optimization,EFO)求解微电网优化MATLAB
一、微网系统运行优化模型 微电网优化模型介绍: 微电网多目标优化调度模型简介_IT猿手的博客-CSDN博客 二、进化场优化算法EFO 进化场优化算法(Evolutionary Field Optimization,EFO)由Baris Baykant Alagoz等人于2022年提出&…...

推荐算法面试
当然可以,请看下面的解释和回答: 一面(7.5) 问题:推荐的岗位和其他算法岗(CV,NLP)有啥区别? 解释: 面试官可能想了解你对不同算法岗位的理解,包…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
