LeetCode|动态规划|1035. 不相交的线 、53. 最大子数组和
目录
一、1035. 不相交的线
1.题目描述
2.解题思路
3.代码实现
二、53. 最大子数组和
1.题目描述
2.解题思路
3.代码实现(动态规划解法)
一、1035. 不相交的线
1.题目描述
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
-
nums1[i] == nums2[j] - 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:
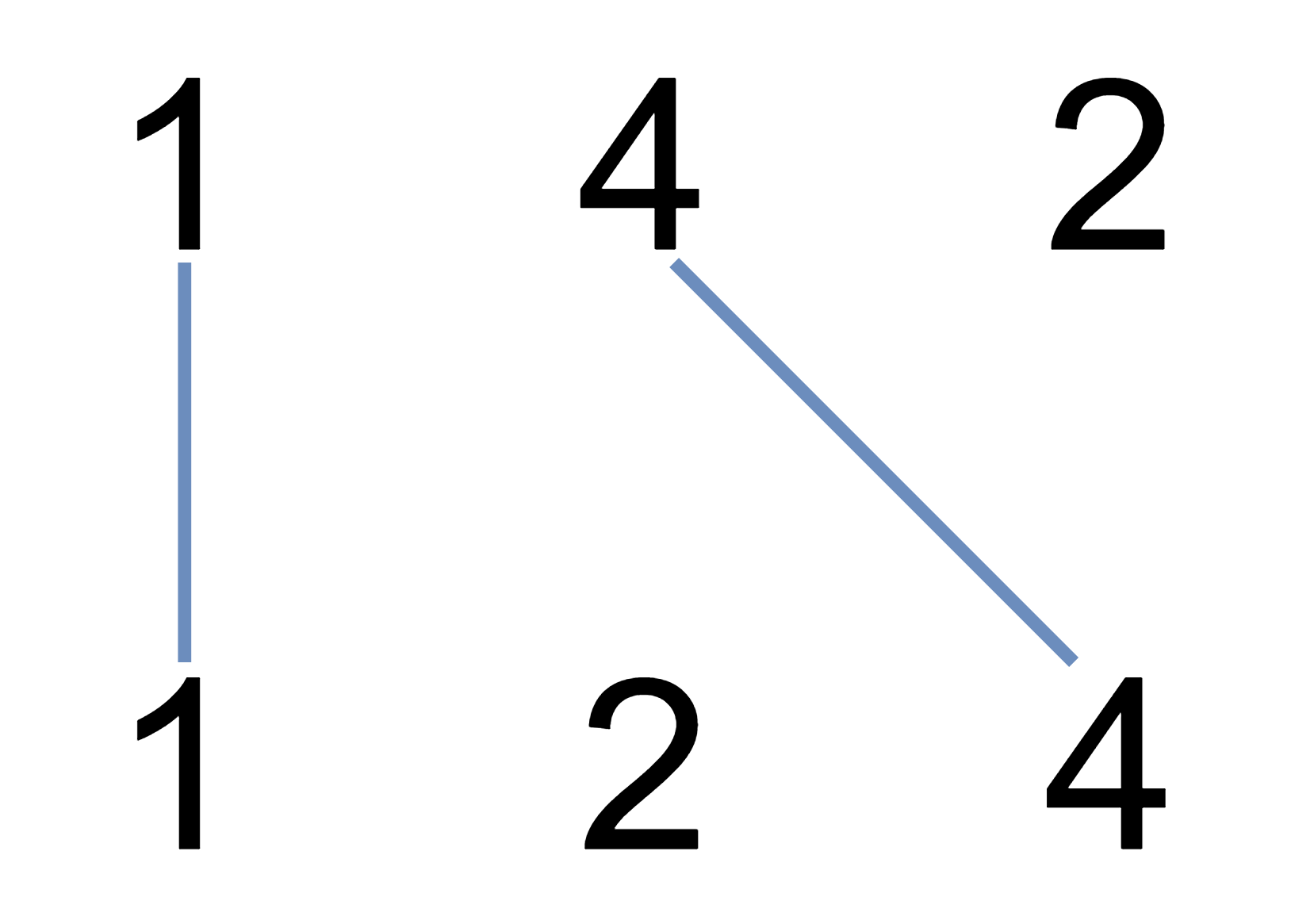
输入:nums1 = [1,4,2], nums2 = [1,2,4] 输出:2 解释:可以画出两条不交叉的线,如上图所示。 但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2] 输出:3
示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1] 输出:2
2.解题思路
- 发现这道题目的本质就不难:两两相等能连线,并且线不能相交。其实就是求最长公共子序列
3.代码实现
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {//这道题的本质就是求最长公共子序列---这里的子序列是不改变数组中的原来相对顺序,并不一定要连续的vector<vector<int>> dp(nums1.size()+1,vector<int>(nums2.size()+1,0));for(int i = 1;i <= nums1.size();i++){for(int j = 1; j <= nums2.size();j++){if(nums1[i-1]== nums2[j-1]){dp[i][j] = dp[i-1][j-1] + 1;}else{dp[i][j] = max(dp[i-1][j],dp[i][j-1]);}}}return dp[nums1.size()][nums2.size()];}
};二、53. 最大子数组和
1.题目描述
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
2.解题思路
- 本题前面发过贪心的解法,现在用动态规划解题
- 详情看代码注释
3.代码实现(动态规划解法)
class Solution {
public:int maxSubArray(vector<int>& nums) {//明确dp数组含义:下标到i为止的,最大和为dp[i]vector<int> dp(nums.size(),0);if(nums.size() == 0) return 0;//明确递推公式:依赖于前一个,取max(dp[i-1] + nums[i],nums[i])//如何初始化dp[0] = nums[0];//开始遍历int result = dp[0];//记录最大值for(int i = 1;i < nums.size();i++){dp[i] = max(dp[i-1]+ nums[i],nums[i]);result = max(result,dp[i]);}return result;}
};相关文章:

LeetCode|动态规划|1035. 不相交的线 、53. 最大子数组和
目录 一、1035. 不相交的线 1.题目描述 2.解题思路 3.代码实现 二、53. 最大子数组和 1.题目描述 2.解题思路 3.代码实现(动态规划解法) 一、1035. 不相交的线 1.题目描述 在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。 现…...
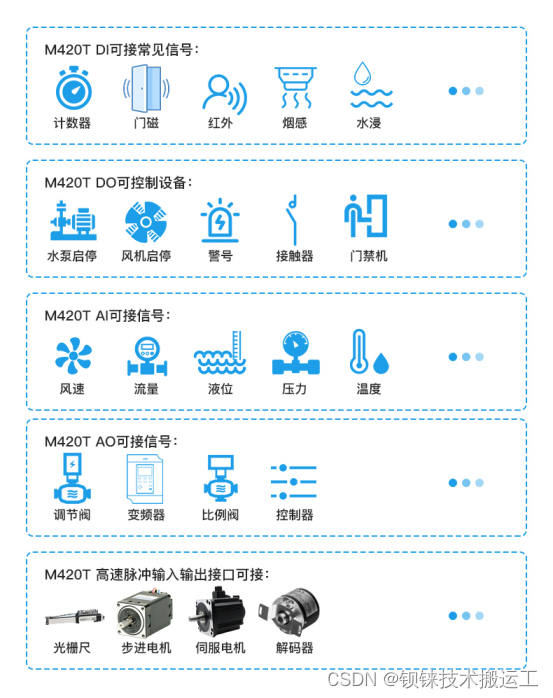
一体式IO模块:汽车行业的数字化转型助推器
随着市场经济需求的不断增长,汽车行业的自动化和智能化已经成为行业发展的必然趋势。在这个背景下,汽车行业的工作流程变得越来越复杂,工业机器人的广泛应用为汽车生产提供了强有力的支持,它们扮演着装配工、操作工、焊接工等多种…...

OpenCV官方教程中文版 —— Hough 直线变换
OpenCV官方教程中文版 —— Hough 直线变换 前言一、原理二、OpenCV 中的霍夫变换三、Probabilistic Hough Transform 前言 目标 • 理解霍夫变换的概念 • 学习如何在一张图片中检测直线 • 学习函数:cv2.HoughLines(),cv2.HoughLinesP() 一、原理…...
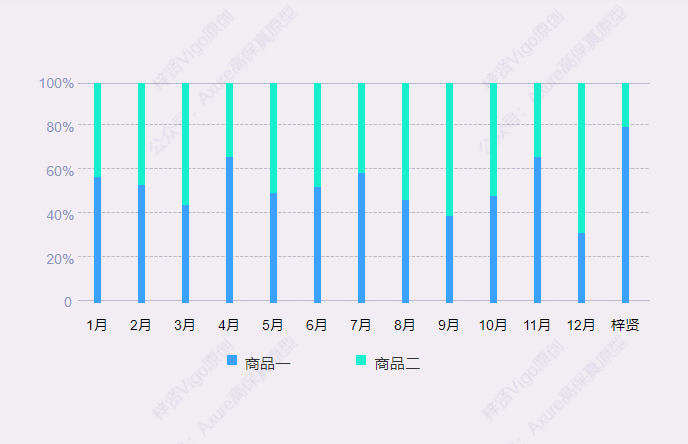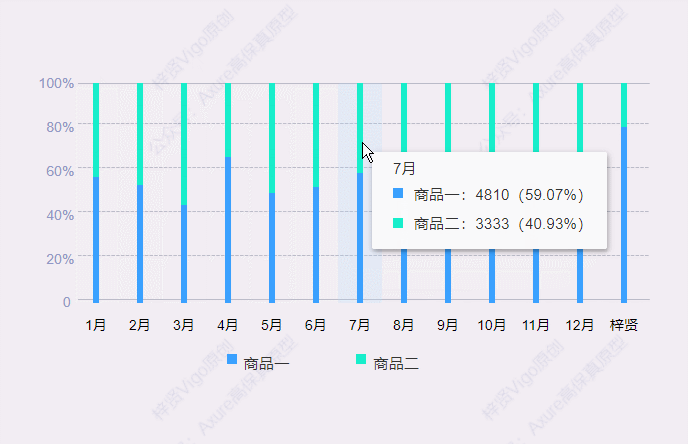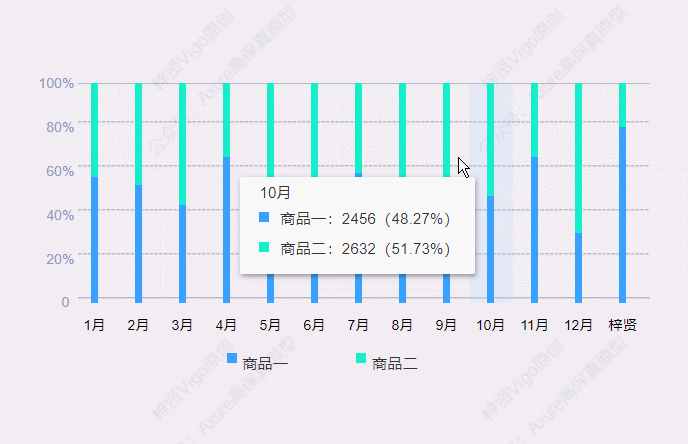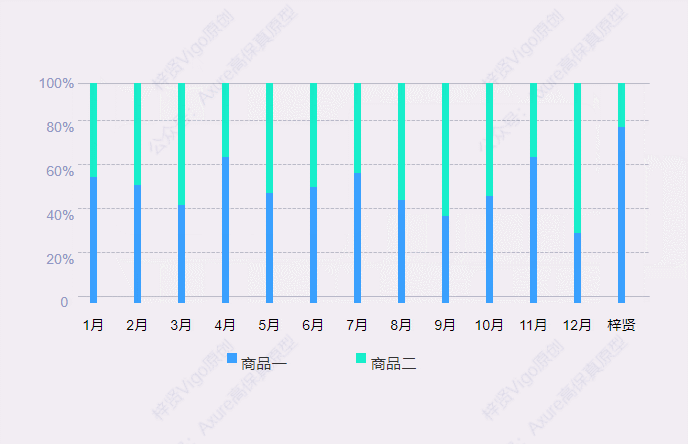
【Axure高保真原型】百分比堆叠柱状图
今天和大家分享百分比堆叠柱状图的的原型模板,鼠标移入堆叠柱状图后,会显示数据弹窗,里面可以查看具体项目对应的数据和占比。那这个原型模板是用中继器制作的,所以使用也很方便,只需要在中继器表格里维护项目数据信息…...

Vue.js中的双向数据绑定(two-way data binding)
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

TFN 2.5G SDH传输分析仪 FT100-D300S
今天给大家带来一款TFN 2.5G SDH传输分析仪--TFN FT100-D300S. D300S SDH测试模块,是FT100智能网络测试平台产品家族的一部分,是一个坚固耐用、锂电池超长供电的传统PDH/SDH测试解决方案,支持2.5Gbps到2.048Mbps速率的传输链路测试。支持在线…...
电脑录像功能在哪?一文帮你轻松破解
“电脑录像功能在哪里呀?最近因工作上的原因,需要使用电脑来录像,但是找了一上午都找不到在哪里,眼看已经快没时间了,现在真的很急,希望大家帮帮我。” 电脑已经成为了人们生活和工作中必不可少的工具&…...

基于长短期神经网络的可上调容量PUP预测,基于长短期神经网络的可下调容量PDO预测,LSTM可调容量预测
目录 背影 摘要 代码和数据下载:基于长短期神经网络的可上调容量PUP预测,基于长短期神经网络的可下调容量PDO预测,LSTM可调容量预测(代码完整,数据齐全)资源-CSDN文库 https://download.csdn.net/download/abc991835105/88230834 LSTM的基本定义 LSTM实现的步骤 基于长短…...

站群服务器有哪些优势?
站群服务器有哪些优势? 站群服务器是单独为一个网站或者多个网站配置独立IP的一种服务器。企业或是用户如果想组建多个网站的话就需要用站群服务器了。 站群服务器可以提高搜索引擎多个网站的关注度,提高网站文章的收录以及网站文章的访问量。站群服务器有哪些优势…...

故障诊断模型 | Maltab实现LSTM长短期记忆神经网络故障诊断
文章目录 效果一览文章概述模型描述源码设计参考资料效果一览 文章概述 故障诊断模型 | Maltab实现LSTM长短期记忆神经网络故障诊断 模型描述 长短记忆神经网络——通常称作LSTM,是一种特殊的RNN,能够学习长的依赖关系。 他们由Hochreiter&Schmidhuber引入,并被许多人进行了…...

【WSL 2】Windows10 安装 WSL 2,并配合 Windows Terminal 和 VSCode 使用
【WSL 2】Windows10 安装 WSL 2,并配合 Windows Terminal 和 VSCode 使用 1 安装 Windows Terminal2 安装 WSL 23 在 Windows 文件资源管理器中打开 WSL 项目4 在 VSCode 中使用 WSL 24.1 必要准备4.2 从 VSCode 中 Connect WSL4.3 从 Linux 中打开 VSCode 1 安装 W…...
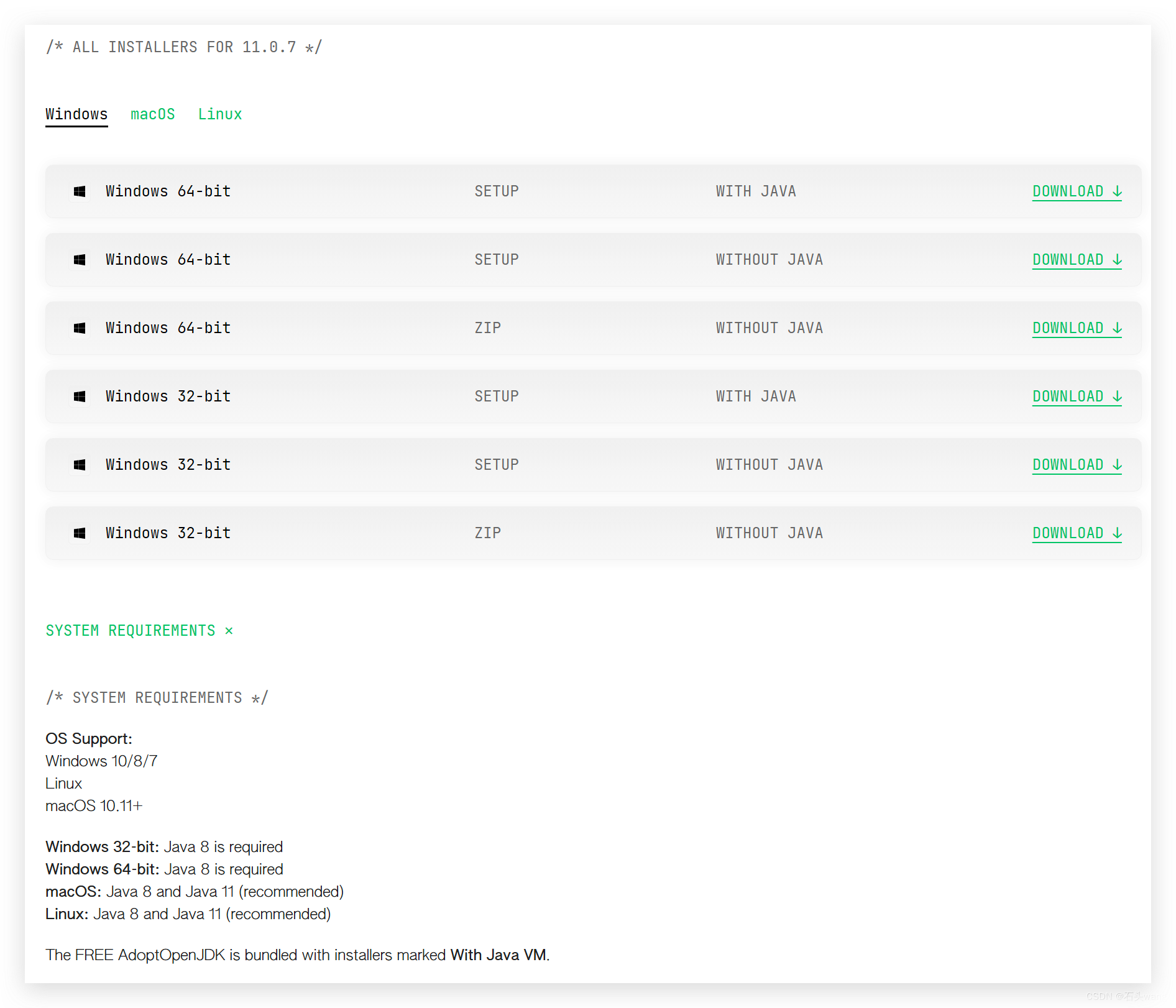
DbVisualizer和DBeaver启动不来,启动报错
启动报错 大多数启动报错都是因为你没有用管理员身份运行程序,提示的错误都是八竿子打不着的什么jdk、jvm问题。 比如DbVisualizer提示什么jvm配置参数,实际dbvis.exe 用管理员身份打开即可(右键 dbvis.exe->属性->兼容性->勾上 “…...
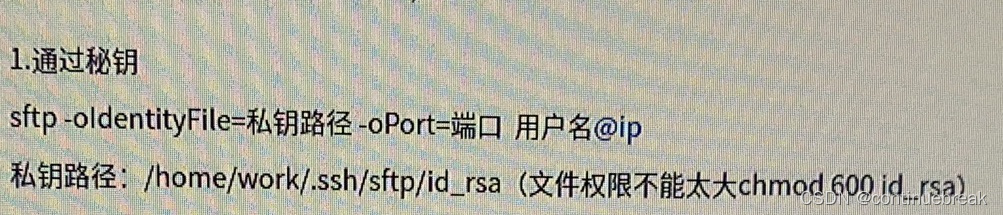
sftp连接远程服务器命令
...

el-select 、el-option 常见用法
<template> <div> // 可以多选 // 添加小叉,点击清空选择器 <el-select v-model"selectedValue" multiple disabled clearable filterable > <el-option …...

奇富科技引领大数据调度革命:高效、稳定、实时诊断
日前,在世界最大的开源基金会 Apache旗下最为活跃的项目之一DolphinScheduler组织的分享活动上,奇富科技的数据平台专家刘坤元应邀为国内外技术工作者献上一场题为《Apache DolphinScheduler在奇富科技的优化实践》的精彩分享,为大数据任务调…...

9.Python3-注释
题记 python3注释 单行注释 # 这是一个注释 print("Hello, World!") 多行注释 单引号 #!/usr/bin/python3 这是多行注释,用三个单引号 这是多行注释,用三个单引号 这是多行注释,用三个单引号print("Hello, World!"…...

内衣洗衣机和手洗哪个干净?好用的内衣洗衣机测评
最近一段时间,关于内衣到底是机洗好,还是手洗好这个话题,有很多人都在讨论,坚决的手洗党觉得应该用手来清洗,机洗与其它衣物混合使用,会产生交叉感染,而且随着使用时间的推移,会变得…...

【MySQL系列】- MySQL日志详解
【MySQL系列】- MySQL日志详解 文章目录 【MySQL系列】- MySQL日志详解一、My日志分类二、重做日志(redo log)redo 日志格式简单日志格式复杂的 redo 日志格式 三、回滚日志(undo log)undo log的作用undo log数据结构 四、二进制日…...
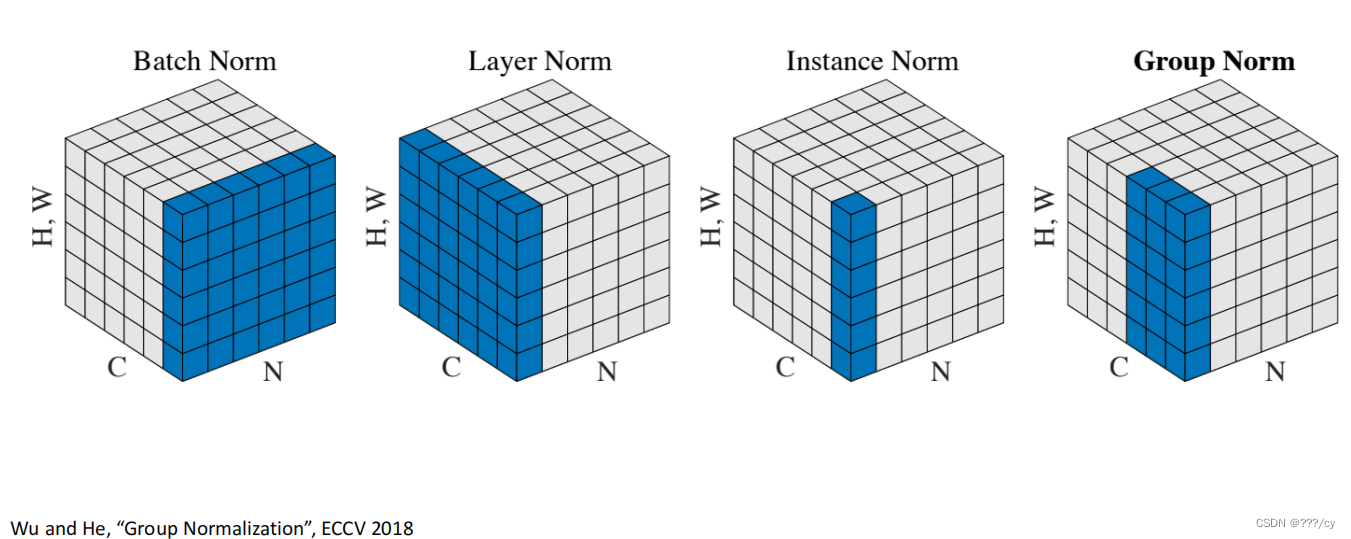
Batch Normalization
文章目录 一,Norimalize(归一化)的想法:二,为什么要做归一化?三,问题来了,如果标准正态分布约束过于严格了怎么办?四,注意:Test-Time五,Batch Nor…...

计算机网络-IP地址
文章目录 子网划分定长子网划分子网划分的方法子网掩码 可变长子网划分 无类别编址网络前缀路由聚合 特殊用途的IP地址专用网络地址链路本地地址运营商级NAT共享地址用于文档的测试网络地址 IP地址的规划和分配IP地址的规划和分配方法IP地址的规划和分配实例 子网划分 定长子网…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
