数据结构与算法-(7)---栈的应用拓展-前缀表达式转换+求值

🌈write in front🌈
🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流.
🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如需转载还请通知⚠️
📝个人主页:Aileen_0v0🧸—CSDN博客
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏:Aileen_0v0🧸的PYTHON学习系列专栏——CSDN博客
🗼我的格言:"没有罗马,那就自己创造罗马~"

目录
回顾+思路讲解
(1)中缀表达式转前缀
(2) 前缀表达式求值
回顾+思路讲解
之前我们介绍过了什么是后缀表达式,以及它如何通过中缀表达式进行转换,以及关于后缀表达式的求值问题,如有遗忘👉🔗http://t.csdnimg.cn/Hl4Y9
今天我们拓展一下,前缀表达式的转换和求值问题

💫中缀转后缀表达式的思路:
从左到右扫描逐个字符扫描中缀表达式的过程中,采用一个栈来暂存未处理的操作符
这样,栈顶的操作符就是最近暂存进去的,当遇到一个新的操作符,就需要跟栈顶的操作符比较下优先级,再行处理--->新符号和栈顶对比,新的高,就入栈(因为取时也先取); 新的低,就把栈顶出栈,让栈顶的先运算想要了解具题后缀的相关知识点点击👉🔗http://t.csdnimg.cn/9100K
中缀转前缀思路也类似,不过
中缀表达式中运算符的优先级和结合性需要考虑,从左往右扫描的话,需要对每个运算符的优先级和结合性进行判断,才能决定是否需要先进行计算。这样会增加算法的复杂度。
而从右往左扫描,则可以利用栈的特性,遇到运算符时先将其压入栈中,再比较栈顶运算符的优先级和结合性,来决定是否需要先进行计算。这样可以简化算法,提高效率。另外,从右往左扫描还可以处理右结合性的运算符。
参考后缀表达式代码思路:
我们利用一个栈来进行中缀表达式转前缀表达式的操作。其中prec{}是一个字典,用于记录操作符的优先级,优先级由低到高依次为1~3。opStack是我们初始化的操作符栈,prefixList是用于储存前缀表达式的空列表。
我们首先将中缀表达式解析为一个tokenList列表,并反转该列表,这样我们就可以正向扫描这个列表。
在扫描过程中,对于每个操作数token,我们需要分别处理三种情况:
- 操作数--将其添加到前缀表达式列表prefixList中。
- 右括号--将其压入操作符栈opStack中。
- 左括号--从操作符栈opStack中弹出并返回顶部元素topToken,直到遇到右括号为止。期间,将所有弹出的操作符添加到前缀表达式列表prefixList中。
对于第4种情况---操作符,
我们需要通过while循环语句比较操作符的优先级。
如果当前操作符的优先级小于等于栈顶操作符的优先级,我们就将栈顶操作符弹出并添加到前缀表达式列表prefixList中。然后将当前操作符压入操作符栈opStack中
(1)中缀表达式转前缀
class Stack :def __init__(self):self.items = []def isEmpty(self):return self.items == []def push(self,item):self.items.append(item)def pop(self):return self.items.pop()def peek(self):return self.items[len(self.items) - 1]def size(self):return len(self.items)def infix_to_prefix(infix_expr):# 定义一个空字典prec{}--记录操作符优先级 -- 优先级由低到高是1~3prec = {}prec["*"] = 3prec["/"] = 3prec["+"] = 2prec["-"] = 2prec[")"] = 1opStack = Stack()#初始化操作符栈#初始化列表用于储存前缀表达式prefixList = []#将中缀表达式解析为一个 tokenList 列表,并反转该列表tokenList = infix_expr.split()[::-1]#利用split切割成一个一个,然后通过切片转置到列表里#列表的元素为:c + ) B + A ( 遇到右括号入栈,左计算for token in tokenList:#若token是操作数---添加到列表if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":prefixList.append(token)# )---压入操作符栈elif token == ")":opStack.push(token)# (---从操作符栈opStack中弹出并返回顶部元素topTokenelif token == "(":topToken = opStack.pop()#当topToken不是")"while topToken != ")":prefixList.append(topToken)topToken = opStack.pop()# 若token是操作符,通过while循环语句比较他们的优先级,大的操作符添加到式子末端else:while (not opStack.isEmpty()) and \(prec[opStack.peek()] > prec[token]):#opStack.pop()会直接把栈顶元素弹出并返回prefixList.append(opStack.pop())opStack.push(token)#扫描完后将栈中的元素弹出while not opStack.isEmpty():# 操作符prefixList.append(opStack.pop())# 将后缀表达式通过切片转置合成前缀表达式字符串return " ".join(prefixList[::-1])
print(infix_to_prefix("A + B * C "))(2) 前缀表达式求值
def postfix_eval(prefix_expr):operandStack = Stack()tokenList = prefix_expr.split()for token in reversed(tokenList):if token in "0123456789":#遇到操作数,入栈operandStack.push(int(token))else:operand2 = operandStack.pop()operand1 = operandStack.pop()result = doMath(token,operand1,operand2)operandStack.push(result)return operandStack.pop()def doMath(op, op1, op2):if op == "*":return op1 * op2elif op == "/":return op1 / op2elif op == "+":return op1 + op2else:return op1 - op2print(doMath("*", 11, 11))定义两个函数:
postfix_eval()和doMath()。
postfix_eval()函数接受一个前缀表达式,将其转换为后缀表达式并计算结果。在计算过程中,它先将操作数入栈,然后遇到运算符就弹出栈顶的两个元素进行计算,并将计算结果重新入栈。最终,栈中仅剩下一个元素,即表达式的计算结果。
doMath()函数用于执行基本的数学运算,包括加、减、乘、除。程序的最后一行在调用
doMath()函数,并输出结果。用于计算11乘以11的结果。

相关文章:

数据结构与算法-(7)---栈的应用拓展-前缀表达式转换+求值
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...

泛型的使用
泛型是一种Java编程语法,它允许我们编写支持多种数据类型的通用类、方法和接口。使用泛型可以使代码更通用、更灵活、更健壮,并提高代码的重用性。 在Java中,泛型的语法使用尖括号<>和类型参数来定义。例如,我们可以定义一…...

docker导致远程主机无法访问,docker网段冲突导致主机网络异常无法访问
背景: 公司分配的虚拟机是172网段的,在上面部署了docker、docker-compose、mysql、redis,程序用docker-compose管理,也平稳运行了一个多周,某天用FinalShell连主机重启docker容器,忽然断开连接,然后虚拟机就…...
Selenium的显性、隐形等待)
Python的web自动化学习(三)Selenium的显性、隐形等待
引言: WebDriver的显性等待和隐形等待是用于在测试过程中等待元素加载或操作完成的两种等待方式。了解此两种方式是为后面自动化找到适合的方法去运用 显性等待(Explicit Wait) 显性等待是通过使用WebDriverWait类和ExpectedConditions类来…...

Linux--文件操作
1.什么是文件 对于文件来说,文件文件内容文件属性;对于文件来说,只有两种操作,对内容的修改和对文件属性的修改,这就是文件的范畴。 对于存放在磁盘上的文件,我们需要通过进程来进行访问,访问文…...
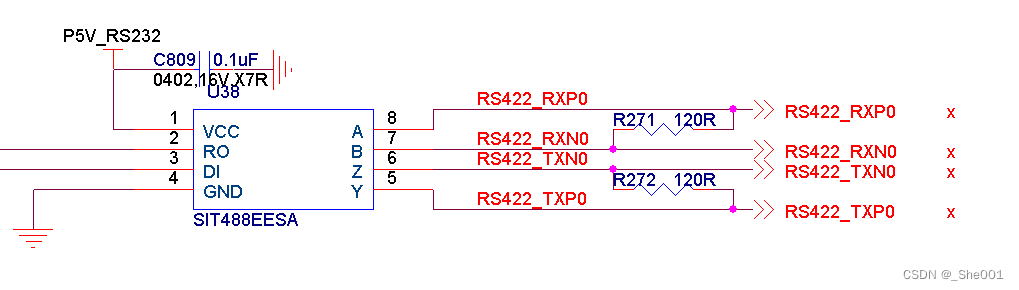
硬件知识积累 RS422接口
1. RS422 基本介绍 EIA-422(过去称为RS-422)是一系列的规定采用4线,全双工,差分传输,多点通信的数据传输协议。它采用平衡传输采用单向/非可逆,有使能端或没有使能端的传输线。和RS-485不同的是EIA-422不允…...
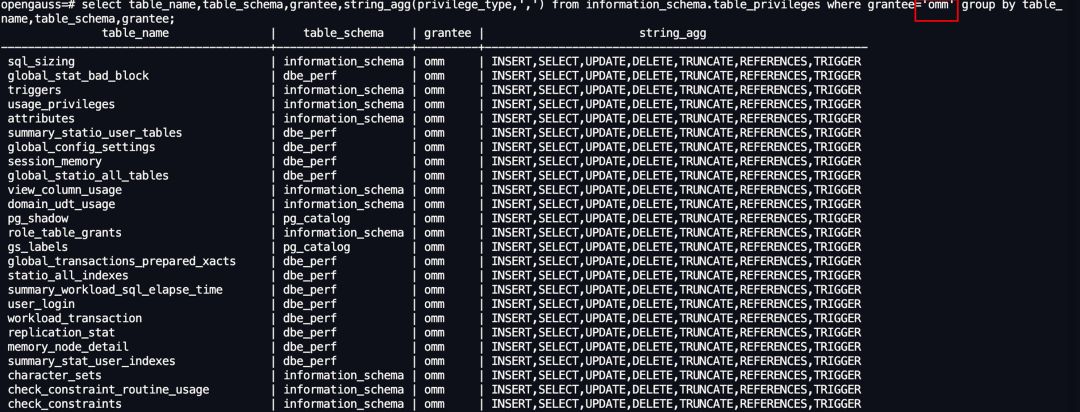
项目经验分享|openGauss 陈贤文:受益于开源,回馈于开源
开源之夏 项目经验分享 2023 #08 # 关于 openGauss 社区 openGauss是一款开源关系型数据库管理系统,采用木兰宽松许可证v2发行。openGauss内核深度融合华为在数据库领域多年的经验,结合企业级场景需求,持续构建竞争力特性。同时openGauss也是…...

实时检测并识别视频中的汽车车牌
对于基于摄像头监控的安全系统来说,识别汽车牌照是一项非常重要的任务。我们可以使用一些计算机视觉技术从图像中提取车牌,然后我们可以使用光学字符识别来识别车牌号码。在这里,我将引导您完成此任务的整个过程。 要求: import cv2import numpy as npfrom skimage impor…...

使用 pyspark 进行 Clustering 的简单例子 -- KMeans
K-means算法适合于简单的聚类问题,但可能不适用于复杂的聚类问题。此外,在使用K-means算法之前,需要对数据进行预处理和缩放,以避免偏差。 K-means是一种聚类算法,它将数据点分为不同的簇或组。Pyspark实现的K-means算法基本遵循以下步骤: 随机选择K个点作为初始质心。根…...

LeetCode75——Day22
文章目录 一、题目二、题解 一、题目 1657. Determine if Two Strings Are Close Two strings are considered close if you can attain one from the other using the following operations: Operation 1: Swap any two existing characters. For example, abcde -> aec…...
【SOC基础】单片机学习案例汇总 Part1:电机驱动、点亮LED
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...

【HTML】HTML基础知识扫盲
1、什么是HTML? HTML是超文本标记语言(Hyper Text Markup Language)是用来描述网页的一种语言 注意: HTML不是编程语言,而是标记语言 HTML文件也可以直接称为网页,浏览器的作用就是读取HTML文件ÿ…...
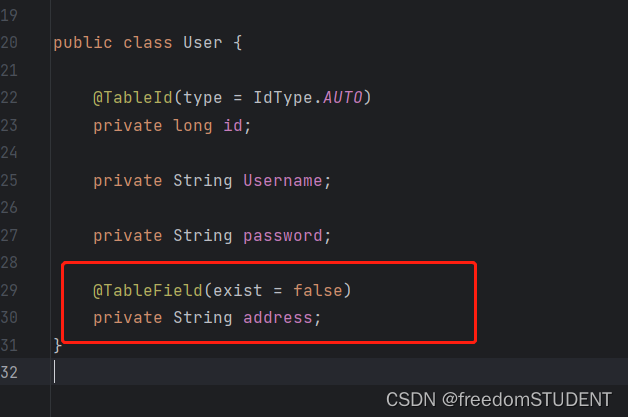
【Mybatis-Plus】常见的@table类注解
目录 引入Mybatis-Plus依赖 TableName 当实体类的类名在转成小写后和数据库表名相同时 当实体类的类名在转成小写后和数据库表名不相同时 Tableld TableField 当数据库字段名与实体类成员不一致 成员变量名以is开头,且是布尔值 编辑 成员变量名与数据库关…...
)
Android WMS——操作View(七)
上一篇文章我们将 view 传递给 ViewRootImpl 进行操作,这里我们主要分析 ViewRootImpl 对 View 进行操作。在正式分析之前我们先来介绍以下 View。 一、View介绍 最开始学习 View 的时候最先分析的是它的布局(LinearLayout、FrameLayout、TableLayout、RelativeLayout、Abso…...

算法__数组排序_冒泡排序直接选择排序快速排序
文章目录 冒泡排序算法说明代码实现 直接选择排序算法说明代码实现 快速排序算法说明代码实现 本篇主要讲解数组排序相关的三种算法,冒泡排序,直接排序和快速排序。 冒泡排序 算法说明 在数组中依次比较相邻的两个元素,当满足左侧大于右侧时…...
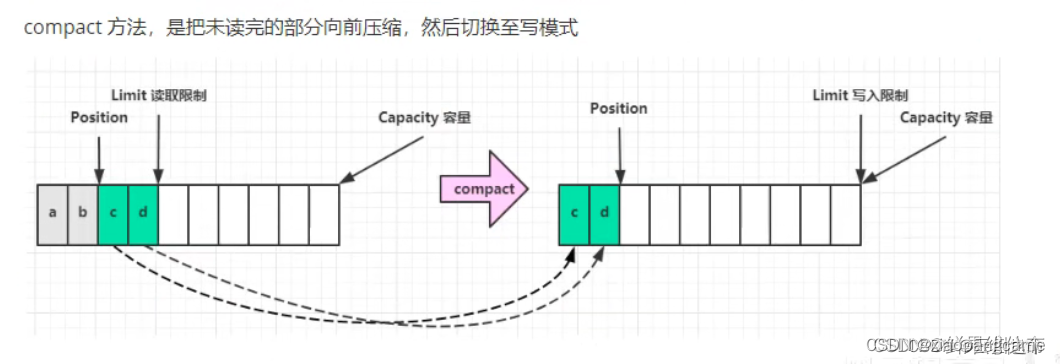
ByteBuffer的原理和使用详解
ByteBuffer是字节缓冲区,主要用户读取和缓存字节数据,多用于网络编程,原生的类,存在不好用,Netty采用自己的ByteBuff,对其进行了改进 1.ByteBuffer的2种创建方式 1.ByteBuffer buf ByteBuffer.allocate(i…...

【MySql】10- 实践篇(八)
文章目录 1. 用动态的观点看加锁1.1 不等号条件里的等值查询1.2 等值查询的过程1.3 怎么看死锁?1.4 怎么看锁等待?1.5 update 的例子 2. 误删数据后怎么办?2.1 删除行2.2 误删库/表2.3 延迟复制备库2.4 预防误删库 / 表的方法2.4.1 账号分离2.4.2 制定操…...
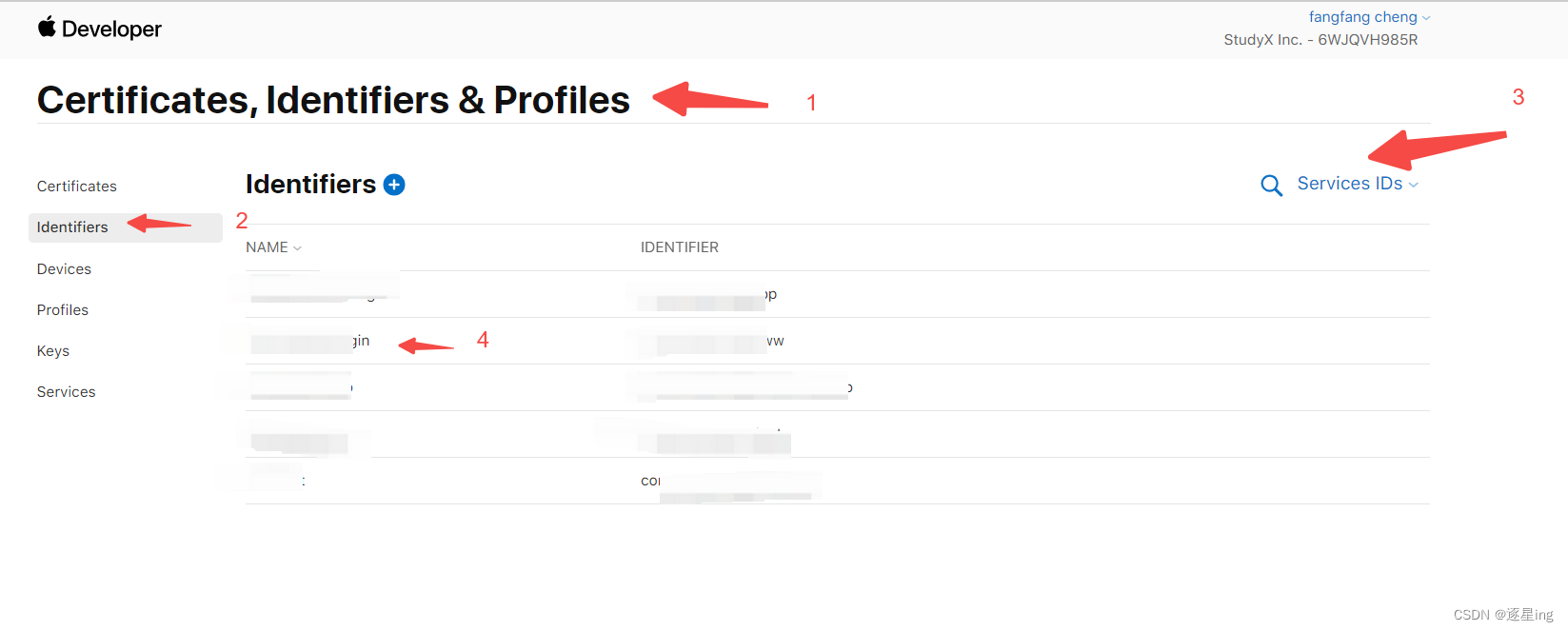
【三方登录-Apple】iOS 苹果授权登录(sign in with Apple)之开发者配置一
记录一下sign in with Apple的开发者配置 前言 关于使用 Apple 登录 使用“通过 Apple 登录”可让用户设置帐户并使用其Apple ID登录您的应用程序和关联网站。首先使用“使用 Apple 登录”功能启用应用程序的App ID 。 如果您是首次启用应用程序 ID 或为新应用程序启用应用程序…...

可视化 | 数据可视化降维算法梳理
文章目录 📚数据描述🐇iris🐇MNIST 📚PCA🐇算法流程🐇图像描述 📚Kernel-PCA🐇算法流程🐇图像描述 📚MDS🐇算法流程🐇图像描述 &#…...
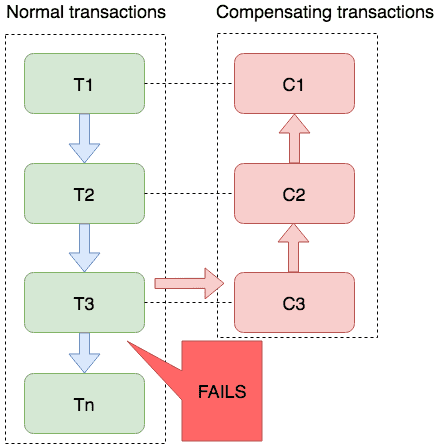
分布式:一文吃透分布式事务和seata事务
目录 一、事务基础概念二、分布式事务概念什么是分布式事务分布式事务场景CAP定理CAP理论理解CAPCAP的应用 BASE定理强一致性和最终一致性BASE理论 分布式事务分类刚性事务柔性事务 三、分布式事务解决方案方案汇总XA规范方案1:2PC第一阶段:准备阶段第二…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
