哈夫曼树c语言版
一、哈夫曼树概念
哈夫曼树又称最优树给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
例给定一个有序数组{3,5,6,9,10},构造出一个哈夫曼树如下:
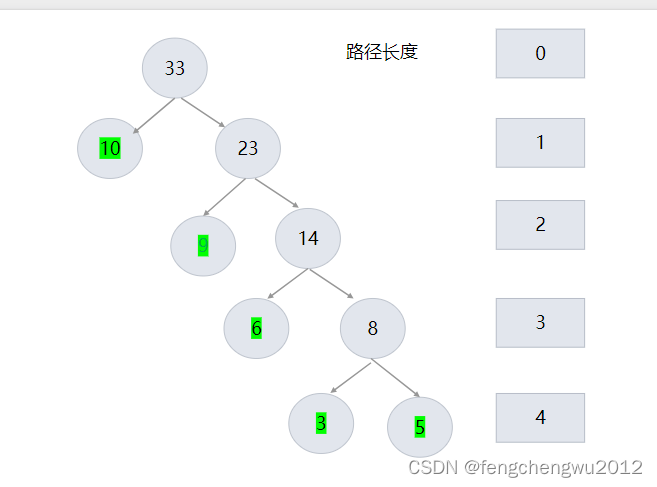
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL
WPL = (3+5)*4 + 6*3 + 9*2 +10*1 = 98
二、实现代码
1、定义树结点
typedef struct huffmantreenode
{int* data;struct huffmantreenode* leftNode;struct huffmantreenode* rightNode;
} HuffmanTree;2、声明函数操作
/***创建节点
*/
HuffmanTree* create_huffman_tree(int data);/*** 初始化哈夫曼根节点
*/
HuffmanTree* create_huffman_tree_root(int first,int second);/*** 新增节点
*/
void insert_huffmantree_node(HuffmanTree** tree,int data);/*** 前序遍历
*/
void pre_oder_huffmantree(HuffmanTree** tree);/*** 销毁树
*/
void destroy_huffmantree(HuffmanTree* tree);3、函数定义
HuffmanTree* create_huffman_tree(int data)
{HuffmanTree* node = malloc(sizeof(HuffmanTree*));if(node==NULL){perror("节点点申请内存失败");return NULL;}node->data = malloc(sizeof(int*));*(node->data) = data;node->leftNode = NULL;node->rightNode = NULL;return node;
}HuffmanTree* create_huffman_tree_root(int first,int second)
{HuffmanTree* firstNode = create_huffman_tree(first);HuffmanTree* secondNode = create_huffman_tree(second);HuffmanTree* root = create_huffman_tree(first+second);root->leftNode = firstNode;root->rightNode = secondNode;return root;
}void insert_huffmantree_node(HuffmanTree** tree,int data)
{HuffmanTree* root = *tree;if(root==NULL){perror("初始结点为空");return;}int rootData = *(root->data);HuffmanTree* node = create_huffman_tree(data); HuffmanTree* newRoot = create_huffman_tree(data+rootData); bool isLeft = rootData<data;newRoot->leftNode = isLeft?root:node;newRoot->rightNode = isLeft?node:root;*tree = newRoot;
}void pre_oder_huffmantree(HuffmanTree** tree)
{HuffmanTree* curNode = *tree;if(curNode==NULL){return;}printf("前序遍历sort=%d\n",*(curNode->data));pre_oder_huffmantree(&(curNode->leftNode));pre_oder_huffmantree(&(curNode->rightNode));
}void destroy_huffmantree(HuffmanTree* tree)
{if(tree==NULL){return;}destroy_huffmantree(tree->leftNode);destroy_huffmantree(tree->rightNode);free(tree);
}4、测试函数
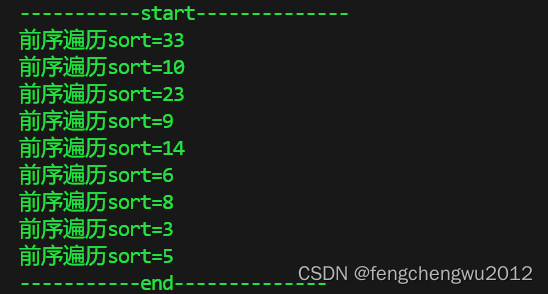
void test_huffmantree()
{int arr[] = {3,5,6,9,10};HuffmanTree* root = create_huffman_tree_root(arr[0],arr[1]);int i = 2;for(;i<5;i++){insert_huffmantree_node(&root,arr[i]);}pre_oder_huffmantree(&root);destroy_huffmantree(root);
}
相关文章:

哈夫曼树c语言版
一、哈夫曼树概念 哈夫曼树又称最优树给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大…...
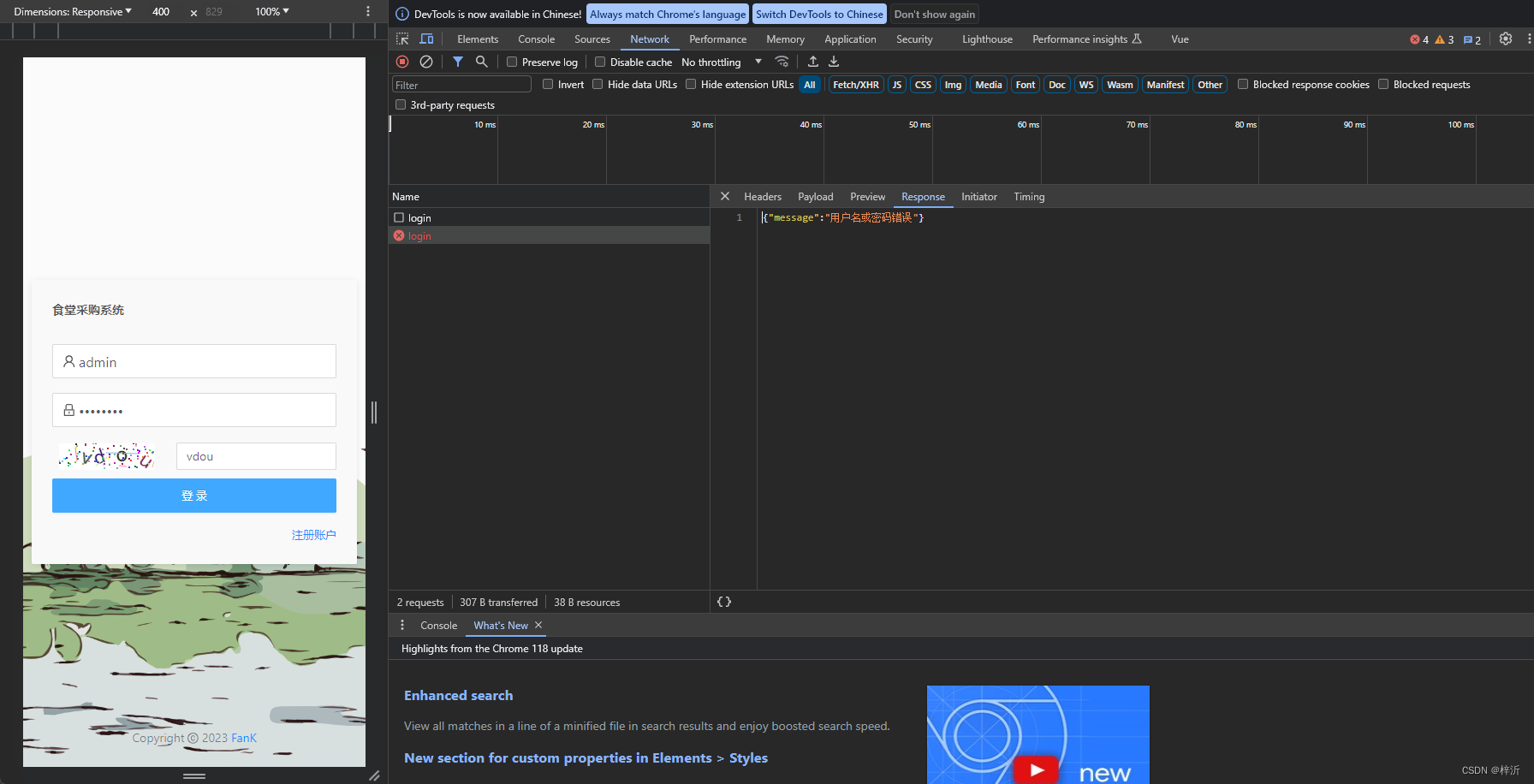
食堂系统登录报错
因为数据库没有任何用户数据,所以会报错,需要添加admin用户 D:\env\jdk1.8.0_341\bin\java.exe -XX:TieredStopAtLevel1 -noverify -Dspring.output.ansi.enabledalways -Dcom.sun.management.jmxremote -Dspring.jmx.enabledtrue -Dspring.liveBeansVie…...

uniapp原生插件之乐橙摄像机播放插件(子账号云台对讲版)
插件介绍 乐橙摄像机播放插件(云台对讲版),集成视频播放,对讲模式、云台控制 插件地址 乐橙摄像机播放插件(子账号云台对讲版) - DCloud 插件市场 超级福利 uniapp 插件购买超级福利 插件申请权限 麦克风权限(可参考示例项目ÿ…...

Http代理与socks5代理有何区别?如何选择?(一)
了解SOCKS和HTTP代理之间的区别对于优化您的在线活动至关重要,无论您是技术娴熟的个人、现代互联网用户还是企业所有者。在使用代理IP时,您需要先了解这两种协议之间的不同。 一、了解HTTP代理 HTTP(超文本传输协议)代理专门设计…...

system verilog VSCode Windows 配置简述
system verilog VSCode Windows 配置简述 本文章的目的并非完全在 VSCode 中进行 system verilog 编程,而是以 vivado 为核心,将 VSCode 作为编译器。 配置步骤 安装 ctags choco install universal-ctags如果你没有安装 chocolatey,见 i…...
Linux中的Shell编程
Linux中的Shell编程 shell编程快速入门 为什么要学习Shell编程? 1.Linux运维工程师在进行服务器集群管理时,需要编写Shell程序来进行服务器管理。 2.对于JavaEE和Python程序员来说,工作的需要,你的老大会要求你编写一些Shell脚本…...

图像特征Vol.1:计算机视觉特征度量|第二弹:【统计区域度量】
目录 一、前言二、统计区域度量2.1:图像矩特征2.1.1:原始矩/几何矩2.1.2:中心距2.1.3:归一化的中心矩2.1.4:不变矩——Hu矩2.1.5:OpenCv实现矩特征及其应用 2.2:点度量特征2.3:全局直…...

将图像的锯齿状边缘变得平滑的方法
项目背景 使用PaddleSeg 192x192 模型分割出来的目标有锯齿状边缘,想通过传统算法将这种锯齿状边缘的变得平滑,虽然试了很过方法,但是效果还是不太理想 常用的集中方法 当使用分割算法(如分水岭分割、阈值分割等)分…...

【MySQL索引与优化篇】数据库设计实操(含ER模型)
数据库设计实操(含ER模型) 文章目录 数据库设计实操(含ER模型)1. ER模型1.1 概述1.2 建模分析1.3 ER 模型的细化1.4 ER 模型图转换成数据表1. 一个实体转换成一个数据库表2. 一个多对多的关系转换成一个数据表3. 通过外键来表达1对…...
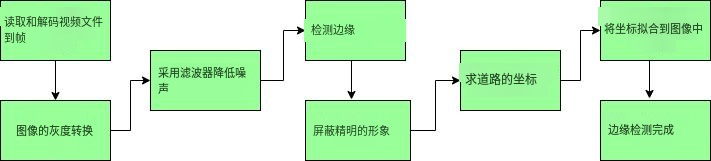
OpenCV—自动驾驶实时道路车道检测(完整代码)
自动驾驶汽车是人工智能领域最具颠覆性的创新之一。在深度学习算法的推动下,它们不断推动我们的社会向前发展,并在移动领域创造新的机遇。自动驾驶汽车可以去传统汽车可以去的任何地方,并且可以完成经验丰富的人类驾驶员所做的一切。但正确地训练它是非常重要的。自动驾驶汽…...
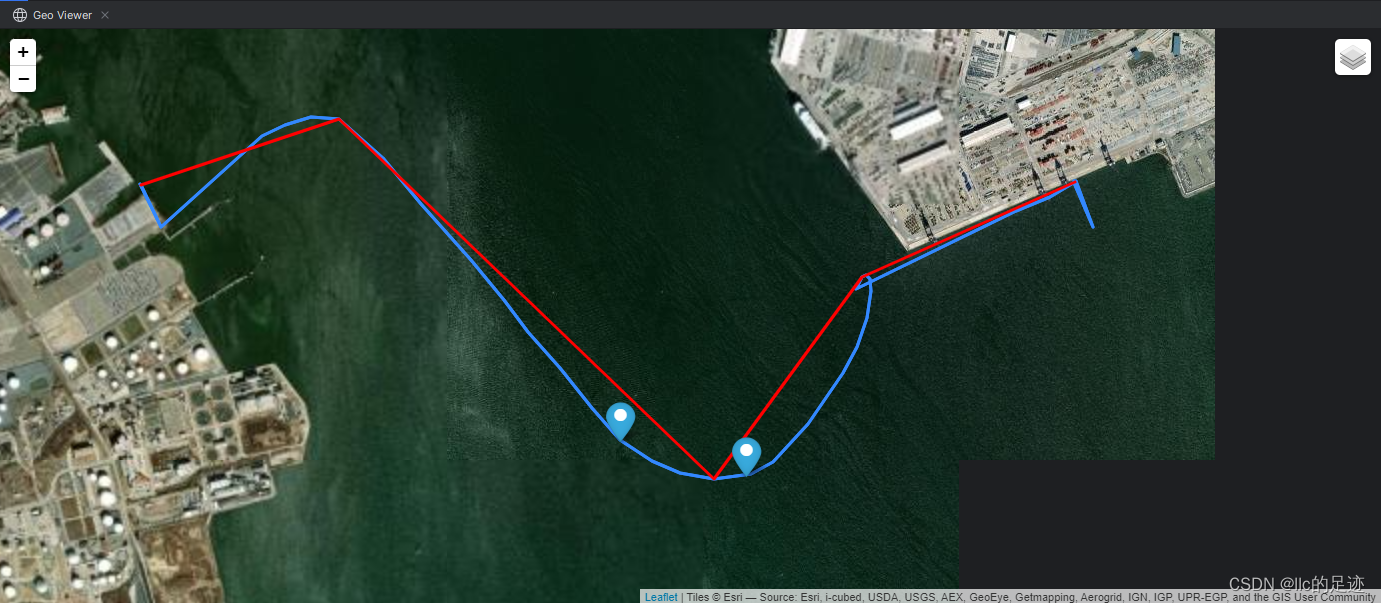
PostGIS轨迹分析——简化轨迹
需求 对轨迹线进行简化,并将原始轨迹上的两个特征点拉取到简化后的轨迹上 简化线 红色线是简化后的轨迹线,蓝色线是原始轨迹,有两个特征点 知识点: st_makeline函数将点连成线st_simplify简化线函数,其中第二个参数为坐标系的单位,0.002度大概代表0.002x1.11x10^5≈22…...

量化交易-应对市场闪崩
金融交易世界虽然提供了无与伦比的机会,但也并非没有陷阱。其中一个陷阱是闪崩现象,尤其是在算法交易领域。这些快速且常常无法解释的市场下跌可能会在几分钟内消除数十亿美元的价值。了解它们的起源、影响和预防策略对于参与算法交易的任何人都至关重要。本文深入研究了闪存…...

在Vue3+ElementPlus项目中使用具有懒加载的el-tree树形控件
前言 有时遇到一些需求就是在使用树形控件时,服务端并没有一次性返回所有数据,而是返回首层节点列表。然后点击展开首层节点中的某个节点,再去请求该节点的子节点列表,那么就得用上懒加载的机制了。在此以ElementPlus的树形控件为…...

高浓度工业废水处理设备有哪些
高浓度工业废水处理设备主要有以下几种: 水解酸化池:将有机废水通过水解、酸化作用,使其成为更易于生化降解的有机物。厌氧池:通过厌氧反应降解有机废水,产生沼气等可再利用资源。好氧池:将经过水解酸化或…...

linux上传mysql数据库
如果你使用的是Linux操作系统,并且需要上传MySQL数据库,那么可以按照以下步骤进行操作: 1. 在终端登录到你的Linux服务器; 2. 运行以下命令,以安装MySQL客户端:sudo apt-get install mysql-client…...

easyexcel根据模板导出Excel文件,表格自动填充问题
背景 同事在做easyexcel导出Excel,根据模板导出的时候,发现导出的表格,总会覆盖落款的内容。 这就很尴尬了,表格居然不能自动填充,直接怒喷工具,哈哈。 然后一起看了一下这个问题。 分析原因 我找了自…...

golang调用智能合约,获取合约函数的返回值
如果不是只读取数据的合约函数,需要异步的执行,因此并不能直接获取到合约函数的返回值,需要等到交易执行完毕,得到确认后才能获取到合约函数的返回值。而且合约函数返回值一般是通过事件日志获取到的。 这里给出一个例子来展示我…...
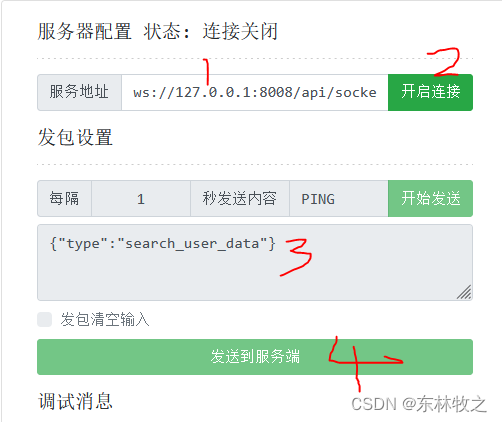
Django3框架-(3)-[使用websocket]:使用channels实现websocket功能;简化的配置和实际使用方式
概述: 对于Django使用channels实现websocket的功能,之前就写了几篇博文了。随着在项目的使用和实际维护来说,重新设置了相关处理方法。 一般来说,前后端都只维护一个全局的连接,通过携带数据来判断具体的操作&#x…...

java-工具类抛异常
不满足条件就会报错,这里的accessors ! null,就是等于空的时候(不满足)就会报错 accessors null; Assert.isTrue(ObjectUtil.isNotEmpty(accessors ! null), "数据为空");...
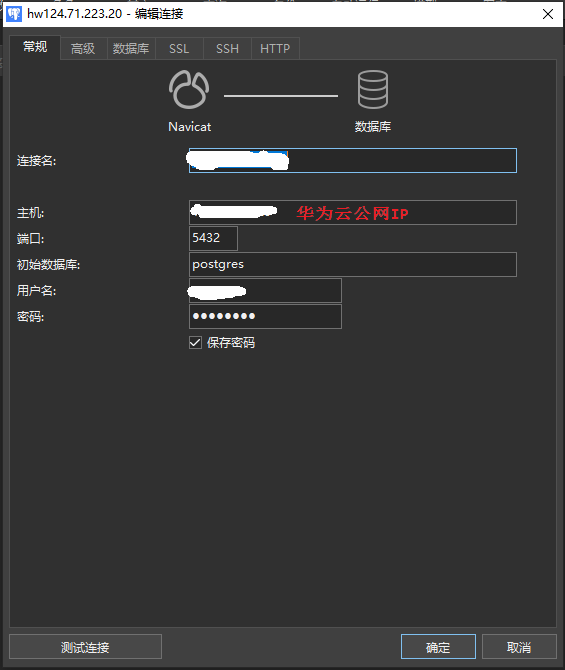
Navicat连接postgresql数据库 -->华为云服务器
Navicat连接postgresql数据库 -->华为云服务器 2.开放服务器端口:54323.Navicat连接postgresql数据库 2.开放服务器端口:5432 1-1.选择安全组 1-2. 添加规则 1-3.开放5432端口规则 1-4.查看规则 3.Navicat连接postgresql数据库...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
