深度学习_3 数据操作之线代,微分
线代基础
标量
只有一个元素的张量。可以通过 x = torch.tensor(3.0) 方式创建。
向量
由多个标量组成的列表(一维张量)。比如 x = torch.arange(4) 就是创建了一个1*4的向量。可以通过下标获取特定元素(x[3]),可以通过 len(x) 获取长度,可以通过 x.shape 获取形状。
矩阵
二维张量,比如 reshape(a,b) 后得到的张量。
可以通过 X.T 转置。
张量运算
相同形状的张量二元运算是标量,向量,矩阵运算的扩展。
加法:所有元素分别求和。
乘法:对应位置元素分别相乘。
加标量/乘标量:所有元素分别加/乘标量。
降维
sum() 是可以实现降维操作的。A.sum() 是直接沿所有维度求和得到一个标量。还可以指定维度求和进行降维。
A
# Output
(tensor([[ 0., 1., 2., 3.],[ 4., 5., 6., 7.],[ 8., 9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]]),A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
# Output
(tensor([40., 45., 50., 55.]), torch.Size([4]))A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
# Output
(tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))A.sum(axis=[0, 1]) # 结果和A.sum()相同
# Output
tensor(190.)
总和也可以用 A.mean() 或者 A.sum()/A.numel() 来算。
也可以利用 A.mean(axis=0) 或 A.sum(axis=0)/A.shape[0] 来降低维度。
非降维求和
sum_A = A.sum(axis=1, keepdims=True)
sum_A
# Output
tensor([[ 6.],[22.],[38.],[54.],[70.]])A / sum_A # 广播操作
# Output
tensor([[0.0000, 0.1667, 0.3333, 0.5000],[0.1818, 0.2273, 0.2727, 0.3182],[0.2105, 0.2368, 0.2632, 0.2895],[0.2222, 0.2407, 0.2593, 0.2778],[0.2286, 0.2429, 0.2571, 0.2714]])A.cumsum(axis=0) # 按行求和且不降维
# Output
tensor([[ 0., 1., 2., 3.],[ 4., 6., 8., 10.],[12., 15., 18., 21.],[24., 28., 32., 36.],[40., 45., 50., 55.]])
矩阵乘法
左矩阵逐列和右矩阵逐行相乘。
torch.mv(a,b)
范数
向量的大小。
L1范数:各个分量绝对值长度求和。
L2范数:欧几里得长度(比如二维向量是a2+b2 开根)。
Frobenius范数:矩阵中每一个元素的平方和开根。
微积分
微分
导数的基本概念就不详细叙述了,这是大学必修课。
常用公式:
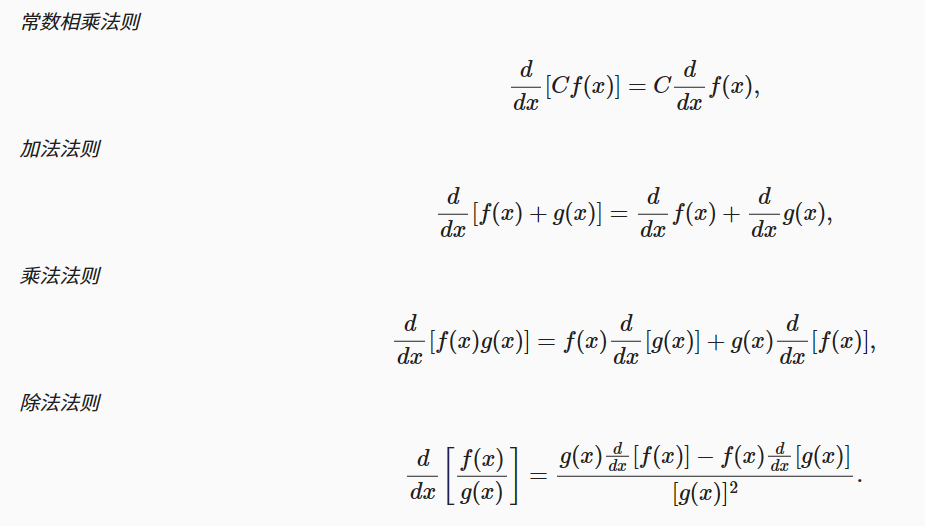
自动微分
python 里是自动求导,一个函数在指定值上做求导。
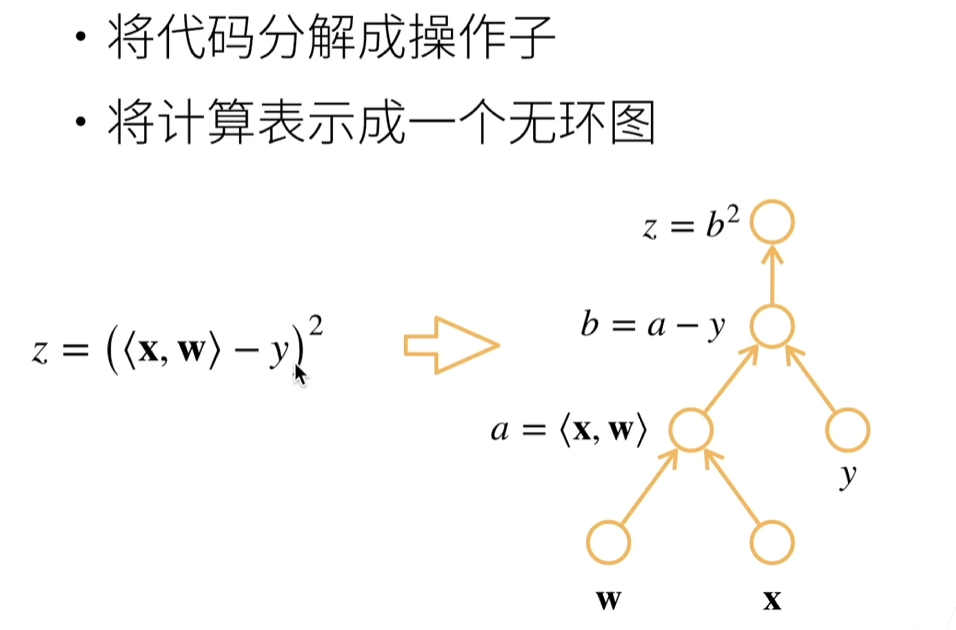
正向传递:如上图,先计算 w 关于 x 的导数,在计算 b 关于 a 的导数……
反向传递:全过程正好相反,先计算 z 关于 b 的导数,再计算 b 关于 a 的导数……
正向反向累积的时间复杂度都是 O(N),但是正向空间复杂度是 O(1),反向一直要把所有的中间结果记录下来,空间复杂度 O(N)。
显示构造:先定义公式,再赋值。

隐式构造:pytorch 采用的是这种方案。

下面展开一个具体的计算例子。比如我们要计算 y=2x2 的导数。
# 先创建 x
from mxnet import autograd, np, npx
npx.set_np()
x = np.arange(4.0) #[0. ,1. ,2. ,3.]
x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
# 在计算关于x的梯度后,将能够通过'grad'属性访问它,它的值被初始化为 [0. ,0. ,0. ,0.]
y = 2 * torch.dot(x, x)
y.backward()
x.grad # [0. ,4. ,8. ,12.]
# y 的导数在这几个点上应该是 4x。验证一下是否正确
x.grad == 4 * x # [True,True,True,True]# 再算一下另一个函数
x.grad.zero_() # 清零
y=x.sum() # x_1+x_2+...+x_n
y.backward()
x.grad # [1. ,1. ,1. ,1.]x.grad.zero_() # 清零
y = x * x # y是一个向量,注意这里是哈马达积,和前面的点积不一样。点积得到的是一个标量,这个是每个x对应彼此相乘得到的1*4的向量
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad # 等价于y=sum(x*x) [0. ,2. ,4. ,8.]# 分离计算:比如z=u*x, u=x*x,但是我们不想把 u 展开求导,我们期望对 z 求 x 导数得到 u
x.grad.zero_()
y = x * x
u = y.detach() # 相当于 requires_grad = False,不会得到梯度
z = u * x
z.sum().backward()
x.grad == u# 自动微分也可以计算包含条件分支的分段。以下分段本质上都是k*a。
def f(a):b = a * 2while b.norm() < 1000:b = b * 2if b.sum() > 0:c = belse:c = 100 * breturn c
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
a.grad == d / a # True
相关文章:

深度学习_3 数据操作之线代,微分
线代基础 标量 只有一个元素的张量。可以通过 x torch.tensor(3.0) 方式创建。 向量 由多个标量组成的列表(一维张量)。比如 x torch.arange(4) 就是创建了一个1*4的向量。可以通过下标获取特定元素(x[3]),可以通…...
树莓派安装Ubuntu22.04LTS桌面版
工具:树莓派4B Raspberry Pi 自己下载的ubuntu22.04LTS img磁盘镜像文件 这里有一个小技巧:这个Raspberry Pi的选择镜像的时候在最后面一行可以选择自定义的镜像,哈哈哈哈,这就使得我们可以自己下载,而且知道那个文…...
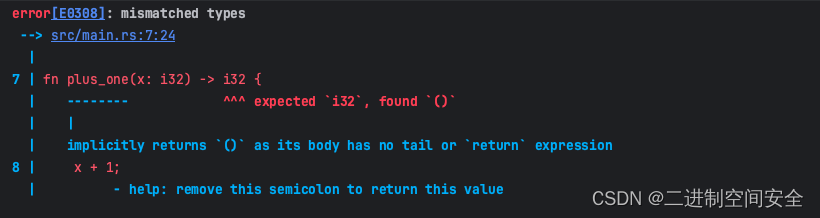
Rust编程基础之函数和表达式
1.Rust函数 在之前的文章中,我们已经见到了一个函数:main函数, 它是很多程序的入口点。也见过 fn 关键字,它用来声明新函数。 Rust 代码中的函数和变量名使用 snake case 规范风格。在 snake case 中,所有字母都是小写并使用下划线分隔单词。这是一个包…...

关于preempt count的疑问
Linux中的preempt_count - 知乎 https://www.cnblogs.com/hellokitty2/p/15652312.html LWN:关于preempt_count()的四个小讨论!-CSDN博客 主要是参考这些文章 之前一直认为只要是in_interrupt()返回非0值,那么就可以认为当前在中断上下文。即…...

Windows 开启 Kerberos 的火狐 Firefox 浏览器访问yarn、hdfs
背景:类型为IPA或者MIT KDC,windows目前只支持 firefoxMIT Kerberos客户端的形式,其他windows端浏览器IE、chrome、edge,没有办法去调用MIT Kerberos Windows客户端的GSSAPI验证方式,所以均无法使用 Windows 开启 Kerb…...
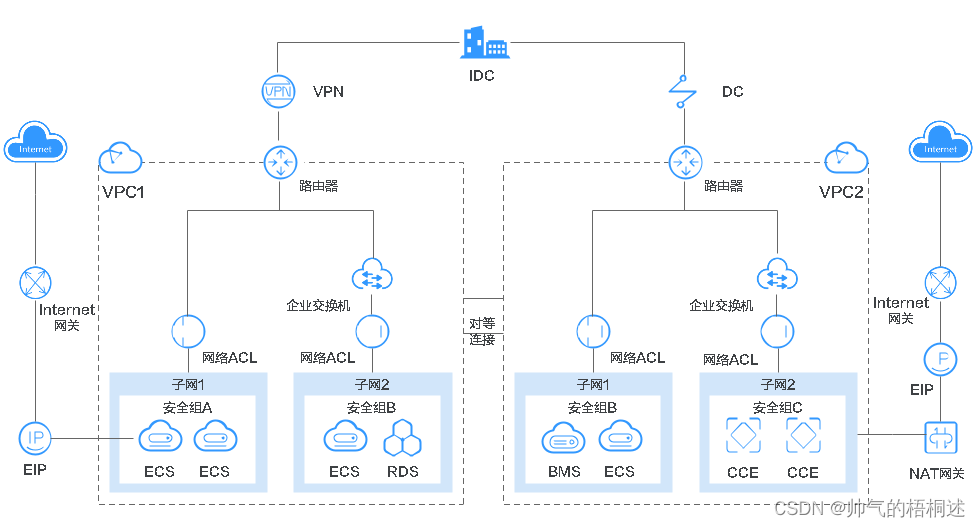
华为云资源搭建过程
网络搭建 EIP: 弹性EIP,支持IPv4和IPv6。 弹性公网IP(Elastic IP)提供独立的公网IP资源,包括公网IP地址与公网出口带宽服务。可以与弹性云服务器、裸金属服务器、虚拟IP、弹性负载均衡、NAT网关等资源灵活地绑定及解绑…...

突破防火墙的一种方法
当Linux防火墙阻止来自某个ip的数据时,它应该是根据ip数据报里“源IP地址”字段取得的对方ip吧,那对方就不能通过篡改“源IP地址”来绕过防火墙吗?NAT模式下的路由器就修改了这个字段。 但这样的话,攻击者是收不到服务器返回的数…...
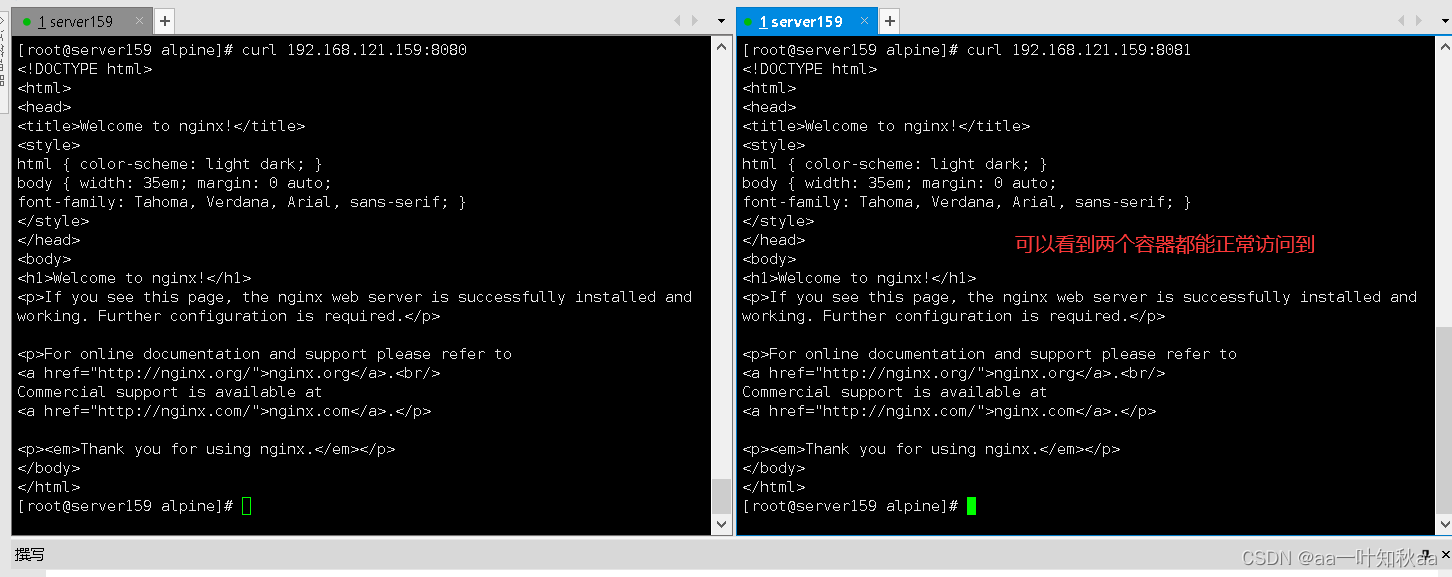
Docker 多阶段构建的原理及构建过程展示
Docker多阶段构建是一个优秀的技术,可以显著减少 Docker 镜像的大小,从而加快镜像的构建速度,并减少镜像的传输时间和存储空间。本文将详细介绍 Docker 多阶段构建的原理、用途以及示例。 Docker 多阶段构建的原理 在传统的 Docker 镜像构建…...

【开题报告】基于Spring Boot的家装产品展示交易平台的设计与实现
1.研究背景和目的 随着人们对居住环境舒适度和个性化需求的不断提升,家装市场正逐渐发展成为一个重要的消费领域。为了满足消费者对家装产品的需求,建立一个高效、可靠的家装产品展示交易平台变得尤为重要。本项目旨在通过使用Spring Boot框架ÿ…...

MacOS安装git
文章目录 通过Xcode Command Lines Tool安装(推荐)终端直接运行git命令根据流程安装先安装Command Lines Tool后再安装git 官网下载二进制文件进行安装官方国外源下载二进制文件(不推荐)国内镜像下载二进制文件(推荐)安装git 通过Xcode Command Lines Tool安装(推荐) 简单来讲C…...
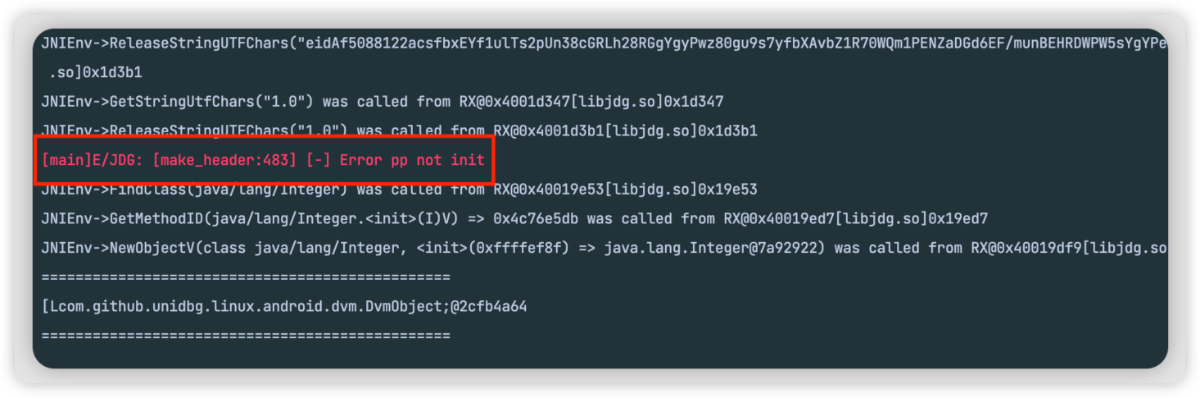
京东协议算法最新版
环境准备 1 com.jingdong.app.mall11.6.4 入口定位 逆向分析,发现 params 里面有一个 sign 以及请求头里面有一个 jdgs 首先我们发现京东的 sign 是 32 位的,猜测其可能是 md5 之类的 hash 算法,既然是 hash 算法,那么就大概率…...

软考系统架构设计师案例分析知识汇总
软件架构风格 △△△ 软件架构风格是描述某一类特定应用领域中软件系统组织方式和惯用方式。组织方式描述了系统的组成构件和这些构件的组织方式,惯用模式则反映众多系统共有的结构和语义。 面向对象架构风格的特征是将数据表示和基本操作封装在对象中。这种模式的构件是对象…...

MyBatis-plus 代码生成器
具体代码 application.yaml server:port: 8081 #自定义端口号spring:datasource:url: jdbc:mysql://localhost:3306/itcast?useUnicodetrue&characterEncodingutf-8&serverTimezoneGMT%2B8username: rootpassword: 123456driver-class-name: com.mysql.cj.jdbc.Driver…...

运维常识——网络
内网,公网IP 内网IP为专网IP 因为网络资源(IP地址不够,所以引出来了内网IP和IPv6) 内网IP和公网IP之分是为了减缓IP地址不够使用的情况 一般设置代理服务器 设置两张网卡 一张对外一张对内 内部主机将数据转发到内网卡&#…...
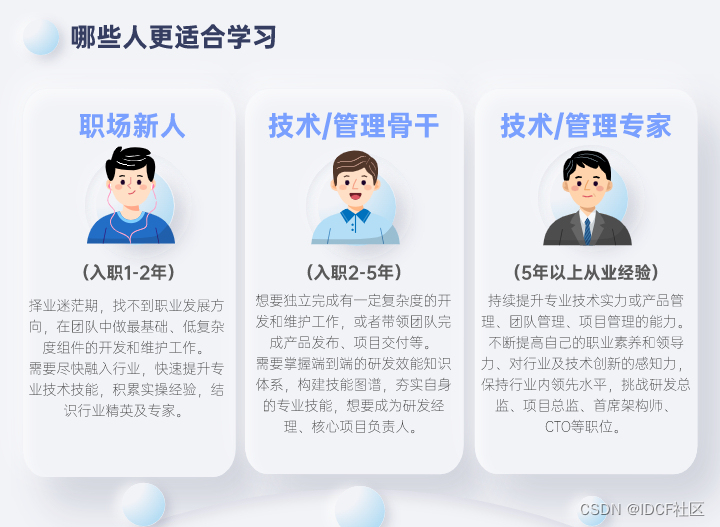
《研发效能(DevOps)工程师》课程简介(一)丨IDCF
为贯彻落实《关于深化人才发展体制机制改革的意见》,推动实施人才强国战略,促进专业技术人员提升职业素养、补充新知识新技能,实现人力资源深度开发,推动经济社会全面发展,根据《中华人民共和国劳动法》有关规定&#…...
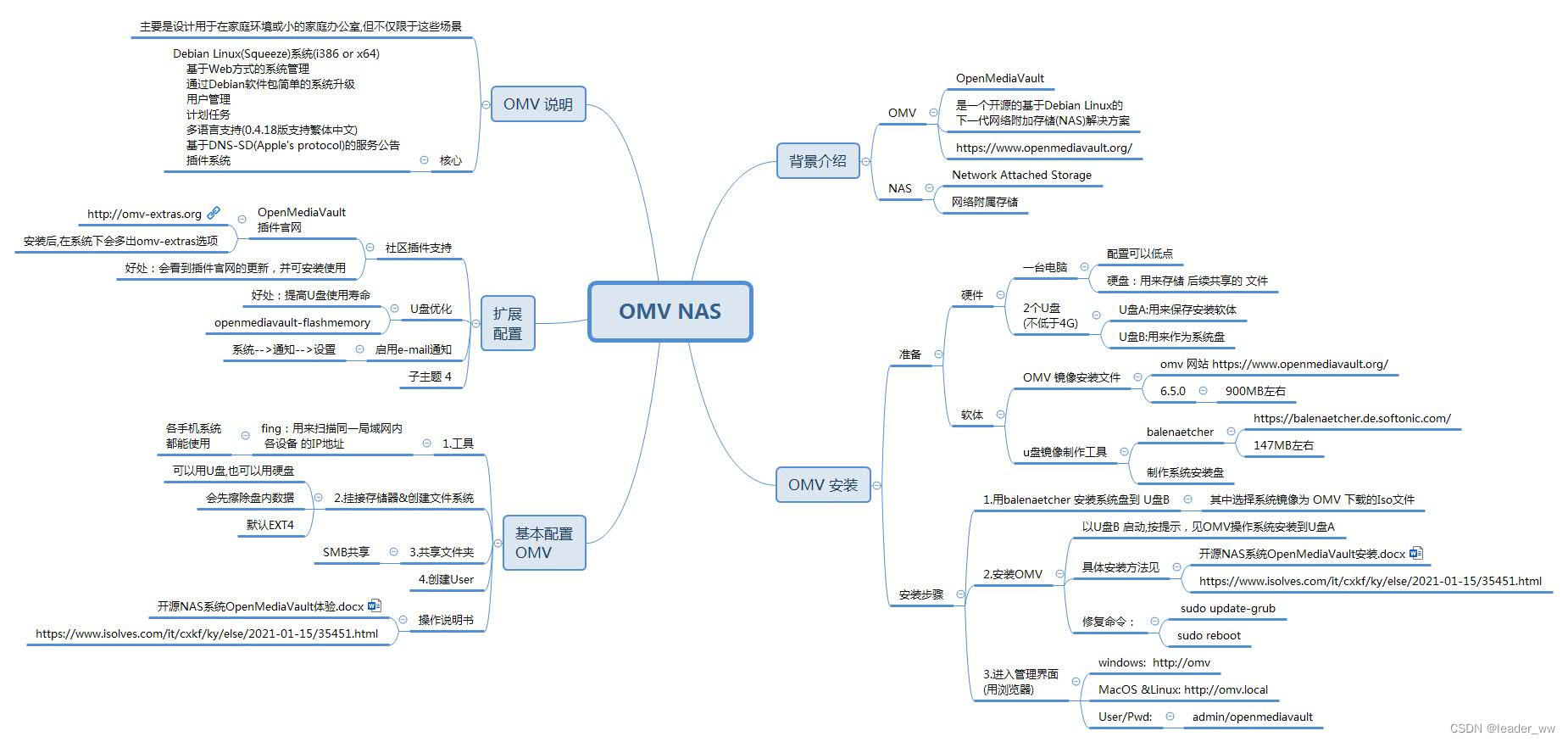
OMV 介绍及安装
# Time: 2023/11/02 #Author: Xiaohong # 运行电脑: Lenovo X201I (Intel(R) Core(TM) i3 CPU M 370 2.40GHz) # 功能: OMV 介绍及安装 导图 若OMV6 安装Extras 插件失败,可以参考 OMV6 安装Extras 插件失败的解决方法...
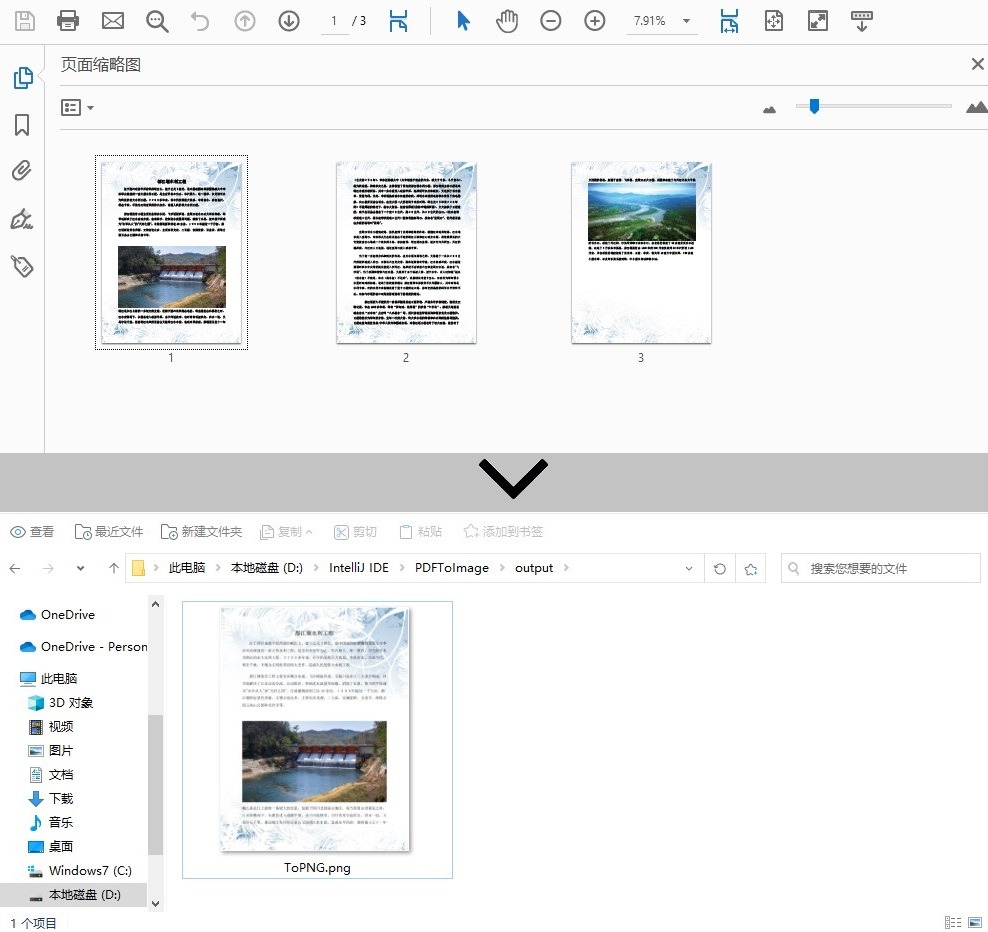
JAVA 实现PDF转图片(spire.pdf.free版)
1.引入jar包 导入方法1: 手动引入。将Free Spire.PDF for Java下载到本地,解压,找到lib文件夹下的Spire.PDF.jar文件。在IDEA中打开如下界面,将本地路径中的jar文件引入Java程序: 导入方法2:如果您想通过…...

高效学习工具之AnkiMobile新手入门指南(ios端,包括ipad、ihpone设备)————创建、使用、备份、设置参数、相关资料
文章目录 0 背景0.1 闭环学习0.2 什么是anki0.3 anki践行者经验分享 1 开始使用1.1 导入1.2 创建空白组1.3 创建卡片1.3.1 利用anki创建卡片的两种方法1.3.2 复习材料分类 1.4 筛选(做减法,拆分学习(做子卡牌集合))&am…...

LiveMeida视频接入网关
一、产品简介 视频接入网关主要部署在视频存储节点或视频汇聚节点,面向不同用户,主要用于对接不同厂家、不同型号的摄像机设备,获取摄像机视频后,以统一标准的视频格式和传输协议,将视频推送至上层联网/应用平台。可广…...

我和云栖有个约会
文章目录 云栖大会体验与感受大模型的体验感受 对大会的期待 云栖大会 云栖大会是是阿里巴巴集团主办的年度技术盛会,是云计算、大数据、人工智能等前沿技术产业发展的见证者、参与者和推动者。2023年的云栖大会于10月31日在杭州开幕,吸引了全球的技术专…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
