【OpenCV实现图像梯度,Canny边缘检测】
文章目录
- 概要
- 图像梯度
- Canny边缘检测
- 小结
概要
OpenCV中,可以使用各种函数实现图像梯度和Canny边缘检测,这些操作对于图像处理和分析非常重要。
图像梯度通常用于寻找图像中的边缘和轮廓。在OpenCV中,可以使用cv2.Sobel()函数计算图像的梯度,该函数可以计算图像在水平和垂直方向上的梯度。梯度的方向和大小可以帮助理解图像中的边缘信息。
Canny边缘检测是一种经典的边缘检测算法,它通过多个步骤来检测图像中的边缘。首先,Canny算法使用Sobel算子计算图像的梯度。然后,它通过非极大值抑制(Non-Maximum Suppression)来细化边缘。接着,Canny算法使用双阈值(Double Thresholding)来检测强边缘和弱边缘,并通过连接强边缘来得到最终的边缘图像。Canny边缘检测在图像处理中被广泛应用,因为它能够准确地检测出图像中的边缘。
在OpenCV中,可以使用cv2.Sobel()函数计算图像的梯度,而Canny边缘检测则可以通过cv2.Canny()函数实现。通过这些函数,可以方便地在OpenCV中实现图像梯度和Canny边缘检测,进而进行各种图像分析和处理任务。
图像梯度
寻找图像梯度,边缘等等。
函数:cv.Sobel(), cv.Scharr(), cvLaplacian() 等等。
Sobel和Scharr导数:
Sobel算子是一种结合了高斯平滑和微分操作的滤波器,因此它对图像中的噪声具有较好的抵抗能力。使用Sobel算子时,可以指定所需导数的方向,通过参数yorder和xorder来确定是垂直方向还是水平方向的导数。此外,还可以通过参数ksize指定核(kernel)的大小。当ksize设为-1时,OpenCV会使用3×3的Scharr滤波器,其结果通常比3×3的Sobel滤波器更为精确。
拉普拉斯导数
它计算了由关系式给出的图像的拉普拉斯算子,其中关系式为
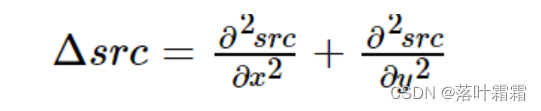
其中每一个导数都是用 Sobel 导数找到的。如果 ksize = -1,滤波器会使用下面这个内核。
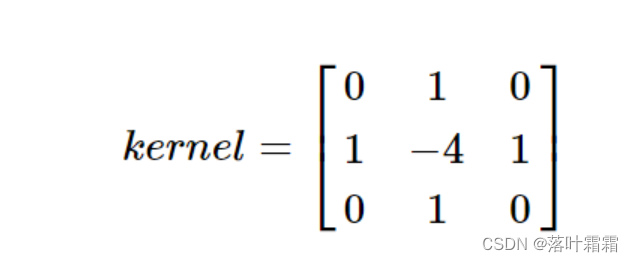
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt# 读取图像
img = cv.imread('dave.jpg', 0)# 计算拉普拉斯边缘
laplacian = cv.Laplacian(img, cv.CV_64F)# 计算Sobel边缘(x和y方向)
sobelx = cv.Sobel(img, cv.CV_64F, 1, 0, ksize=5)
sobely = cv.Sobel(img, cv.CV_64F, 0, 1, ksize=5)# 绘制原始图像
plt.subplot(2, 2, 1), plt.imshow(img, cmap='gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])# 绘制拉普拉斯边缘图像
plt.subplot(2, 2, 2), plt.imshow(laplacian, cmap='gray')
plt.title('Laplacian'), plt.xticks([]), plt.yticks([])# 绘制Sobel X边缘图像
plt.subplot(2, 2, 3), plt.imshow(sobelx, cmap='gray')
plt.title('Sobel X'), plt.xticks([]), plt.yticks([])# 绘制Sobel Y边缘图像
plt.subplot(2, 2, 4), plt.imshow(sobely, cmap='gray')
plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])# 显示图像
plt.show()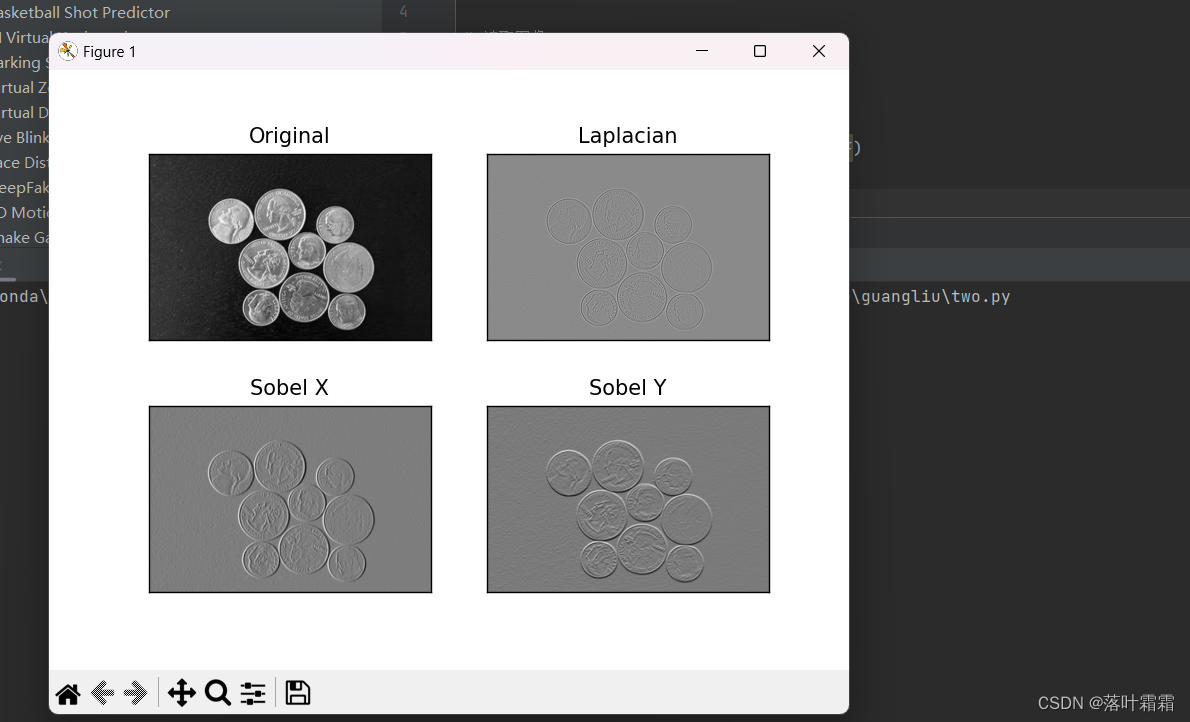
在我们的最后一个例子中,我们使用了Sobel滤波器来检测图像中的边缘。然而,当我们将输出数据类型转换为cv.CV_8U或者np.uint8时,存在一个小问题。在图像中,从黑色到白色的过渡被视为正斜率(它具有正值),而从白色到黑色的过渡被视为负斜率(它具有负值)。因此,当我们将数据类型转换为np.uint8时,所有负斜率都被截断为0,也就是说,我们会错过所有负斜率对应的边缘。
如果我们希望找到所有的边缘,更好的方法是将输出的数据类型保持在一个更高的精度范围内,例如cv.CV_16S、cv.CV_64F等,然后取其绝对值,最后再转换回cv.CV_8U类型。下面的代码演示了这个过程,特别是在处理水平Sobel滤波器时,以及结果的差异。
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt# 读取灰度图像
img = cv.imread('img.png', 0)# 使用Sobel滤波器,输出数据类型为cv.CV_8U
sobelx8u = cv.Sobel(img, cv.CV_8U, 1, 0, ksize=5)# 使用Sobel滤波器,输出数据类型为cv.CV_64F,然后取绝对值并转换为cv.CV_8U
sobelx64f = cv.Sobel(img, cv.CV_64F, 1, 0, ksize=5)
abs_sobel64f = np.absolute(sobelx64f)
sobel_8u = np.uint8(abs_sobel64f)# 显示原始图像、Sobel输出(cv.CV_8U)和Sobel绝对值(cv.CV_64F)
plt.subplot(1, 3, 1), plt.imshow(img, cmap='gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 3, 2), plt.imshow(sobelx8u, cmap='gray')
plt.title('Sobel CV_8U'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 3, 3), plt.imshow(sobel_8u, cmap='gray')
plt.title('Sobel abs(CV_64F)'), plt.xticks([]), plt.yticks([])# 显示图像
plt.show()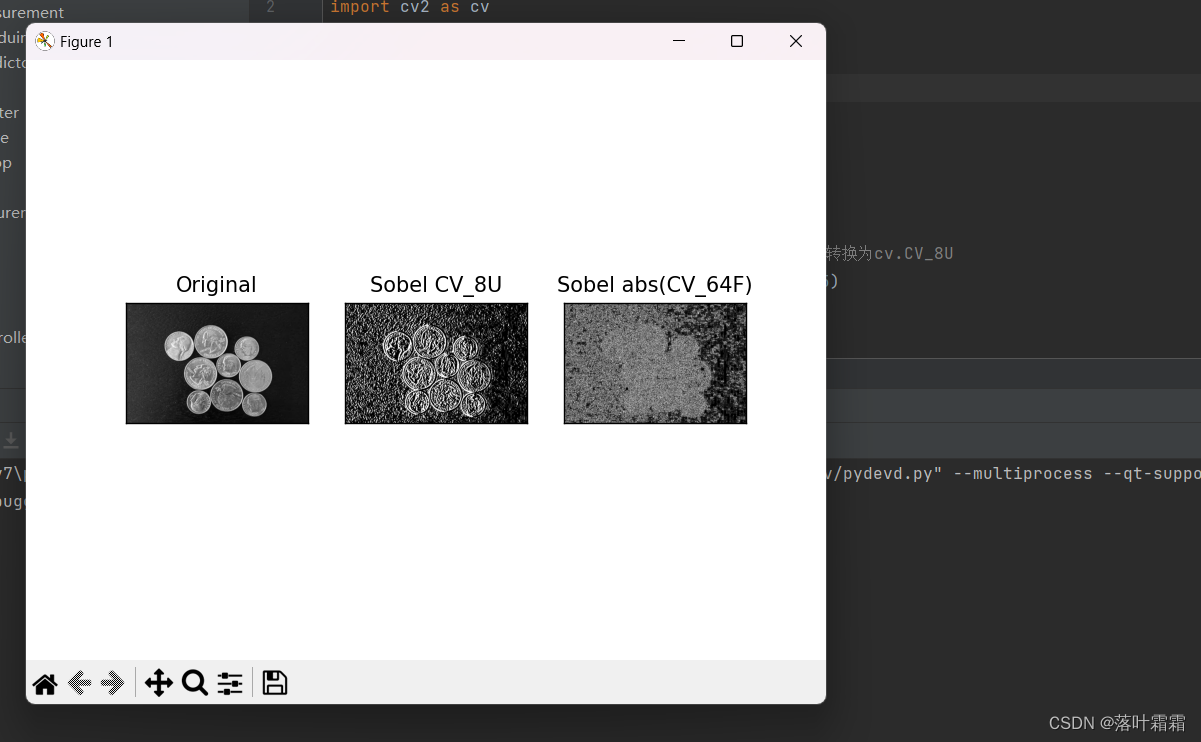
Canny边缘检测
Canny边缘检测的概念
OpenCV函数:cv.Canny()
Canny边缘检测是一种广泛应用的边缘检测算法,由John F. Canny开发而成。该算法包含多个阶段,下面我们将详细介绍每个阶段的过程:
噪声减少:
由于边缘检测对图像中的噪声非常敏感,第一步是通过一个5X5的高斯滤波器对图像进行平滑处理,以去除噪声。寻找图像中的变化(梯度)强度:
接下来,使用Sobel核在水平和垂直方向上对平滑后的图像进行滤波,得到水平方向($G_x$)和垂直方向($G_y$)的一阶导数。通过这两个导数,我们可以计算每个像素点的边缘梯度幅值和方向。梯度方向始终与边缘垂直,通常近似为水平、垂直和两个对角线方向中的一个。
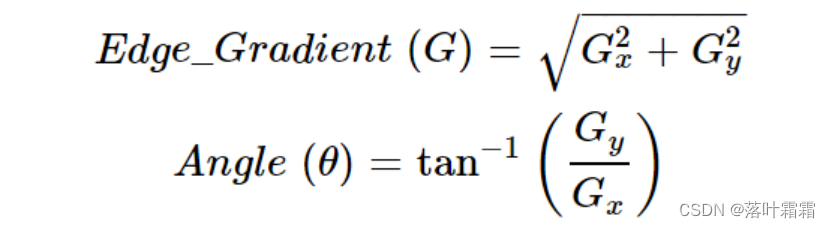
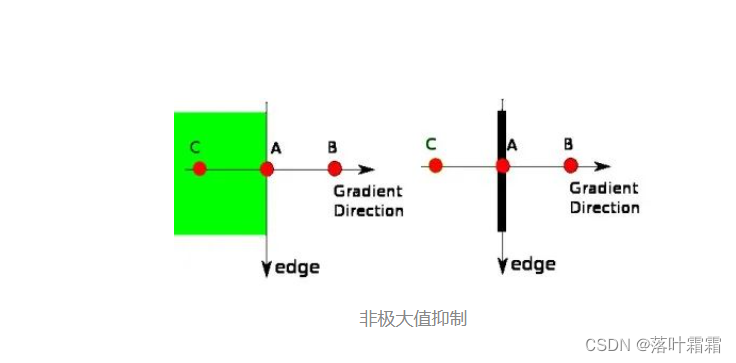
非极大值抑制:
在得到梯度大小和方向之后,在每个像素点上进行全图扫描。对于每个像素,检查其梯度值是否在相邻像素中是最大的。如果是,保留该值,否则将其置为0。这一步骤产生了一个"薄边"的二值图像。
滞后阈值:
在此阶段,我们需要确定哪些边缘是真实的,哪些是噪声或者假的。为此,我们使用两个阈值,minVal(最小值)和maxVal(最大值)。所有强度大于maxVal的边缘被视为真正的边缘,低于minVal的被丢弃。介于两者之间的边缘会基于连通性来判断是否为边缘。如果它们与确定的边缘相连,则保留,否则被抛弃。这一步骤也基于边缘是长线的假设来去除小的像素噪声。
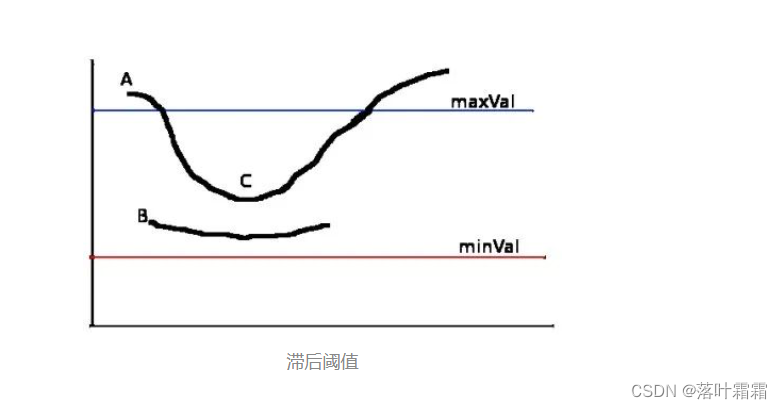
边缘 A 因为在 maxVal 上面,所以是肯定的边缘。尽管边缘 C 的位置在 maxVal 下面,但是因为它和边缘 A 相连接,所以我们认为它也是个有效边缘,如此得到了一条完整的曲线。但是对于边缘 B 来说,哪怕它在 minVal 上面,和边缘 C 处在同一个区域上,可是它并不和任何一条有效边缘连接,所以会被丢弃。所以,为了得到正确的结果,我们需要确定好 minVal 和 maxVal 的值。
最终,经过这些步骤,我们就能得到一条完整的边缘在图像中。
OpenCV中的Canny边缘检测
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt# 读取灰度图像
img = cv.imread('img.png', 0)# 使用Canny边缘检测算法,阈值设置为100和200
edges = cv.Canny(img, 100, 200)# 显示原始图像和Canny边缘检测结果
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])plt.subplot(122), plt.imshow(edges, cmap='gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([])plt.show()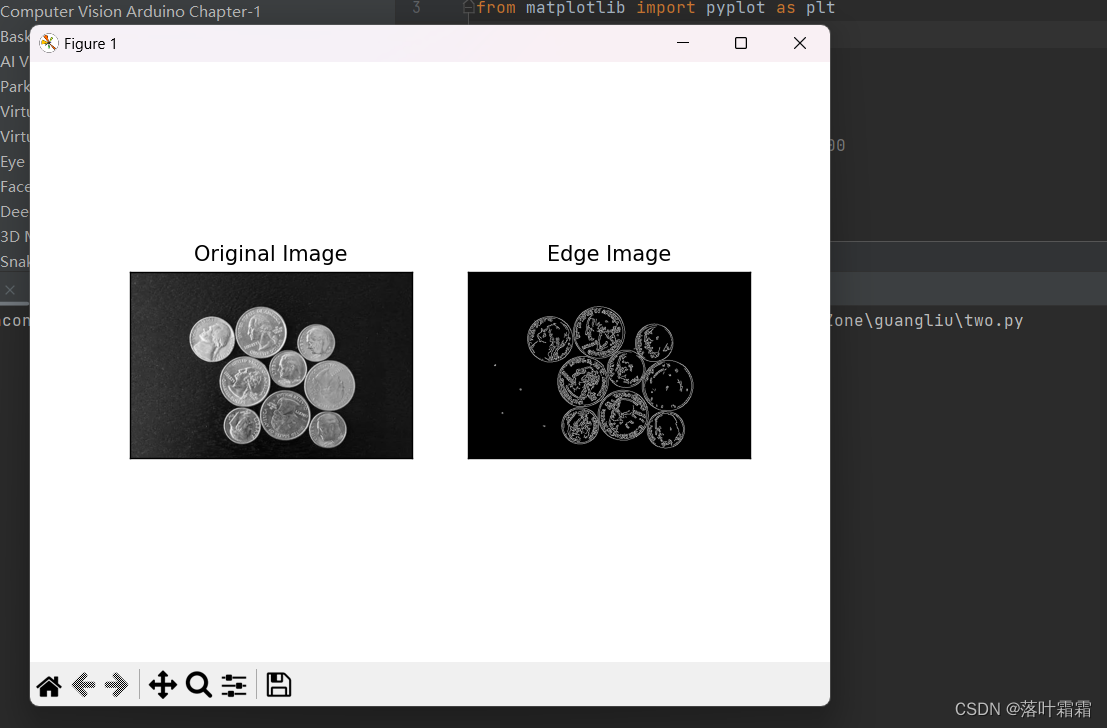
小结
图像梯度:
OpenCV提供了多种方法来计算图像的梯度,包括Sobel、Scharr和拉普拉斯滤波器。
Sobel算子是一种联合高斯平滑和微分操作的滤波器,可以计算图像在水平和垂直方向上的梯度。
使用Sobel算子时,你可以指定所需导数的方向(水平或垂直)以及核的大小。
拉普拉斯滤波器用于计算图像的拉普拉斯算子,通过将图像的二阶导数与Sobel导数相关联来实现。
Canny边缘检测:
Canny边缘检测是一种多阶段算法,用于检测图像中的边缘。
第一阶段是噪声减少,通常通过应用高斯滤波器来实现,以平滑图像并减少噪声。
第二阶段是计算图像的梯度,通常使用Sobel滤波器,以获得图像的水平和垂直梯度。
接下来进行非极大值抑制,以去除可能不构成边缘的像素,仅保留边缘像素。
最后一个阶段是滞后阈值,需要设置两个阈值(minVal和maxVal),以确定哪些边缘是真实的。根据这些阈值,边缘可能被分类为强边缘、弱边缘或非边缘,并进行相应的处理。
相关文章:

【OpenCV实现图像梯度,Canny边缘检测】
文章目录 概要图像梯度Canny边缘检测小结 概要 OpenCV中,可以使用各种函数实现图像梯度和Canny边缘检测,这些操作对于图像处理和分析非常重要。 图像梯度通常用于寻找图像中的边缘和轮廓。在OpenCV中,可以使用cv2.Sobel()函数计算图像的梯度…...

Spring Boot 解决跨域问题的 5种方案
跨域问题本质是浏览器的一种保护机制,它的初衷是为了保证用户的安全,防止恶意网站窃取数据。 一、跨域三种情况 在请求时,如果出现了以下情况中的任意一种,那么它就是跨域请求: 协议不同,如 http 和 https…...

linux 3.13版本nvme驱动阅读记录一
内核版本较低的nvme驱动代码不多,而且使用的是单队列的架构,阅读起来会轻松一点。 这个版本涉及到的nvme驱动源码文件一共就4个,两个nvme.h文件,分别在include/linux ,include/uapi/linux目录下,nvme-core.c是主要源码…...

掌握RESTful API:规范与设计详解
前言 RAML (RESTful API Modeling Language) 和 OAS (OpenAPI Specification) 都是用于描述和定义 RESTful API 的规范。它们分别提供了不同的功能和优势。 RAML(RESTful API Modeling Language): RAML简介 RAML(RESTful API M…...
「更新」Topaz Video AI v4.0.3中文版
Topaz Video AI是一款功能强大的视频处理软件,它利用人工智能技术对视频进行智能分析和优化,旨在为用户提供高效、智能的视频编辑和增强功能。 首先,Topaz Video AI具备强大的视频修复功能。它可以自动识别并修复视频中的各种问题࿰…...

OpenAI最新官方GPT最佳实践指南,一文讲清ChatGPT的Prompt玩法
原文:Sina Visitor System OpenAI的官网发表万字GPT最佳实践指南,讲清Prompt提示词的原则和策略,这里是总结和全文翻译 原创图像,AI辅助生成 OpenAI的官网上刚刚发表一篇万字的GPT最佳实践指南,这份指南把写好Promp…...
树结构及其算法-用链表来实现二叉树
目录 树结构及其算法-用链表来实现二叉树 C代码 树结构及其算法-用链表来实现二叉树 以链表实现二叉树就是使用链表来存储二叉树,也就是运用动态分配内存和指针的方式来建立二叉树。 使用链表来表示二叉树的好处是节点的增加与删除操作相当容易,缺点…...
:在hostapd获取已关联的STA的MAC地址)
openwrt(三):在hostapd获取已关联的STA的MAC地址
在深度开发openwrt的hostapd模块的时候,有些功能的实现需要获取已关联的sta的mac地址,下面是相关的方法描述: 第一、在sta_info.c文件中,可以找到一个名为struct hostap_sta_info * hostapd_get_sta(struct hostapd_data *hapd, …...

为何袁世凯要把“元宵节”改为“上元节”?
网民把春节除夕日排除在法定假期之外的相关热议,在微博评论区部分已被关闭。官方学者的解释是:“回归传统。” 这就令人难免要回顾历史,并发觉只有在袁世凯称帝之后,才有过取消“元宵节”改为“上元节”的笑话,因为“元…...
python将图片序列保存成gif
这里用到的模块是imageio。用imageio.mimsave即可将图片序列保存成gif动态图。以下是本人编写的小实验: import cv2 import imageiopaths ["./images/0001.png", "./images/0002.png", "./images/0003.png", ...] frames [] for i…...

UE4用C++修改蓝图对象的属性值
if (auto Property FindFProperty<FStrProperty>(Class, "A")){Object->Modify();Property->SetPropertyValue_InContainer(Object.GetClass(), "OK");}...

供应商等级:一级、二级和三级供应商之间有什么区别
作为一名专业采购人员,你知道拥有一个可靠且具有成本效益的供应链有多么重要。确保供应链顺利运行的方法之一就是利用供应商分级。 什么是供应商分级? 供应商分级是根据供应商的绩效和对企业的重要性,对其进行分类的做法。 因此,…...
)
软考 系统架构设计师系列知识点之净室软件工程(3)
接前一篇文章:软考 系统架构设计师系列知识点之净室软件工程(2) 所属章节: 第5章. 软件工程基础知识 第5节. 净室软件工程 相关试题 1. 以下关于软件开发方法的叙述,错误的是()。 A. 对于较为…...

『VUE H5页面 - PDF预览』
使用依赖:vue-pdf实现需求:将 PDF url 地址 转换为本地页面预览 <template><div class"pdf-preview"><NavBar /><div class"container"><VuePdf v-for"i in numPages" :key"i" cla…...

使用lua-resty-request库编写爬虫IP实现数据抓取
目录 一、lua-resty-request库介绍 二、使用lua-resty-request库进行IP数据抓取 1、获取IP地址 2、设置请求 3、处理数据 三、代码实现 四、注意事项 五、总结 本文将深入探讨如何使用lua-resty-request库在爬虫程序中实现IP数据抓取。我们将首先介绍lua-resty-request…...
vue-admin-templete项目配置在手机上预览
参考文档: https://blog.csdn.net/qq_29752857/article/details/109802801想要在手机上预览本地打开的vue-admin-templete项目,首先要确保手机和电脑在同一网段。 参考文档:https://blog.csdn.net/m0_57236802/article/details/1315234471.查…...
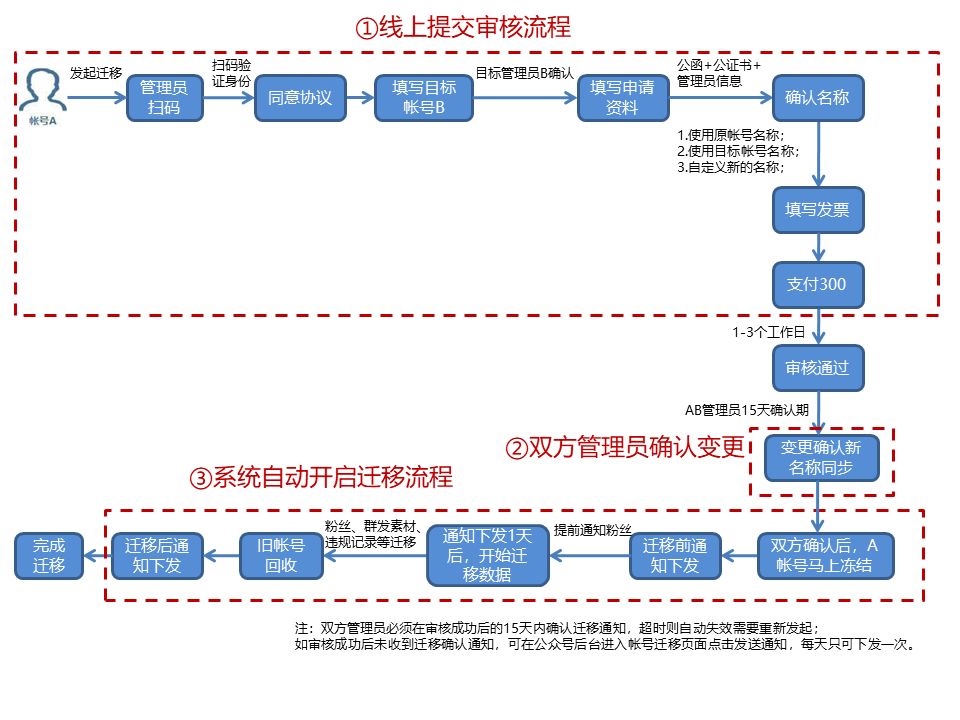
服务号升级订阅号的流程
服务号和订阅号有什么区别?服务号转为订阅号有哪些作用?首先我们要知道服务号和订阅号有什么区别。服务号侧重于对用户进行服务,每月可推送4次,每次最多8篇文章,发送的消息直接显示在好友列表中。订阅号更侧重于信息传…...

redhat7.4 安装lnmp操作环境
PacVim安装 https://baijiahao.baidu.com/s?id1601033830453371540&wfrspider&forpc 安装php https://www.cnblogs.com/alliancehacker/p/12255445.html https://blog.csdn.net/weixin_39709920/article/details/104274545 安装mysql https://www.cnblogs.com/laumian…...

Java判断是否有特殊字符串
//特殊字符串过滤private static String REGEX_RULE "[ _~!#$%^&*()|{}:;,\\[\\].<>/?~!#¥%……&*()——|{}【】‘;:\"”“’。,、?]|\n|\r|\t";pri…...
服务器搭建:从零开始创建自己的Spring Boot应用【含登录、注册功能】
当然,你可以先按照IDEA搭建SSM框架【配置类、新手向】完成基础框架的搭建 步骤 1:设计并实现服务器端的用户数据库 在这个示例中,我们将使用MySQL数据库。首先,你需要安装MySQL并创建一个数据库以存储用户信息。以下是一些基本步…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...
