数据结构入门5-2(数和二叉树)
目录
注:
树的存储结构
1. 双亲表示法
2. 孩子表示法
3. 重要:孩子兄弟法(二叉树表示法)
森林与二叉树的转换
树和森林的遍历
1. 树的遍历
2. 森林的遍历
哈夫曼树及其应用
基本概念
哈夫曼树的构造算法
1. 构造过程
2. 算法实现
哈夫曼编码
算法实现
文件的编码和译码
二叉树的运用 - 利用二叉树求解表达式
中缀表达式树的创建
中缀表达式树的求值
注:
本笔记参考:《数据结构(C语言版)》
接下来是树的表示、遍历操作及树林与二叉树之间的对应关系。
树的存储结构
1. 双亲表示法
用一组连续的存储单元存储树的结点,每个结点包括两个域:
![]()
例如:

- 优点:求结点的双亲和树的根会十分方便;
- 缺点:求结点的孩子时需要遍历整个结构。
------
2. 孩子表示法
由于每个结点可以有多棵子树,所以每个结点可以有多个指针域,每个指针域分别指向其中一棵子树的根结点:
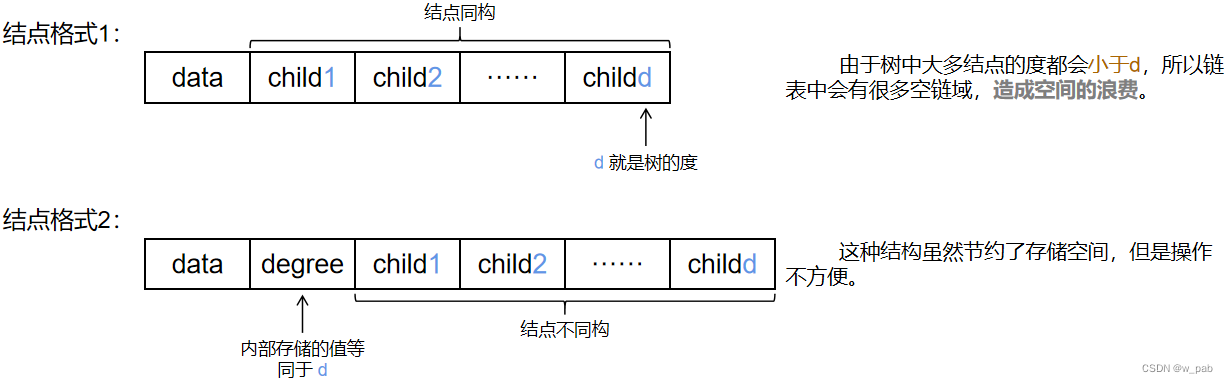
除此之外,还有一种存储结构:在这种存储结构中,由孩子结点组成了一个个线性表,并且把这些链表的头结点再组成一个线性表。
【例如】
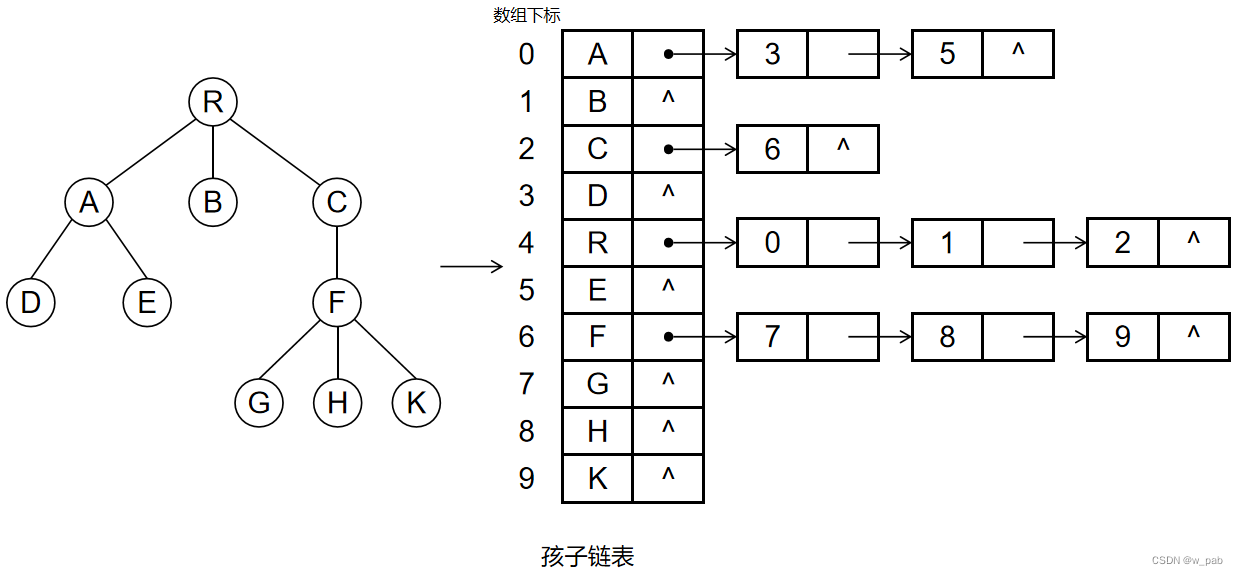
而如果把双亲表示法和孩子表示法结合起来,就会得到又一种存储结构:
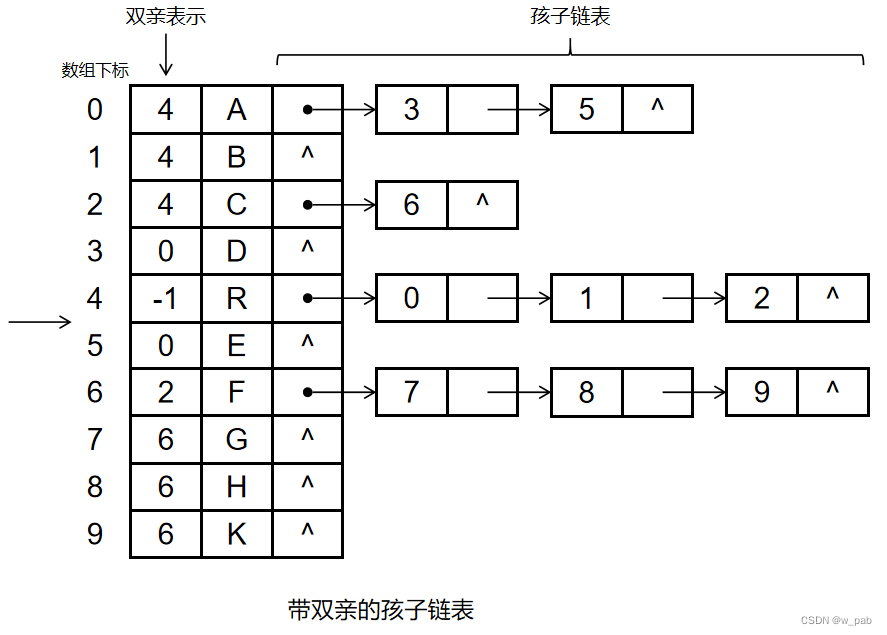
------
3. 重要:孩子兄弟法(二叉树表示法)
即将二叉链表作为树的存储结构,这种链表有两个链域:
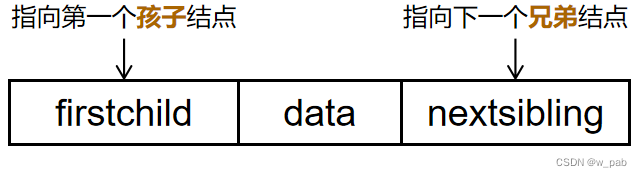
typedef struct CSNode {ElemType data;CSNode* firstchild, * nextsibling;
}CSNode, *CSTree;这种存储结构便于各种关于树的操作,譬如访问孩子节点:只需交替寻找 firstchild域 和 nextsibling域 即可。

而如果要方便寻找双亲结点,仅需在结构上多设置一个 parent域 即可。
如上图所示,这种存储结构与二叉链表完全一致,可以通过这种结构,将一般的树转换成二叉树进行处理。因此,孩子兄弟表示法的运用较为普遍。
森林与二叉树的转换
由上述的孩子兄弟表示法可知,任何一棵和树对应的二叉树,其根结点的右子树必空。例如:
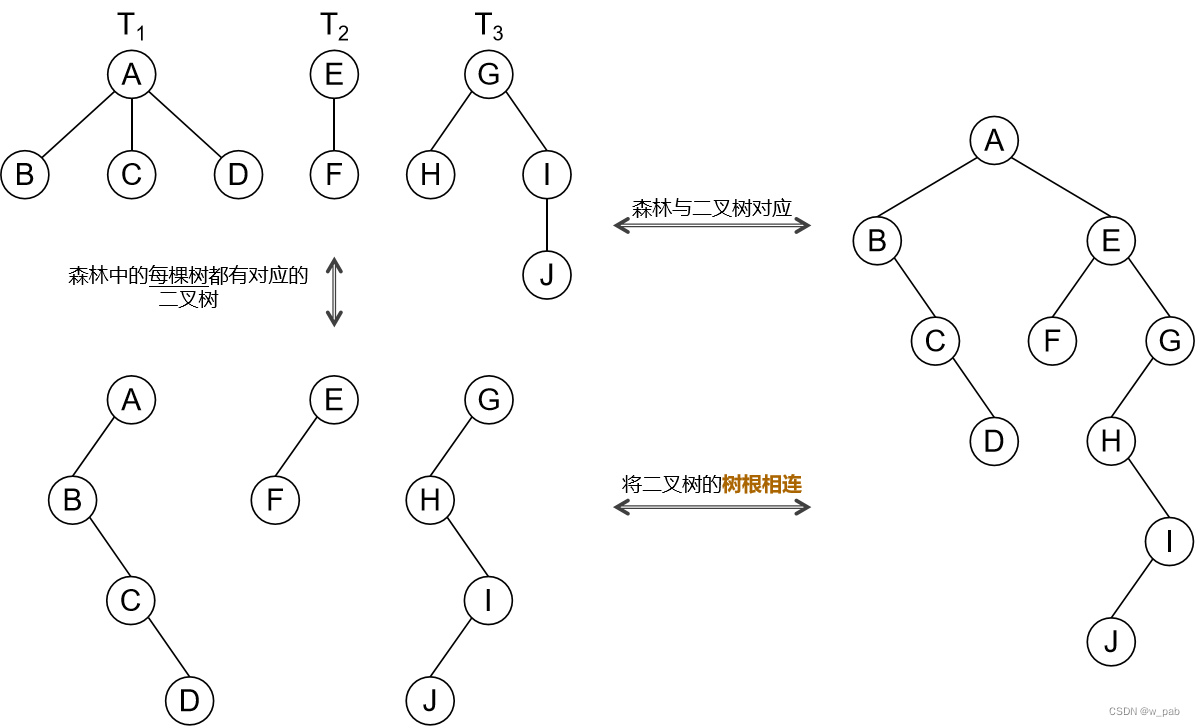
通过上述的例子,就可以揭示森林与二叉树之间的转换规律。
现在假设:
![]()
因为空树就是空二叉树,所以这种情况不做说明。
1. 森林转换为二叉树

2. 二叉树转换为森林

上述所描述的转换方式都可以通过递归实现。
树和森林的遍历
1. 树的遍历
与二叉树不同,树的遍历只有两种方式:
- 先根(次序)遍历:优先访问树的根结点,然后依此访问子树;
- 后根(次序)遍历:先后根遍历子树,再访问对应根结点。
【例如】
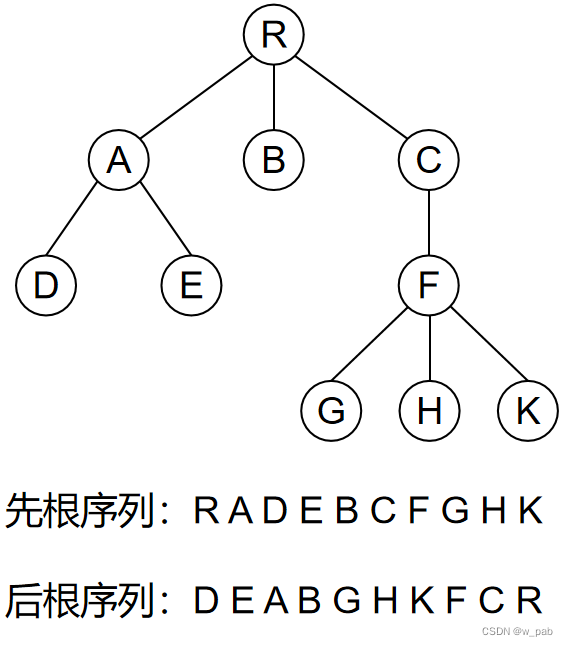
2. 森林的遍历
||| 森林和树之间是可以进行相互递归的。
遍历的一个前提:森林非空。
(1)先序遍历规则:
- 访问森林中第一棵树的根结点;
- 先序访问第一棵树的根结点的子树森林;
- 先序遍历由剩余的树构成的森林。
(2)中序遍历规则:
- 中序遍历森林中第一棵树的根结点的子树森林;
- 访问第一棵树的根结点;
- 中序遍历由剩余的树构成的森林。
【例如】
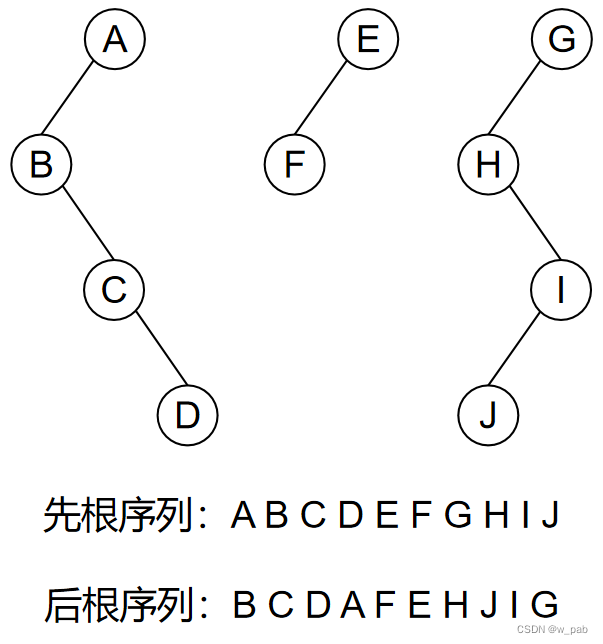
注:此处森林的先序和中序遍历,分别与对应二叉树的先序和中序遍历相对。
哈夫曼树及其应用
基本概念
||| 哈夫曼树(即最优二叉树):是一类带权路径长度最短的二叉树。
以下是一些会用到的概念:
| 概念 | 定义 |
| 路径 | 从树中的一个结点到另一个结点之间的 分支 构成两结点之间的路径 |
| 路径长度 | 即路径上的分支数目 |
| 树的路径长度 | 从树根到每一结点的路径长度之和 |
| 权 | 赋予某个实体的一个量 (是对实体的某个或某些属性的数值化描述) |
| 结点的带权路径长度 | = 该结点到树根之间的路径长度 × 结点上的权 |
| 树的带权路径长度(WSL) | = 树中 所有叶子结点 的带权路径长度之和 |
【例如】
有4个叶子结点a、b、c、d,分别带权7、5、2、4,这4个叶子结点存在于不同的二叉树上:
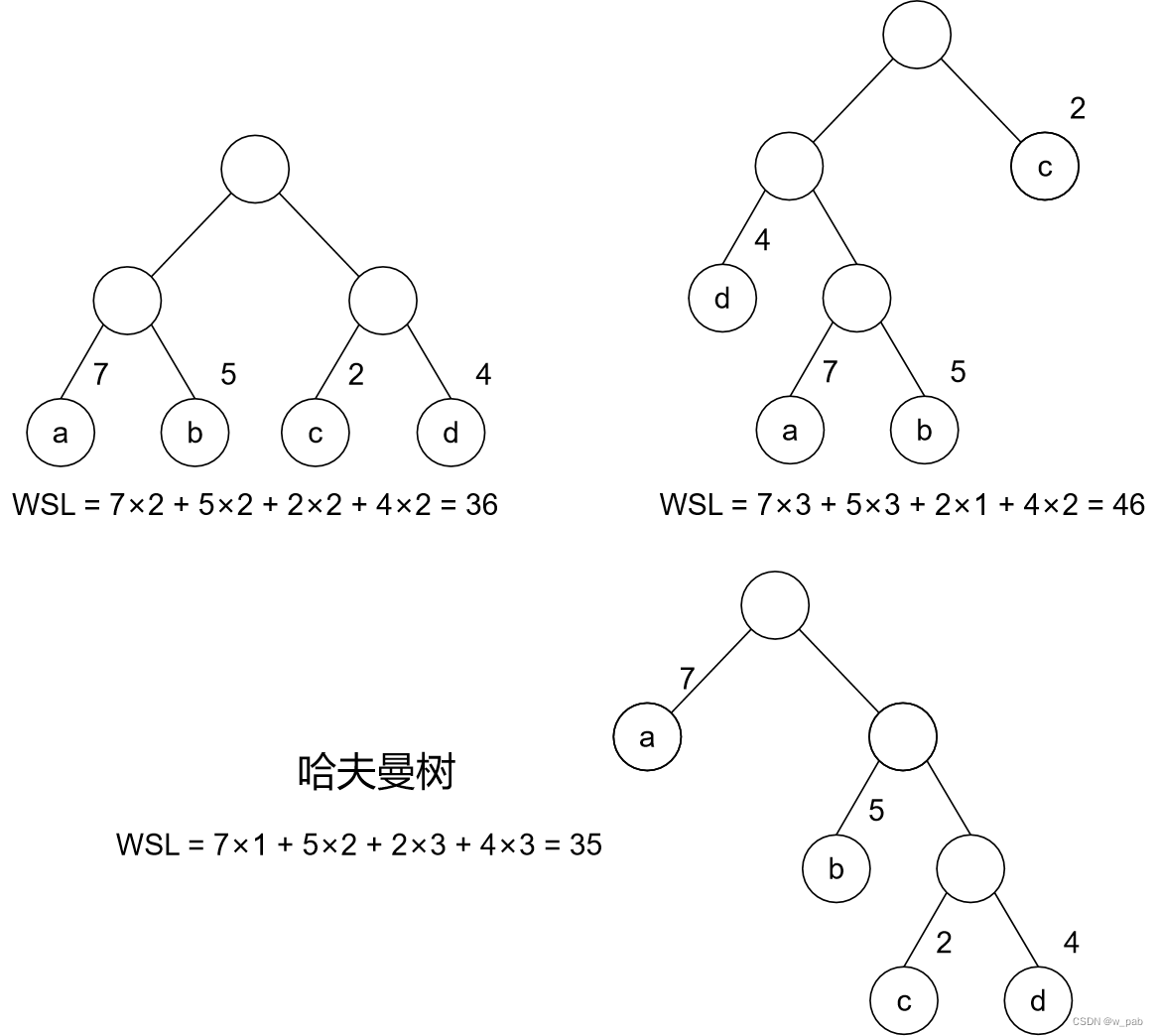
可以验证,下面的这棵树的带权路径长度恰好是最小的(或者说,在所有带权为7、5、2、4的4个叶子结点的二叉树中其值最小),它就是哈夫曼树。
由上述例子可以看出:在哈夫曼树中,权值越大的结点离根结点越近。
哈夫曼树的构造算法
1. 构造过程
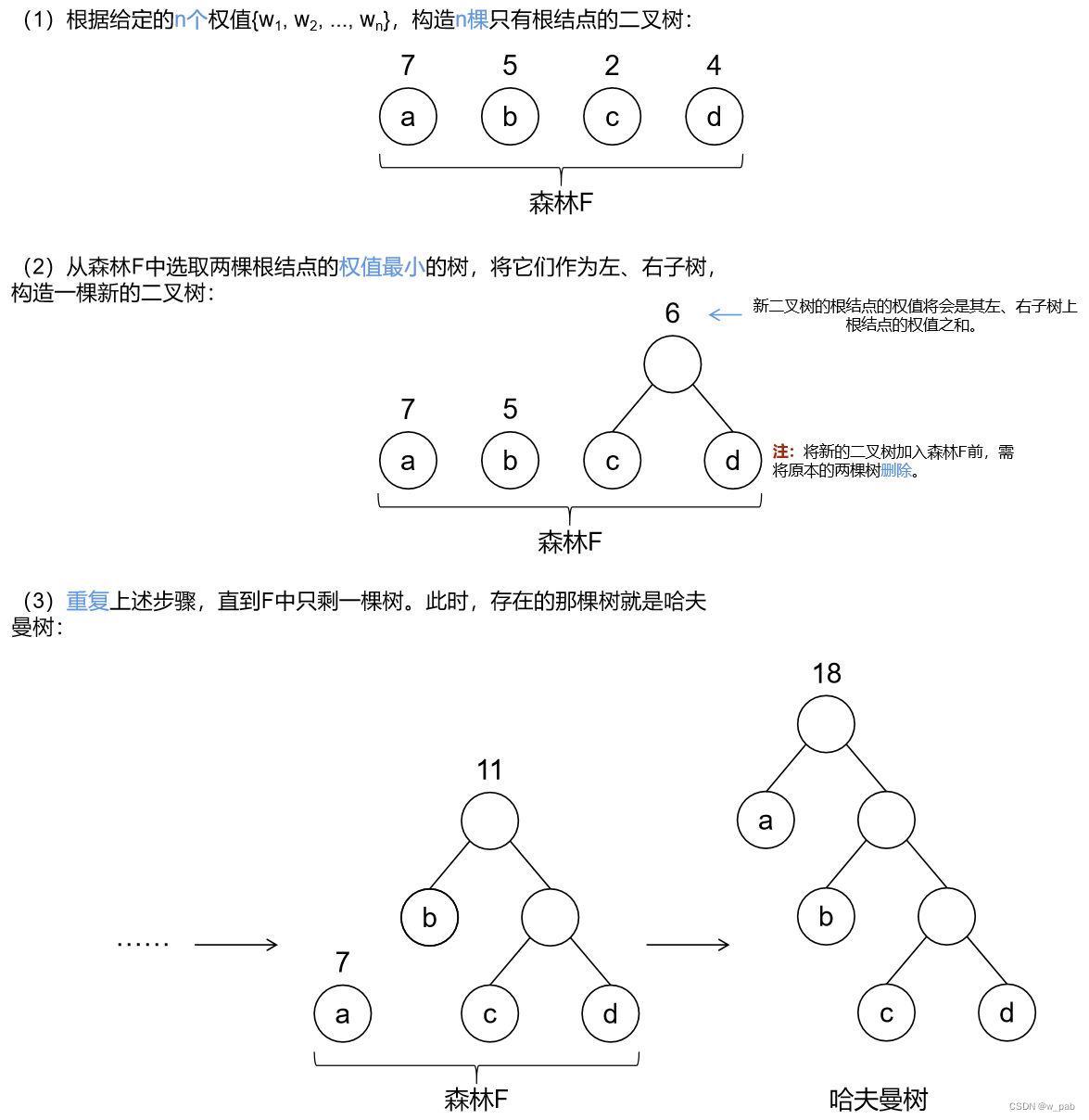
2. 算法实现
由上述构造可知,哈夫曼树中不存在度为1的结点。故若哈夫曼树存在n个叶子结点,则其总结点数一定是2n - 1。
哈夫曼树的结点存储结构:

若将上述的存储结构转换为代码,就是:
typedef struct
{int weight; //结点的权值int parent, lchild, rchild; //结点的双亲、左孩子和右孩子的下标
}HTNode, *HuffmanTree;注意:和以往的链式存储不同,此次是通过动态分配的方式对哈夫曼树进行存储。
在具体的实现中,为了方便,往往会将下标为0的单元置空,所以开辟的数组大小将会是2n。对存储内容进行分类:
- 前1~n个单元:存储叶子结点;
- 后n - 1个单元:存储非叶子结点。
【参考代码:构造哈夫曼树】
void CreateHuffmanTree(HuffmanTree& HT, int n)
{//---初始化开始---if (n <= 1)return;int m = 2 * n - 1;HT = new HTNode[m + 1]; //规定:HT[m]表示根结点for (int i = 1; i <= m; i++){ //处理 1 至 m 个单元(初始化)HT[i].parent = 0;HT[i].lchild = 0;HT[i].rchild = 0;}for (int i = 1; i <= n; i++){ //输入叶子结点的权值(即前n个结点)cin >> HT[i].weight;}//---初始化完毕,开始创建哈夫曼树---for (int i = n + 1; i <= m; i++){ //进行n-1次的构造操作int s1 = 0;int s2 = 0;SelectLeaves(HT, i - 1, s1, s2);//挑选目标结点HT[s1].parent = i; //更改双亲域(相当于删除s1和s2,得到了新结点i)HT[s2].parent = i;HT[i].lchild = s1; //将s1和s2作为i的孩子HT[i].rchild = s2;HT[i].weight = HT[s1].weight + HT[s2].weight;}
}
其中,函数SelectLeaves的参考如下(仅供参考):
//挑选要求: //1. 双亲域为0; //2. 权值最小。 void SelectLeaves(HuffmanTree HT, int i, int& s1, int& s2) {int left = 1;int right = i;while (left < right){if (HT[left].parent == 0 && HT[right].parent == 0){if (HT[left].weight <= HT[right].weight)right--;elseleft++;}else if (HT[left].parent != 0)left++;elseright--;}s1 = left;HT[s1].parent = 1;left = 1;right = i;while (left < right){if (HT[left].parent == 0 && HT[right].parent == 0){if (HT[left].weight <= HT[right].weight)right--;elseleft++;}else if (HT[left].parent != 0)left++;elseright--;}s2 = left; }
哈夫曼编码
为了对数据文件进行尽可能的压缩,有人提出了不定长编码的概念:为出现次数较多的字符编以较短的代码。而通过哈夫曼树设计的二进制编码,就可以满足这一需求。

在上图中,约定:
- 左分支标记为0;
- 右分支标记为1。
由此,根结点到每个叶子结点的路径上的0、1序列就构成了相应字符的编码。这种由各分支的赋值构成的二进制串,就是哈夫曼编码。
前缀编码的概念(提及):若在一个编码方案中,任一编码都不是其他任何编码的前缀(最左子串),则称该编码为前缀编码。譬如:
前缀编码: 0, 10, 110, 111
非前缀编码:0, 01, 010, 111
哈夫曼编码的两个性质:
- 哈夫曼编码是前缀编码(因为路径的不同);
- 哈夫曼编码是最优前缀编码:对于包含n个字符的数据文件,分别以字符的出现次数为权值构造哈夫曼树,再用该树对应的哈夫曼编码压缩文件,可使文件压缩后对应的二进制文件长度最短。
算法实现
主要思想:
- 从叶子出发,向上回溯至根结点。
- 回溯时,走左分支则生成代码0。
- 回溯时,走右分支则生成代码1。
使用一个指针数组作为哈夫曼编码表,存放每个字符编码串的首地址(依旧是从1号单元开始使用):
typedef char** HuffmanCode; //通过动态分配数组存储哈夫曼表在动态开辟数组时,会发现:由于当前并不清楚每个字符编码的长度,所以不能为每个字符分配合适的存储空间。为了解决这个麻烦,通常会动态分配一个长度为n的一维数组作为临时的存储。
注意:由于求解编码的过程是向上回溯的,所以对于每个字符,得到的编码顺序是从右往左的。因此,在将编码往临时的一维数组cd内存储时,顺序也是从后向前的(即字符的第一个编码应该存储到 cd[n - 2] 中,以此类推)。
【参考代码】
void CreateHuffmanCode(HuffmanTree HT, HuffmanCode& HC, int n)
{//将从叶子到根结点回溯求得的每个字符的哈夫曼编码,存储到编码表HC中HC = new char* [n + 1]; //分配存储n个字符编码的编码表空间char* cd = new char[n]; //分配临时存放每个字符编码的动态存储空间cd[n - 1] = '\0'; //编码结束符for (int i = 1; i <= n; i++) //逐字符求编码{int start = n - 1; //从后往前写入int c = i; //从每个叶子结点开始int f = HT[i].parent;while (f != 0) //直到回到根结点为止{--start;if (HT[f].lchild == c) //左、右分支对应不同的代码cd[start] = '0';elsecd[start] = '1';c = f; //继续回溯f = HT[f].parent;}HC[i] = new char[n - start]; //分配空间strcpy(HC[i], &cd[start]); //将求得的编码复制到HC中}delete[] cd;
}【例子】
设在一系统通信内只可能出现8种字符,出现概率分别为0.05,0.29,0.07,0.08,0.14,0.23,0.03,0.11。
为设计哈夫曼编码,将概率作为对应字符的权值,得到:w = (5, 29, 7, 8, 14, 23, 3, 11)。其对应的哈夫曼表为:
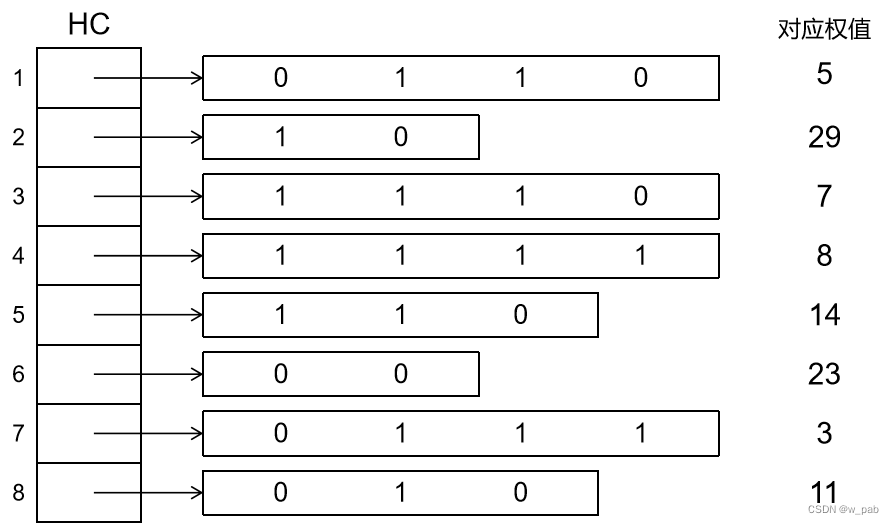
文件的编码和译码
在完成字符集的哈夫曼编码表后,就可以进行编码和译码的操作。
对数据文件进行编码的过程是:
- 依此读入文件中的字符;
- 在哈夫曼编码表HC中找到此字符;
- 将对应字符转换为编码表中存放的编码串。
对编码后的文件进行译码的过程是:
- 依此读入文件中的二进制码;
- 从哈夫曼树的根结点(即HT[m])出发,读入0,则进左孩子;读入1,则进右孩子。一旦到达某一叶子HT[i],则译出相应的字符编码HC[i];
- 循环上述步骤,直到文件结束。
二叉树的运用 - 利用二叉树求解表达式
对于任一算术表达式,都可以使用二叉树进行表示。而当对应二叉树创建完毕时,就可以利用对于二叉树的操作,进行表达式的求值运算。
中缀表达式树的创建
假设:运算符均为双目运算符。
由于创建的表达式树需要准确表达运算的次序,所以需要考虑各个运算符之间的优先级。为此,可以借助一个运算符栈,来存储未处理的运算符。
由两个操作数与一个运算符即可建立一棵表达式二叉树,而该二叉树又可以是另一棵树的子树。可以结组一个表达式树栈,以此来暂存已建立好的树。
【参考代码】
假设每个表达式的开头和结尾均为“#”。
两个工作栈:
- OPTR,用来暂存运算符。
- EXPT,用来暂存已建立好的表达式树的根结点。
【参考代码】
BiTree InitExpTree()
{SqStack EXPT;LinkStack OPTR;InitStack(EXPT); //初始化栈InitLinkStack(OPTR);LinkPush(OPTR, '#'); //将表达式起始符‘#’压入栈顶char ch = 0;cin >> ch;while (ch != '#' || LinkGetTop(OPTR) != '#') //表达式未扫描完毕 || OPTR栈顶元素不是‘#’{if (!In(ch)) //ch不是运算符{BiTree T = new BiTNode;CreateExpTree(T, NULL, NULL, ch); //以ch为根创建一棵只有根结点的二叉树Push(EXPT, T); //将二叉树根结点T压入EXPT栈内cin >> ch;}else{switch (Precede(LinkGetTop(OPTR), ch)) //比较二者的优先级{case '<':{LinkPush(OPTR, ch); //当前字符入栈cin >> ch;break;}case '>':{char theta = 0;BiTree T = new BiTNode;BiTree a = new BiTNode;BiTree b = new BiTNode;LinkPop(OPTR, theta); //弹出OPTR栈顶的运算符Pop(EXPT, b); //弹出EXPT栈顶的两个运算数Pop(EXPT, a);CreateExpTree(T, a, b, theta); //创建新的子树Push(EXPT, T);break;}case '=': //仅当:OPTR栈顶元素是'(',字符ch是')'{char x = 0;LinkPop(OPTR, x);cin >> ch;break;}}}}BiTree T = new BiTNode;Pop(EXPT, T);return T;
}由于字符的限制,上述算法只能进行10以内的运算。
【算法分析】
- 时间复杂度:遍历表达式中的每个字符,故时间复杂度为O(n);
- 空间复杂度:算法运行时所占用的辅助空间主要有OPTR栈和EXPT栈,它们的大小之和不会超过n,故空间复杂度为O(n)。
中缀表达式树的求值
【参考代码】
int EvaluateExpTree(BiTree T)
{int lvalue = 0, rvalue = 0; ///初始值均为0if (T->rchild == NULL && T->lchild == NULL)return T->data - '0'; //若当前结点为操作数,则返回该结点的对应数值else //若结点为操作符{lvalue = EvaluateExpTree(T->lchild);rvalue = EvaluateExpTree(T->rchild);return GetValue(T->data, lvalue, rvalue); //对取得的两个操作数进行计算}
}其中,函数GetValue就是对加、减、乘、除四种运算进行处理的函数。
该算法的时间复杂度和空间复杂度均为O(n)。
相关文章:

数据结构入门5-2(数和二叉树)
目录 注: 树的存储结构 1. 双亲表示法 2. 孩子表示法 3. 重要:孩子兄弟法(二叉树表示法) 森林与二叉树的转换 树和森林的遍历 1. 树的遍历 2. 森林的遍历 哈夫曼树及其应用 基本概念 哈夫曼树的构造算法 1. 构造过程 …...

把Redis当作队列来用,到底合适吗?
文章目录 前言从最简单的开始:List 队列发布/订阅模型:Pub/Sub趋于成熟的队列:Stream1) Stream 是否支持「阻塞式」拉取消息?2) Stream 是否支持发布 / 订阅模式?3) 消息处理时异常,Stream 能否保证消息不丢失,重新消费?4) Stream 数据会写入到 RDB 和 AOF 做持久化吗?…...

Python学习-----项目设计1.0(设计思维和ATM环境搭建)
目录 前言: 项目开发流程 MVC设计模式 什么是MVC设计模式? ATM项目要求 ATM项目的环境搭建 前言: 我个人学习Python大概也有一个月了,在这一个月中我发布了许多关于Python的文章,建立了一个Python学习起步的专栏…...
python网络爬虫(理论+实战)——爬虫实战:指定关键词的百度新闻爬取)
(九)python网络爬虫(理论+实战)——爬虫实战:指定关键词的百度新闻爬取
系列文章目录 (1)python网络爬虫—快速入门(理论+实战)(一) (2)python网络爬虫—快速入门(理论+实战)(二) (3) python网络爬虫—快速入门(理论+实战)(三) (4)python网络爬虫—快速入门(理论+实战)(四) (5)...
数据分析面试、笔试题汇总+解析(六)
(接上篇) 面试题(MySQL篇) 3. 如何提高MySQL的查询速度? 考点解析: 考察面试者对MySQL查询优化的理解 参考答案: (因为这个问题如果回答的详细一点可以写上一整篇,…...

vue3+rust个人博客建站日记3-编写主页
内容 绘制了主页的基本布局设置了封装了header栏组件并设置了全局黑夜模式. 选择一个组件库-Naive UI 如果没有设计能力,又想开发出风格统一的前端页面。就一定要选择一个漂亮的组件库。 本次项目选择使用Naive UI,NaivUI库曾被Vue框架作者尤雨溪推荐…...
前端常考react面试题(持续更新中)
react diff 算法 我们知道React会维护两个虚拟DOM,那么是如何来比较,如何来判断,做出最优的解呢?这就用到了diff算法 diff算法的作用 计算出Virtual DOM中真正变化的部分,并只针对该部分进行原生DOM操作,而…...

C++11多线程编程 二:多线程通信,同步,锁
C11多线程编程 一:多线程概述 C11多线程编程 二:多线程通信,同步,锁 C11多线程编程 三:锁资源管理和条件变量 2.1 多线程的状态及其切换流程分析 线程状态说明: 初始化(Init)&am…...
js——原型和原型链
最近看了很多面试题,看到这个js原型是常考点,于是,我总结了一些该方面的知识点分享给大家,其实原型就是那么一回事,搞明白了就没啥了。结果如下图所示:原型原型又可分为显式原型和隐式原型1.1显式原型显式原…...
[计算机网络(第八版)]第三章 数据链路层(学习笔记)
物理层解决了相邻节点透明传输比特的问题 3.1 数据链路层的几个共同问题 3.1.1 数据链路和帧 链路: 从一个节点到相邻节点的一段物理线路,中间没有任何其他的交换节点 数据链路: 节点间的逻辑通道是把实现控制数据传输的协议的硬件和软件加…...

void在不同场景下的意义
指针一般有三种含义:一是指明数据的位置,体现在指针的值,表示一个地址。二是表示数据类型的大小,例如int指针表示四个字节为一组数据,体现在指针的加减法如何计算。三是表示数据如何被解释,例如float指针和…...

Flume简介
Flume是一个高可用,高可靠,分布式的海量日志采集、聚合和传输的系统,能够有效的收集、聚合、移动大量的日志数据。 优点: 使用Flume采集数据不需要写一行代码,注意是一行代码都不需要,只需要在配置文件中…...
java简单学习
Java 基础语法 一个 Java 程序可以认为是一系列对象的集合,而这些对象通过调用彼此的方法来协同工作。下面简要介绍下类、对象、方法和实例变量的概念。 对象:对象是类的一个实例,有状态和行为。例如,一条狗是一个对象ÿ…...
Vue2 组件基础使用、父子组件之间的传值
一、什么是组件如画红框的这些区域都是由vue里的各种组件组成、提高复用信通常一个应用会以一棵嵌套的组件树的形式来组织:例如,你可能会有页头、侧边栏、内容区等组件,每个组件又包含了其它的像导航链接、博文之类的组件。为了能在模板中使用…...

代码随想录算法训练营 || 贪心算法 122 55 45
Day28122.买卖股票的最佳时机II力扣题目链接给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。注意:你不能同时参与多笔交易…...
数据结构基础之栈和队列
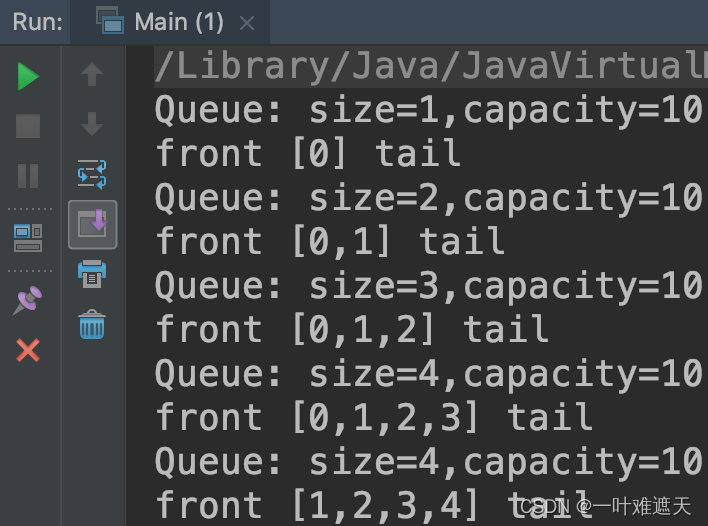
目录 前言 1、栈 2、队列 2.1、实现队列 2.2、循环队列 前言 上一篇中我们介绍了数据结构基础中的《动态数组》,本篇我们继续来学习两种基本的数据结构——栈和队列。 1、栈 特点:栈也是一种线性结构,相比数组ÿ…...
【Spark分布式内存计算框架——Spark Streaming】3.入门案例(上)官方案例运行
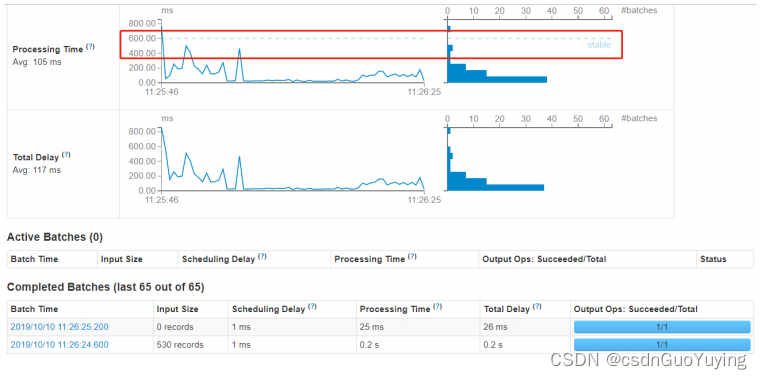
2.1 官方案例运行 运行官方提供案例,使用【$SPARK_HOME/bin/run-example】命令运行,效果如下: 具体步骤如下: 第一步、准备数据源启动端口,准备数据 nc -lk 9999 spark spark hive hadoop spark hive 第二步、运行…...

【博学谷学习记录】超强总结,用心分享 | 架构师 Tomcat源码学习总结
文章目录TomcatTomcat功能需求分析Tomcat两个非常重要的功能(身份)Tomcat的架构(设计实现)连接器的设计连接器架构分析核心功能ProtocolHandler 组件1.EndPoint组件EndPoint类结构图2.Processor组件Processor类结构图3.Adapter组件…...
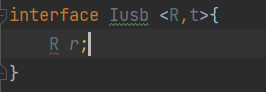
泛型<E>
泛型 案例引出泛型 按要求写出代码: 在ArrayList中添加3个Dog对象,Dog对象有name和age两个属性,且输出name和age public class test1 {public static void main(String[] args) {ArrayList list new ArrayList();list.add(new Dog(10,&quo…...

你对MANIFEST.MF这个文件知道多少?
前言我们在读源码过程中,经常看到每个jar包的METE-INF目录下有个MANIFEST.MF文件,这个文件到底是做什么的呢?在计算机领域中,"manifest" 通常指的是一份清单或概要文件,用于描述一组文件或资源的内容和属性。…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
