数据结构(超详细讲解!!)第二十节 数组
1.定义
1.概念
相同类型的数据元素的集合。
记作:A=(A0,A1,…,Am-1)
二维数组可看作是每个数据元素都是相同类型的一维数组的一维数组。多维数组依此类推。
二维数组是数据元素为线性表的线性表。

A=(A0,A1,……,An-1)
其中: Ai=(ai0,ai1,……,ai m-1) (0≤i≤n-1)
Am×n的二维数组

矩阵Am×n看成n个列向量的线性表
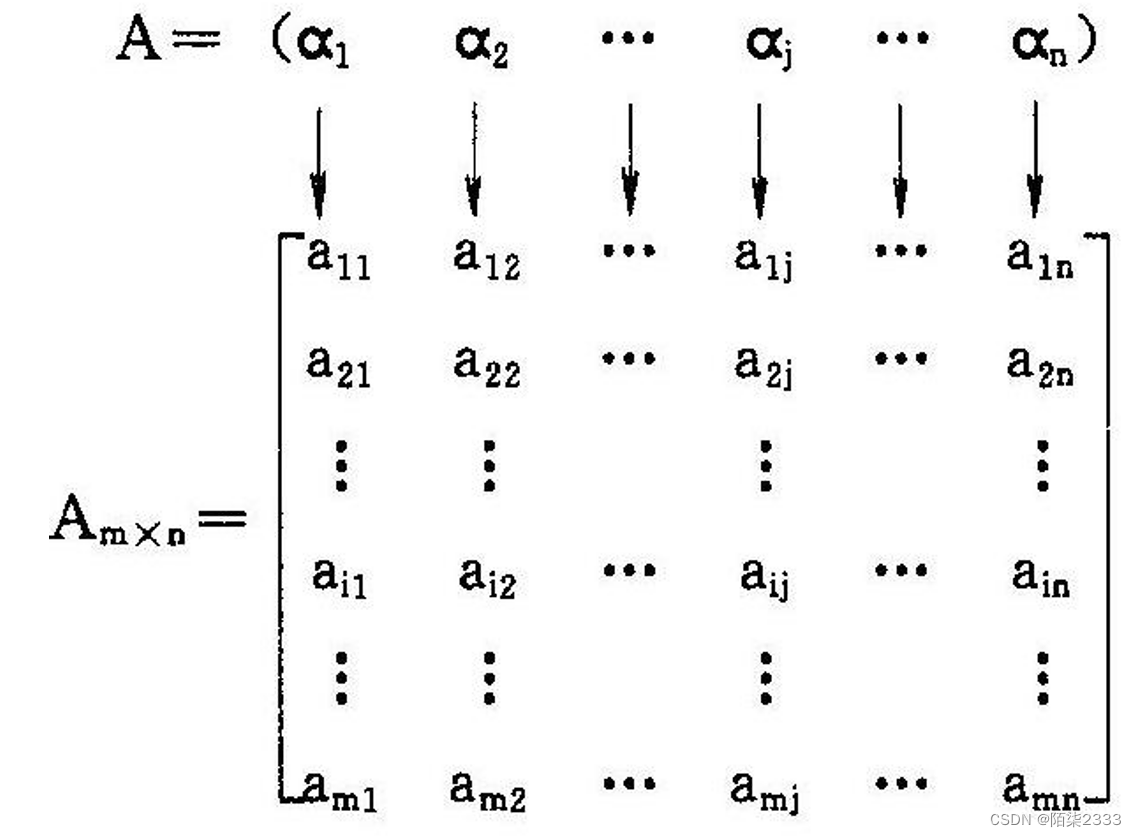
矩阵Am×n看成m个行向量的线性表

以上我们以二维数组为例介绍了数组的结构特性,实际上数组是一组有固定个数的元素的集合。
也就是说,一旦定义了数组的维数和每一维的上下限,数组中元素的个数就固定了。
例如二维数组A3×4,它有3行、4列,即由12个元素组成。
由于这个性质,使得对数组的操作不像对线性表的操作那样可以在表中任意一个合法的位置插入或删除一个元素。
对于数组的操作一般只有两类:
(1) 获得特定位置的元素值;
(2) 修改特定位置的元素值。
2.数组的逻辑结构定义
数组的逻辑结构定义:ARRAY=(D, R)
其中D是数据元素的集合,R是描述下标的关系的集合
由此,对于一维数组有:
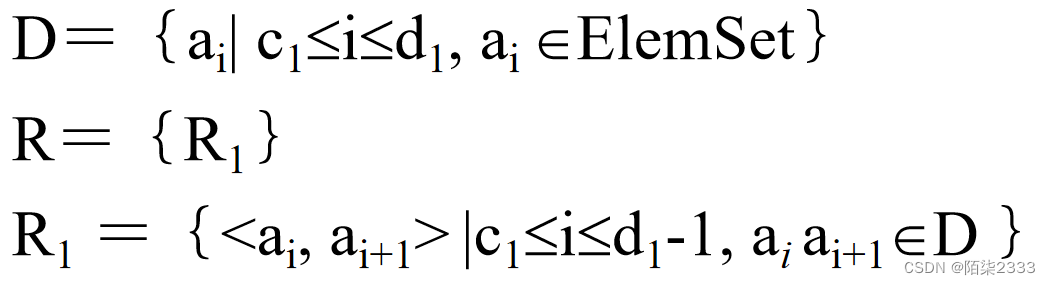
c1 ,d1为一维数组下标的下界和上界。
二维数组:
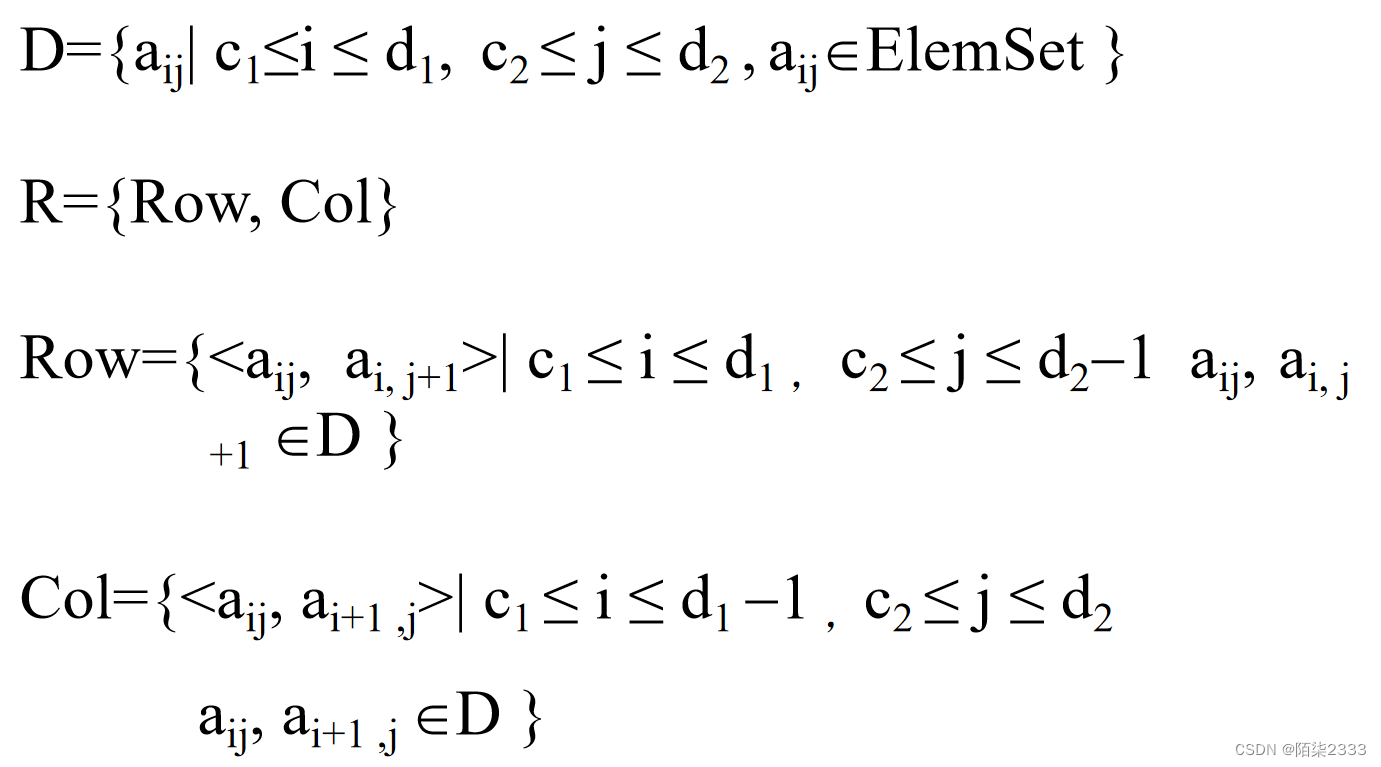
n维数组:

逻辑特性:

3.数组的抽象类型定义:

基本操作:
基本操作:InitArray(&A,n,bound1,…,boundn)操作结果:若维数n和各维长度合法,则构造相应的数组A,并返回OK。DestroyArray(&A)操作结果:销毁数组A。Value(A,&e,index1,…,indexn)初始条件:A 是n维数组,e为元素变量,随后是n个下标值。操作结果:若各下标不越界,则e赋值为所指定的A的元素值,并返回OK。Assign(&A,e,index1,…,indexn)初始条件:A是n维数组,e为元素变量,随后是n个下标值。操作结果:若下标不越界,则将e的值赋值给所指定的A的元素,并返回OK。
}//ADT Array
2.数组的顺序表示和实现
由于数组的运算一般不包括插入和删除,因此不必考虑数据元素的移动。因而采用顺序存储方式是较为适宜的。
(1)行主次序存取,即把二维数组看成行向量组成的一维结构。
此方式下的存储映象为:行主次序
(2)列主次序存取,即把二维数组看成列向量 组成的一维结构。
此方式下的存储映象为:列主次序

假设有一个3×4×2的三维数组A ,共有24个元素,其逻辑结构如图所示。
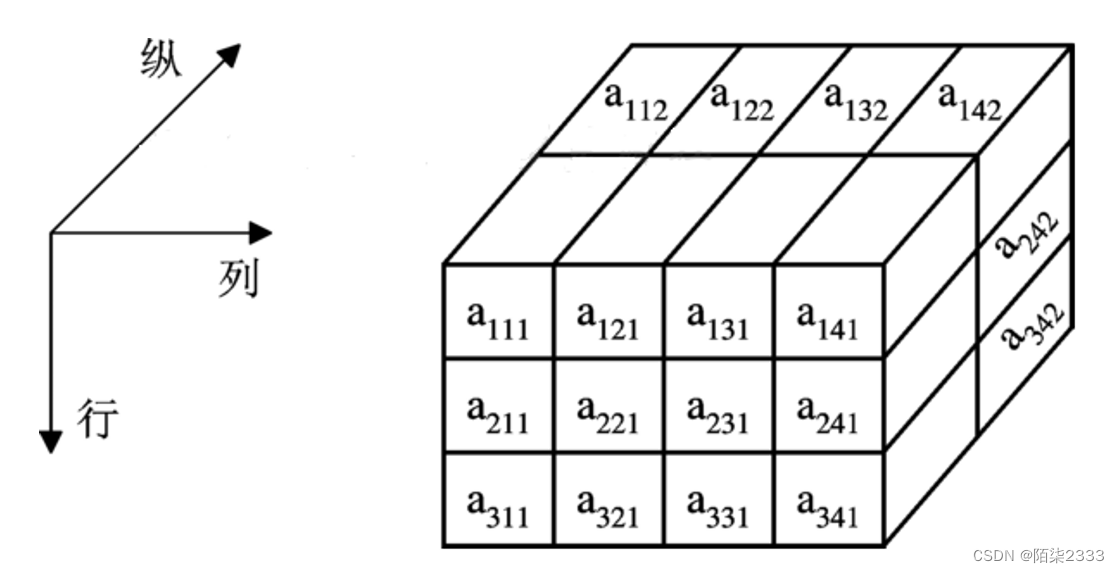
三维数组元素的标号由三个数字表示,即行、列、纵三个方向。
a142表示第1行,第4列,第2纵的元素。
如果对A3×4×2(下标从1开始)采用以行为主序的方法存放,即行下标变化最慢,纵下标变化最快,则顺序为:
a111,a112,a121,a122, …,a331,a332,a341,a342
采用以纵为主序的方法存放, 即纵下标变化最慢, 行下标变化最快, 则顺序为:
a111,a211,a311,a121,a221,a321,…,a132,a232,a332,a142,a242,a342
按上述两种方式顺序存储的数组,只要知道整个数组的起始地址、维数和每维的上下界,以及每个数组元素所占用的单元数,就可以将数组元素的存储地址表示为其下标的线性函数。
因此,顺序存储的数组是一种随机存取的结构。
3.二维数组的顺序存储
以二维数组Am×n为例,假设每个元素只占一个存储单元,“以行为主”存放数组,下标从1开始,首元素a11的地址为Loc[1, 1],求任意元素aij的地址。aij是排在第i行,第j列,并且前面的第i-1行有n×(i-1)个元素,第i行第j个元素前面还有j-1个元素。
由此得到如下地址计算公式: Loc[i, j]=Loc[1, 1]+n×(i-1)+(j-1)
根据计算公式,可以方便地求得aij的地址是Loc[i, j]。如果每个元素占size个存储单元,
则任意元素aij的地址计算公式为: Loc[i, j]=Loc[1, 1] + (n×(i-1)+j-1)×size
4.三维数组的顺序存储
三维数组A(1..r , 1..m , 1..n)可以看成是r个m×n的二维数组。

假定每个元素占一个存储单元,采用以行为主序的方法存放,即行下标r变化最慢, 纵下标n变化最快。 首元素a111的地址为Loc[1, 1, 1],求任意元素aijk的地址。
显然,ai11的地址为Loc[i, 1, 1]=Loc[1, 1, 1]+(i-1)×m×n, 因为在该元素之前, 有i-1个m×n的二维数组。由ai11的地址和二维数组的地址计算公式,不难得到三维数组任意元素aijk的地址:
Loc[i, j, k]=Loc[1, 1, 1]+(i-1)×m×n+(j-1)×n+(k-1) 其中1≤i≤r,1≤j≤m, 1≤k≤n。、
如果将三维数组推广到一般情况,即:用j1、j2、j3代替数组下标i、j、k, 并且j1、j2、j3的下限为c1、c2、c3,上限分别为d1、 d2、d3,每个元素占一个存储单元,则三维数组中任意元素a(j1, j2,j3)的地址为:
Loc[j1, j2, j3]=Loc[c1, c2, c3]+l×(d2-c2+1)×(d3-c3+1)×(j1-c1) +l×(d3-c3+1)×(j2-c2)+l×(j3-c3)
其中l为每个元素所占存储单元数。
令α1=l×(d2-c2+1)×(d3-c3+1), α2=l×(d3-c3+1), α3=1
则: Loc[j1, j2, j3]=Loc[c1, c2, c3]+α1×(j1-c1)+α2×(j2-c2)+α3(j3-c3)=Loc[c1, c2, c3]+∑αi×(ji-ci) (1≤i≤3)
由公式可知Loc[j1, j2, j3]与j1, j2, j3呈线性关系。
对于n维数组A(c1∶d1, c2∶d2,…, cn∶dn),我们只要把上式推广,就可以容易地得到n维数组中任意元素aj1j2…jn的存储地址的计算公式:
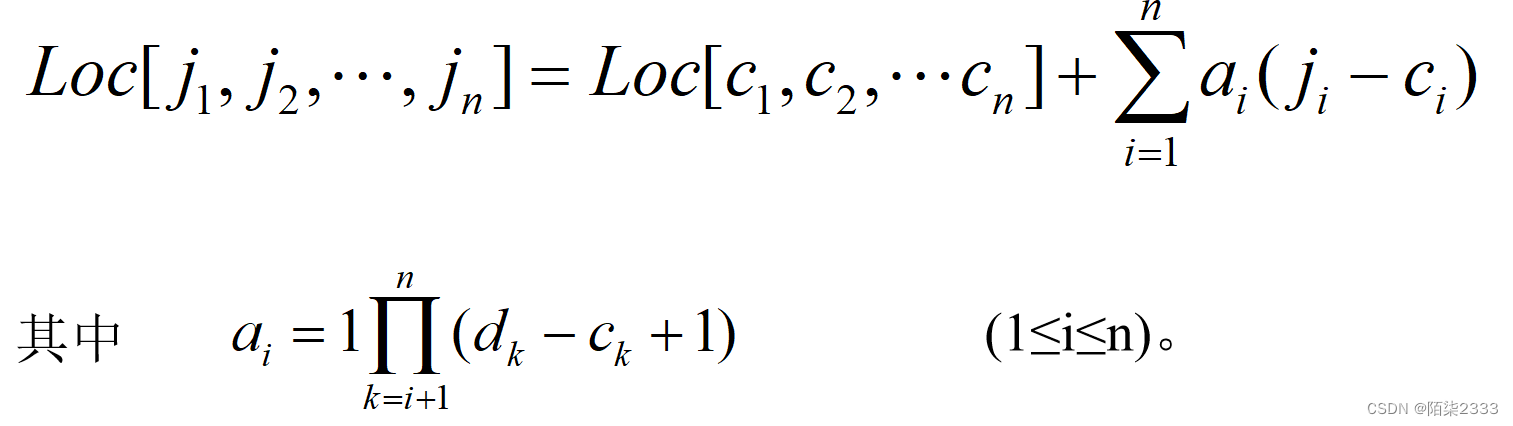
相关文章:
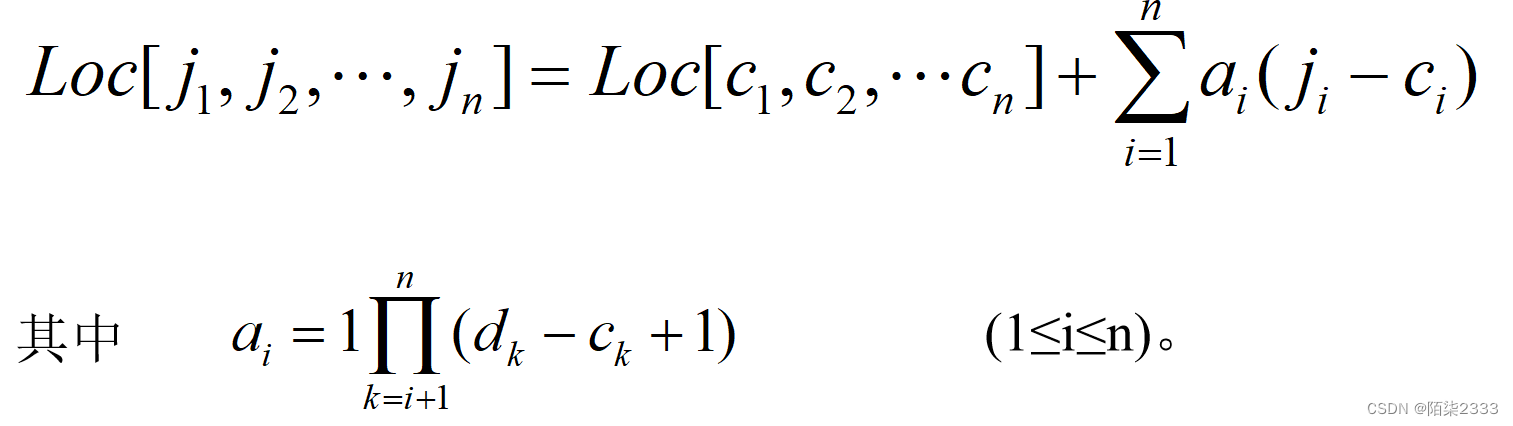
数据结构(超详细讲解!!)第二十节 数组
1.定义 1.概念 相同类型的数据元素的集合。 记作:A(A0,A1,…,Am-1) 二维数组可看作是每个数据元素都是相同类型的一维数组的一维数组。多维数组依此类推。 二维数组是数据元素为线性表的线性表。 A(A0,A1,……,An-1) 其中…...

【Android】Android Framework系列---CarPower深度睡眠STR
Android Framework系列—CarPower深度睡眠 之前博客说了CarPower的开机启动流程 这里分析一下,Android CarPower实现深度睡眠的流程。 首先,什么是深度睡眠(Deep Sleep)? Android进入Deep Sleep后,关闭屏幕、关闭CPU的电源,保持…...
【漏洞复现】Fastjson_1.2.47_rce
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现1、基础环境2、漏洞检测3、漏洞验证 1.5、深度利用1、反弹Shell 说明内容漏洞编号漏洞名称Fastjson_1.2.47_远程执行漏…...

玩转AIGC:如何选择最佳的Prompt提示词?
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

ELK搭建以及使用教程(多pipiline)
1、环境准备 服务器:Centos7 Jdk版本:1.8 Es版本:7.12.1 kibana版本:7.12.1 logstash版本:7.12.1 IP地址安装软件192.168.50.211Es,Kibana,logstash 2、安装docker 安装步骤参考:https:…...

小程序如何设置用户同意服务协议并上传头像和昵称
为了保护用户权益和提供更好的用户体验,设置一些必填项和必读协议是非常必要的。首先,用户必须阅读服务协议。服务协议是明确规定用户和商家之间权益和义务的文件。通过要求用户在下单前必须同意协议,可以确保用户在使用服务之前了解并同意相…...

6.4 例程:使用互斥量
这个例程为使用多线程配合互斥量进行点乘计算,相关的数据通过全局变量的形式存在,因此可以被各个线程访问;每个线程会在相关数据的不同区域上进行处理,主线程等待子线程完成操作后,将最后的结果打印出来。 代码如下 #…...
)
[算法日志]图论: 深度优先搜索(DFS)
[算法日志]图论: 深度优先搜索(DFS) 深度优先概论 深度优先搜索算法是一种遍历图这种数据结构的算法策略,其中心思想是朝图节点的一个方向不断跳转,当该节点无下一个节点或所有方向都遍历完时,便回溯朝上一个节点的另一个方向…...

这道经典SQL面试问题你会吗?
大家经常自嘲后端开发就是crud boy嘛,今天给大家看一道SQL题,我相信很多人写不出来。我们来看一下这个题目。 create table course (id int primary key,name varchar(32) not null ); create table student (id int primary key,name varchar(32) not …...

网络服务退出一个问题的解析
一、问题 在实际开发中遇到一个问题,解决的过程虽然不长,但确实是想得比较多,总结一下,以供参考。这是一个网络通信的服务端而且使用的是别人封装好的库,通信等都没有问题,但在退出时会报一个错误…...

第四次pta认证P测试
第一题 试题编号: 试题名称:整数排序 时间限制: 1.0s 内存限制: 128.0MB 【问题描述】 老师给定 10 个整数的序列,要求对其重新排序。排序要求: 1.奇数在前,偶数在后; 2.奇数按从大到小排序&am…...

mysql:B+树/事务
B树 : 为了数据库量身定做的数据结构 我们当前这里的讨论都是围绕 mysql 的 innodb 这个存储引擎来讨论的 其他存储引擎可能会用到hash 作为索引,此时就只能应对这种精准匹配的情况了 要了解 B树 我们先了解 B树, B树 是 B树 的改进 B树 有时候会写作 B-树 (这里的" -…...
python-在系统托盘显示CPU使用率和内存使用率
一、添加轮子 1.添加托盘区图标库 infi.systray from infi.systray import SysTrayIcon 2.添加图像处理库 Pillow from PIL import Image, ImageDraw, ImageFont 3.添加 psutil 来获取CPU、内存信息 import psutil 二、完整代码 from infi.systray import SysTrayIcon …...
构建mono-repo风格的脚手架库
前段时间阅读了 https://juejin.cn/post/7260144602471776311#heading-25 这篇文章;本文做一个梳理和笔记; 主要聚焦的知识点如下: 如何搭建脚手架工程如何开发调试如何处理命令行参数如何实现用户交互如何拷贝文件夹或文件如何动态生成文件…...
云安全—etcd攻击面
0x00 前言 本篇还是一样,先来说一说etcd是什么,干啥的,然后再来看看etcd的攻击面到底有哪些,做一个抛砖引玉的作用,如有不妥之处还请斧正 0x01 etcd 依旧还是按照问问题的方式来进行阐述,因为学到的东西…...
类锁和实例对象锁你分清了吗?
系列文章目录 文章目录 系列文章目录前言一、什么是锁竞争?二、什么是类锁?什么是实例对象锁?三、给类对象加锁不是锁住了整个类四、总结 前言 java选手们应该都对锁不陌生,加锁了就是为保证操作语句的原子性,如果你是…...
如何在麒麟上安装 ONLYOFFICE 桌面编辑器
我们很高兴地告诉大家,ONLYOFFICE 桌面编辑器现已上架麒麟软件商店。请阅读下文了解详情。 关于麒麟 麒麟是一款国产操作系统,主要是为了满足中国市场的需求和偏好而设计的。 它能够与各种硬件平台和软件应用程序的广泛兼容,因而受到认可。…...

记录:如何编写linux驱动,用module的方式
记录:如何编写Linux驱动,用module的方式 记录:如何编写Linux驱动,用module的方式参考记录:如何编写Linux驱动,用module的方式 编写一个 Linux 的驱动,用 module 方式开发,一般来说,编写一个 Linux 的驱动,需要遵循以下步骤: 确定设备的类型和功能,以及它在系统中的…...
3款免费又好用的 Docker 可视化管理工具
前言 Docker提供了命令行工具(Docker CLI)来管理Docker容器、镜像、网络和数据卷等Docker组件。我们也可以使用可视化管理工具来更方便地查看和管理Docker容器、镜像、网络和数据卷等Docker组件。今天我们来介绍3款免费且好用的 Docker 可视化管理工具。…...
C语言--判断一个年份是否是闰年(详解)
一.闰年的定义 闰年是指在公历(格里高利历)中,年份可以被4整除但不能被100整除的年份,或者可以被400整除的年份。简单来说,闰年是一个比平年多出一天的年份,即2月有29天。闰年的目的是校准公历与地球公转周…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
