编码格式科普ASCII unicode utf-8 usc-2 GB2312
1.ASCII（标准版） 可以表示所有英文字符（包括大写和小写）和数字，长度为7bit，最多可以表示0-127 个值，2的7次方个数字。比如比如“a” 对照ASCII码的值为97（十进制）或1100001 （七位二进制）
2.ASCII（拓展版）长度为8bit ，最多可表示0-256个值，在ASCII标准版的基础上，增加了欧洲文字和特殊字符
3.unicode （以及升级版的usc-2和utf-8）一种全球化的标准字符码，包含了全世界所有的语言、文字、符号，usc-2和utf-8为unicode的升级版。usc-2用16位（16比特）（16bit）（2b）(2byte)（2字节）表示一个字符，最多可以表示2的16次方个字符，即65535个字符。utf-8是usc-2的升级版（包含usc-2的所有字符，向下兼容），用1-4个字节表示一个字符，即最多表示4个byte即2的32次方=4294967296（十进制）个数字。“中”用utf-8表示为“%u4E2D” ，而用unicode表示为“\u4e2d”
4.GB2312 ，国产的中文字符集，只能表示简体，无法表示繁体，时代的产物，已被淘汰
5.GBK，国产的中文字符集，GB2312的升级版，兼容GB2312
相关文章：
编码格式科普ASCII unicode utf-8 usc-2 GB2312
1.ASCII（标准版） 可以表示所有英文字符（包括大写和小写）和数字，长度为7bit，最多可以表示0-127 个值，2的7次方个数字。比如比如“a” 对照ASCII码的值为97（十进制）或11000…...
Pycharm中新建一个文件夹下__init__.py文件有什么用
在PyCharm中新建一个文件夹下的__init__.py文件有以下几个作用： 声明文件夹为一个Python包：__init__.py文件的存在告诉Python解释器该文件夹是一个Python包。当你导入该文件夹下的模块时，Python会将其视为一个包而不是普通的文件夹。这允许你…...
OracleBulkCopy c#批量插入oracle数据库的方法
datatable中的数据 存入oracle表中，要求 二者字段名一致，如果不一致，通过这个实现对应： bulkCopy.ColumnMappings.Add("SERVNUMBER", "SN"); 首先要引入Oracle.DataAccess.dll文件（在oracle客户端…...
046_第三代软件开发-虚拟屏幕键盘
第三代软件开发-虚拟屏幕键盘 文章目录 第三代软件开发-虚拟屏幕键盘项目介绍虚拟屏幕键盘 关键字： Qt、 Qml、 虚拟键盘、 qtvirtualkeyboard、 自定义 项目介绍 欢迎来到我们的 QML & C 项目！这个项目结合了 QML（Qt Meta-Object L…...
MySQL主从搭建，实现读写分离（基于docker)
一 主从配置原理 mysql主从配置的流程大体如图： 1）master会将变动记录到二进制日志里面； 2）master有一个I/O线程将二进制日志发送到slave; 3) slave有一个I/O线程把master发送的二进制写入到relay日志里面； 4…...
uni-app android picker选择默认月份
微信小程序选中月份后下次再点开是上次的选中的月份，而编译的android应用只默认当前月份 <picker mode"date" ref"picker" :disabled"disabled" :value"date" fields"month" change"bindDateChange&quo…...
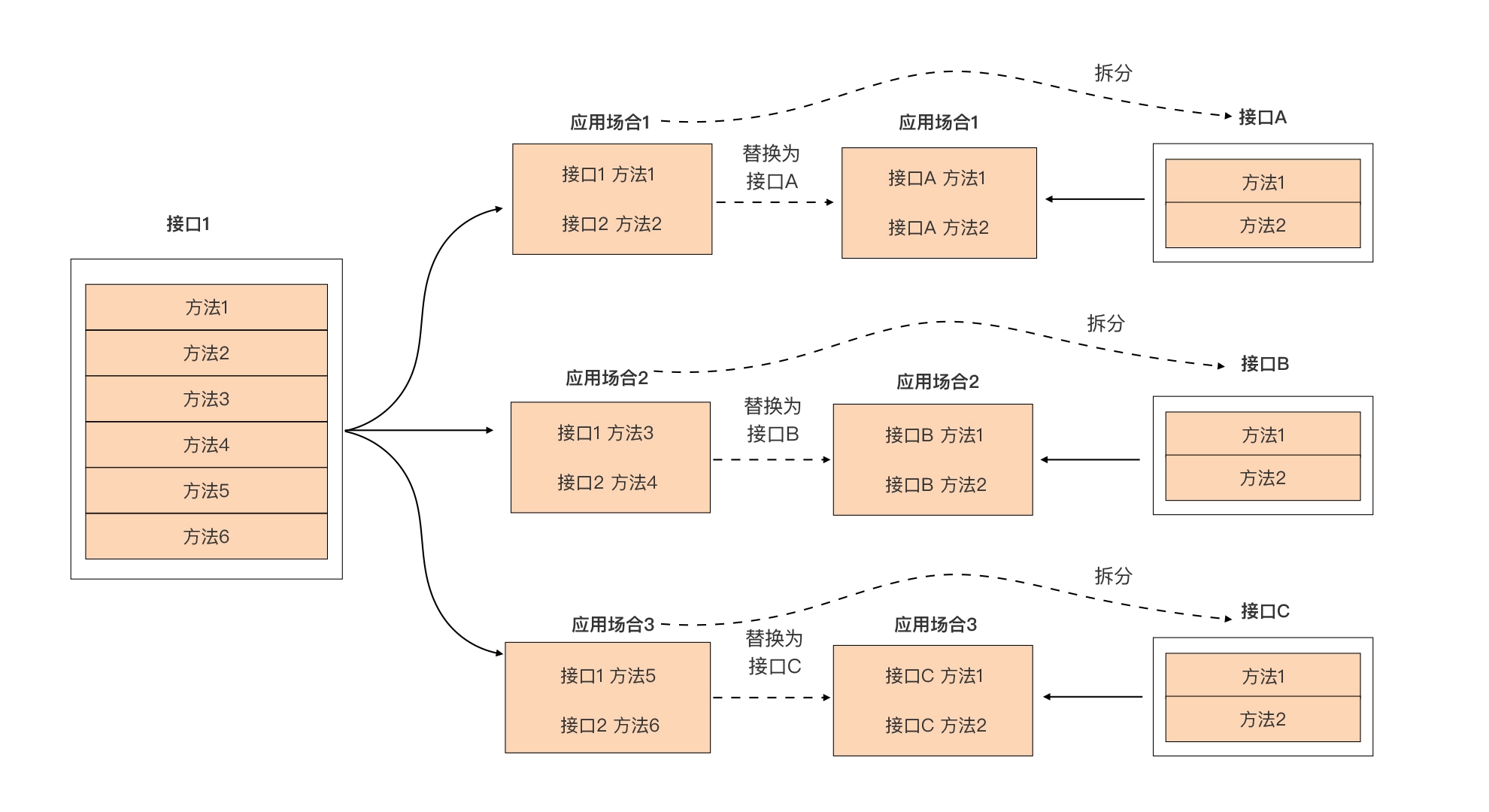
Go 接口-契约介绍
Go 接口-契约介绍 文章目录 Go 接口-契约介绍一、接口基本介绍1.1 接口类型介绍1.2 为什么要使用接口1.3 面向接口编程1.4 接口的定义 二、空接口2.1 空接口的定义2.2 空接口的应用2.2.1 空接口作为函数的参数2.2.2 空接口作为map的值 2.3 接口类型变量2.4 类型断言 三、尽量定…...
变压器试验VR虚拟仿真操作培训提升受训者技能水平
VR电气设备安装模拟仿真实训系统是一种利用虚拟现实技术来模拟电气设备安装过程的培训系统。它能够为学员提供一个真实、安全、高效的学习环境，帮助他们更好地掌握电气设备的安装技能。 华锐视点采用VR虚拟现实技术、MR混合现实技术、虚拟仿真技术、三维建模技术、人…...
Mastering Makefile：模块化编程技巧与经验分享
在Linux项目管理中，Makefile是一个强大的工具，它可以帮助我们自动化编译和测试过程。然而，随着项目的增长，Makefile可能会变得越来越复杂，难以管理。在这篇文章中，我将分享一些模块化编程的技巧和经验&…...
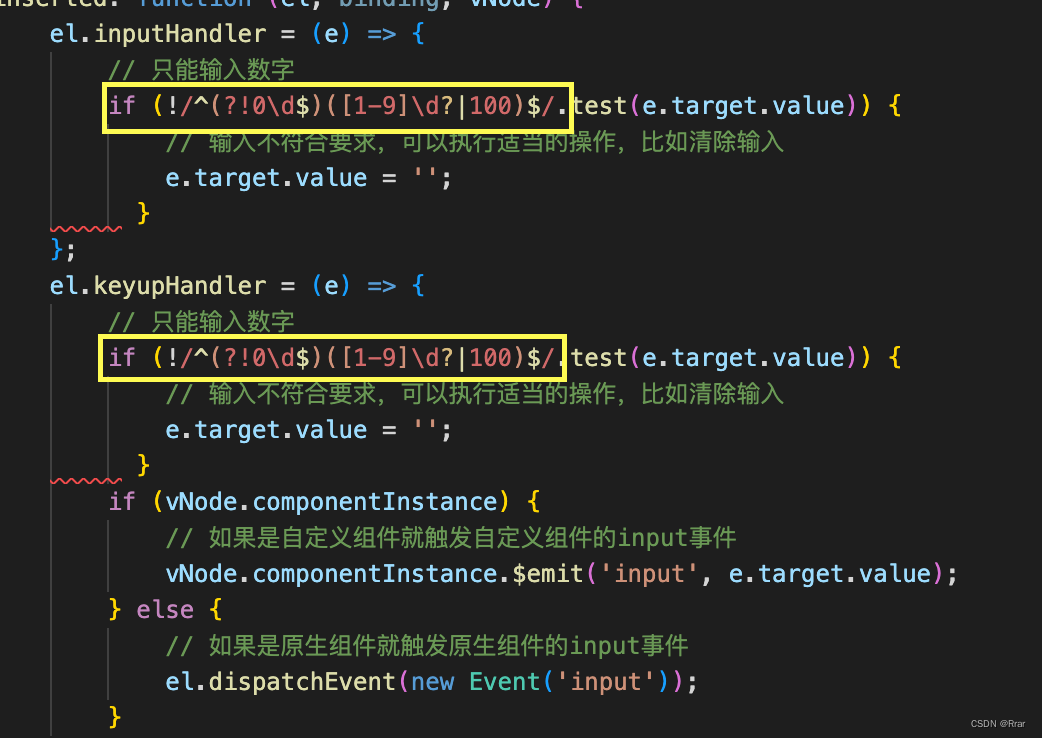
el-input输入校验插件（正则表达式）
使用方法：在main.js文件中注册插件然后直接在<el-input>加入‘v-插件名’ (1)在main.js文件： // 只能输入数字指令 import onlyNumber from /directive/only-number; Vue.use(onlyNumber); （2）在src/directive文件夹中 &a…...
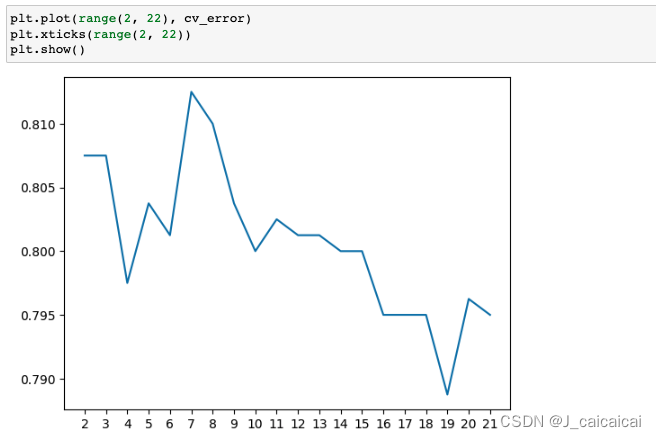
【Matplotlib】plt.plot() X轴横坐标展示完整整数坐标
比如说，我的数据应该是 x轴从2到21的20个整数 y轴对应值 但是直接plot的话x轴显示居然有小数点什么鬼 可以这样改...
左手 Jira，右手 Polarion，驶入互联网和制造业十字路口的新能源汽车
笔者之前一直在互联网公司从事软件研发，创立 Bytebase 之后，才开始接触到各行各业的用户。最近来自汽车行业的客户不少，所以就翻翻相关资料。周末微信收到了一条推送，提到汽车行业的软件研发管理，也由此了解到了 Polar…...
网络安全（黑客）-0基础小白自学
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类，我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术，而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高； 二、则是发展相对成熟…...
ActiveMQ、RabbitMQ、RocketMQ、Kafka介绍
一、消息中间件的使用场景 消息中间件的使用场景总结就是六个字：解耦、异步、削峰 1.解耦 如果我方系统A要与三方B系统进行数据对接，推送系统人员信息，通常我们会使用接口开发来进行。但是如果运维期间B系统进行了调整，或者推送过…...
unity打AB包，AssetBundle预制体与图集（二）
第二步：加载AB包的资源，用于显示 using System.Collections; using System.Collections.Generic; using System.IO; using UnityEngine; using UnityEngine.Networking; using UnityEngine.U2D; using UnityEngine.UI;public class GameLaunch : MonoBe…...
【网络安全 --- web服务器解析漏洞】IIS，Apache，Nginx中间件常见解析漏洞
一，工具及环境准备 以下都是超详细保姆级安装教程，缺什么安装什么即可（提供镜像工具资源） 1-1 VMware 16.0 安装 【网络安全 --- 工具安装】VMware 16.0 详细安装过程（提供资源）-CSDN博客文章浏览阅读20…...
Python基础——注释、缩进、语法、标识符、关键字
注释 Python中单行注释用#表示，多行注释由3对双引号或单引号包裹：可以使用快捷键CTRLR进行注释 # 我是单行注释"""我是多行注释 """缩进 python使用“缩进”即一行代码前的空白区域确定代码之间的逻辑关系和层次关系。…...
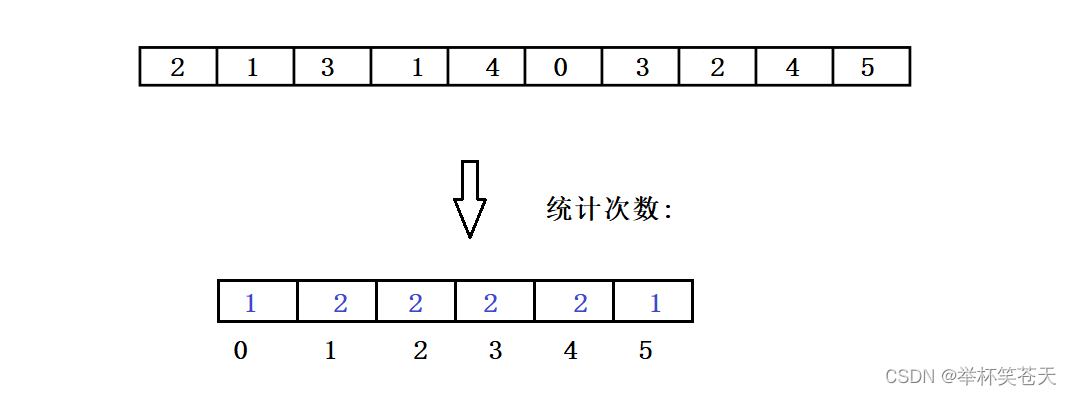
排序算法的分析及实现
目录 1. 排序 1.1. 排序的概念 1.2. 排序的稳定性 1.3. 内部排序和外部排序 2. 直接插入排序 2.1. 直接插入排序 2.2. 直接插入排序的两种情况 1. 情况一 2. 情况二 2.3. 直接插入排序的单趟排序 2.4. 直接插入排序的完整实现 2.5. 直接插入排序的时…...
rancher或者其他容器平台使用非root用户启动jar
场景： java程序打成镜像，在rancher上运行，默认是root账户，发现hdfs或者hive不允许root账户操作；所以打算用费root账户启动jar，使其具有hive和hdfs的操作权限。 Dockerfile entrypoint.sh 思路就是上面这样…...
Scrapy使用和学习笔记
前言 Scrapy是非常优秀的一个爬虫框架，基于twisted异步编程框架。yield的使用如此美妙。基于调度器，下载器可以对scrapy扩展编程。插件也是非常丰富，和Selenium，PlayWright集成也比较轻松。 当然，对网页中的ajax请求…...
web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段： 构建阶段（Build Stage）：…...
[2025CVPR]DeepVideo-R1：基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈，在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度，导致： 梯度抑制：当新旧策略差异过大时梯度消失收敛困难：策略无法充分优化# 传统GRPO的梯…...
Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
《用户共鸣指数（E）驱动品牌大模型种草：如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代，情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现，消费者对内容的“有感”程度，正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡（如 HAProxy、AWS NLB、阿里 SLB）发起上游连接时，将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后，ngx_stream_realip_module 从中提取原始信息…...
HarmonyOS运动开发：如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit（传感器服务）# 前言 在运动类应用中，运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据，如配速、距离、卡路里消耗等，用户可以更清晰…...
08. C#入门系列【类的基本概念】：开启编程世界的奇妙冒险
C#入门系列【类的基本概念】：开启编程世界的奇妙冒险 嘿，各位编程小白探险家！欢迎来到 C# 的奇幻大陆！今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类！别害怕，跟着我，保准让你轻松搞…...
宇树科技，改名了！
提到国内具身智能和机器人领域的代表企业，那宇树科技（Unitree）必须名列其榜。 最近，宇树科技的一项新变动消息在业界引发了不少关注和讨论，即： 宇树向其合作伙伴发布了一封公司名称变更函称，因…...
省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
CVPR2025重磅突破：AnomalyAny框架实现单样本生成逼真异常数据，破解视觉检测瓶颈！
本文介绍了一种名为AnomalyAny的创新框架，该方法利用Stable Diffusion的强大生成能力，仅需单个正常样本和文本描述，即可生成逼真且多样化的异常样本，有效解决了视觉异常检测中异常样本稀缺的难题，为工业质检、医疗影像…...