扫地机器人(蓝桥杯C/C++)
题目描述
小明公司的办公区有一条长长的走廊,由 NN 个方格区域组成,如下图所示。

走廊内部署了 KK 台扫地机器人,其中第 ii 台在第 A_iAi 个方格区域中。已知扫地机器人每分钟可以移动到左右相邻的方格中,并将该区域清扫干净。
请你编写一个程序,计算每台机器人的清扫路线,使得
-
它们最终都返回出发方格,
-
每个方格区域都至少被清扫一遍,
-
从机器人开始行动到最后一台机器人归位花费的时间最少。
注意多台机器人可以同时清扫同一方块区域,它们不会互相影响。
输出最少花费的时间。 在上图所示的例子中,最少花费时间是 6。第一台路线:2-1-2-3-4-3-2,清 扫了 1、2、3、4 号区域。第二台路线 5-6-7-6-5,清扫了 5、6、7。第三台路线 10-9-8-9-10,清扫了 8、9 和 10。
输入描述
第一行包含两个整数 N,K。
接下来 K 行,每行一个整数 Ai。
![]()
输出描述
输出一个整数表示答案。

我们不妨按照这样的思路解题:
我们引入这样的例子:
比如给一根绳,围成一个矩形,求在长和宽为多少时矩形面积最大
那么,可求得当长和宽相等时矩形面积最大,长和宽之间的差距为0
那么用同样的思路,有n个格需要清扫,有k个机器人,我们希望每个机器人能够平分任务而且尽量不重复清扫,这样消耗时间是最短的,消耗时间设为x
所以,这里用二分查找计算出最小值
剩下的思路不好表达,不妨结合代码来说
total代表前(n-1)个机器人已经清扫到的格数,这里我们把机器人的任务设定为需要清扫完右边的并且在下一个机器人左边的方格
首先,目前这个机器人根据目前的x值能够到达total位置(这个机器人能够弥补上一个机器人没有清扫的格数),这个是必须要满足的条件,如果下一个机器人不能够填补上一个机器人留下的漏洞,那么漏洞会越积越大,这肯定是不行的
然后,满足了这个条件后,就需要优中选优,这里我们分为两种情况讨论:
1.如果前一个机器人能够完成自己的任务,即目前这个机器人不用往左边清扫了,total直接加上目前的x值再减一就是已经清扫的范围
2.如果前一个机器人不能完成自己的任务,那么需要先完成前一个机器人剩下的任务,然后再开始自己的工作
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+7;
int n,m;
int robot_list[maxn];bool check(int x)
{int total=0;for(int i=0;i<m;i++){if(robot_list[i]-x<=total)//能够到达total位置,弥补前面一个机器人留的未清扫区域 {if(robot_list[i]<=total) total=robot_list[i]+x-1;else total+=x;//左边没扫完 }else return false; //不能够到达total位置,不能弥补前面一个机器人留的未清扫区域,直接失败 }return total>=n;//这种情况下才成立,返回true
}
int main()
{cin>>n>>m;for(int i=0;i<m;i++){cin>>robot_list[i];}sort(robot_list,robot_list+m);//排序int left=1,right=n,middle=0,ans=0;while(left<=right){middle=(right+left)/2;if(check(middle)){right=middle-1;ans=middle;}else{ left=middle+1; } } cout<<(ans-1)*2<<endl;return 0;
}相关文章:

扫地机器人(蓝桥杯C/C++)
题目描述 小明公司的办公区有一条长长的走廊,由 NN 个方格区域组成,如下图所示。 走廊内部署了 KK 台扫地机器人,其中第 ii 台在第 A_iAi 个方格区域中。已知扫地机器人每分钟可以移动到左右相邻的方格中,并将该区域清扫干净。…...
如何理解API?API 是如何工作的?(5分钟诠释)
大家可能最近经常听到 API 这个概念,那什么是API,它又有什么特点和好处呢? wiki 百科镇楼 …[APIs are] a set of subroutine definitions, protocols, and tools for building application software. In general terms, it’s a set of cle…...

PAT--1111 对称日
央视新闻发了一条微博,指出 2020 年有个罕见的“对称日”,即 2020 年 2 月 2 日,按照 年年年年月月日日 格式组成的字符串 20200202 是完全对称的。 给定任意一个日期,本题就请你写程序判断一下,这是不是一个对称日&a…...

前端纯函数和副作用概念,且在react上的体现详解
什么是纯函数 纯函数是这样一种函数,即相同的输入,永远会得到相同的输出的函数,而且没有任何可观察的副作用。 什么是副作用 副作用是在计算结果的过程中,系统状态的一种变化,或者与外部世界进行的可观察的交互。 个…...

转行软件测试3年了,听前辈说测试前途是IT里最low的,我慌了......
互联网行业的技术岗位一般分为研发、测试和运维,虽然前些年测试一直都不如研发岗位那么吃香。但现在随着国内对软件测试的重视,我国互联网企业对软件测试的需求在未来还将继续增大。听起来软件测试的就业形势一片大好,那么到底软件测试的发展…...
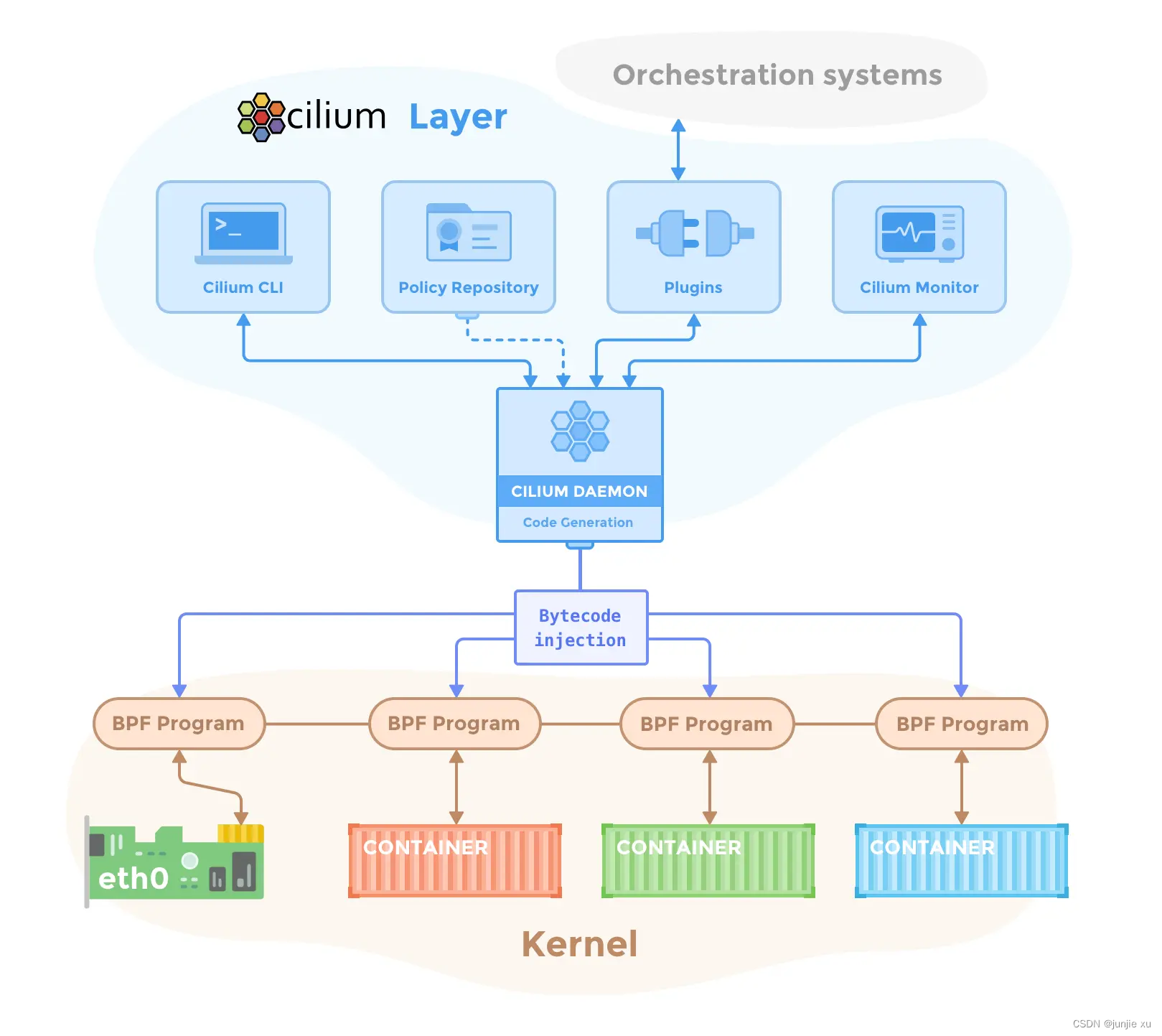
CNI 网络流量 5.1 Cilium 介绍和原理
文章目录简介安装组件和原理Cilium-agent初始化IPAMCNICilium cli 的使用bpfMap 的操作Cilium-agentEbpf简介 Cilium 是一个用于容器网络领域的开源项目,主要是面向容器而使用,用于提供并透明地保护应用程序工作负载(如应用程序容器或进程&a…...
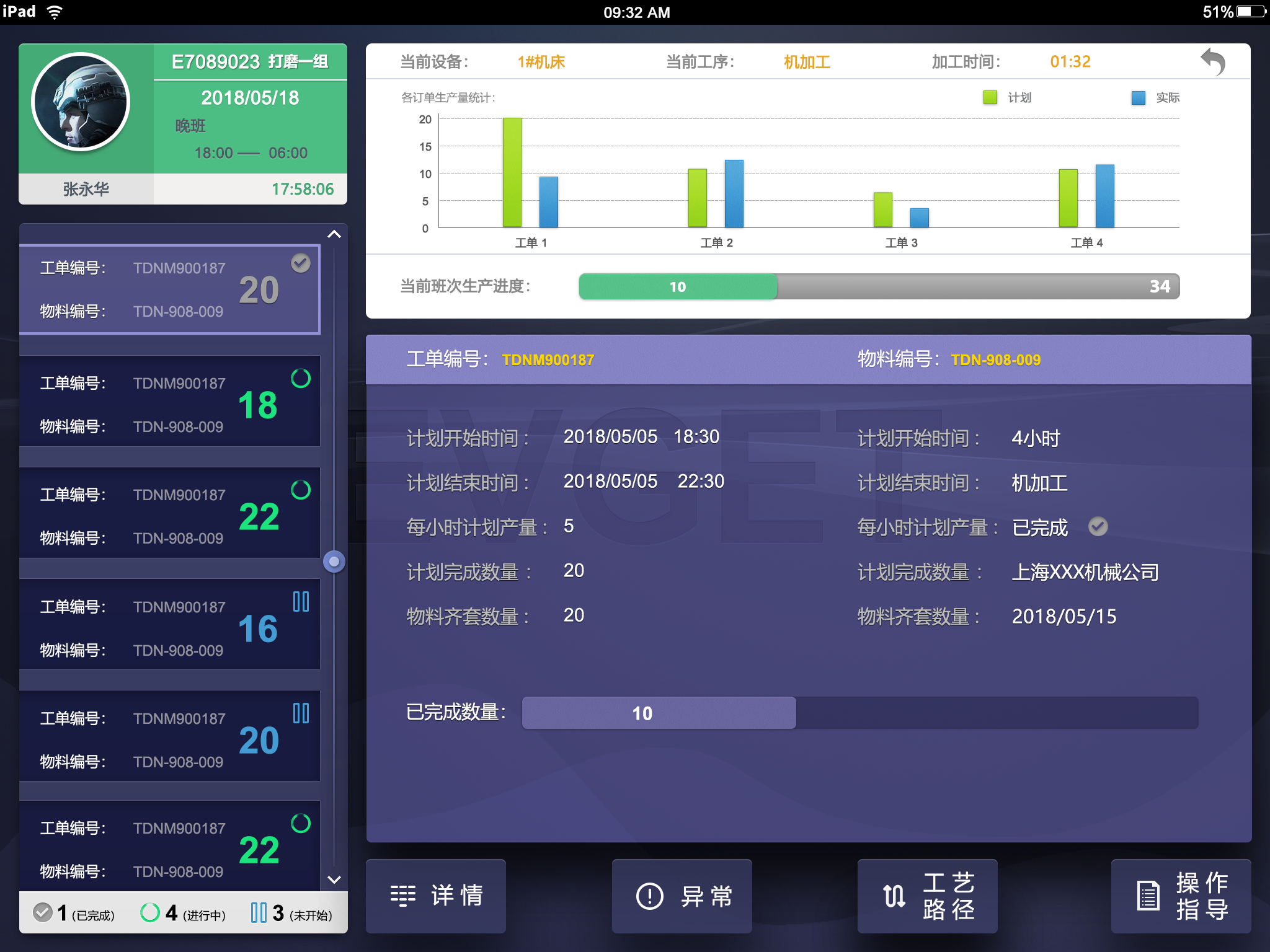
机加行业MES解决方案,助力企业打造数字化透明车间
机械加工行业的主要原材料占整个生产物料成本的95%~99%,以挖掘机为例,原材料有各种规格的钢板、焊丝、焊条、油漆以及各种气体等,其中主要原材料是钢板,占原材料比率的98%以上。 因此机械加工mes的原材料管理是机械加工行业信息化…...
C/C++每日一练(20230227)
目录 1. 按要求排序数组 ★ 2. Z 字形变换 ★★ 3. 下一个排列 ★★ 1. 按要求排序数组 给你一个整数数组 arr 。请你将数组中的元素按照其二进制表示中,数字 1 的数目升序排序。 如果存在多个数字二进制中 1 的数目相同,则必须将它们按照数值大小…...

总结SpringBoot1.x迁移到2.x需要注意的问题
SpringBoot1.x和SpringBoot2.x版本差异化还是比较大的,有些三方依赖组件有些是基于2.0版本为标准升级的,当我们将项目由1.0升级到2.0时会出现依赖的方法不存在或方法错误,需要逐个去调整,下面总结了我们升级实践过程中遇到的一些问…...

Api接口小知识
应用程序接口API(Application Programming Interface),是提供特定业务输出能力、连接不同系统的一种约定。这里包括外部系统与提供服务的系统(中控系统)或者后台不同的系统之间的交互点。包括外部接口、内部接口、内部接口有包括&…...

「JVM 高效并发」Java 协程
Java 语言抽象和隐藏了各种操作系统线程差异性的接口,这曾经是它区别于其他编程语言的一大优势,但在某些场景下,却已经出现了疲态; 文章目录1. 内核线程的局限2. 协程的复苏3. Java 的解决方案1. 内核线程的局限 在微服务架构中&…...

Web Spider案例 网洛者 第一题 JS混淆加密 - 反hook操作 练习(五)
文章目录一、资源推荐二、第一题 JS混淆加密 - 反hook操作2.1 过控制台反调试(debugger)2.2 开始逆向分析三、python具体实现代码四、记录一下,execjs调用混淆JS报错的问题总结提示:以下是本篇文章正文内容,下面案例可供参考 一、资源推荐 …...
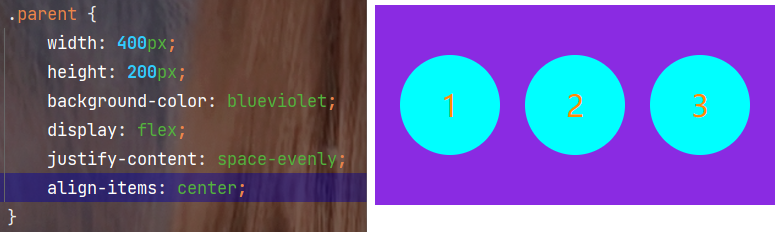
前端基础之CSS扫盲
文章目录一. CSS基本规范1. 基本语法格式2. 在HTML引入CSS3. 选择器分类二. CSS常用属性1. 文本属性2. 文本格式3. 背景属性4. 圆角矩形和圆5. 元素的显示模式6. CSS盒子模型7. 弹性布局光使用HTML来写一个前端页面的话其实只是写了一个大体的框架, 整体的页面并不工整美观, 而…...

mysql组复制、mysql路由器、mysql的MHA高可用
文章目录前言一、mysql组复制1.实验机配置2.测试二、mysql路由器三、mysql之MHA高可用1.MHA概念1.创建一主两从集群2.MHA部署3.故障切换前言 一、mysql组复制 1.实验机配置 server1配置 首先停止数据库 [rootserver1 mysql]# /etc/init.d/mysqld stop Shutting down MySQL..…...

一篇搞懂springboot多数据源
好文推荐 https://zhuanlan.zhihu.com/p/563949762 mybatis 配置多数据源 参考文章 https://blog.csdn.net/qq_38353700/article/details/118583828 使用mybatis配置多数据源我接触过的有两种方式,一种是通过java config的方式手动配置两个数据源,…...
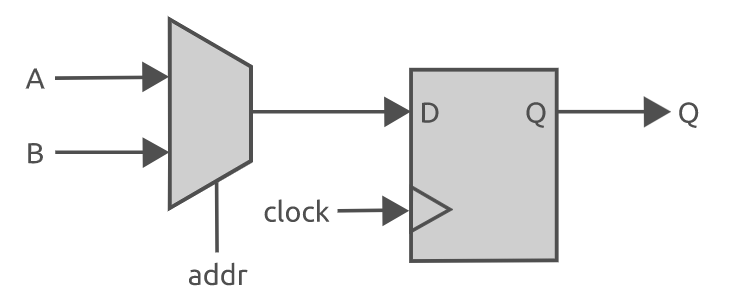
Verilog 数据类型和数组简介
在这篇文章将讨论 verilog 中最常用的数据类型,包括对数据表示,线网类型、变量类型,向量类型和数组的讨论。尽管 verilog 被认为是一种弱类型语言(loosely typed),但设计者仍必须在 Verilog 设计中为每个端…...

【数据结构】时间复杂度和空间复杂度以及相关OJ题的详解分析
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录1.算法效率1.1 如何衡…...

31--Vue-前端开发-Vue语法
一、前端-Vue介绍 1.前端介绍 1、HTML(5)、CSS(3)、JavaScript(ES5、ES6):编写一个个的页面 ----> 给后端(PHP、Python、Go、Java) ----> 后端嵌入模板语法 ----> 后端渲染完数据 ----> 返回数据给前端 ----> 在浏览器中查看 2、Ajax的出现 -> 后台发送异…...

这份IC设计必读书单,值得所有IC设计工程师一看!
《综合与时序分析的设计约束》 作者:Sridhar Gangadharan 本书为集成电路时序约束设计的指南,指导读者通过指定的时序要求,充分发挥IC设计的性能。本书内容包括受时序约束的关键环节的设计流程、综合时序分析、静态时序分析和布局布线等。本书…...
Acwing 蓝桥杯 第一章 递归与递推
我上周在干什么,感觉我上周啥也没训,本来两天一次的vp也没v很寄啊,再这样下去真不行了先总结一下如何爆搜:先去确定好枚举的对象枚举的对象很重要!!这直接影响了复杂度然后就是去想递归树就好了一、确定状态…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
