【单目测距】单目相机测距(三)
文章目录
- 一、前言
- 二、测距代码
- 2.1、地面有坡度
- 2.2、python代码
- 2.2.1、旋转矩阵转角度
- 2.2.2、角度转旋转矩阵
- 2.2.3、三维旋转原理 (Rotation 原理)
- 2.2.4、完整代码
- 2.3、c++ 代码
一、前言
- 上篇博客【单目测距】单目相机测距(二) 有讲到当相机不是理想状态,实际情况如相机安装时候有角度偏差,需要对相机进行标定。同时也分析影响测距误差的多个因素以及各个因素影响权重。
- 上述都是基于地面与自身平行,当地面存在坡度尤其是上下坡度的时候。此时测距误差会非常之大。如果有 1° 坡度,那么目标在 10 m 处测距就有 20 cm 误差。
- 如果我们提前已知到地面的坡度 sigma ,我们就应该实时去修正相机外参,此片博客提供传入地面角度,实时修正相机外参的思路与代码。
二、测距代码
- 先回顾一下往期测距代码【单目测距】单目相机测距(二)
- 输入相机内参、外参、相机高度是提前标定完成
- 目标像素点由目标检测 bbox 求出。
import numpy as nph = 1.5 # 相机离地面1.5m高
pitch = -0.023797440420123328 # 弧度
pixe_x, pixe_y = 888, 700 # 图像像素点,接地点
CameraMat = np.array([[1008, 0, 945],[0, 1009, 537],[0, 0, 1]]) # 相机内参R = np.array([[-0.0330564609, 0.0238237337, 0.999169505],[0.999452124, -0.000862625046, 0.0330863791, ],[0.00165014972, 0.999715802, -0.0237821659]]) # 旋转矩阵
T = np.array([0, 0, -1.5])sigma = np.arctan((pixe_y - CameraMat[1][2]) / CameraMat[1][1])
z = h * np.cos(sigma) / np.sin(sigma + pitch) # 深度
x_pixe, y_pixe = 2 * CameraMat[0][2] - pixe_x, 2 * CameraMat[1][2] - pixe_y # 根据自定坐标系选择是否中心对称转换
camera_x = z * (x_pixe / CameraMat[0][0] - CameraMat[0][2] / CameraMat[0][0])
camera_y = z * (y_pixe / CameraMat[1][1] - CameraMat[1][2] / CameraMat[1][1])
camera_z = z
distance_machine_direction = R[0][0] * camera_x + R[0][1] * camera_y + R[0][2] * camera_z + T[0] # 纵向距离
distance_transverse_direction = R[1][0] * camera_x + R[1][1] * camera_y + R[1][2] * camera_z + T[1] # 横向距离
print(distance_machine_direction, distance_transverse_direction)
2.1、地面有坡度
- 根据前面分析,如果地面有坡度,我们应该实时去修正相机外参。具体怎么做,也很简单。就是实时去更新我们的 pitch 角与相机的外参。
- 我们前提是需要知道地面坡度是多少,关于如何获取地面坡度,以后有机会再谈。
2.2、python代码
python 从旋转矩阵转化到角度、从角度到转化矩阵,主要用到 scipy 库中的 Rotation。
2.2.1、旋转矩阵转角度
import numpy as np
from scipy.spatial.transform import Rotationr = np.array([-0.0517, -0.0611, 0.9968, 0.9987, 0.0011, 0.0519, -0.0042, 0.9981, 0.0609]).reshape(3, 3)
euler_r = Rotation.from_matrix(r).as_euler('zxy', degrees=False) # zxy 是 外旋顺序。degrees False 显示弧度,True 显示角度
print(euler_r)# [ 1.56967277 -0.0518037 1.50976086]
2.2.2、角度转旋转矩阵
from scipy.spatial.transform import Rotationeuler_r = [1.56967277, -0.0518037, 1.50976086]
new_r = Rotation.from_euler("zxy", [euler_r[0], euler_r[1], euler_r[2]], degrees=False).as_matrix()
2.2.3、三维旋转原理 (Rotation 原理)
import numpy as np
from scipy.spatial.transform import Rotationdef get_r_matrix(str, alpha):sin = -np.sin(alpha)cos = np.cos(alpha)res = np.eye(3)if str == "z":res = np.array([[cos, sin, 0],[-sin, cos, 0],[0, 0, 1]])elif str == "y":res = np.array([[cos, 0, -sin],[0, 1, 0],[sin, 0, cos]])elif str == "x":res = np.array([[1, 0, 0],[0, cos, sin],[0, -sin, cos]])return reseuler_r = [1.56967277, -0.0518037, 1.50976086]
a, b, c = euler_r[0], euler_r[1], euler_r[2]z = get_r_matrix("z", a)
x = get_r_matrix("x", b)
y = get_r_matrix("y", c)
mtx = y @ x @ z
mtx_1 = Rotation.from_euler("zxy", [a, b, c], degrees=False).as_matrix()
print(mtx, mtx_1) # 结果完全一致
2.2.4、完整代码
综上所述,可得
import numpy as np
from scipy.spatial.transform import Rotationdiff_pitch = -0.01 # 假设当前地面坡度为 -0.01 弧度
h = 1.5 # 相机离地面1.5m高
pitch = -0.023797440420123328 # 弧度
pitch = pitch + diff_pitch
pixe_x, pixe_y = 888, 700 # 图像像素点,接地点
CameraMat = np.array([[1008, 0, 945],[0, 1009, 537],[0, 0, 1]]) # 相机内参original_r = np.array([[-0.0330564609, 0.0238237337, 0.999169505],[0.999452124, -0.000862625046, 0.0330863791],[0.00165014972, 0.999715802, -0.0237821659]]) # 旋转矩阵
euler_r = Rotation.from_matrix(original_r).as_euler('zxy', degrees=False)
R = Rotation.from_euler("zxy", [euler_r[0], euler_r[1], euler_r[2] + diff_pitch], degrees=False).as_matrix()T = np.array([0, 0, -1.5]) # 平移矩阵sigma = np.arctan((pixe_y - CameraMat[1][2]) / CameraMat[1][1])
z = h * np.cos(sigma) / np.sin(sigma + pitch) # 深度
x_pixe, y_pixe = 2 * CameraMat[0][2] - pixe_x, 2 * CameraMat[1][2] - pixe_y # 根据自定坐标系选择是否中心对称转换
camera_x = z * (x_pixe / CameraMat[0][0] - CameraMat[0][2] / CameraMat[0][0])
camera_y = z * (y_pixe / CameraMat[1][1] - CameraMat[1][2] / CameraMat[1][1])
camera_z = z
distance_machine_direction = R[0][0] * camera_x + R[0][1] * camera_y + R[0][2] * camera_z + T[0] # 纵向距离
distance_transverse_direction = R[1][0] * camera_x + R[1][1] * camera_y + R[1][2] * camera_z + T[1] # 横向距离
print(distance_machine_direction, distance_transverse_direction)
2.3、c++ 代码
知道了 2.2.3 中的三维旋转原理,那我们利用矩阵乘法就可以轻松获得新外参啦
double pitchDiff = -0.01;cv::Mat initR = (cv::Mat_<double>(3,3) << -0.0330564609, 0.0238237337, 0.999169505,0.999452124, -0.000862625046, 0.0330863791, 0.00165014972, 0.999715802, -0.0237821659); // 相机初始外参cv::Mat pitchR = (cv::Mat_<double>(3, 3) << cos(pitchDiff), 0, sin(pitchDiff), 0, 1, 0, -sin(pitchDiff), 0, cos(pitchDiff));cv::Mat curR = pitchR * initR;
相关文章:

【单目测距】单目相机测距(三)
文章目录 一、前言二、测距代码2.1、地面有坡度2.2、python代码2.2.1、旋转矩阵转角度2.2.2、角度转旋转矩阵2.2.3、三维旋转原理 (Rotation 原理)2.2.4、完整代码 2.3、c 代码 一、前言 上篇博客【单目测距】单目相机测距(二) 有讲到当相机不是理想状态…...

Evaluating Large Language Models: A Comprehensive Survey
本文是LLM系列文章,针对《Evaluating Large Language Models: A Comprehensive Survey》的翻译。 评估大型语言模型:一项综合调查 摘要1 引言2 分类和路线图3 知识和能力评估4 对齐评估5 安全评估6 专业LLM评估7 评估组织8 未来方向9 结论 摘要 大型语…...

ElasticSearch 实现 全文检索 支持(PDF、TXT、Word、HTML等文件)通过 ingest-attachment 插件实现 文档的检索
一、Attachment 介绍 Attachment 插件是 Elasticsearch 中的一种插件,允许将各种二进制文件(如PDF、Word文档等)以及它们的内容索引到 Elasticsearch 中。插件使用 Apache Tika 库来解析和提取二进制文件的内容。通过使用 Attachment 插件&a…...
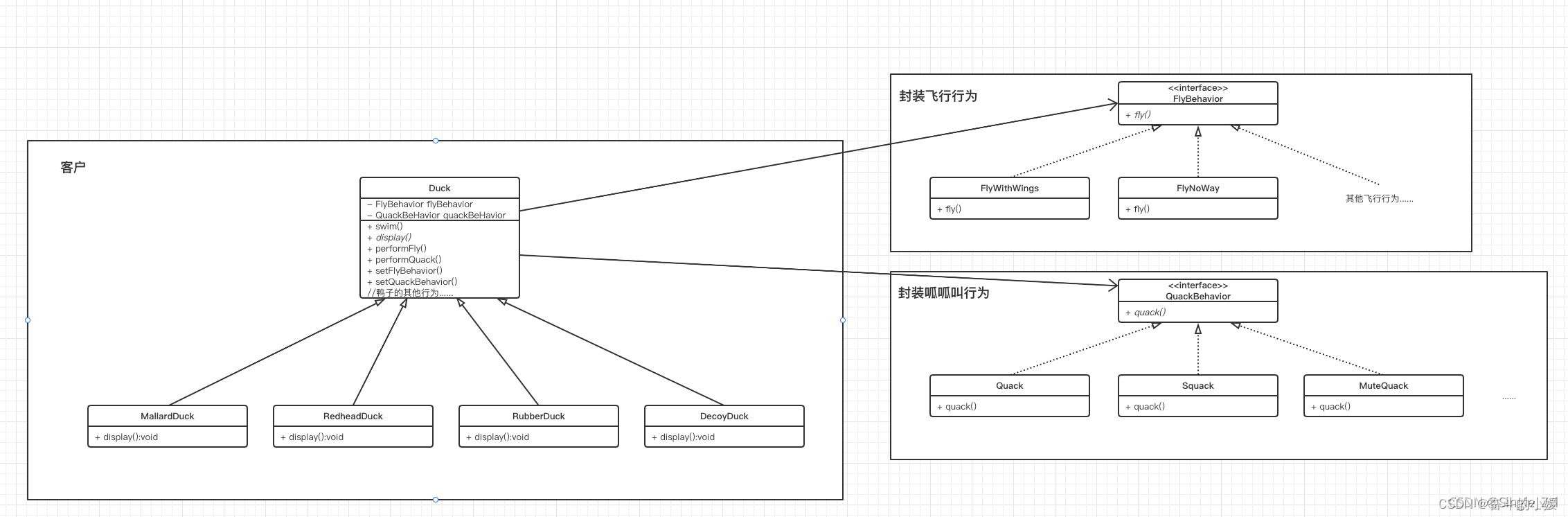
【Head First 设计模式】-- 策略模式
一、背景 Head First 设计模式第一章设计模式入门–策略模式 二、工具箱的工具(本章) 1、OO基础 封装 继承 多态 抽象 2、OO原则 封装变化 面向接口编程,而非面向实现编程 组合优于继承 3、OO模式 策略模式,所谓策略模式就是定义…...

能链智电,“重”症在身
文 | 智能相对论 作者 | 陈选滨 在过去的1-9月,充电基础设施增量为243.2万台,新能源汽车销量627.8万辆,充电桩与新能源汽车的增量比为1:2.6,距离工信部此前提出“2025年实现车桩比2:1,2030年实现车桩比1:…...
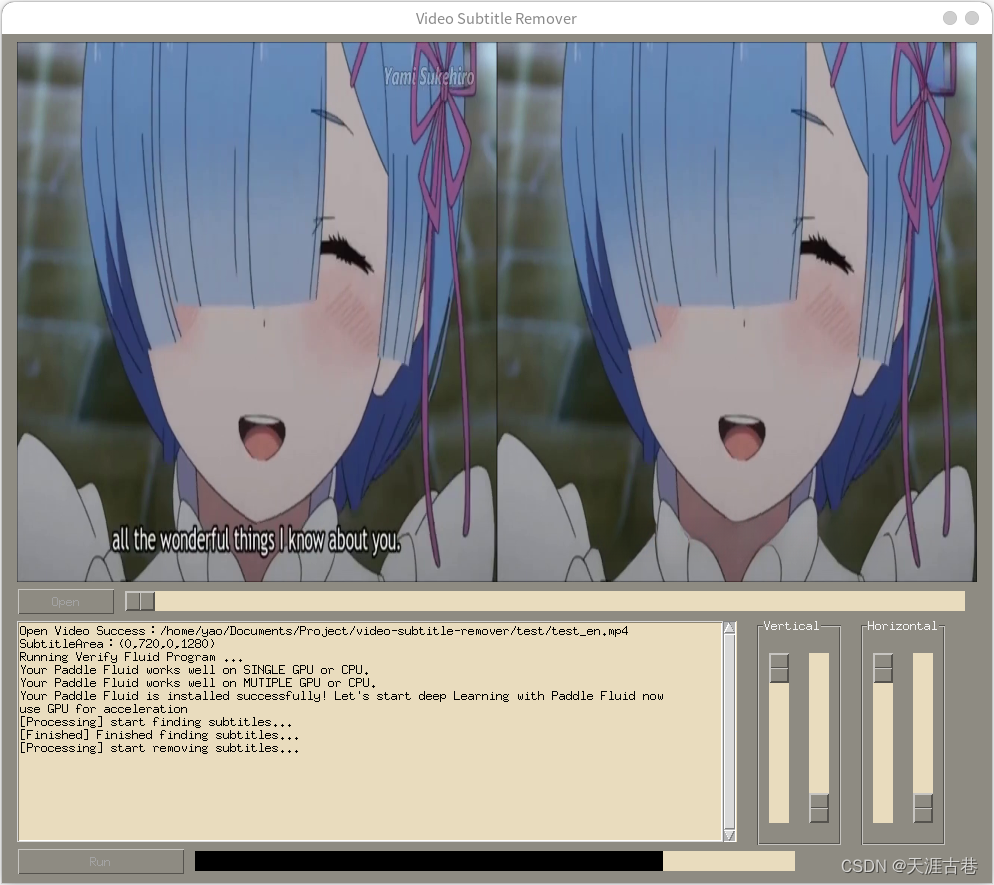
python 视频硬字幕去除 内嵌字幕去除工具 vsr
项目简介 开源地址:https://github.com/YaoFANGUK/video-subtitle-remover Video-subtitle-remover (VSR) 是一款基于AI技术,将视频中的硬字幕去除的软件。 主要实现了以下功能: 无损分辨率将视频中的硬字幕去除,生成去除字幕后…...
蓝桥等考C++组别六级004
第一部分:选择题 1、C L6 (15分) 关于switch语句,以下说法正确的是( )。 A. break语句只能用于switch语句。 B. switch语句中可以使用多个default语句。 C. switch语句中只能使用一个break语句。 D. …...

SpringBoot之Swagger
文章目录 前言一、Swagger简介二、SpringBoot集成Swagger三、配置Swagger四、配置扫描接口五、配置Swagger开关六、配置API分组七、实体配置八、常用注解 前言 作为后端开放人员,最烦的事就是自己写接口文档和别人没有写接口文档,不管是前端还是后端开发…...

抖音小店新的流量变现新时代!
随着短视频平台的日益崛起,抖音小店已成为电商领域的一股不可忽视的力量。抖音小店不仅具有极高的流量优势,还为众多商家提供了一个全新的销售渠道。那么,如何才能充分利用抖音小店的优势,打造出爆款商品,实现流量变现…...

软件架构师
软件架构师在软件开发过程中扮演着至关重要的角色,其主要职责包括: 需求分析:与用户和开发团队沟通,确定软件的需求和功能。设计架构:根据需求分析,设计软件的架构,包括系统架构、数据库架构、…...
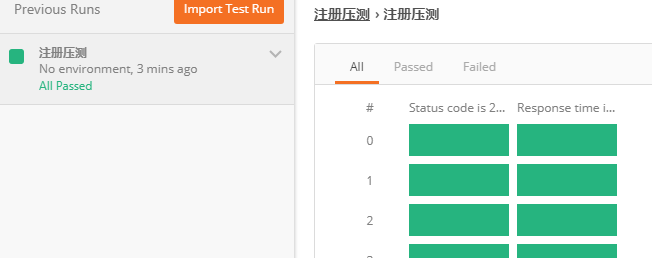
postman接口测试
postman使用 开发中经常用postman来测试接口,一个简单的注册接口用postman测试: 接口正常工作只是最基本的要求,经常要评估接口性能,进行压力测试。 postman进行简单压力测试 下面是压测数据源,支持json和csv两个格式…...

技术分享 | web自动化测试-PageObject 设计模式
为 UI 页面写测试用例时(比如 web 页面,移动端页面),测试用例会存在大量元素和操作细节。当 UI 变化时,测试用例也要跟着变化, PageObject 很好的解决了这个问题。 使用 UI 自动化测试工具时(包…...

Mall4cloud 微服务商城系统 2.0 发布
导读现在 jdk17 和 spring boot 以及 spring cloud alibaba 2022 的第三方依赖已经趋于成熟,所以 mall4cloud 也一把梭哈做了升级嗷。 本次更新重点: 系统由 jdk8 最低要求升级到 jdk17spring boot 由 2.7.x 升级到 3.1.xjavax 升级到 jakartaspring-cl…...
SpringBoot进制转换规则问题
1.填写yml文件 dataSource:driver-class-name: com.mysql.jdbc.Driver789password: 01272.测试类 package com.forever;import org.junit.jupiter.api.Test; import org.springframework.beans.factory.annotation.Value; import org.springframework.boot.test.context.Spri…...
12.输入一个小于1000的整数,输出平方根(不是整数,输出整数部分)
#include<stdio.h> #include<math.h>int fun(int n){int b;b pow(n,0.5);printf("%d",b);}int main(){int n;scanf("%d",&n); fun(n);return 0;}...

Django框架的推导
文章目录 Web应用简介什么是Web框架?什么是Web?应用程序的两种模式Web应用程序的优缺点 手写Web框架HTTP协议的相关知识1.四大特性2.请求数据格式3.响应数据格式 手写框架 使用wsgiref模块基于wsgiref模块搭建Web框架(最初版)基于wsgiref模块搭建Web框架…...

广东开放大学:电大搜题助力学子迎考利器
近年来,广东开放大学一直致力于为广大学子提供优质的教育资源和学习服务。作为一所专注于远程教育的学府,广东开放大学不仅拥有雄厚的师资力量和丰富的教育经验,还致力于创新教学手段,为学生提供更便捷、高效的学习体验。在这个信…...

linux 7za 编译安装
本文主要介绍了在linux下安装7z命令的方法,同时介绍了7z命令的使用。7z压缩格式拥有众多优点,具有极高的压缩比率 wget https://zenlayer.dl.sourceforge.net/project/p7zip/p7zip/16.02/p7zip_16.02_src_all.tar.bz2 tar -xjvf p7zip_16.02_src_all.ta…...
)
【Edge】微软Edge每次启动自动导入Chrome收藏夹,无法取消“每次启动浏览器时导入浏览数据”功能的解决方法(202311)
写在前面 Edge现在也不管用户体验了吗? 这个BUG都快一个月了,还没见修复,从118.0.2088开始,我是在2023年10月份一次更新后发现的这个BUG,结果社区论坛什么信息都没有,英文也没收到。 Edge的BUG现象 不知道哪次Edge…...

报错RuntimeError: no valid convolution algorithms available in CuDNN
报错信息如下RuntimeError: no valid convolution algorithms available in CuDNN 出现这个问题既不是cuda与cudnn版本不匹配,也不是英伟达显卡驱动需要更新!而是因为你的显存过低不能训练,解决办法是使用混精度训练!!…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
